【生存時間分析による離反時期分析 その3】
Python の生存時間分析ライブラリー Lifelinesで予測した
「離反時期（顧客であるまでの期間）」の精度検証

6002
【生存時間分析による離反時期分析 その3】Python の生存時間分析ライブラリー Lifelinesで予測した「離反時期（顧客であるまでの期間）」の精度検証

生存時間分析とは……

  • 生物の死
  • 顧客の離反
  • 機械システムの故障

……など、あるイベント（例：死、離反、故障など）が発生するまでの時間（期間）を推測するための統計学的なデータサイエンス技術です。

ここでは、顧客の離反までの時間（期間）の事例を扱います。

この記事は、以下の記事の続きになります。

【生存時間分析による離反時期分析 その2】
Python の生存時間分析ライブラリー Lifelines で実施する
「離反時期（顧客であるまでの期間）分析」

 

上記の記事は、ある通信会社の顧客の離反データ（Kaggleのサンプルデータ）を使い、Cox比例ハザードモデルの構築と、まだ離反していない継続顧客の離反時期予測を行いました。離反時期の予測は、生存関数（顧客である確率）を用いて行います。

予測値として例えば中央値を用いたりすることもありますが、予測結果は顧客ごとに関数（生存関数）として出力されます。1週間後に20%離反し、2週間後に50%離反し、3週間後に70%離反し、みたいな感じで出力されます。中央値とは50%離反するタイミングですので、この例では2週間後となります。

このような、関数として出力される予測結果に対し、どのように精度検証すればいいのでしょうか？

通常の機械学習系のモデルですと、学習データとテストデータにデータセットを分割し、学習データでモデルを構築し、テストデータでそのモデルを使って精度検証したりします。

今回は、前回の離反時期予測の事例を使って、生存関数の予測精度検証方法について説明します。

精度指標

生存時間分析ならではの精度指標があります。C-index（Concordance index、C統計量）と呼ばれるものです。

C-indexは、0～1の間の値を取り、値は大きいほうが良い

計算方法に付いては詳しく説明しませんが、それほど難しいものではありません。イメージだけお伝えします。

C-Indexは、生存時間の予測と実測の大小関係がどの程度一致しているかを表した指標です。大小関係の判定方法は、一般化Wilcoxon検定と同じです。

ちなみに、一般化Wilcoxon検定は、2群の生存時間に差があるかを検定する、ノンパラメトリック検定手法の1つです。似たようなものに、ログランク検定というのもあります。一般化Wilcoxon検定とログランク検定の違いは、一般化Wilcoxon検定が初期に起きたイベント（離反）を重く評価するのに対し、ログランク検定は後期に起きたイベント（離反）を重く評価する、というものがあります。

さらにさらに、Cox比例ハザードモデルを構築したとき、C-Indexと共にAICなどの情報量基準も出力されます。モデルの当てはまりのよさを見るためのAICなどの情報基準は、モデル選択（変数選択など）で利用することができます、

なにはともあれ、テストデータを使って予測精度を検証するときに利用するのは、C-Indexです。

 

サンプルデータ

通信会社の顧客の離反データ（Kaggleのサンプルデータ）を使います。以下のKaggleのページからCSVファイルをダウンロードしてお使いください。

Telco Customer Churn

生存時間として「契約期間」（tenure）、イベント生起として「離反」（Churn）となります。変数 customerID は個人を識別するIDで、その他の変数は、特徴量（説明変数X）です。

  • tenure：契約期間（生存時間）
  • Churn：離反（イベント生起）

 

全体の流れ

通信会社の顧客の離反データを使った、離反時期（顧客であるまでの期間）予測モデルの構築と精度検証、離反時期予測までの流れです。

  1. 必要なライブラリーの読み込み
  2. データセットの読み込み
  3. 前処理
  4. データセットの分割（学習データとテストデータ）
  5. 学習データでモデル構築
  6. テストデータで精度検証
  7. 継続顧客の離反時期予測

「3. 前処理」の詳細な説明は、前回の記事を参考にしていただければと思います。

【生存時間分析による離反時期分析 その2】
Python の生存時間分析ライブラリー Lifelines で実施する
「離反時期（顧客であるまでの期間）分析」

 

では、分析を進めていきます。

 

1. 必要なライブラリーの読み込み

必要なライブラリーを読み込みます。

以下、コードです。

# 必要なライブラリーの読み込み
import pandas as pd 
import numpy as np
from lifelines import *
from lifelines.utils import median_survival_times
from lifelines.utils import concordance_index
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt 

# グラフのスタイル
plt.style.use('ggplot')

# グラフサイズ設定
plt.rcParams['figure.figsize'] = [12, 9]

 

生存時間分析ライブラリー Lifelines 以外は、よく使う一般的なPythonのライブラリーです。

 

2. データセットの読み込み

通信会社の顧客の離反データ（Kaggleのサンプルデータ）を読み込みます。

以下、コードです。

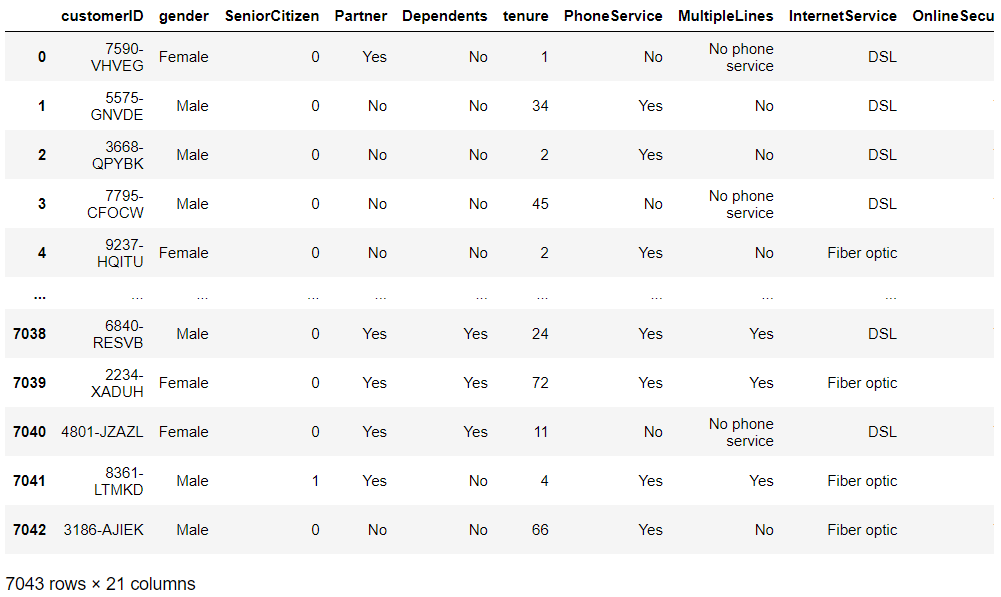
# データセットの読み込み
data_path = 'C:\dataset\WA_Fn-UseC_-Telco-Customer-Churn.csv'
df = pd.read_csv(data_path)
df #確認

 

以下、実行結果です。

 

PCのCドライブにあるフォルダ「dataset」に、「WA_Fn-UseC_-Telco-Customer-Churn.csv」というファイル名で格納した場合の例です。

 

3. 前処理

利用するデータセットの前処理をします。

どのような前処理をしているのかについては、前回の記事を参考にしてください。ここでは、まとめたコードでなっています。

以下、コードです。

# 前処理

## TotalCharges変数を型変換（数値型へ）
df.TotalCharges = pd.to_numeric(df.TotalCharges,
                                errors='coerce')

## 欠測値のある行を削除する
df = df.dropna(how='any')

## Churnの値変換（Yes:1、No:0）
df = df.replace({'Churn':{'Yes':1, 'No':0}})

## カテゴリカル変数のダーミ変数化（One Hot Encode）
df_dummy = pd.get_dummies(df.drop('customerID', axis=1),
                          drop_first=True)

## 上三角行列
arr = np.triu(abs(df_dummy.corr()), 1)
res = pd.DataFrame(np.where(arr, arr, np.nan),
                   index=df_dummy.corr().index,
                   columns=df_dummy.corr().columns)

# 縦持ちのデータに変換（相関係数の絶対値の高い順）
df_corr_melt = res.melt(ignore_index=False).dropna(how='any')

## 変数削除
del_col = df_corr_melt[df_corr_melt.value >= 0.99999].variable.unique()
df_dummy = df_dummy.drop(del_col, axis=1)

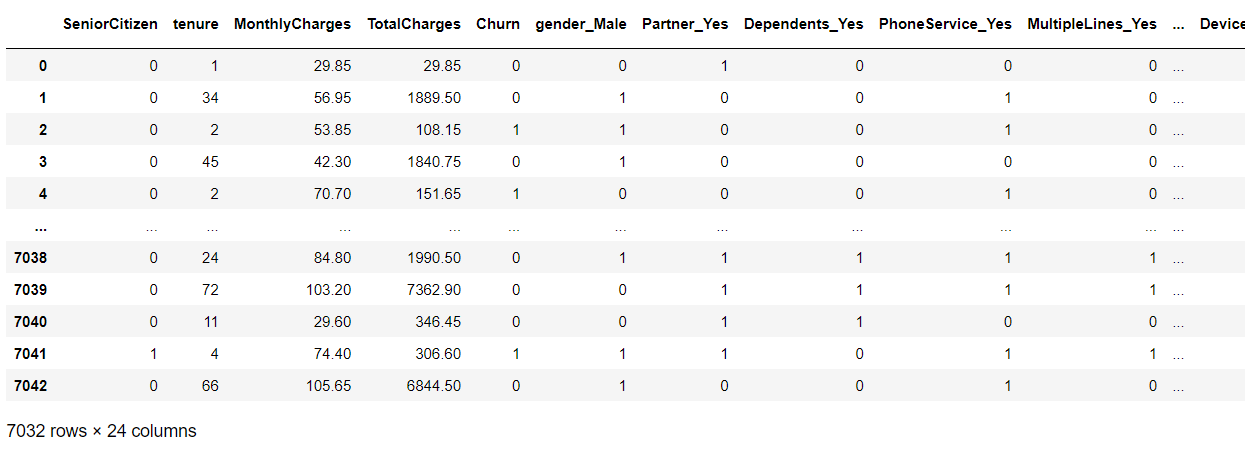
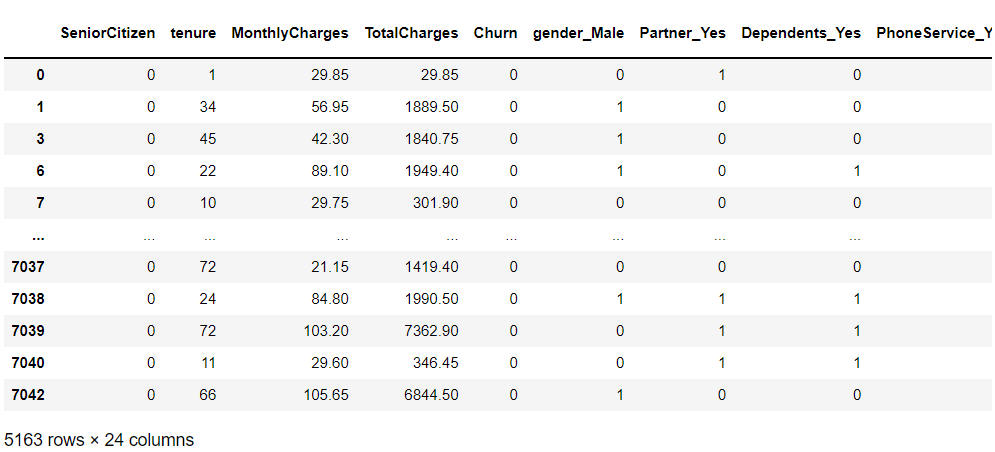
## 前処理後のデータセット
df_dummy

 

以下、実行結果です。

 

4. データセットの分割（学習データとテストデータ）

データセットを、学習データとテストデータの2つに分割します。学習データが70%で、テストデータが30％です。

以下、コードです。

# データセットの分割（学習データとテストデータ）
df_dummy_train, df_dummy_test = train_test_split(df_dummy,
                                                 test_size=0.3,
                                                 random_state=123
                                                )

 

  • df_dummy_train：学習データ　→　モデル構築
  • df_dummy_test：テストデータ　→　精度検証

 

5. 学習データでモデル構築

学習データ（df_dummy_train）を使って、Lasso（スパースモデリング）なCox比例ハザードモデル（Cox proportional hazard model）を構築します。

以下、コードです。

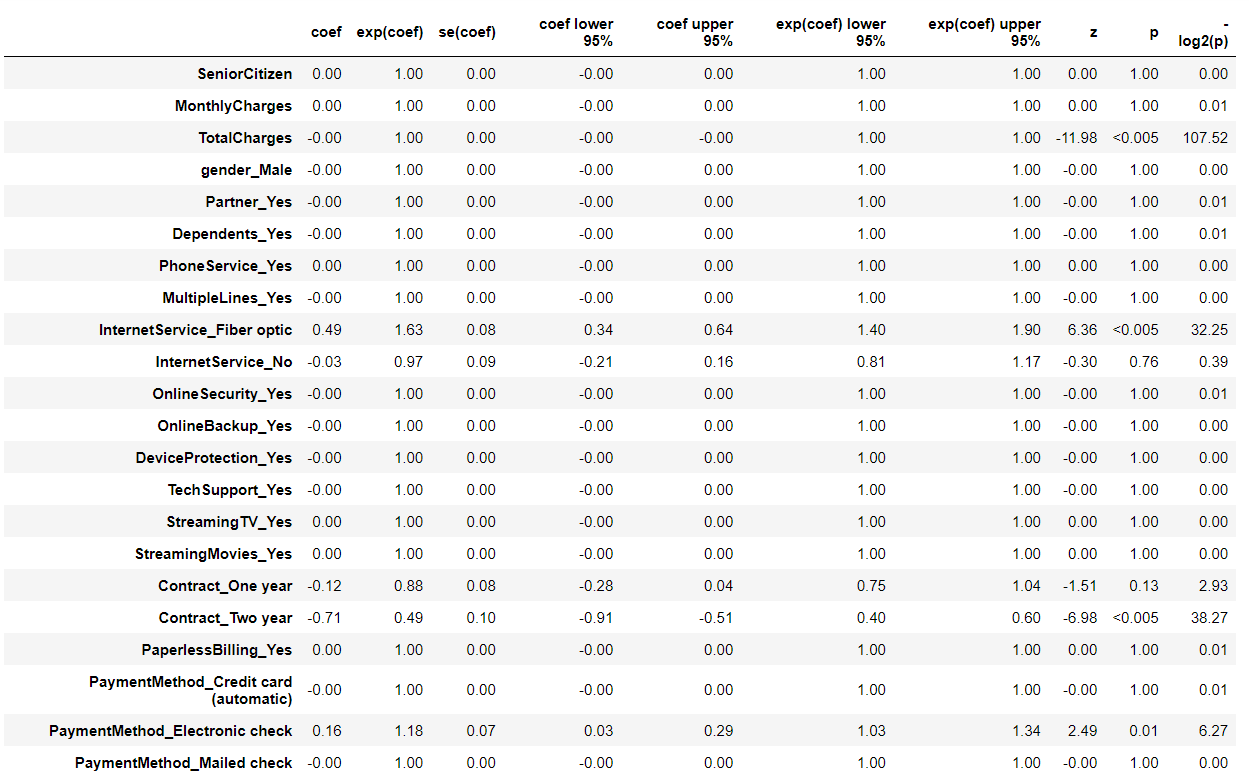
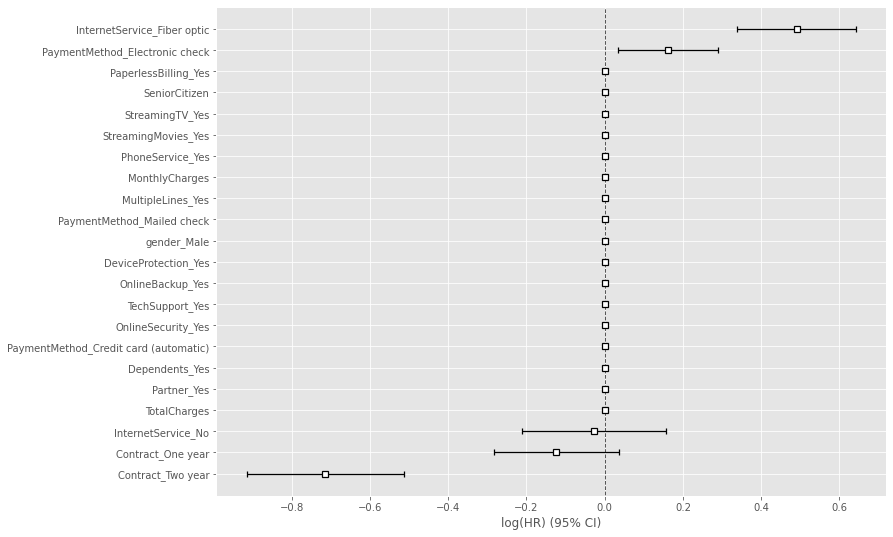
# 学習データを使いCox比例ハザード回帰（Lasso）モデルを構築
cph = CoxPHFitter(penalizer=0.1, l1_ratio=1)
cph.fit(df_dummy_train, duration_col='tenure', event_col='Churn') 

cph.print_summary() #サマリー
cph.plot() #係数

 

以下、実行結果です。

 

Concordanceという指標が出力されていますが、これがC-Indexです。学習データのC-Indexが0.92であることが分かります。

 

6. テストデータで精度検証

構築したモデルに対し、テストデータ（df_dummy_test）を使い精度検証します。端的に言うと、C-Indexを計算します。

Lifelinesライブラリーの中に、C-Indexを計算する関数があります。concordance_index()です。

試しに、学習データに対しC-Indexを計算してみます。

以下、コードです。

# 学習データで精度検証
## 学習データのC-Index（ハザード）
concordance_index(df_dummy_train['tenure'],
                  -cph.predict_partial_hazard(df_dummy_train),
                  df_dummy_train['Churn'])

 

以下、実行結果です。

 

C-Indexが0.9209925315330328であることが分かります。小数点第3位を四捨五入すると0.92です。モデル構築時に出力されたC-Indexの値と同じです（あたりまえですが……）。

 

この関数concordance_index()を使って、テストデータで構築したモデルの精度検証をします。

以下、コードです。

# テストデータで精度検証
## テストデータのC-Index（ハザード）
concordance_index(df_dummy_test['tenure'],
                  -cph.predict_partial_hazard(df_dummy_test),
                  df_dummy_test['Churn'])

 

以下、実行結果です。

 

C-Indexの値は、0.9220384377301543です。小数点第３位を四捨五入すると、0.92です。

学習データに対する精度と大差ありません。かなり予測精度のいいモデルであることが分かります。

 

先程、C-Indexは、生存時間の予測と実測の大小関係がどの程度一致しているかを表した指標だと説明しました。

予測モデルの精度検証と直接関係ないですが、大小関係が一致しているとはどういうことなのかを、グラフを描き説明します。

先ず、テストデータの顧客の生存関数を予測します。

以下、コードです。

# テストデータの生存関数
pred_survival = cph.predict_survival_function(df_dummy_test)

 

次に、離反した顧客のリストを出力します。

以下、コードです。

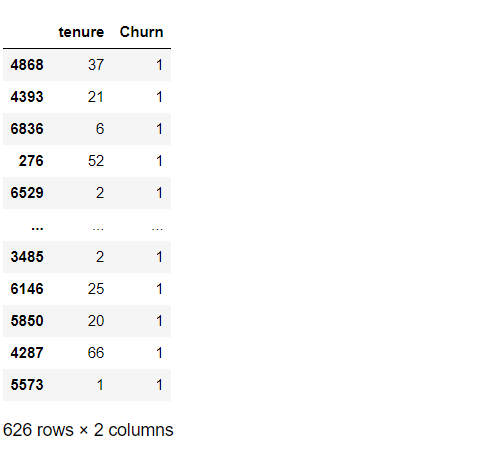
# 離反顧客の抽出
df_dummy_test[['tenure','Churn']][df_dummy_test['Churn'] == 1]

 

以下、実行結果です。

 

customer IDが4868と4393の生存関数をグラフで描写してみます。

ちなみに、「customer ID：4868」の「契約期間」（tenure）は「37」、「customer ID：4393」の「契約期間」（tenure）は「21」です。

「customer ID：4868」の方が「customer ID：4393」よりも「契約期間」（tenure）が長いです。要は、多くの時間で「customer ID：4868」の方が「customer ID：4393」よりも生存確率が高いはずです。

以下、コードです。

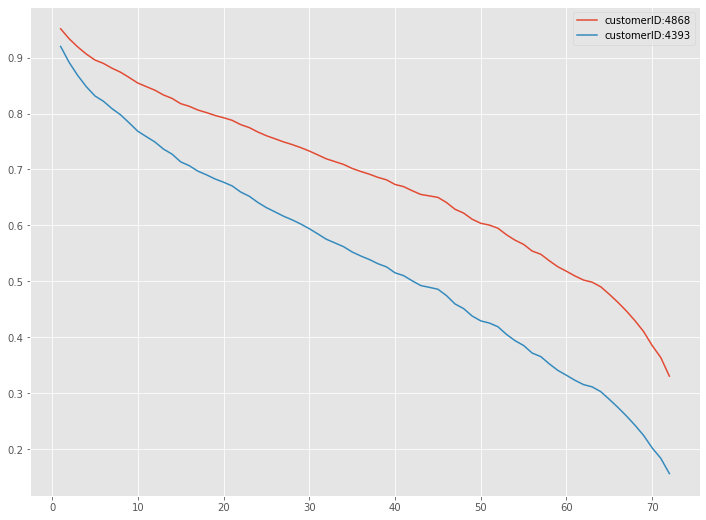
# テストデータの特定の顧客の生存関数のグラフ
customer1 = 4868
customer2 = 4393
pred_survival[customer1].plot(label="customerID:4868")
pred_survival[customer2].plot(label="customerID:4393")
plt.legend()

 

以下、実行結果です。

 

「customer ID：4868」の方が「customer ID：4393」よりも生存確率が高くなっていることが分かります。

「customer ID：4868」と「customer ID：4393」の場合、生存時間の予測と実測の大小関係が一致していることが分かります。

 

7. 継続顧客の離反時期予測

先程、学習データで構築したCox比例ハザード回帰モデルを、テストデータで精度検証しました。その結果、非常に良いことが分かりました。

そこで、全データセット（学習データとテストデータに分ける前のデータセット）を使い、Cox比例ハザード回帰モデルを構築し、まだ離反していない継続顧客の離反時期を予測をしてみたいと思います。

先ず、Cox比例ハザード回帰モデルを構築します。

以下、コードです。

# Cox比例ハザード回帰（Lasso）モデルを構築
cph = CoxPHFitter(penalizer=0.1, l1_ratio=1)
cph.fit(df_dummy, duration_col='tenure', event_col='Churn')

 

次に、まだ離反していない継続顧客を抽出します。

以下、コードです。

# 継続顧客（離反していない顧客）データの抽出
customers_data = df_dummy[df_dummy['Churn'] == 0]
customers_data #確認

 

以下、実行結果です。

 

抽出した継続顧客の生存関数を予測します。

以下、コードです。

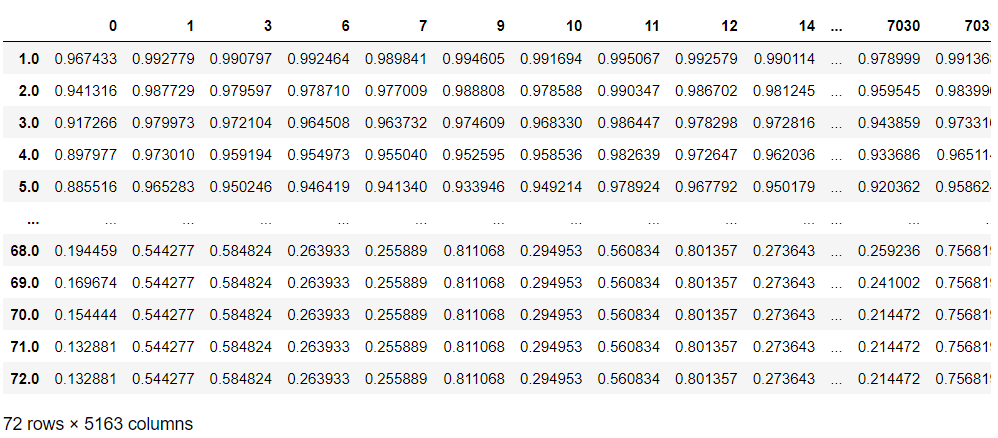
# 継続顧客の生存関数（打ち切り後の未来）
pred_survival_new_remain = cph.predict_survival_function(
    customers_data,
    conditional_after=customers_data['tenure']
)
pred_survival_new_remain #確認

 

以下、実行結果です。

 

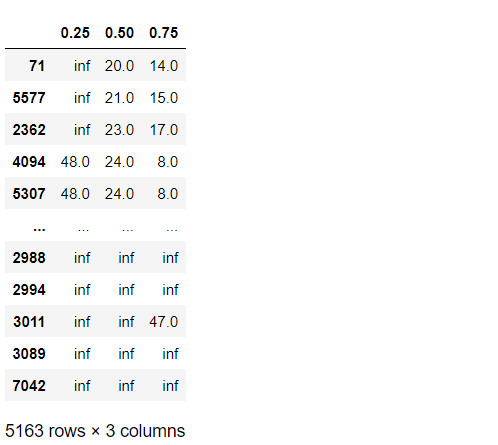
四分位を出力してみます。以下、コードです。

# 予測結果（第1四分位数，中央値（第2四分位数），第3四分位数）※離反しやすい順
cph.predict_percentile(
    customers_data,
    p=[0.25,0.50,0.75],
    conditional_after=customers_data['tenure']
).sort_values(0.50)

 

以下、実行結果です。

 

離反しやすい順に並び替えています。

このリストの上位順に、離反顧客対策を実施するといいでしょう。

 

まとめ

今回は、前回の離反時期予測の事例を使って、生存関数の予測精度検証方法について説明しました。

生存時間分析の精度検証方法は、機械学習の通常の分類問題と異なり、C-Indexを使います。

どうしても、機械学習の通常の分類問題と同様の精度指標で検証したいという方は、例えば、四分位の範囲内（第1四分位～第3四分位）の期間に離反したら正解、そうでなければ不正解とした正答率で考えてもいいでしょう。

ただ、四分位の範囲内（第1四分位～第3四分位）の期間を正解とした場合、不正解でも第1四半期より小さな時期と、第3四分位より大きな時期では、不正解の意味合いが異なりますので、注意しましょう。

【生存時間分析による離反時期分析 その1】離反時期の予測に使えるPython の生存時間分析ライブラリー Lifelines に慣れよう！

【生存時間分析による離反時期分析 その2】Python の生存時間分析ライブラリー Lifelines で実施する 「離反時期（顧客であるまでの期間）分析」