ビジネスの現場で目にする多くのデータは時系列データです。例えば、売上やセンサーデータなどです。
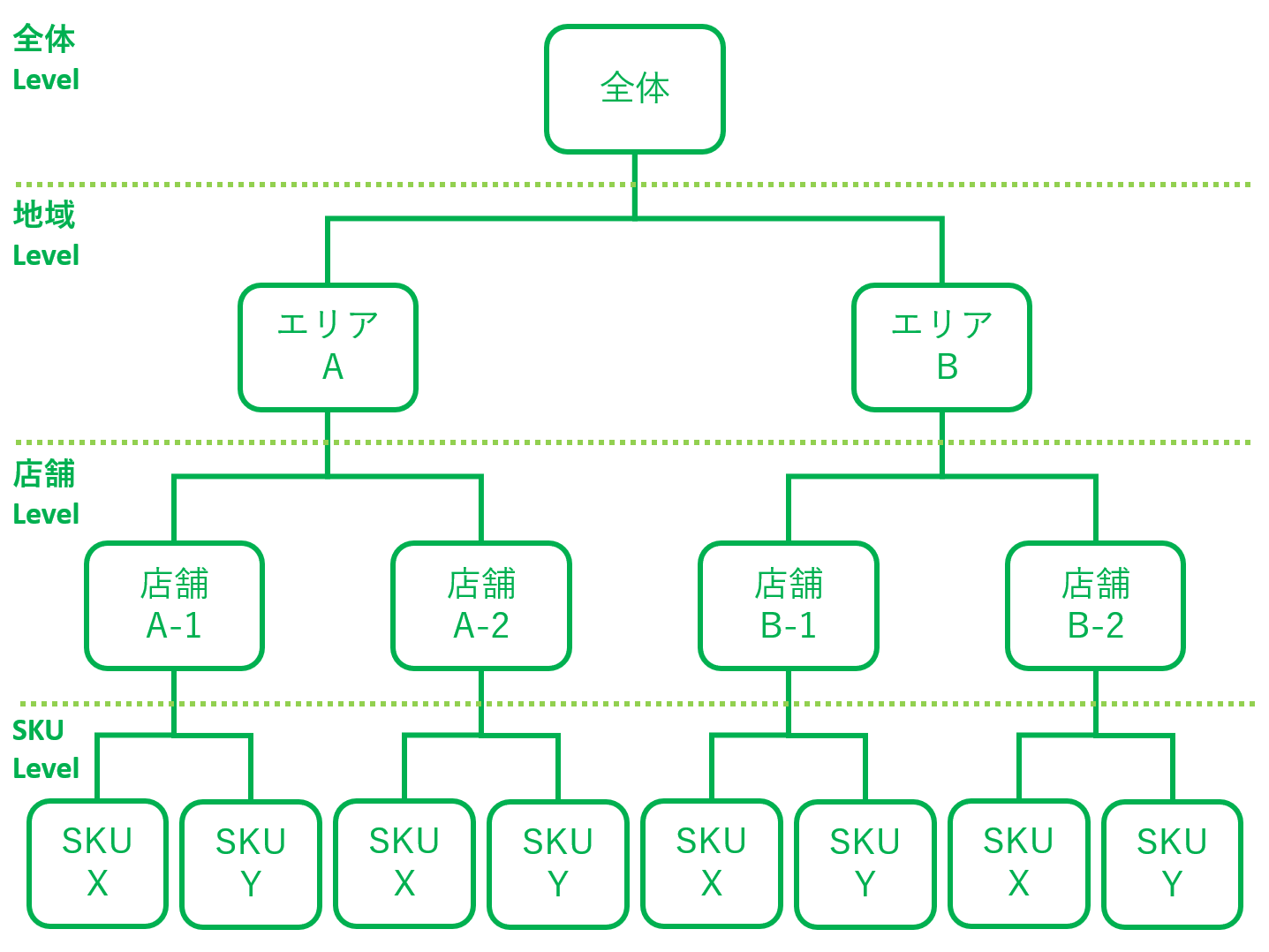
さらに、ビジネスの現場で目にする多くの時系列データは、階層構造を持っています。例えば、売上全体とエリアごとの売上、そのエリアの店舗ごとの売上、各店舗の商品(SKUなど)ごとの売上、などです。
このような階層時系列データは、どのように予測モデルを構築し、予測に活用すればいいのでしょうか。
今回は、「階層時系列データと予測モデル構築」というお話しをします。
Contents
4つの予測アプローチ
幾つかのアプローチ方法があります。
- ボトムアップアプローチ(bottom-up approach)
- トップダウンアプローチ(top-down approach)
- ミドルアウトアプローチ(middle-out approach)
- 最適調整アプローチ(optimal reconciliation approach)
それぞれについて、簡単に説明します。
ボトムアップアプローチ(bottom-up approach)
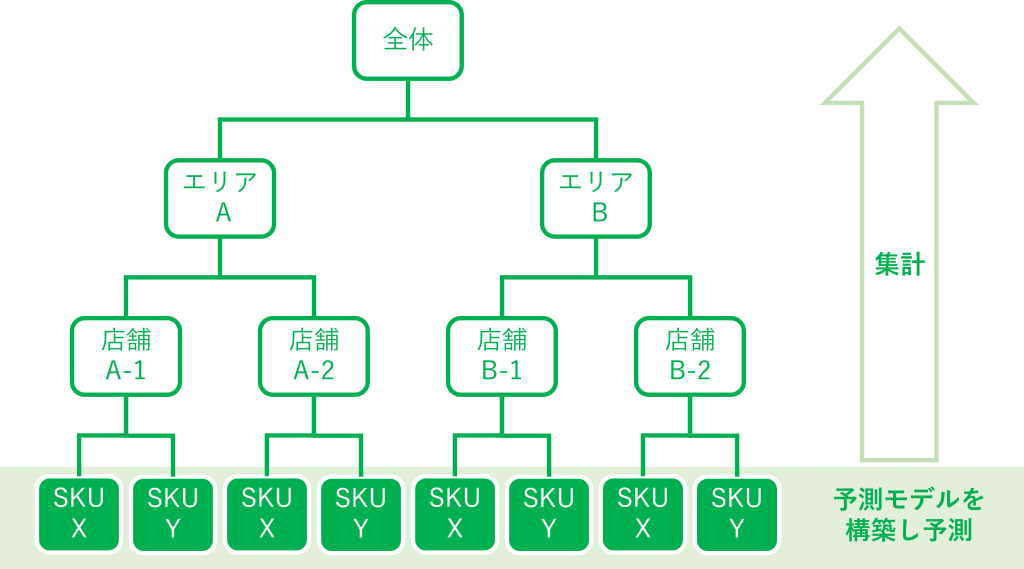
ボトムアップアプローチは、階層時系列予測で、最もよく使われる手法です。
階層の最下層の個々の時系列データに対し、予測モデルを構築します。予測結果は、最下層の時系列データに対しては予測モデルの予測値をそのまま利用し、上の層では下の層の予測値を合計したものを予測値として利用します。
ただ、最下層の時系列データに対する個々の時系列予測モデルの精度が悪い場合、それらを合計した上位層の時系列データの予測結果は、非常に悪くなる可能性があります。階層が深いほど悪くなります。場合によっては、最上位層(例えばその企業の売上全体など)の予測値が、目も当てられない感じになる場合もあります。
上位層の精度が悪くなるとは、上位層の時系列データに対し予測モデルを直接構築し予測した場合と比較したとき、下から足し上げた予測値の精度が非常に悪いということです。
そもそも、最下層の時系列データの値が非常に小さい数字(例:1個、2個、3個など)であったり、データの存在する期間が非常に短かったりと(例:今年の新商品のSKUなど)、非常に不安定な時系列予測モデルになることがあります。
トップダウンアプローチ(top-down approach)
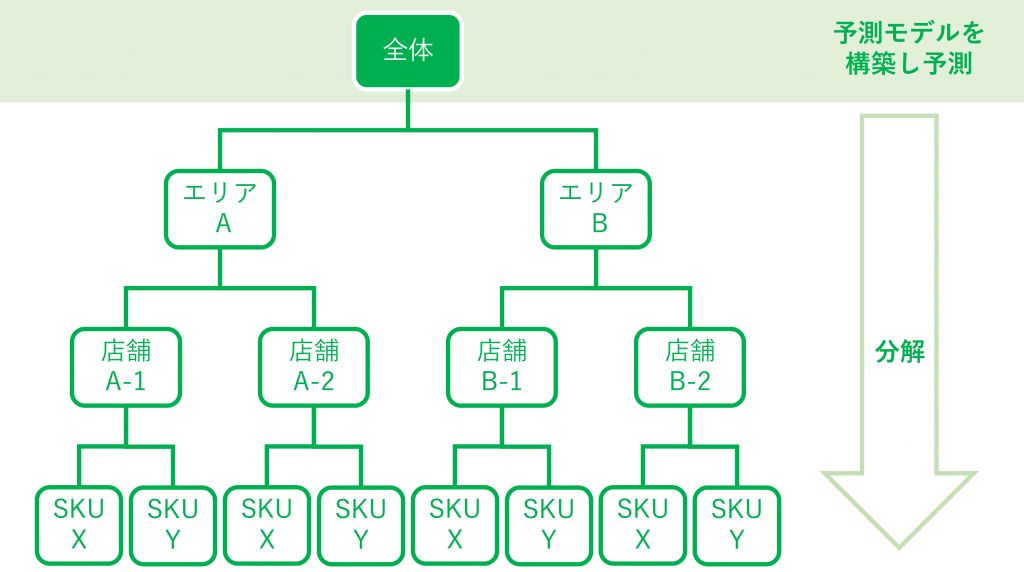
次に多いのがトップダウンアプローチです。
先ず「全体」(最上位層、例えばその企業の売上全体など)の予測モデルを構築し予測します。次に、予測結果を適切な割合に基づいて下の層に分解していきます。
当然ながら、最上位層など上の層ほど良い予測結果を出します。しかし、下の層に行くほど予測精度は悪化します。階層が深いほど悪くなります。
また、分割する割合に大きく依存するため、その割合をどう計算するのか、非常に大きな問題になります。
一番簡単なのは、最近の過去データから割合を導き出すことです。その場合、直近の予測値であればそれなりの結果になるかもしれませんが、遠い将来だと見当外れになります。
ミドルアウトアプローチ(middle-out approach)
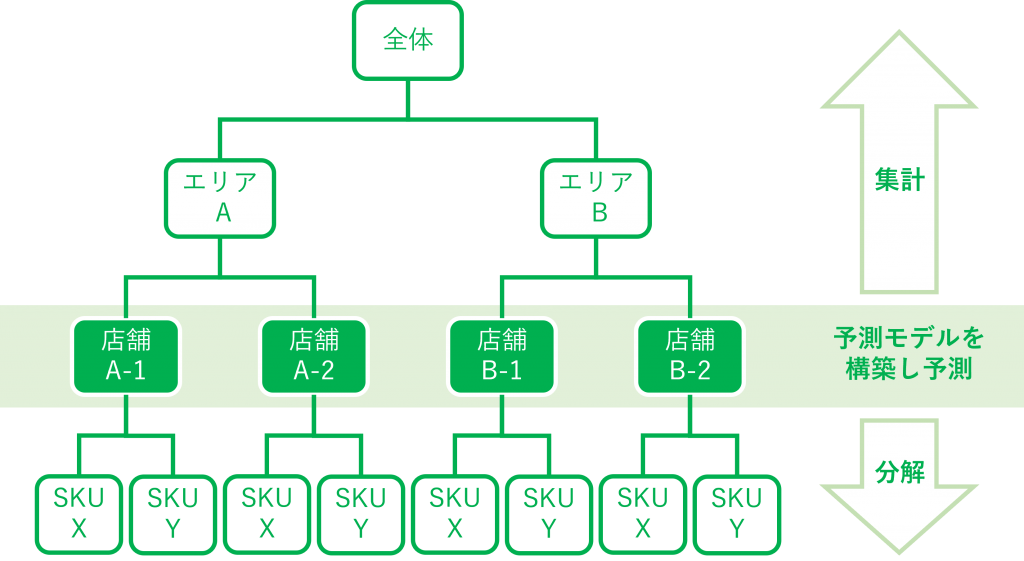
ボトムアップアプローチは、階層の下の層ほど良い予測結果を出します。トップダウンアプローチは、階層の上の層ほど良い予測結果を出します。
ミドルアウトアプローチは、ボトムアップアプローチとトップダウンアプローチを組み合わせたものです。
- 1.階層の中から予測モデルを構築し予測する中間レベルを選択
- 2.選んだ中間レベルの層のすべての時系列データ対し、予測モデルを構築し予測
- 3.ボトムアップアプローチとトップダウンアプローチを実施
- ミドルレベルよりも上の階層の時系列データ:ボトムアップアプローチで予測
- ミドルレベルよりも下の階層の時系列データ:トップダウンアプローチで予測
ここまでの3つの予測アプローチは、今からでもすぐできるようなものです。次に説明する最適調整アプローチは、ちょっと異なります。
最適調整アプローチ(optimal reconciliation approach)
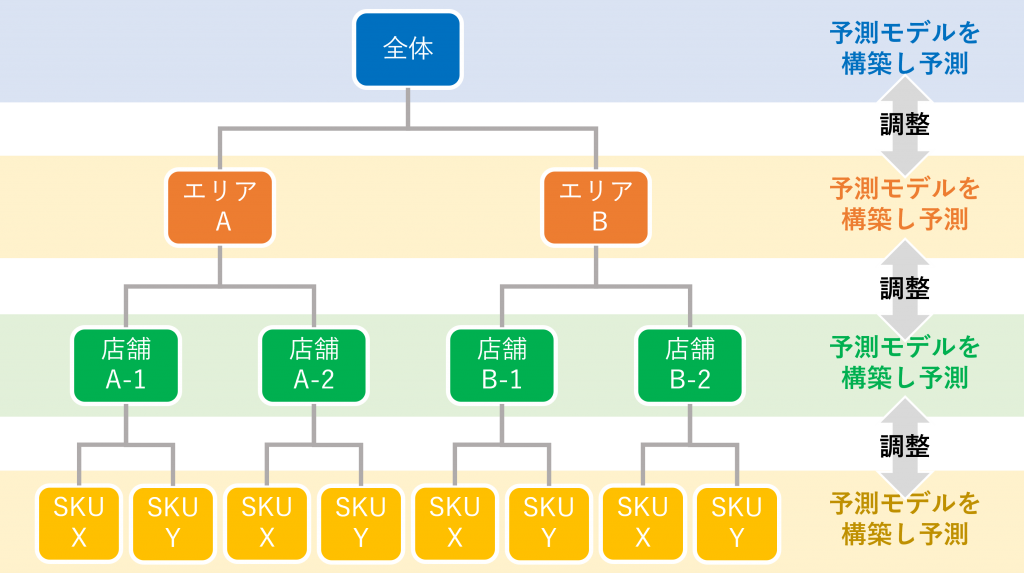
通常、予測モデルを構築し予測した層の予測結果は、良い予測精度になります。ボトムアップアプローチの場合は最下層、トップダウンアプローチの場合は最上位層、ミドルアウトアプローチの場合は選択した中間レベルの層の、時系列データです。
であれば、階層内のすべてのレベルの時系列データに対し予測モデルを構築し予測を実施すればいいのではないか、となりますが、そう単純でもありません。
個々の時系列データごとに予測モデルを構築し予測すると、下位層の予測値の合計が上位層の予測値になっている、という予測値の首尾一貫性は通常保たれません。
予測値の首尾一貫性を保つにどうすればいいのか、ということになり、そこで登場するのが最適調整アプローチです。
最適調整アプローチは、階層内のすべてのレベルの時系列データに対し予測モデルを構築し予測を実施し、その後、数理モデルの助けを借りてここの予測結果を調整し調整済み予測結果を計算します。
最適調整アプローチで利用する数理モデルは、最小2乗回帰(OLS:Ordinary Least Squares regression)を応用したものになります。要は、それほど難しいものではなく、非常にシンプルであるということです。
気になる方は、以下の論文などを一読してみてください。
Hyndman, RJ, Ahmed, RA, Athanasopoulos, G, and Shang, HL (2011)
https://robjhyndman.com/papers/Hierarchical6.pdfWickramasuriya, SL, Athanasopoulos, G & Hyndman, RJ (2019)
https://robjhyndman.com/papers/MinT.pdfSL Wickramasuriya et. al. (2019)
https://www.monash.edu/business/ebs/research/publications/ebs/wp15-2019.pdf
今回のまとめ
今回は、「階層時系列データと予測モデル構築」というお話しをしました。
ビジネスの現場で目にする多くのデータは時系列データです。例えば、売上やセンサーデータなどです。
さらに、ビジネスの現場で目にする多くの時系列データは、階層構造を持っています。例えば、売上全体とエリアごとの売上、そのエリアの店舗ごとの売上、各店舗の商品(SKUなど)ごとの売上、などです。
このような階層時系列データは、どのように予測モデルを構築し、予測に活用すればいいのでしょうか。
幾つかのアプローチ方法があります。
- ボトムアップアプローチ(bottom-up approach)
- トップダウンアプローチ(top-down approach)
- ミドルアウトアプローチ(middle-out approach)
- 最適調整アプローチ(optimal reconciliation approach)
すぐにできそうなものから、そうでないものまであります。最適調整アプローチ(optimal reconciliation approach)以外は、すぐにでもできるかと思います。
詳細を知りたい方や、実際にPCなどで予測モデルを構築して見たい方は、Rの有名な時系列パッケージforecast関連の資料を参考にして頂ければと思います。Rのforecast系の階層時系列用のパッケージhtsを使い簡単にモデル構築はできます。
Pythonで利用されたい方は、PythonからRのforecastを利用するか、scikit-htsというPythonの専用ライブラリーを利用するか、どちらかになります。ただ、scikit-htsがまだまだ改良の余地があるためお勧めできません。