Pythonの数値計算ライブラリーと言えば、NumPyやSciPyなどでしょう。
NumPyなどと異なり、数式そのものを記述するスタイルを取るライブラリーもあります。Theanoです。

https://theano-pymc.readthedocs.io/en/latest/
数式で考えるクセのある数理系の人にとっては、Theanoの方が便利かもしれません。
そして、Theanoはディープラーニングを強く意識したライブラリーということもあり、ある程度使いこなせるようになると、そのあたりのモデリングも難なく実現できます。
ということで、今回は「Python用の数値計算ライブラリーTheano超々入門」というお話しです。
基礎のキソの基礎のキソの基礎、といったレベルのお話しです。
Theanoのインストール
Anaconda環境を前提にします。
コマンドプロンプトに、以下のコードを入力しインストールしてください。
conda install theano
Theanoのコード化と実行の3ステップ
Theanoは、主に以下の3つのステップで動作します。
- ステップ1:数式の定義
- ステップ2:関数の生成(コンパイル)
- ステップ3:関数の利用
初めての人は意味不明だと思いますので、簡単な例で流れを説明します。
超簡単な数式の例
以下の関数を作り、作った関数に値を代入し使ってみます。
先ずは、必要なライブラリーを読み込みます。
以下、コードです。
# ライブラリーの読み込み import numpy as np import theano import theano.tensor as T from theano import function
ステップ1から3を順番に進めて行きます。
ステップ1の「数式の定義」です。
以下、コードです。
# ステップ1:数式の定義 ## 変数 x1 = T.scalar() x2 = T.scalar() x3 = T.scalar() ## 数式 y = x1 * x2 + x3
スカラーとベクトル、行列、テンソルなどを変数として指定できます。
ちなみに、Theanoの中では変数と呼ばずシンボルと呼びます。
今回は、スカラーを表すシンボルx1、x2、x3を宣言し、それを使い数式を定義しています。
ステップ2の「関数の生成(コンパイル)」です。
以下、コードです。
# ステップ2:関数の生成(コンパイル)
f1 = function(inputs=[x1, x2, x3],
outputs=y,
)
これで関数
ステップ3の「関数の利用」です。
以下、コードです。
# ステップ3:関数の利用 print(f1(1, 2, 3))
以下、実行結果です。
これは、
概ね雰囲気を掴めたかと思います。
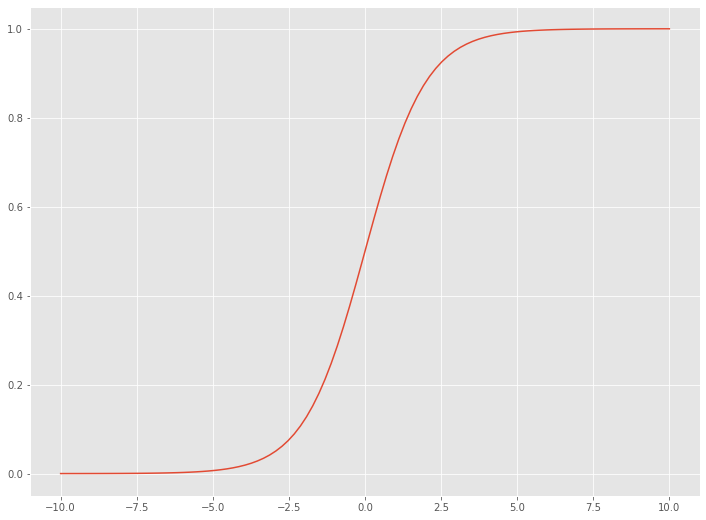
簡単なシグモイド関数の例
以下のような数式を作り、使ってみたいと思います。
先ずは、必要なライブラリーを読み込みます。
以下、コードです。
# ライブラリーの読み込み
import numpy as np
import theano
import theano.tensor as T
from theano import function
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ
ステップ1から3を順番に進めて行きます。
ステップ1の「数式の定義」です。
以下、コードです。
# ステップ1:数式の定義 ## 変数 x = T.scalar() ## 数式 y = 1/(1 + T.exp(-x))
ステップ2の「関数の生成(コンパイル)」です。
以下、コードです。
# ステップ2:関数の生成(コンパイル)
f2 = function(inputs=[x],
outputs=y,
)
ステップ3の「関数の利用」です。
以下、コードです。
# ステップ3:関数の利用
## xの値
xs = np.linspace(-10,10,100)
## yの値
ys = []
for x_i in xs:
ys.append(f2(x_i))
## グラフ化
plt.plot(xs,ys)
plt.show()
以下、実行結果です。
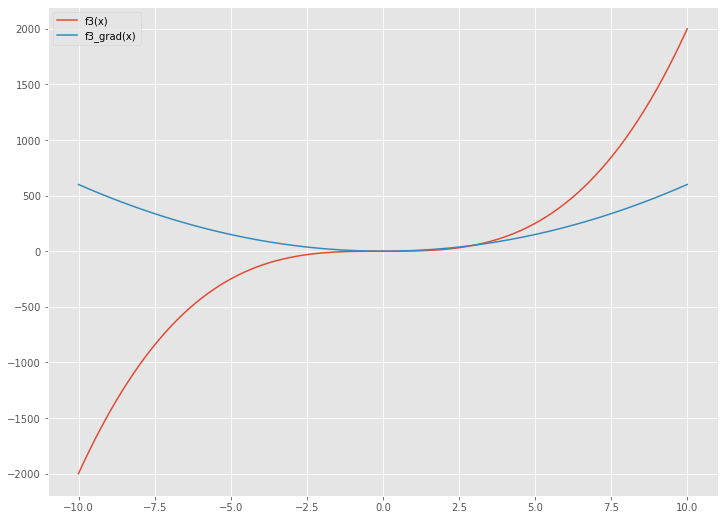
簡単な関数と導関数(1階微分)の例
以下のような数式を作り、さらに
先ずは、必要なライブラリーを読み込みます。
以下、コードです。
# ライブラリーの読み込み import numpy as np import theano import theano.tensor as T from theano import function
ステップ1から3を順番に進めて行きます。
ステップ1の「数式の定義」です。
以下、コードです。
# ステップ1:数式の定義
## 変数
x = T.scalar()
## 数式
y = 2*(x**3)
z = T.grad(cost=y, #微分する対象
wrt=x #微分を取る変数
)
ステップ2の「関数の生成(コンパイル)」です。
以下、コードです。
# ステップ2:関数の生成(コンパイル)
f3 = function(inputs=[x],
outputs=y,
)
f3_grad = function(inputs=[x],
outputs=z,
)
ステップ3の「関数の利用」です。
今作成した関数と導関数に値を代入してみます。
以下、コードです。
# ステップ3:関数の利用その1
print('f3(1) =',f3(1))
print('f3_grad(1) =',f3_grad(1))
以下、実行結果です。
これは、
今作成した関数と導関数をグラフで見てみます。
以下、コードです。
# ステップ3:関数の利用その2
## xの値
xs = np.linspace(-10,10,100)
## yの値
### f3
f3_ys = []
for x_i in xs:
f3_ys.append(f3(x_i))
### f3_grad
f3_grad_ys = []
for x_i in xs:
f3_grad_ys.append(f3_grad(x_i))
## グラフ化
plt.plot(xs,f3_ys,label='f3(x)')
plt.plot(xs,f3_grad_ys,label='f3_grad(x)')
plt.legend()
plt.show()
以下、実行結果です。
まとめ
今回は「Python用の数値計算ライブラリーTheano超々入門」というお話しをしました。
なんとなく、どのようなものかイメージが付いたかと思います。Theanoは、ベイズモデリングやディーラーニングなどで利用できます。別の機会に取り上げたいと思います。
また、Theanoの後継としてAesaraというライブラリーが開発されています。こちらも、別の機会にお話しします。
https://aesara.readthedocs.io/en/latest/
基本的なところはほぼ同じように感じられますが、微妙に異なります(互換性という意味において……)。