実践的なデータサイエンスで、ちょくちょく出てくる確率分布が、二項分布とベータ分布です。
二項分布(Binomial Distribution)は、「成功率」の分かっている試行をn回行ったときの「成功回数」を確率変数とする離散確率分布です。
例えば、表のでる確率が0.5のコインを10回投げたとき、「表がx回でる確率」を求めます。
ベータ分布(Beta Distribution)は、「成功回数」と「失敗回数」が分かっているときの「成功率」を確率変数とする連続値型確率分布です。
例えば、コイン投げを10回し表が4回、裏が6回でたときの「表のでる確率p」を求めます。
二項分布とベータ分布は、仲が良さそうですね。
今回は、「Pythonで描く二項分布とベータ分布」というお話しをします。
Contents [hide]
Pythonで描く二項分布
非常に馴染みのある確率分布の1つが、二項分布です。高校などで学ぶのではないでしょうか。
成功確率pのベルヌーイ試行をn回行ったとき、ある事象が何回起こるかを表現します。ベルヌーイ試行とは、結果が2通り(例:成功 or 失敗、受注 or 失注う、継続 or 離反、など)しかない試行をさします。
成功確率pの二項分布の確率質量関数は、以下のように表現されます。
- 期待値:
- 分散:
Pythonで二項分布を描いてみます。SciPyを使います。10回試行、成功確率0.2の二項分布です。
以下、コードです。
# 二項分布
## ライブラリー読み込み
from scipy.stats import binom
import matplotlib.pyplot as plt
## グラフの表示設定
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ
## 計算
n = 10 #試行回数
p = 0.2 #成功確率
x = range(n) #x軸
f = binom(n, p) #確率分布
y = f.pmf(x) #y軸
## グラフ
plt.bar(x, y)
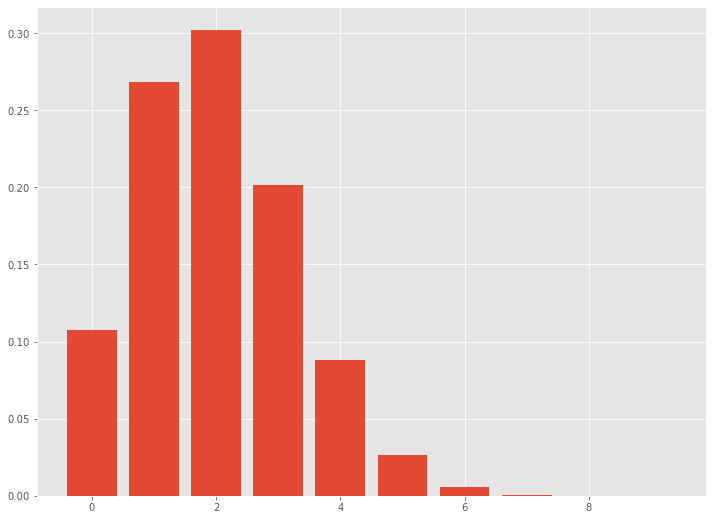
以下、実行結果です。
10回試行、成功確率0.2の二項分布です。
以下、コードです。
## 計算 n = 100 #試行回数 p = 0.2 #成功確率 x = range(n) #x軸 f = binom(n, p) #確率分布 y = f.pmf(x) #y軸 ## グラフ plt.bar(x, y)
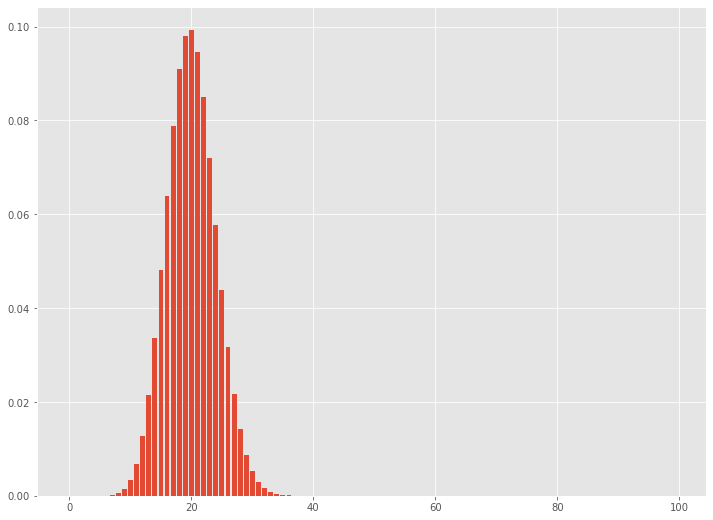
以下、実行結果です。
正規分布
以下、コードです。
from scipy.stats import norm import math x = range(n) #x軸 y = norm.pdf(x, n * p, math.sqrt(n * p * (1-p))) plt.bar(x, y)
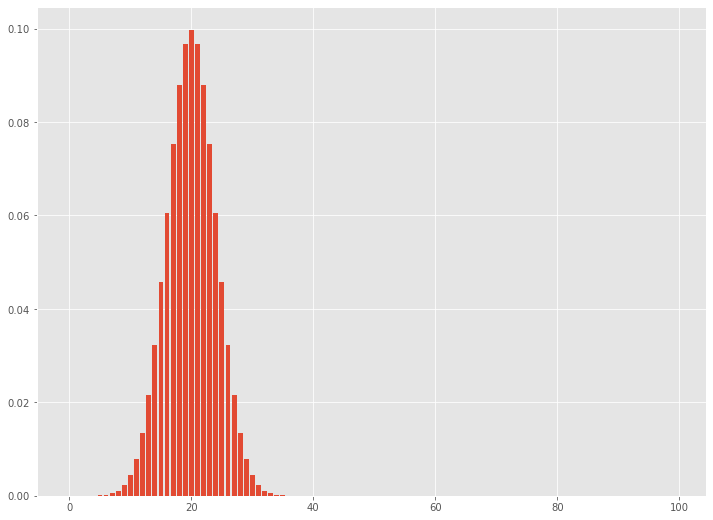
以下、実行結果です。
正規分布と近似していることが分かると思います。
Pythonで描くベータ分布
ベータ分布は、二項分布ほど馴染みはないでしょう。ただ、人によっては、高校などで学んでいる方もいることでしょう。
成功回数m=α-1、失敗回数n=β-1のベータ分布の確率密度関数は、以下のように表現されます。
- 期待値:
- 最頻値・中央値:
- 分散:
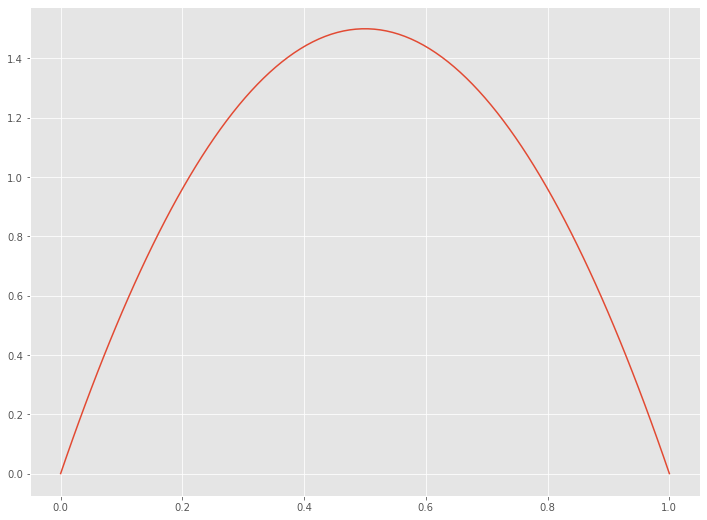
Pythonでベータ分布を描いてみます。SciPyを使います。α=2、β=2のベータ分布です。
以下、コードです。
# ベータ分布
## ライブラリー読み込み
from scipy.stats import beta
import numpy as np
import matplotlib.pyplot as plt
## グラフの表示設定
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ
## 計算
a = 2
b = 2
x = np.linspace(0, 1, 100) #x軸
y = beta.pdf(x, a, b) #y軸
## グラフ
plt.plot(x, y)
以下、実行結果です。
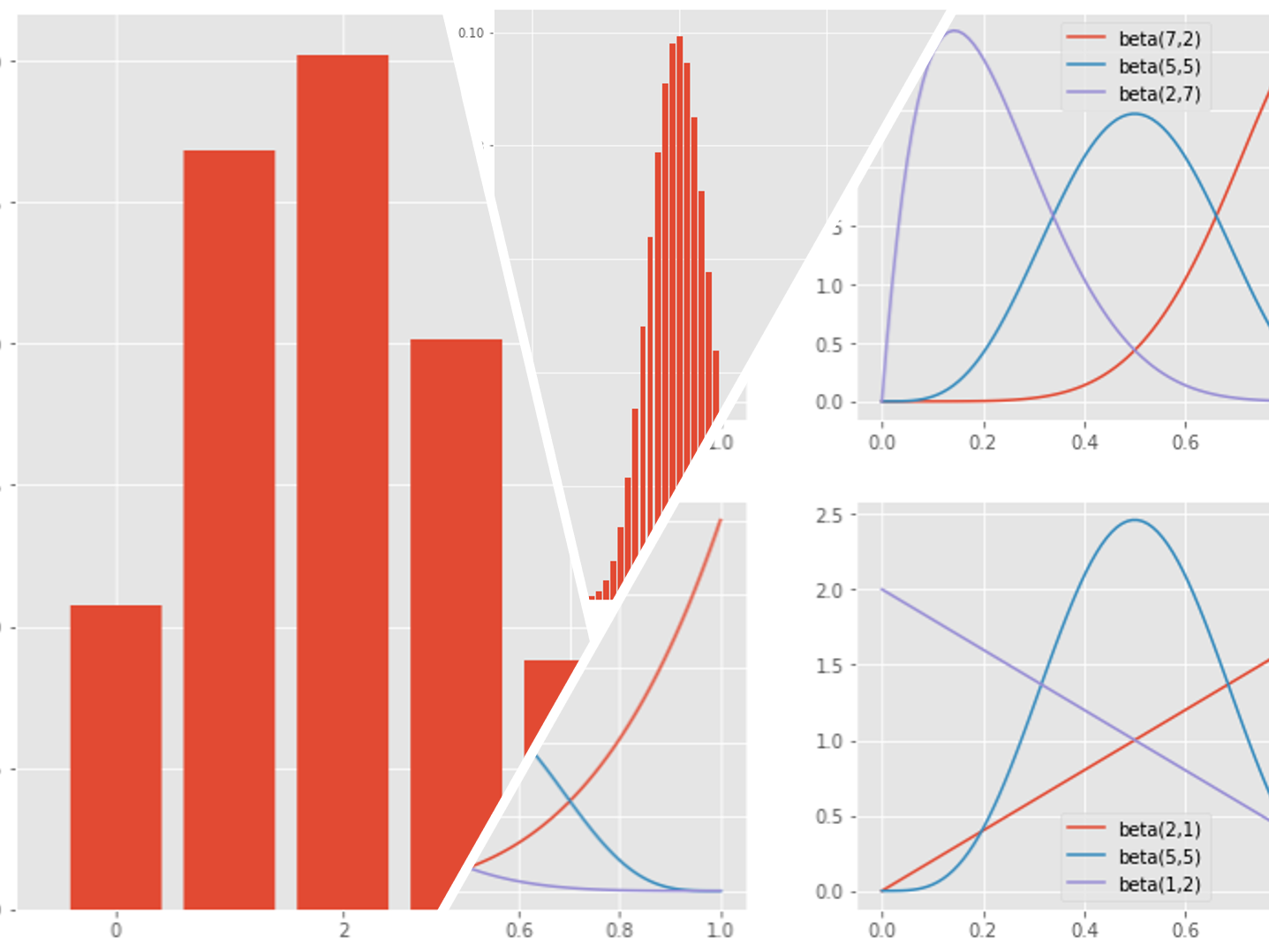
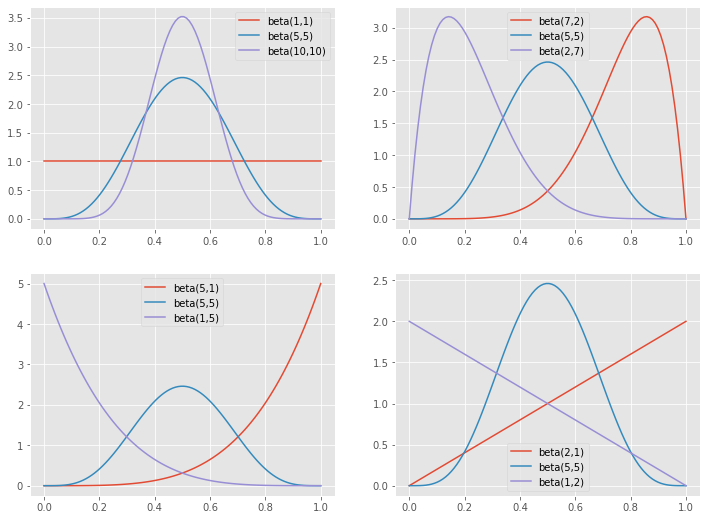
ベータ分布は、αとβの値によって、色々な形状の分布を描けます。色々変えてみます。
以下、コードです。
# x軸 x = np.linspace(0, 1, 100) # グラフ1 plt.subplot(2, 2, 1) plt.plot(x, beta.pdf(x, 1, 1), label='beta(1,1)') plt.plot(x, beta.pdf(x, 5, 5), label='beta(5,5)') plt.plot(x, beta.pdf(x, 10, 10), label='beta(10,10)') plt.legend() # グラフ2 plt.subplot(2, 2, 2) plt.plot(x, beta.pdf(x, 7, 2), label='beta(1,1)') plt.plot(x, beta.pdf(x, 5, 5), label='beta(5,5)') plt.plot(x, beta.pdf(x, 2, 7), label='beta(10,10)') plt.legend() # グラフ3 plt.subplot(2, 2, 3) plt.plot(x, beta.pdf(x, 5, 1), label='beta(1,1)') plt.plot(x, beta.pdf(x, 5, 5), label='beta(5,5)') plt.plot(x, beta.pdf(x, 1, 5), label='beta(10,10)') plt.legend() # グラフ4 plt.subplot(2, 2, 4) plt.plot(x, beta.pdf(x, 2, 1), label='beta(1,1)') plt.plot(x, beta.pdf(x, 5, 5), label='beta(5,5)') plt.plot(x, beta.pdf(x, 1, 2), label='beta(10,10)') plt.legend() # グラフ表示 plt.show()
以下、実行結果です。
まとめ
今回は、「Pythonで描く二項分布とベータ分布」というお話しをしました。
ベータ分布は使い勝手のいい確率分布で、特にベイズ統計の事前分布で重宝されています。