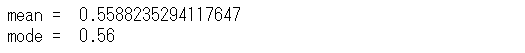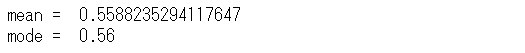需要予測などで、特定の値(予測値が1つ)だけではなく、予測値の区間や分布が手に入った方が嬉しい場合があります。
区間だけであれば、従来の推定方法(最尤法など)で求めることはできます。95%信頼区間(予測区間)などです。
もちろん、このような区間はベイズ推定でも求めることはできます。
知り得たいのが区間だけであれば、従来の推定方法だろうがベイズ推定であろうが、どちらでもいいかもしれません。
しかし、ベイズ推定の場合、区間以上の情報を得ることができます。
どのような情報かというと、分布です。
この分布から平均値や最頻値などを予測値やその区間などを求めることができます。
それだけではありません。
ベイズ推定の面白いところは、今手元にあるデータが多かろうが少なかろうが取り急ぎ分布などを計算し、新たなデータを手にしたときにその分布を更新していく、というアプローチを取ります。
更新前の分布を「事前分布」、更新後の分布を「事後分布」と言います。
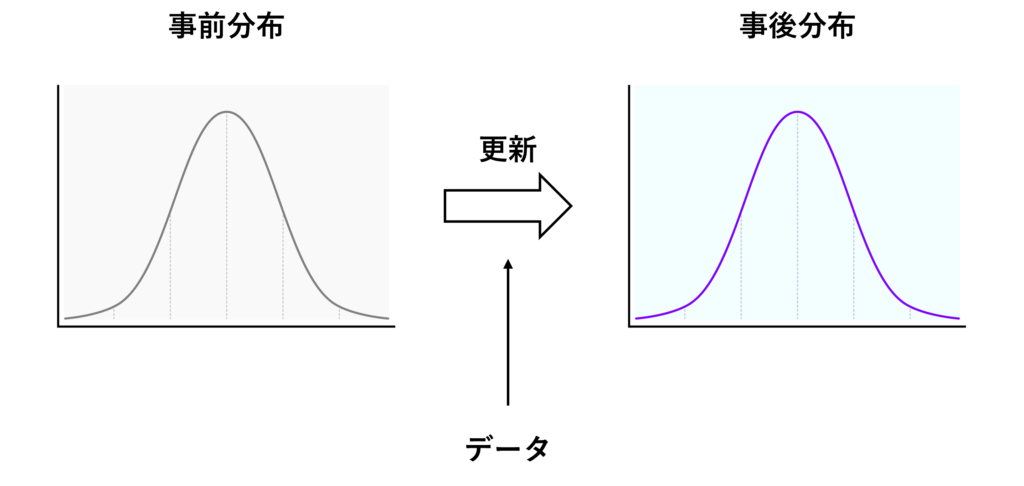
そこで問題になってくるのが、最初の事前分布です。
事前分布は経験値などをもとに主観的に設定するか、よく分からないという理由で無情報事前分布を設定する、というケースが多いです。
無情報分布とは、一様分布などです。よく利用されます。
ただ、推定するパラメータの種類によって無情報分布を変えるのが一般的です。
例えば、、、
- 正負の両方を取りうるパラメータのとき正規分布を利用したり、
- 分散などの正の値しかとらない場合はガンマ分布を使用したり、
、、、します。
この新たなデータを手にしたときに分布を更新していくというアプローチは、何かしら事前分布を設定することで、ちょっとしたいいことがあります。
それは、データ量が少ない場合でも、何かしら推定結果を得られることです。
「データが少ないので何も言えません」ではなく、「データが少ないなりにこういうことが言えました」という感じになるということです。

この話しをすると、決まって次のような心配の声がちょくちょくあがります。
「最初に設定した事前分布が的外れでも大丈夫? 」
データが増えれば増えるほど大丈夫になります。
なぜならば、何となく設定した事前分布も、データ量が増えるほど、実際のデータにより更新(学習)されていき修正され、最初の事前分布の影響が小さくなり、いい感じの事後分布に進化するからです。
この進化は、時代の変化に応じて事後分布が都度更新(学習)され方向修正されるということも意味しています。
すばらしい! ……となりますが、ここで非常に大きな問題が浮上します。
それは、事後分布はいつも簡単に計算できるわけではない、という厄介な問題です。

そこで、モンテカルロシミュレーションという乱数を活用した方法が利用されるようになりました。
最近では、マルコフ連鎖を利用したモンテカルロシミュレーションであるMCMC(マルコフ連鎖モンテカルロシミュレーション)法を使うのが一般的です。
このMCMCを実施するときに使うPythonパッケージは多々あります。例えば、PyStanやPyMCなどです。
今回は、「コイン投げの例を使ってベイズ推定を何となく理解しよう」というお話しをします。今回は、PyMC3は登場しません。
コイン投げ

コイン投げの例で説明を進めていきます。
コインには表と裏があります。コインを投げると、表になったり裏になったりします。それを数字で記録していきます。
- 表:1
- 裏:0
そうすると、次のような0-1のデータが手に入ります。
0010010111011001010101011111000…00101110
100回コイン投げをしたとします。このとき……
- 表;56回
- 裏:44回
……でたとします。
このコインの表の出る確率は、どうでしょうか?
このデータがなければ、0.5と考えるかもしれません。このデータから、0.56(=56/100)と考えるかもしれません。
ベータ分布で考えてみよう
ここでは、以下のベータ分布を使います。
ベータ分布に関して知りたい、という方は以下の記事を参考にしてください。
Pythonで描く二項分布とベータ分布
ベータ分布のパラメータを以下のように設定します。
- α = 表の回数 + 1 = 56 + 1 = 57
- β = 裏の回数 + 1 = 44 + 1 = 45
このベータ分布
以下、コードです。
# ベータ分布
## ライブラリー読み込み
from scipy.stats import beta
import numpy as np
import matplotlib.pyplot as plt
## グラフの表示設定
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ
## 計算
a = 56+1
b = 44+1
x = np.linspace(0, 1, 100) #x軸
y = beta.pdf(x, a, b) #y軸
## 平均値、最頻値
print("mean = ",a/(a+b))
print("mode = ",(a-1)/(a+b-2))
## グラフ
plt.plot(x, y)
以下、実行結果です。
このベータ分布の横軸は「表の出る確率」で、縦軸が確率密度です。
この分布の中で最も確率密度が高くなる横軸の値を最頻値(mode)と呼びます。最も確率密度が高くなるとは、最も可能性が高い、ということです。
つまり、最も可能性が高い「表の出る確率」を知るには、最頻値(mode)を見ればいいとなります。
最頻値(mode)は、0.56です。
要するに、今得られたデータをもとに考えたとき、最も可能性が高い「表の出る確率」は、0.56ということです。
今回は、特定の値が1つ(「表の出る確率」が0.56)だけ得られたわけではなく、その分布が得られていることに注目してください。
ちなみに今回のコイン投げのように、2値のデータを扱うとき、要はどちらか一方の出現率(例:表の出る確率)を扱うとき、ベータ分布を仮定することが多いです。
ベイズ定理を知ろう!
先ず、ベイズの定理を紹介します。
高校生ぐらいで学んだかと思います。もしかしたら、高校ぐらいで学んだものとは、ちょっと表記と言うか名称が異なるかもしれません。気にしないでください。
以下が、ベイズの定理です。
- 推定対象:
- データ:
- 事前分布(prior):
- 尤度(likelhood):
- 規格化定数(normalization):
- 事後分布(posterior):
これは、得られたデータ(
更新前の推定対象(
更新後の推定対象(
最尤法
推定対象(
最尤法は、尤度(likelhood)が最大にする
コインを1回投げたときの尤度
コインを5回投げたときの尤度
例えば、表・裏・表・表・裏であった場合、以下のようになります。
コインを100回投げ、表が56回、裏が44回出た場合には、以下のようになります。
表の出る確率
細かい説明は省きますが、先程登場したベータ分布の最頻値(mode)の0.56になります。
ベイズアプローチ
先程示したベイズの定理の数式に、
事後分布
推定対象である
その事前分布に、先ほど登場したベータ分布を設定します。
事前分布(ベータ分布)のもとで、新たに取得したデータ(例:表 or 裏を記録した0-1データ)で更新し求めた事後分布
事前分布が
複雑そうに見えますが、要は事前分布
コイン投げのようなケースは非常に幸運で、数式に代入するだけで簡単に事後分布を導き出すことができます。
通常は、このように簡単にはいきません。
なぜならば、
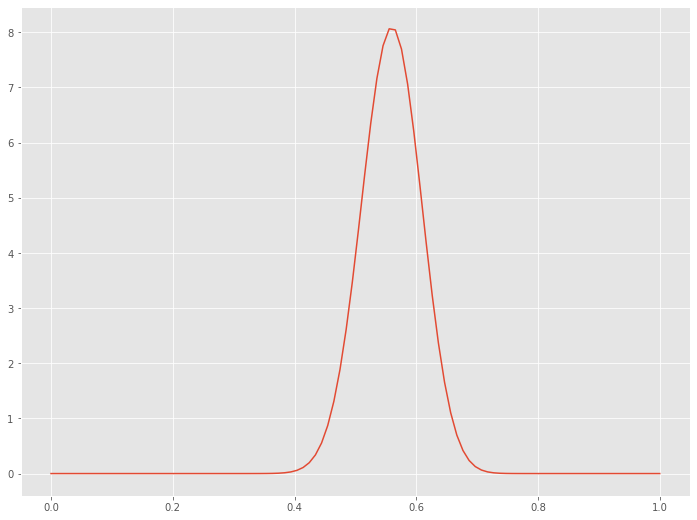
では、この幸運な状況を活用して、無情報事前分布に対し、コインを100回投げたら表が56回、裏が44回出たというデータを使い更新し求めた事後分布を見てみます。
先ずは、無情報事前分布を求めます。
今回のようにパラメータを設定することで、ベータ分布の無情報事前分布を作ることができます。
- α = 表の回数 + 1 = 0 + 1 = 1
- β = 裏の回数 + 1 = 0 + 1 = 1
どのような分布になるのでしょうか。Pythonで描いてみます。
以下、コードです。
## 計算
a = 1
b = 1
x = np.linspace(0, 1, 100) #x軸
y = beta.pdf(x, a, b) #y軸
## 平均値、最頻値
print("mean = ",a/(a+b))
## グラフ
plt.plot(x, y)
以下、実行結果です。
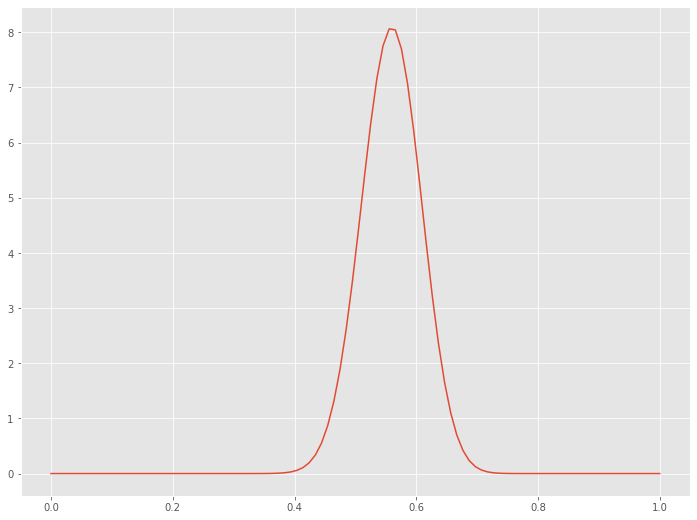
統計学で言うところの、一様分布になります。
次に、この無情報事前分布から事後分布を求めてみます。
以下、コードです。
## 計算
a = 57
b = 45
x = np.linspace(0, 1, 100) #x軸
y = beta.pdf(x, a, b) #y軸
## 平均値、最頻値
print("mean = ",a/(a+b))
print("mode = ",(a-1)/(a+b-2))
## グラフ
plt.plot(x, y)
以下、実行結果です。
これは、
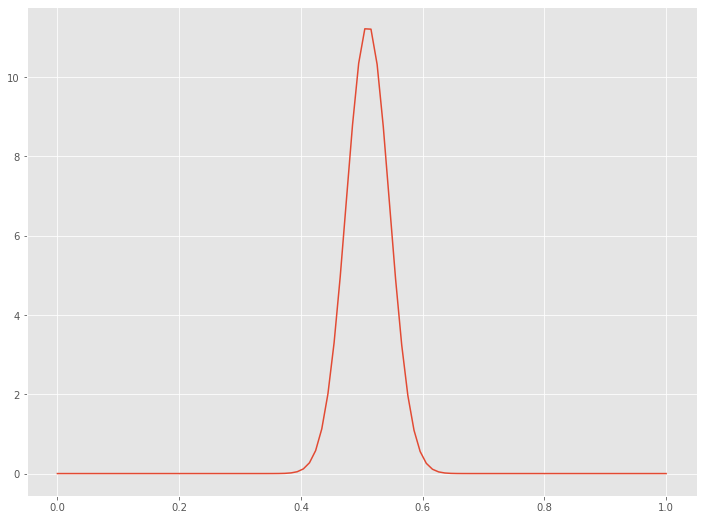
さらにコインを100回投げてみたら、表が46回、裏が54回でした。
この場合の事後分布を見てみます。
事前分布
以下、コードです。
## 計算
a = 46+57
b = 54+45
x = np.linspace(0, 1, 100) #x軸
y = beta.pdf(x, a, b) #y軸
## 平均値、最頻値
print("mean = ",a/(a+b))
print("mode = ",(a-1)/(a+b-2))
## グラフ
plt.plot(x, y)
以下、実行結果です。
まとめ
今回は、「コイン投げの例を使ってベイズ推定を何となく理解しよう」というお話しをしました。
今回は、PyMC3は登場しませんでした。コイン投げの場合、登場するまでもない、という感じでしたが、通常はそうは行きません。
次回は、「コイン投げの例を使ってPyMC3ベイズ推定を何となく理解しよう」というお話しをします。