最適化問題をPythonのPyomoライブラリーで解こう

その1：線形計画問題

14749
最適化問題をPythonのPyomoライブラリーで解こうその1：線形計画問題

最適化問題は、マーケティング予算配分の最適化、配送ルートの最適化、スケジュール最適化など、何かを最適化する問題を扱うものです。

最適化問題には、登場する数式や最適解の条件などによって、線形計画問題や非線形計画問題、混合整数計画問題などがあります。

基本となるのが、線形計画問題です。線形式しか登場しません。

線形式だけではなく非線形式を含めたのが非線形計画問題です。線形計画問題と比べ、解くのがだいぶ難しくなります。

混合整数計画問題は、解の一部が整数値をとる必要があるもので、場合によっては解くのが非常に難しく、組み合わせ最適化問題ともいわれます。

今回は、「最適化問題のとっても基礎的なお話しと線形計画問題」についてお話しします。

最適化の構成要素

最適化には3つの構成要素があります。

  • 目的関数
  • 変数
  • 制約条件

「ある制約条件のもと目的関数を最適化する変数を見つける」のが最適化問題です。

目的関数の最適化には2種類あります。

  • 目的関数を最大化
  • 目的関数の最小化

要は、最適化問題といっても、最大化問題と最小化問題の2種類あるということです。

最大化問題の場合、目的関数を最大化する変数が最適解であり、そのときの目的関数の値が最適値になります。最小化問題の場合、目的関数を最小化する変数が最適解であり、そのときの目的関数の値が最適値になります。

モデリングツールとソルバー

最適化問題を解くには、次の2つのツールが必要になります。

  • モデリングツール；最適化問題を記述するためのツール
  • ソルバー：記述された最適化問題を計算するためのツール

Pyomoは、モデリングツールです。

そのため、ソルバーを別途準備する必要があります。

ソルバーには、有料のものと無料のものがあり、Pypmoで利用できるソルバーは決まっていきます。

ソルバーは別途インストールする必要があります。

今回は、線形計画問題を解くための無料のソルバーである、GLPK（GNU Linear Programming Kit)を利用します。

Pyomoのインストール

PyomoとGLPKをcondaでインストールするときは、以下です。

conda install -c conda-forge pyomo
conda install -c conda-forge glpk

 

pipでもインストールできます。以下です。

pip install pyomo
pip install glpk

 

最適化問題のモデリングし解くまでの流れ

今回の最適化問題のモデリングし解くまでの流れを簡単に説明します。

以下です。

  1. モデリング
    1. モデルのインスタンスの生成
    2. 変数の定義
    3. 目的関数の定義
    4. 制約条件の定義
  2. 最適化
    1. ソルバーの設定
    2. 最適化の実施
  3. 結果確認

非常にシンプルです。

 

必要なモジュールの読み込み

先ずは、利用するモジュールを読み込みます。

以下、コードです。

# 必要なモジュールの読み込み
import pyomo.environ as pyo
from pyomo.opt import SolverFactory

 

今回、最適化する問題

今回、最適化する問題です。最小化問題です。

\displaystyle\begin{aligned}& \underset{x} \text{min} && f(x_1,x_2) = 75 x_1 + 125 x_2 \\& \text{subject to} && 6x_1 + 3x_2 \ge 38 \\&&& 5x_1 + 21x_2 \ge 29\\\end{aligned}

さらに、変数に幾つかの制約をつけた場合、どうなるのかを見ていきます。

今回は、変数への制約の付け方を、次の3パターンで設定し見ていきます。

  • 変数に非負制約あり
  • 変数に範囲制約あり
  • 変数に整数制約と範囲制約あり

 

最適解の計算

　変数に制約なし

先ず、モデリングです。

モデルのインスタンスを生成します。

以下、コードです。

model = pyo.ConcreteModel()

 

変数を定義します。x_1とx_2の2変数です。

以下、コードです。

model.x1 = pyo.Var()
model.x2 = pyo.Var()

 

次の目的関数を定義します。

\displaystyle \begin{aligned} && f(x_1,x_2) = 75 x_1 + 125 x_2 \end{aligned}

目的関数を数式として表現し関数として定義した後に、その関数を目的関数に設定します。

以下、コードです。

# 目的関数の数式の定義
def ObjRule(model):
    return 75*model.x1 + 125*model.x2

# 目的関数として設定
model.obj = pyo.Objective(rule = ObjRule,
                          sense = pyo.minimize)

 

次の2つの制約条件を定義します。

\displaystyle \begin{aligned} &&& 6x_1 + 3x_2 \ge 38 \\ &&& 5x_1 + 21x_2 \ge 29\\ \end{aligned}

制約条件を数式として表現し関数として定義した後に、その関数を制約条件に設定します。

以下、コードです。

## 制約条件の数式の定義

### 制約1
def Construle1(model):
    return 6*model.x1 + 3*model.x2 >= 38

### 制約2
def Construle2(model):
    return 5*model.x1 + 21*model.x2 >= 29

## 制約条件として設定
model.eq1 = pyo.Constraint(rule = Construle1)
model.eq2 = pyo.Constraint(rule = Construle2)

 

モデリングが終了したので、ソルバーを設定し最適化します。

以下、コードです。

# 最適化

## ソルバーの設定
opt = pyo.SolverFactory('glpk')

## 最適化の実施
res = opt.solve(model)

 

結果を確認します。

以下、コードです。

# 結果確認
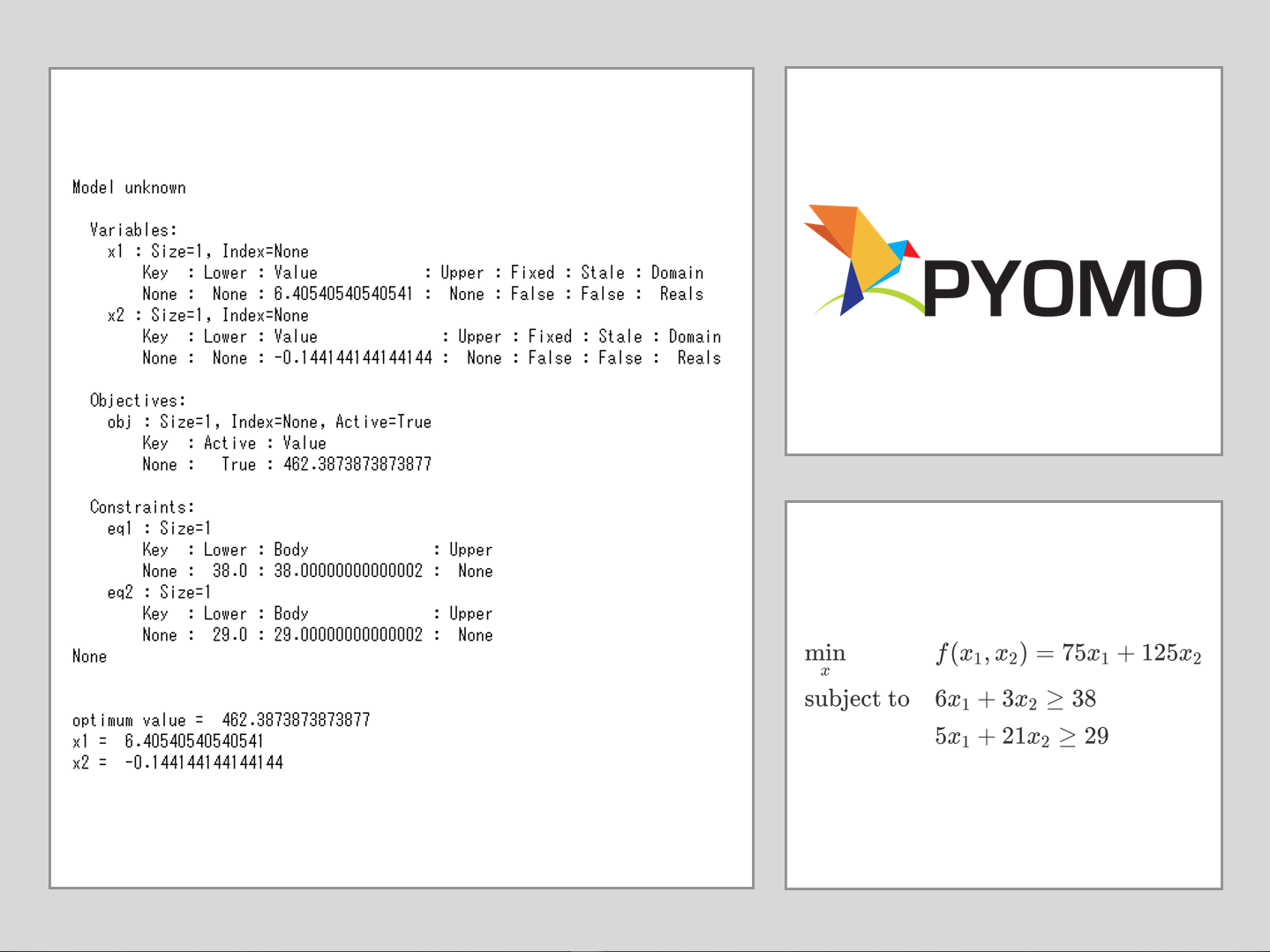
print(model.display())
print('\n')
print('optimum value = ', model.obj())
print("x1 = ", model.x1())
print("x2 = ", model.x2())

 

以下、実行結果です。

 

最適解は……

\displaystyle \begin{aligned} &&& x_1 = 6.40540540540541\\ &&& x_2 = -0.144144144144144\\ \end{aligned}

 

最適値（最小値）は……

\displaystyle \begin{aligned} && f(x_1,x_2) = 462.3873873873877 \end{aligned}

 

　変数に制約をつけるとき

変数の取る範囲に制約をつけることができます。

例えば……

  • 非負制約をつける
  • 範囲制約をつける
  • 整数制約をつける

……などなど。

先程のコードのVar()の中のカッコの中に設定します。

model.x1 = pyo.Var()
model.x2 = pyo.Var()

 

非負制約や整数制約などを付ける場合にはdomainに設定し、範囲制約を付ける場合にはboundsに設定します。

変数に非負制約をつけると、次のようになります。

model.x1 = pyo.Var(domain=pyo.NonNegativeReals)
model.x2 = pyo.Var(domain=pyo.NonNegativeReals)

 

変数に範囲制約をつけると、次のようになります。

model.x1 = pyo.Var(bounds=(-5, 5)) #-5から5の範囲
model.x2 = pyo.Var(bounds=(0, 10)) #0から10の範囲

 

変数に整数制約と範囲制約をつけると、次のようになります。

model.x1 = pyo.Var(domain=pyo.Integers, bounds=(-5, 5))
model.x2 = pyo.Var(domain=pyo.Integers, bounds=(0, 10))

 

それぞれの実行例を見てみます。先程と変えた行に色をつけています。

 

　変数に非負制約あり

変数に非負制約をつけた場合です。

以下、コードです。

#
# モデルのインスタンスの生成
#

model = pyo.ConcreteModel()

#
# 変数の定義
#

model.x1 = pyo.Var(domain=pyo.NonNegativeReals)
model.x2 = pyo.Var(domain=pyo.NonNegativeReals)

#
# 目的関数
#

## 目的関数の数式の定義
def ObjRule(model):
    return 75*model.x1 + 125*model.x2

## 目的関数として設定
model.obj = pyo.Objective(rule = ObjRule,
                          sense = pyo.minimize);

#
# 制約条件
#

## 制約条件の数式の定義

### 制約1
def Construle1(model):
    return 6*model.x1 + 3*model.x2 >= 38

## 制約2
def Construle2(model):
    return 5*model.x1 + 21*model.x2 >= 29

## 制約条件として設定
model.eq1 = pyo.Constraint(rule = Construle1)
model.eq2 = pyo.Constraint(rule = Construle2)

#
# 最適化
#

## ソルバーの設定
opt = pyo.SolverFactory('glpk')

## 最適化の実施
res = opt.solve(model)

#
# 結果確認
#

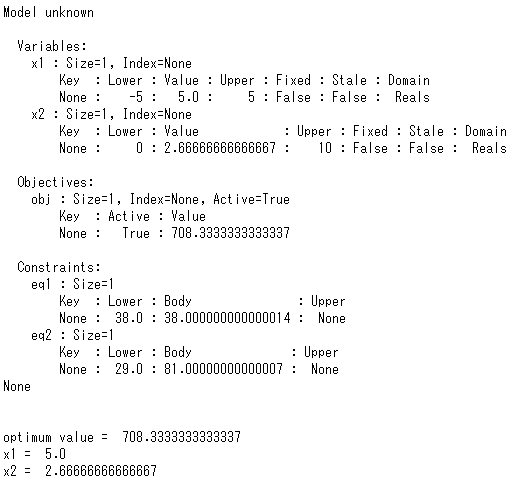
print(model.display())
print('\n')
print('optimum value = ', model.obj())
print("x1 = ", model.x1())
print("x2 = ", model.x2())

 

以下、実行結果です。

 

　変数に範囲制約あり

変数に範囲制約をつけた場合です。

以下、コードです。

#
# モデルのインスタンスの生成
#

model = pyo.ConcreteModel()

#
# 変数の定義
#

model.x1 = pyo.Var(bounds=(-5, 5))
model.x2 = pyo.Var(bounds=(0, 10))

#
# 目的関数
#

## 目的関数の数式の定義
def ObjRule(model):
    return 75*model.x1 + 125*model.x2

## 目的関数として設定
model.obj = pyo.Objective(rule = ObjRule,
                          sense = pyo.minimize);

#
# 制約条件
#

## 制約条件の数式の定義

### 制約1
def Construle1(model):
    return 6*model.x1 + 3*model.x2 >= 38

## 制約2
def Construle2(model):
    return 5*model.x1 + 21*model.x2 >= 29

## 制約条件として設定
model.eq1 = pyo.Constraint(rule = Construle1)
model.eq2 = pyo.Constraint(rule = Construle2)

#
# 最適化
#

## ソルバーの設定
opt = pyo.SolverFactory('glpk')

## 最適化の実施
res = opt.solve(model)

#
# 結果確認
#

print(model.display())
print('\n')
print('optimum value = ', model.obj())
print("x1 = ", model.x1())
print("x2 = ", model.x2())

 

以下、実行結果です。

 

　変数に整数制約と範囲制約あり

変数に整数制約と範囲制約をつけた場合です。

以下、コードです。

#
# モデルのインスタンスの生成
#

model = pyo.ConcreteModel()

#
# 変数の定義
#

model.x1 = pyo.Var(domain=pyo.Integers, bounds=(-5, 5))
model.x2 = pyo.Var(domain=pyo.Integers, bounds=(0, 10))

#
# 目的関数
#

## 目的関数の数式の定義
def ObjRule(model):
    return 75*model.x1 + 125*model.x2

## 目的関数として設定
model.obj = pyo.Objective(rule = ObjRule,
                          sense = pyo.minimize);

#
# 制約条件
#

## 制約条件の数式の定義

### 制約1
def Construle1(model):
    return 6*model.x1 + 3*model.x2 >= 38

## 制約2
def Construle2(model):
    return 5*model.x1 + 21*model.x2 >= 29

## 制約条件として設定
model.eq1 = pyo.Constraint(rule = Construle1)
model.eq2 = pyo.Constraint(rule = Construle2)

#
# 最適化
#

## ソルバーの設定
opt = pyo.SolverFactory('glpk')

## 最適化の実施
res = opt.solve(model)

#
# 結果確認
#

print(model.display())
print('\n')
print('optimum value = ', model.obj())
print("x1 = ", model.x1())
print("x2 = ", model.x2())

 

以下、実行結果です。

 

まとめ

今回は、「とっても最適化問題の基礎的なお話しと線形計画問題」についてお話ししました。

例で登場した最適化問題は小規模のものでしたが、現実は変数や数式の数は数百、数千、数万になります。

その場合、今回のように1つ1つ数式を定義していくことは現実的ではありません。

例えば、数式の係数や変数の上限や下限の制約を、外部からデータとして取得し、設定することが多いです。

次回は、「行列とベクトルを使った線形計画問題」というお話しをします。今回と同じ最適化問題を扱います。

最適化問題をPythonのPyomoライブラリーで解こうその2：線形計画問題（行列とベクトルを利用）