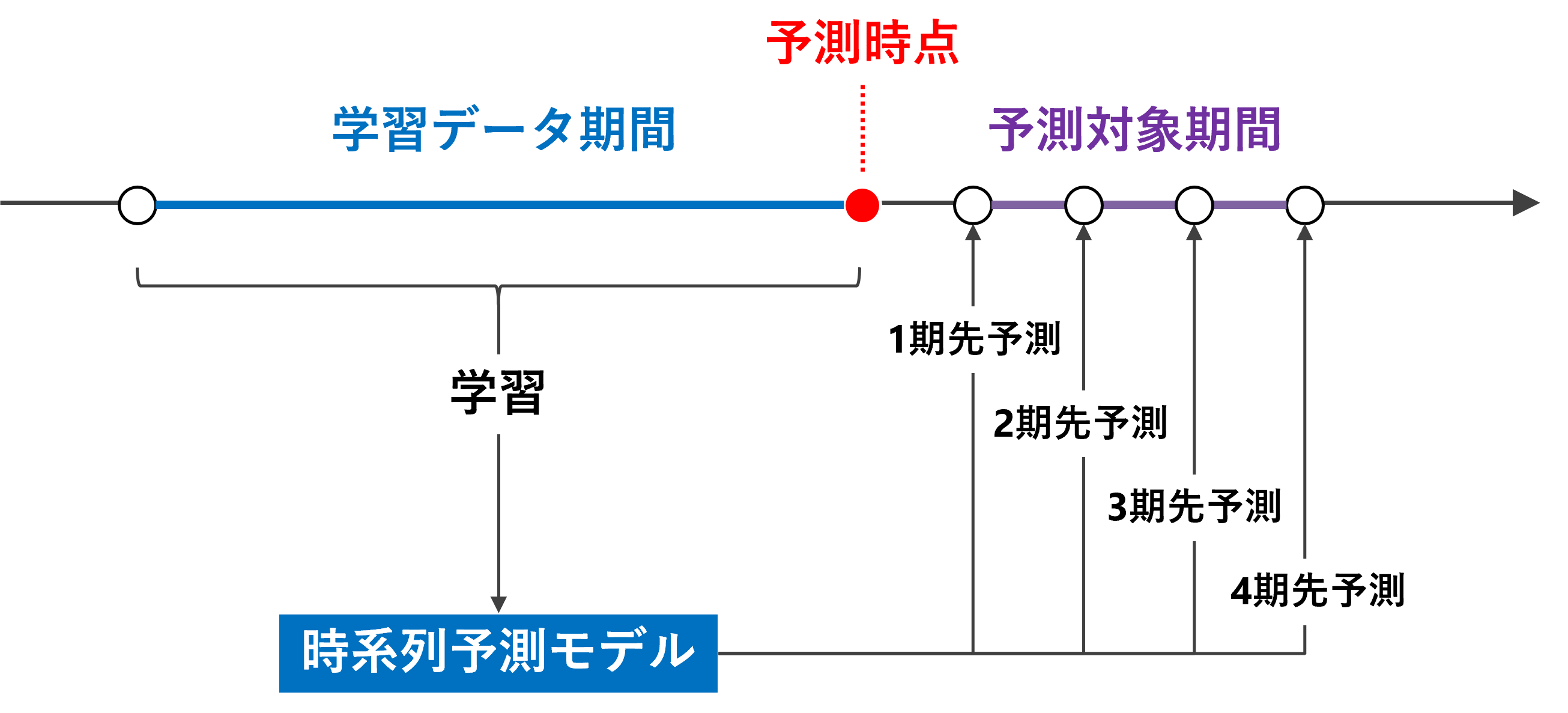
Pythonで時系列解析・超入門（その11）テーブルデータ系モデルで複数先予測（線形回帰）

時系列予測モデルの基本は1期先予測です。

例えば、時系列データが日単位である場合、1期先予測とは、学習データ期間の次の日を予測することです。

実務上は、1期先だけではなく、もっと先を予測することが多いです。

例えば、2期先予測（翌々日）、3期先予測（翌翌々日）、…などです。

複数先予測（Multi-Step ahead prediction）です。

ここで1つ問題が起こります。

予測モデルは、学習データ期間のデータを使いモデル構築します。

1期先予測であれば問題はないのですが、2期先を予測する場合そうはいきません。

1期先予測対象日の前日は学習データ期間であっても、2期先予測対象日の前日は学習データ期間ではありません。1期先予測対象日であり、学習データ期間外です。

どうすればいいでしょうか？

時系列系の数理モデル（ARIMAやProphetなど）の場合には、ツールで予測モデルを構築し予測をするとき、そのことを考慮し複数先予測（Multi-Step ahead prediction）
をしてくれます。

問題は、テーブルデータ系での数理モデル（線形回帰モデル、決定木、XGBoostなど）で、時系列の予測モデルを構築し、複数先予測（Multi-Step ahead prediction）
をするときです。

テーブルデータ系での数理モデル（線形回帰モデル、決定木、XGBoostなど）による時系列予測は、1期先予測しかしてくれません。

複数先予測（Multi-Step ahead prediction）をする方法がいくつかあります。よくある方法が以下の4つです。

n期先予測モデルを個々に作る方法（観測データのみ利用）
1期先予測モデルを1つ作り再帰的に利用する方法
n期先予測モデルを個々に作る方法（観測データ＋予測データ）
時系列の多変量予測モデルを1つ作る方法

それぞれについては、以下の記事で説明していますので、参考にして頂ければと思います。

第275話｜時系列予測モデルの複数先予測（Multi-Step ahead prediction）

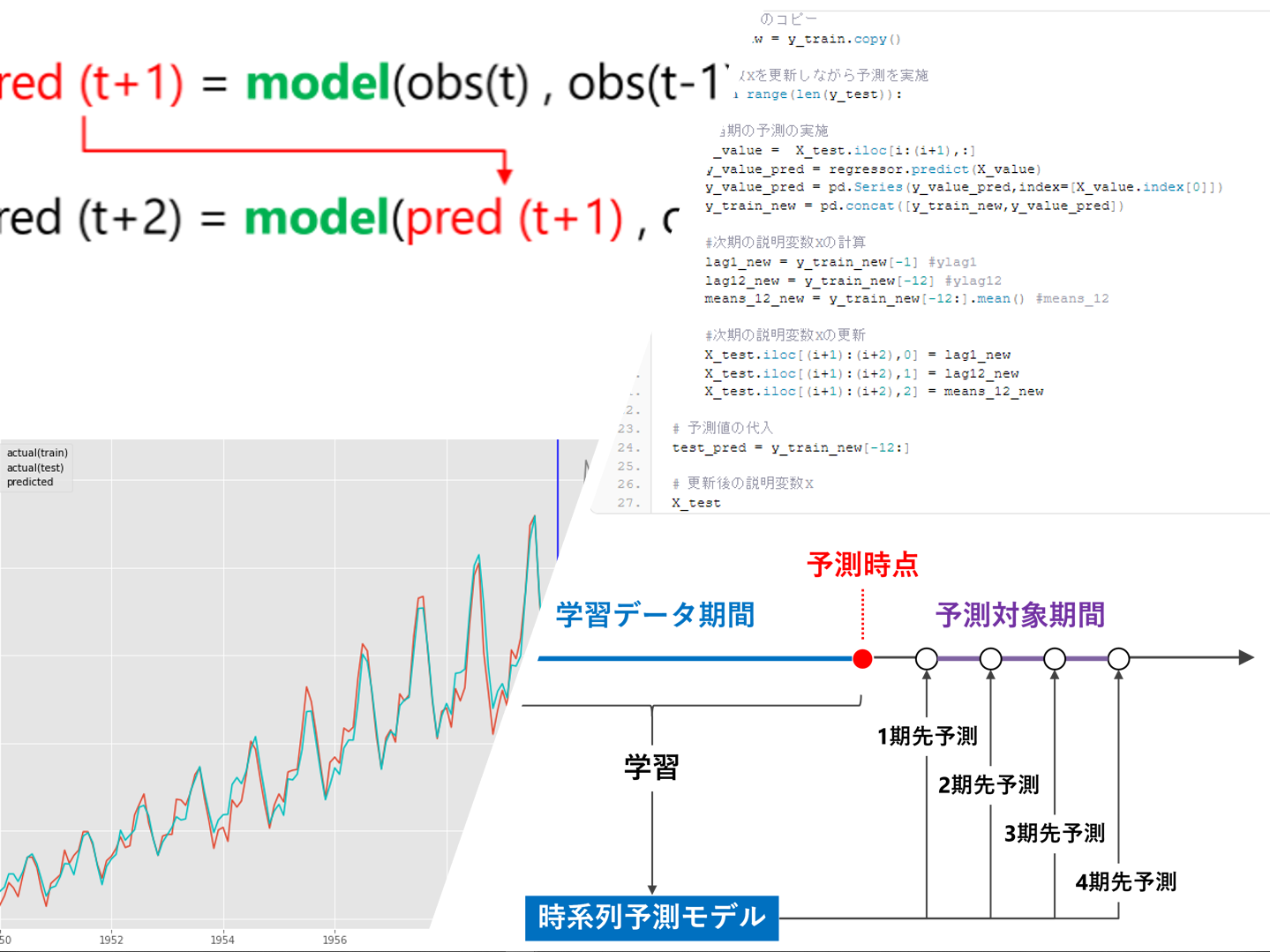
今回は、2番目の「1期先予測モデルを1つ作り再帰的に利用する方法」で「複数先予測」（Multi-Step ahead prediction）を実施していきます。予測モデルは、線形回帰モデルで構築します。

Contents

1期先予測モデルを1つ作り再帰的に利用する方法
必要なライブラリーの読み込み
利用するデータ
予測精度の評価指標
線形回帰モデルで予測モデル構築
　学習データで学習
　予測の実施（学習期間）
　予測の実施（テストデータ期間）
　予測モデルのテスト（テストデータ利用）
まとめ

1期先予測モデルを1つ作り再帰的に利用する方法

簡単に、「1期先予測モデルを1つ作り再帰的に利用する方法」について説明します。

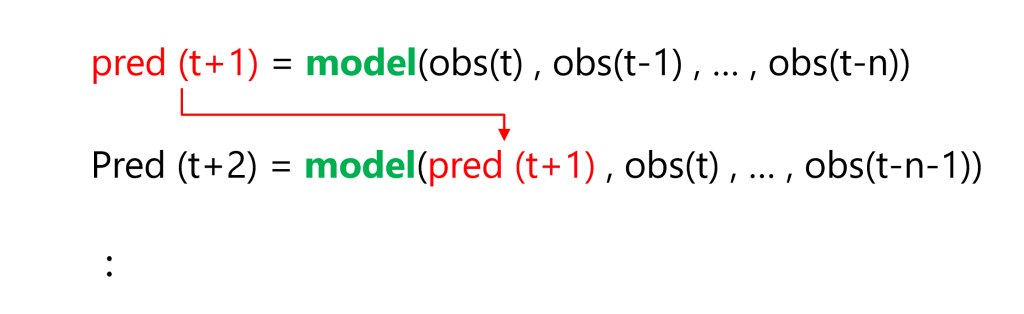
1期先予測モデルを使いまわして、複数先予測を実現しようという考え方です。

例えば、過去90日間のデータを使う予測モデルの場合、利用するデータ期間をスライドさせながら……

1期先予測：1期先予測対象日前の過去90日間のデータを使う
2期先予測：1期先予測対象日前の過去89日間のデータ＋前日の予測値のデータを使う
3期先予測：1期先予測対象日前の過去88日間のデータ＋前日と前々日の予測値のデータを使う

……といった感じで、予測データを使いながら予測を実施します。

予測モデルが1つで済むというのが利点です。ただ、2期先予測、3期先予測、……をするとき、その前までの予測値を過去の観測データの代わりに予測データを利用するという気持ち悪さは生まれます。

必要なライブラリーの読み込み

先ず、必要なライブラリーなどを読み込みます。

以下、コードです。

import numpy as np
import pandas as pd
import datetime

from sklearn.linear_model import LinearRegression

from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

利用するデータ

今回利用するデータは、前回準備した時系列特徴量付きデータセットです。

以下からダウンロードできます。

dataset.csv
https://www.salesanalytics.co.jp/6ro8

このURLから直接データセットを読み込めます。

以下、コードです。

url='https://www.salesanalytics.co.jp/6ro8'
df=pd.read_csv(url,                         #読み込むデータのURL
               index_col='Month',           #変数「Month」をインデックスに設定
               parse_dates=True)            #インデックスを日付型に設定
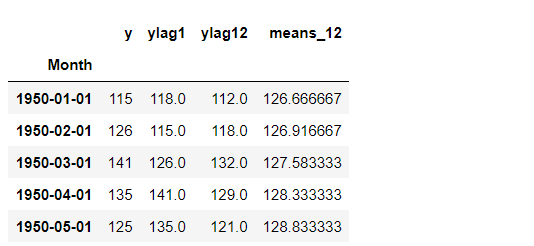
df.head() #確認

以下、実行結果です。

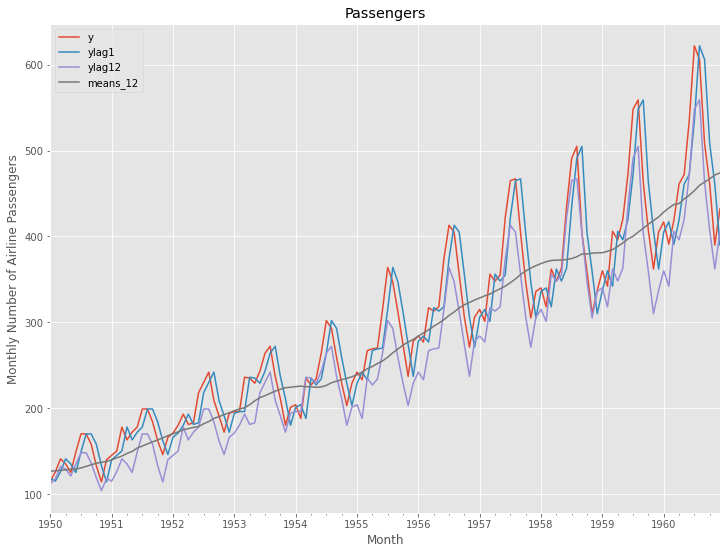
グラフ化し確認します。

以下、コードです。

# プロット
df.plot()
plt.title('Passengers')                            #グラフタイトル
plt.ylabel('Monthly Number of Airline Passengers') #タテ軸のラベル
plt.xlabel('Month')                                #ヨコ軸のラベル
plt.show()

以下、実行結果です。

次に、読み込んだデータセットを、学習データとテストデータに分割します。

以下、コードです。

# 学習データ
train = df.iloc[:-12]
y_train = train['y']              #目的変数y
X_train = train.drop('y', axis=1) #説明変数X

# テストデータ
test = df.iloc[-12:]  #テストデータ
y_test = test['y']              #目的変数y
X_test = test.drop('y', axis=1) #説明変数X

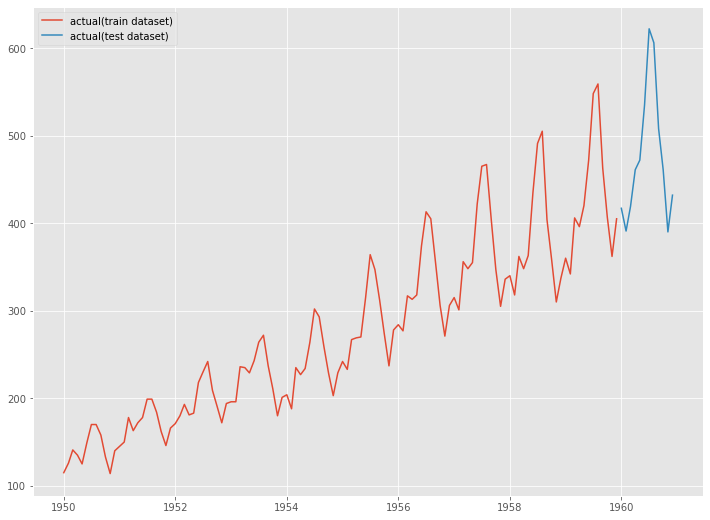
グラフ化します。

以下、コードです。

# グラフ化
fig, ax = plt.subplots()
ax.plot(y_train.index, y_train.values, label="actual(train dataset)")
ax.plot(y_test.index, y_test.values, label="actual(test dataset)")
plt.legend()

以下、実行結果です。

学習データで線形回帰モデルを構築し、構築したモデルをテストデータで精度検証します。

ただ、このテストデータの説明変数Xをそのまま使うわけではありません。

テストデータの説明変数Xを見てみます。

以下、コードです。

# テストデータ
X_test

以下、実行結果です。

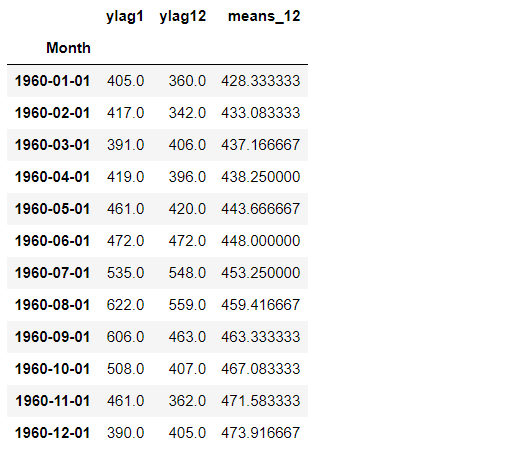
例えば、「1960-12-01」の「ylag1」（yのラグ1）のデータは「390.0」となっていますが、そのデータを使い「1960-12-01」の「y」の値を予測するわけではありません。

「ylag1」（yのラグ1）のデータは「390.0」は、「1960-11-01」の「y」の実測値です。予測時に、予測対象の1つである「1960-11-01」の「y」の実測値は分かりません。分かるのは、「1960-11-01」の「y」の予測値です。

そのため、「1960-12-01」の「y」の値を予測するときに利用するのは、「1960-11-01」の「y」の実測値ではなく予測値です。

要は、テストデータの説明変数Xは、順次予測をしながら再計算し求め直します。

予測精度の評価指標

今回の予測精度の評価指標は、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使います。

以下の記号を使い精度指標の説明をします。

$y_i^{actual}$ ・・・ $i$ 番目の実測値
$y_i^{pred}$ ・・・ $i$ 番目の予測値
$n$ ・・・実測値・予測値の数

■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）

\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}

■ 平均絶対誤差（MAE、Mean Absolute Error）

\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|

■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）

\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|

線形回帰モデルで予測モデル構築

　学習データで学習

学習データを使って、線形回帰モデルを学習します。

以下、コードです。

regressor = LinearRegression()
regressor.fit(X_train, y_train)

これは、1期先予測モデルです。

　予測の実施（学習期間）

学習データ期間の目的変数yの値を予測します。学習データ期間の説明変数Xのデータは既知なので、学習し求めた予測モデルをそのまま利用します。

以下、コードです。

train_pred = regressor.predict(X_train)

　予測の実施（テストデータ期間）

テストデータ期間の目的変数yの値を予測します。テストデータ期間の説明変数Xのデータは未知のものが混在しているので、工夫が必要です。

要は、「1期先予測モデルを1つ作り再帰的に利用する方法」で「複数先予測」（Multi-Step ahead prediction）を実施していきます。

以下、コードです。

# 学習データのコピー
y_train_new = y_train.copy()

# 説明変数Xを更新しながら予測を実施
for i in range(len(y_test)):
    
    #当期の予測の実施
    X_value =  X_test.iloc[i:(i+1),:]
    y_value_pred = regressor.predict(X_value)
    y_value_pred = pd.Series(y_value_pred,index=[X_value.index[0]])
    y_train_new = pd.concat([y_train_new,y_value_pred])
    
    #次期の説明変数Xの計算
    lag1_new = y_train_new[-1] #ylag1
    lag12_new = y_train_new[-12] #ylag12
    means_12_new = y_train_new[-12:].mean() #means_12
    
    #次期の説明変数Xの更新
    X_test.iloc[(i+1):(i+2),0] = lag1_new
    X_test.iloc[(i+1):(i+2),1] = lag12_new
    X_test.iloc[(i+1):(i+2),2] = means_12_new
    
# 予測値の代入
test_pred = y_train_new[-12:]
    
# 更新後の説明変数X
X_test

以下、実行結果です。予測しながら更新したテストデータの説明変数Xです。

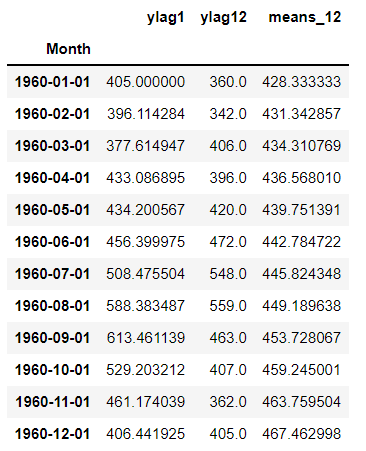
先程見た、テストデータの説明変数Xと、ところどころ値が異なっているのが分かるかと思います。

　予測モデルのテスト（テストデータ利用）

テストデータで精度検証します。

以下、コードです。

print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred)) 
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))

以下、実行結果です。

グラフ化します。

以下、コードです。

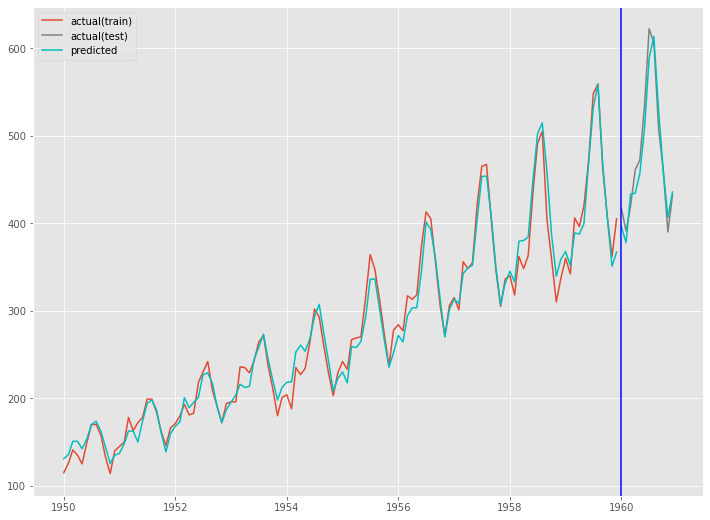
fig, ax = plt.subplots()

ax.plot(train.index, y_train, label='actual(train)')
ax.plot(test.index, y_test, label='actual(test)', color='gray')
ax.plot(train.index, train_pred, color='c')
ax.plot(test.index, test_pred, label="predicted", color="c") 
ax.axvline(datetime.datetime(1960,1,1),color='blue')
ax.legend()

plt.show()

以下、実行結果です。