時系列データには複数の季節性を持つ場合があります。
例えば、日単位の時系列データであれば週周期と年周期、時単位の時系列データであれば日周期と週周期などです。
時系列データでよく利用されるモデルは、ARIMA系のモデルです。季節性を考慮したARIMA系のモデルをSARIMAモデルといいます。
SARIMAモデルは、季節成分が1つの場合に対応し、複数には対応していません。
では、どうすればいいのか。
複数の季節性をもつ時系列モデルがあります。その1つがTBATSモデルです。以前お話ししました。
もっと身近なテーブルデータ系の数理モデル（線形回帰モデルや決定木モデル、XGBoostなど）でモデル化できなだろうかということで、線形回帰モデル（単回帰・重回帰）です。
テーブルデータ系の数理モデル（線形回帰モデルや決定木モデル、XGBoostなど）で、時系列の予測モデルなどを構築する場合、時系列特徴量というものを生成し、それをもとにテーブルデータを作る必要があります。
さらに、季節性を柔軟に表現する特徴量が必要なため、フーリエ級数に基づく三角関数による季節性表現を利用します。
今回は、「複数季節性を持つ時系列データを線形回帰でモデル化する方法」というお話しをします。
Contents
フーリエ級数に基づく三角関数による季節性表現
季節性の表現方法には幾つか種類があります。今回は、フーリエ級数に基づく、sinやcosなどの三角関数を利用した季節性表現を採用します。
簡単に説明します。
例えば、時系列データy_tに対し、考慮したい季節性がM個、各季節性の周期がp_i、各季節性のフーリエ項がK_i個（i=1,2,\cdots,M）、N_tが季節性以外の時系列成分とします。このとき、次のように表現できます。
\displaystyle y_t = a + \sum_{i=1}^M \sum_{k=1}^{K_i} [ \alpha_{i_k} \sin (\frac{2 \pi k t}{p_i}) + \beta_{i_k} \cos (\frac{2 \pi k t}{p_i}) ] + N_t M=1かつK_1=1の場合、その季節性はsinとcosの2変数で表現されます。pは周期です。 \displaystyle y_t = a + \alpha \sin (\frac{2 \pi t}{p}) + \beta \cos (\frac{2 \pi t}{p}) + N_t M=1かつK_1=2の場合、sinとcosのセットが2つ（4変数）で表現されます。pは周期です。 \displaystyle y_t = a + \alpha_1 \sin (\frac{2 \pi t}{p}) + \beta_1 \cos (\frac{2 \pi t}{p}) + \alpha_2 \sin (\frac{2 \pi 2t}{p}) + \beta_2 \cos (\frac{2 \pi 2t}{p}) + N_tsinとcosのセットが少ないと、季節性の表現が荒くなります。そう考えると、sinとcosのセットを増やせばいいのではとなりますが、変数が多くなります。
そこで、「sinとcosを何セット必要なのか」という問題がありますが、あまり多くないようにしましょう。
必要なモジュールを読み込む
必要なモジュール一式を読み込みます。
以下、コードです。
import numpy as np
import pandas as pd
import statsmodels.api as sm
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error
from pmdarima import model_selection
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定
必要なデータを読み込む
Rで提供されているサンプルデータtaylor（30分ごとの電力需要の時系列データ）を利用します。
taylor は、2000年6月5日（月）から8月27日（日）までのイングランドとウェールズにおける30分ごとの電力需要（メガワット）の時系列データです。
Rで提供されている1,500以上のサンプルデータをPythonから利用できます。利用してみたい方は、以下の記事を参考にしていただければと思います。
では、このデータを読み込みます。
以下、コードです。
dataset = sm.datasets.get_rdataset("taylor", "forecast")
y = dataset.data['x']
y #確認
以下、実行結果です。
グラフ化し見てみます。
以下、コードです。
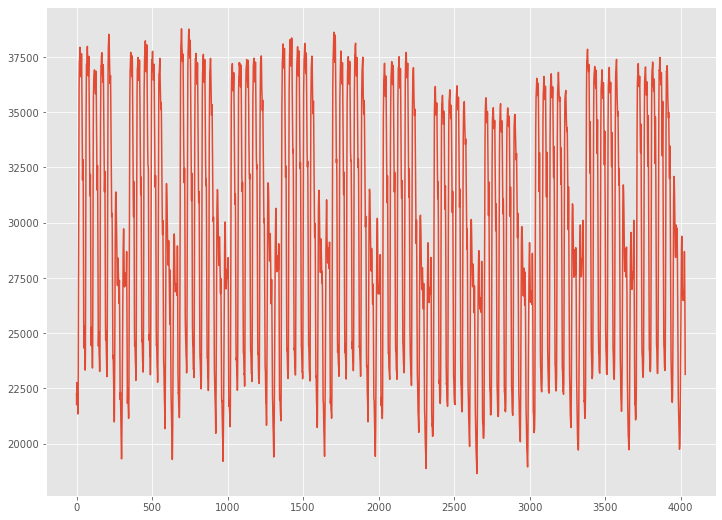
y.plot() plt.show()
以下、実行結果です。
時系列特徴量を生成しテーブルデータを構築
テーブルデータ系の数理モデルである線形回帰モデルでモデルを構築するため、テーブルデータを作る必要があります。
そのために、テーブルデータを生成するには、時系列特徴量を生成する必要があります。
今回は、以下の5つの時系列特徴量を生成します。
- ラグ1のラグ特徴量：lag1
- 前期（30分前）までの1日の平均であるローリング特徴量：window48
- 前期（30分前）までの全平均であるエクスパディング特徴量：expanding
- 三角関数により1日周期を表現する三角関数特徴量：sin48, cos48 × 10個
- 三角関数により7日周期（336周期）を表現する三角関数特徴量：sin336, cos336 × 10個
三角関数特徴量に関しては、それぞれ20個の特徴量を生成します。
先ず、ラグ特徴量およびローリング特徴量、エクスパディング特徴量を作成します。
以下、コードです。
# # ラグ特徴量・ローリング特徴量・エクスパディング特徴量 # # ラグ特徴量（ラグ1）の生成 lag1 = y.shift(1) # ローリング特徴量（1期前までの1日の平均） window48 = lag1.rolling(window=48).mean() # エクスパンディング特徴量（1期前までの平均） expanding = lag1.expanding().mean()
作成した時系列特徴量を結合しテーブルデータを生成します。
以下、コードです。
#
# 作成した時系列特徴量を結合しテーブルデータを生成
#
## データを結合
df_tbl = pd.concat([y,
lag1,
window48,
expanding
],
axis=1)
## 変数名を設定
df_tbl.columns = ['y',
'lag1',
'window48',
'expanding'
]
df_tbl #確認
以下、実行結果です。
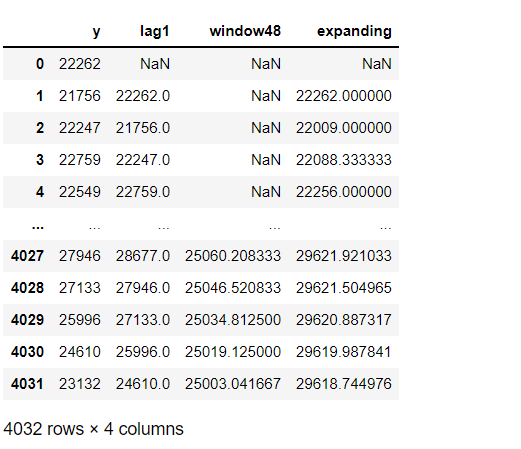
次に、三角関数特徴量を作成します。
以下、コードです。
#
# 三角関数特徴量
#
# 空のデータフレーム生成
exog = pd.DataFrame()
exog.index = y.index
# 三角関数特徴量（Fourier terms）の生成関数
def fourier_terms_gen(seasonal,terms_num):
#seasonal:周期
#terms_num:Fourier termの数（sinとcosのセット数）
for num in range(terms_num):
num = num + 1
sin_colname = 'sin'+str(seasonal)+'_'+ str(num)
cos_colname = 'cos'+str(seasonal)+'_'+ str(num)
exog[sin_colname] = np.sin(num * 2 * np.pi * exog.index / seasonal)
exog[cos_colname] = np.cos(num * 2 * np.pi * exog.index / seasonal)
# 三角関数により7日周期（336周期）を表現する三角関数特徴量
fourier_terms_gen(seasonal=336,
terms_num=10)
# 三角関数により1日周期（48周期）を表現する三角関数特徴量
fourier_terms_gen(seasonal=48,
terms_num=10)
exog #確認
以下、実行結果です。
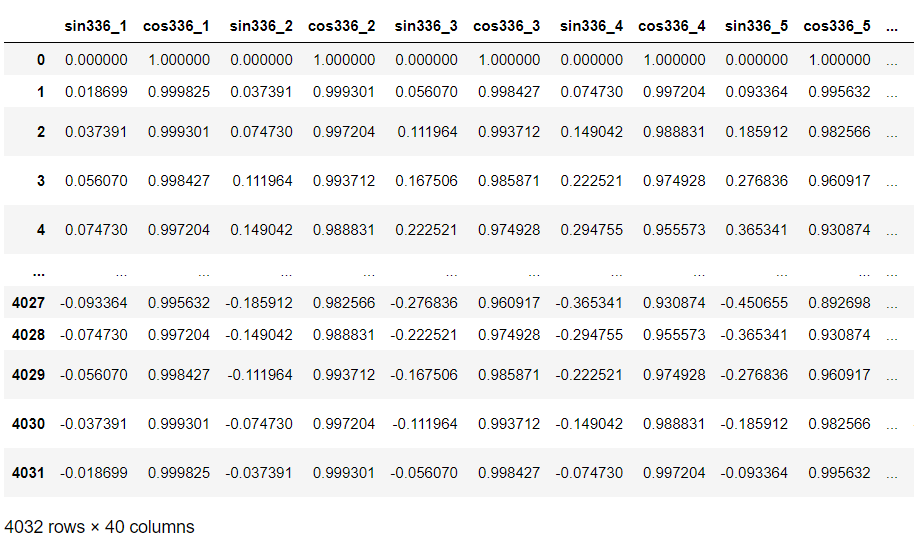
最後に、2つのテーブルデータを結合します。そして、欠測値が含まれているレコードがあるので削除します。
以下、コードです。
#
# 2つのテーブルデータの結合と欠測値削除
#
# データを結合
df_tbl = pd.concat([df_tbl,
exog,
],
axis=1)
# 欠測値削除
df_tbl = df_tbl.dropna()
df_tbl #確認
以下、実行結果です。
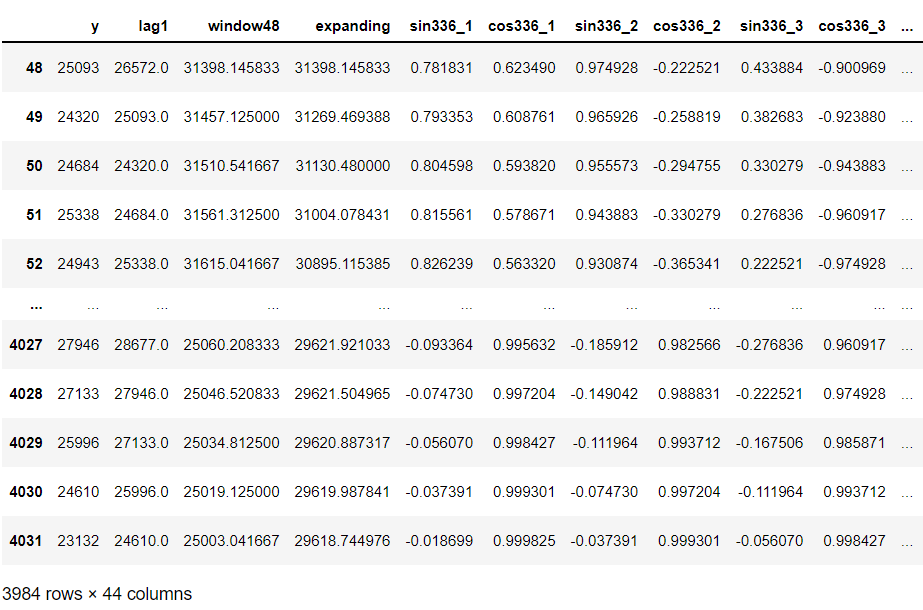
今回は、予測モデルを学習データで構築し、構築した予測モデルをテストデータ（後ろから7日間）で検証します。
学習データとテストデータを分解します。
以下、コードです。
#
# データセットを学習データとテストデータ（後ろから7日間）に分割
#
# データ分割
train, test = model_selection.train_test_split(df_tbl, test_size=336)
# 学習データ
y_train = train['y'] #目的変数y
X_train = train.drop('y', axis=1) #説明変数X
# テストデータ
y_test = test['y'] #目的変数y
X_test = test.drop('y', axis=1) #説明変数X
グラフ化し見てみます。
以下、コードです。
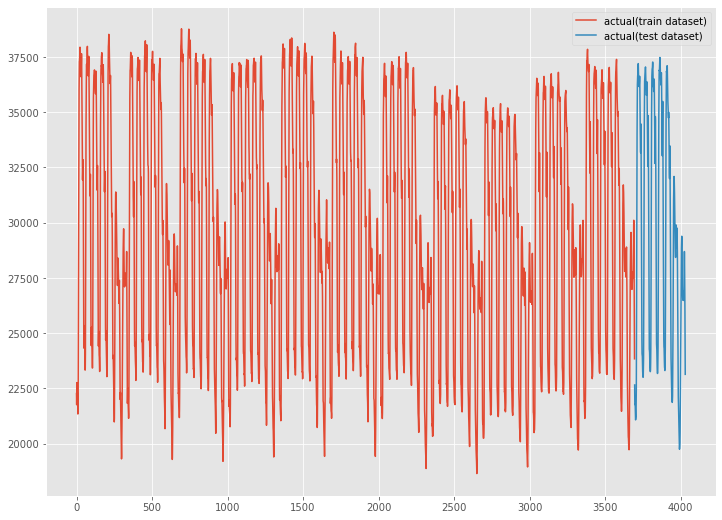
fig, ax = plt.subplots() ax.plot(y_train.index, y_train.values, label="actual(train dataset)") ax.plot(y_test.index, y_test.values, label="actual(test dataset)") ax.legend()
以下、実行結果です。
予測モデル（線形回帰）の学習
学習データで、予測モデル（線形回帰）を学習します。
以下、コードです。
# # モデル構築 # # インスタンス生成 regressor = LinearRegression() # 学習 regressor.fit(X_train, y_train)
予測の実施
学習データ期間を予測
先ずは、学習データ期間を予測します。
以下、コードです。
# # 予測の実施（学習期間） # train_pred = regressor.predict(X_train)
テストデータ期間を予測
次に、テストデータ期間を予測します。
テーブルデータ系の数理モデル（線形回帰モデルや決定木モデル、XGBoostなど）で時系列の予測モデルを学習し、学習で使ったデータ期間よりも未来を予測する場合に問題が起こります。
時系列系の数理モデル（ARIMA、Prophet、TBATSなど）は、複数先予測（Multi-Step ahead prediction）を実施することを前提にツール上で実装されているケースが多いですが、テーブルデータ系の数理モデル（線形回帰モデルや決定木モデル、XGBoostなど）の場合にはそうはいきません。
先程学習し求めた線形回帰の予測モデルは、1期先予測モデルです。2期先や3期先などの予測には使えません。ただ、この1期先予測モデルを使いまわして、複数先予測を実現しようという考え方があります。
予測結果を再帰的に利用し、複数先予測を実現するというものです。
今回は、この方法を使い複数先予測を実施します。
以下、コードです。
#
# 予測の実施（テストデータ期間）
#
# 学習データのコピー
y_train_new = y_train.copy()
# 説明変数Xを更新しながら予測を実施
for i in range(len(y_test)):
#当期の予測の実施
X_value = X_test.iloc[i:(i+1),:]
y_value_pred = regressor.predict(X_value)
y_value_pred = pd.Series(y_value_pred,index=[X_value.index[0]])
y_train_new = pd.concat([y_train_new,y_value_pred])
#次期の説明変数Xの計算
lag1_new = y_train_new.iloc[-1] #lag1
window48_new = y_train_new.iloc[-48:].mean() #window48
expanding_new = y_train_new.mean() #expanding
#次期の説明変数Xの更新
X_test.iloc[(i+1):(i+2),0] = lag1_new
X_test.iloc[(i+1):(i+2),1] = window48_new
X_test.iloc[(i+1):(i+2),2] = expanding_new
# 予測値の代入
test_pred = y_train_new[-336:]
予測モデル（線形回帰）の評価
評価指標の簡単な説明
構築した予測モデルは、RMSE（二乗平均平方根誤差、Root Mean Squared Error）とMAE（平均絶対誤差、Mean Absolute Error）、MAPE（平均絶対パーセント誤差、Mean absolute percentage error）を使い、予測精度の評価をしていきます。いずれの精度指標も値が小さいほど良いです。
以下の記号を使い精度指標の説明をします。
- y_i^{actual} ・・・i番目の実測値
- y_i^{pred} ・・・i番目の予測値
- n ・・・実測値・予測値の数
■ 二乗平均平方根誤差（RMSE、Root Mean Squared Error）
\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i^{actual}-{y_i^{pred}})^2}■ 平均絶対誤差（MAE、Mean Absolute Error）
\frac{1}{n}\sum_{i=1}^n|y_i^{actual}-{y_i^{pred}}|■ 平均絶対パーセント誤差（MAPE、Mean absolute percentage error）
\frac{1}{n}\sum_{i=1}^n|\frac{y_i^{actual}-{y_i^{pred}}}{y_i^{actual}}|
評価の実施
テストデータで、構築した予測モデルを評価します。
以下、コードです。
# 精度指標（テストデータ）
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, test_pred))
以下、実行結果です。
グラフ化し確認します。
以下、コードです。
# グラフ化（テストデータの期間）
fig, ax = plt.subplots()
ax.plot(y_test.index,
y_test.values,
label="actual(test dataset)")
ax.plot(y_test.index,
test_pred,
label="LinearRegression",
linestyle="dotted",
lw=2,
color="m")
ax.legend()
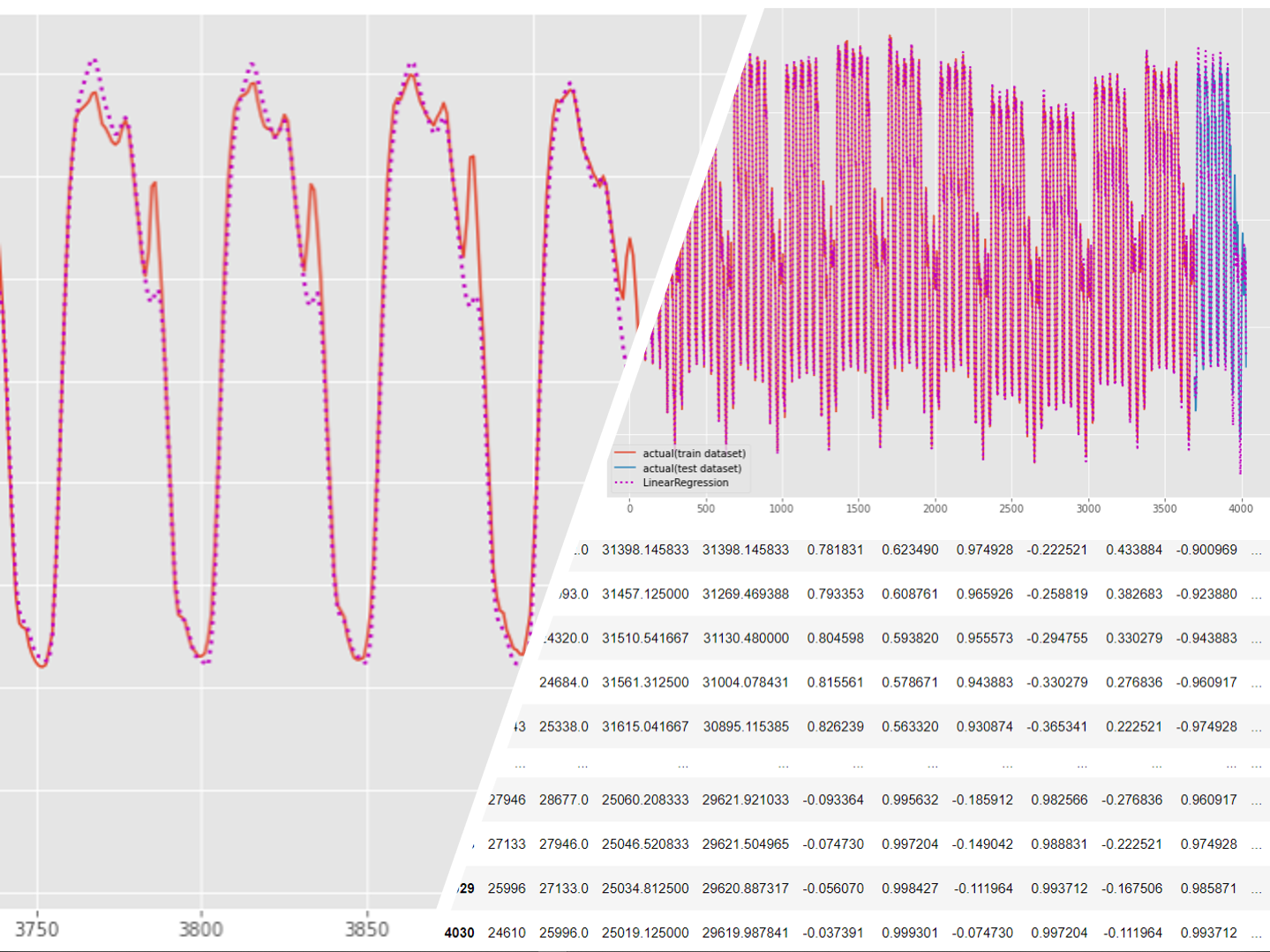
以下、実行結果です。
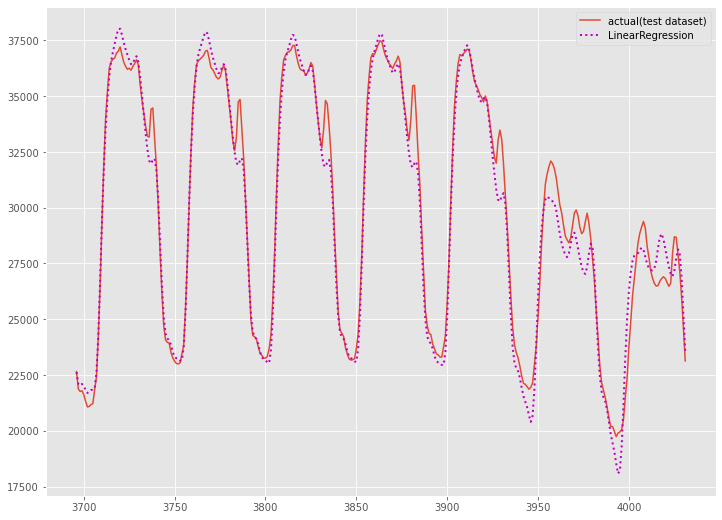
学習データを含めた全期間（学習データの期間＋テストデータの期間）をグラフ化し見てみます。
以下、コードです。
# グラフ化（全期間）
fig, ax = plt.subplots()
ax.plot(y_train.index,
y_train.values,
label="actual(train dataset)")
ax.plot(y_test.index,
y_test.values,
label="actual(test dataset)")
ax.plot(y_train.index,
train_pred,
linestyle="dotted",
lw=2,
color="m")
ax.plot(y_test.index,
test_pred,
label="TBATS",
linestyle="dotted",
lw=2,
color="m")
以下、実行結果です。
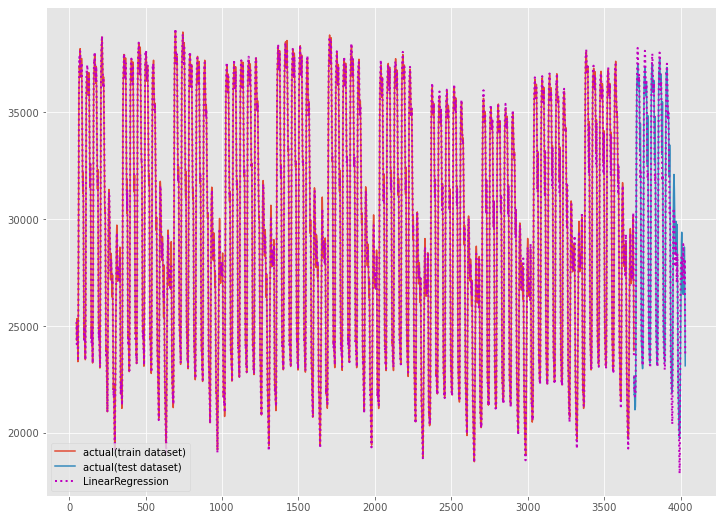
気になる予測精度ですが、それほど悪くはありません。もしかしたら、時系列系の数理モデル（ARIMA、Prophet、TBATSなど）よりもいいぐらいです。
実は、時系列特徴量をどう作成するのかが、大きく予測精度に影響します。特徴量生成に長けた方であれば、もっと高精度なモデルを構築できるかもしれません。
まとめ
今回は、「複数季節性を持つ時系列データを線形回帰でモデル化する方法」というお話しをしました。
三角関数特徴量を使うことで、身近なテーブルデータ系の数理モデル（線形回帰モデルや決定木モデル、XGBoostなど）でモデル化を実現できます。
興味のある方は、チャレンジしてみてください。
