相互相関で描く時系列グラフィカルモデリング（Python版）

グラフィカルモデリングとは、多変量データ（変数が複数あるデータセット）の変数間の構造を表す統計モデルをグラフによって表現したもので、小難しくいうと、確率変数間の依存関係をグラフ表現したものです。

変数間の関係を無向グラフや有向グラフなどで表現することで、視覚的に変数間の関係を把握することができます。

多変量時系列データに対するグラフィカルモデリングの1手法として、グレンジャー因果性に基づく方法があります。

グレンジャー因果性とは、ある時系列データAの過去の値が別の時系列データBの将来の値を予測する能力を有するというもので、予測的因果関係とも言われています。

先行指標の概念を持ち出せば、「Aの値の変化の後にBの値が変化している」というもので「Aは、Bの先行指標（先行系列）である」という感じです。

要は、「因果」という名称がついていますが、「因果」ではありません。そもそも、データから因果かどうかを特定することは、どのような手法を用いても、現代の技術で知ることは到底不可能かと思います。

グラフィカルモデリングの大きな問題として、どの変数間に線を引くのか、というい問題があります。

一番簡単なのは、相関の高い変数同士に線を引く、というものがあります。

今回扱うデータは時系列データですので、相互相関をもとに線を引くのが簡単かと思います。

ということで今回は、「相互相関と時系列グラフィカルモデリング」というお話しをします。

Contents

相互相関
必要なモジュールとデータの読み込み
相互相関をもとに有向グラフを描写
　データの標準化
　相互相関のコレログラム
　有向グラフ
まとめ

相互相関

相互相関は、通常の数理統計学で登場する相関係数を、単に時系列データに応用したもので、2つの時系列データの類似性を表現する指標です。

通常の相関係数との大きな違いは、時間をずらして相関係数を求めるところにあります。

1期ずれ、2期ずれ、3期ずれ、……のように一方の時系列データをずらして相関係数を求めます。

このずれをラグという表現で表したりします。例えば、1期ずれのことをラグ1、2期ずれのことをラグ2、3期ずれのことをラグ3、……などなど。

このような相関係数を求めることで、時系列データの季節性や因果関係などを検討する材料にします。

必要なモジュールとデータの読み込み

では、必要なモジュールを読み込みます。

以下、コードです。

import pandas as pd
import numpy as np
from scipy import stats

from graphviz import Digraph

from matplotlib import mlab
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

グラフは、graphvizライブラリーのモジュールで描きますので、インストールされていない方は、pip install graphvizなどのコードでインストールして頂ければとも思います。

次に、今回利用するデータを読み込みます。

以下、コードです。

# データセット読み込み
url = 'https://www.salesanalytics.co.jp/0olr'
df = pd.read_csv(url,
                 parse_dates=True,
                 index_col='day'
                )
df #確認

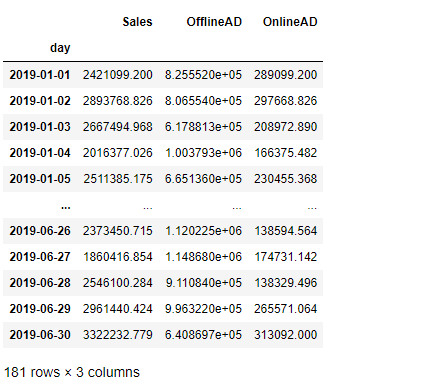
以下、実行結果です。

日単位の3変量の時系列データです。

Sales：売上
OfflineAD：TVCMなどのオフライン広告のコスト
OnlineAD：Webなどのオンライン広告のコスト

目的変数が「Sales」で、残りの2つが説明変数です。

どのような時系列データなのかを、折れ線グラフを描き確認します。

以下、コードです。

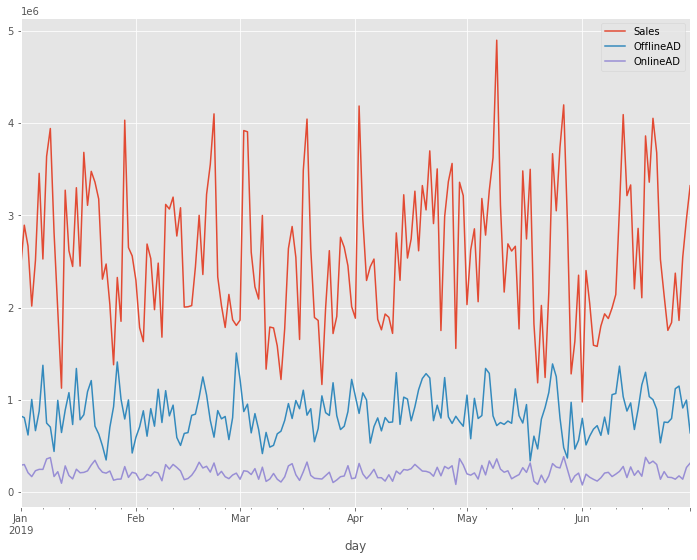
# グラフ化
df.plot()

以下、実行結果です。

相互相関をもとに有向グラフを描写

　データの標準化

相互相関を求める関数を使い、サクッと相互相関のコレログラムを作ってみます。

時系列データを標準化（平均0、分散1）します。

以下、コードです。

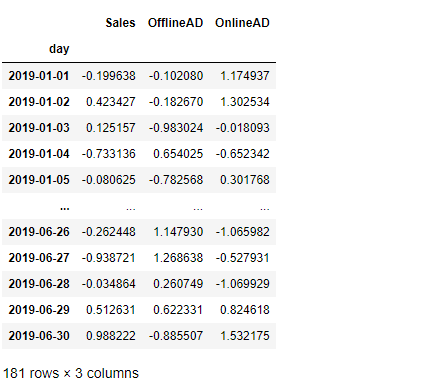
# 標準化（平均0、分散1）
df_std = stats.zscore(df)

df_std #確認

以下、実行結果です。

　相互相関のコレログラム

相互相関のコレログラムを作成します。

以下、コードです。

#
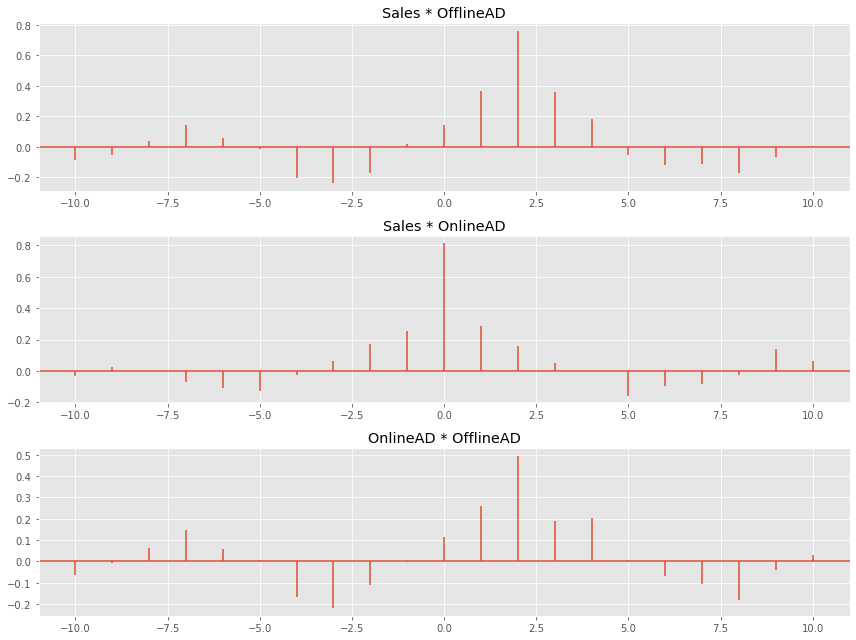
# 相互相関コレログラム
#

fig, ax = plt.subplots(3,1)

# SaleaとOfflioneADの相互相関
ax[0].xcorr(df_std.iloc[:,0], df_std.iloc[:,1])
ax[0].title.set_text(str(df_std.columns[0]+' * '+df_std.columns[1]))

# SaleaとOnlineADの相互相関
ax[1].xcorr(df_std.iloc[:,0], df_std.iloc[:,2])
ax[1].title.set_text(str(df_std.columns[0]+' * '+df_std.columns[2]))

# OnlineADとOfflioneADの相互相関
ax[2].xcorr(df_std.iloc[:,2], df_std.iloc[:,1])
ax[2].title.set_text(str(df_std.columns[2]+' * '+df_std.columns[1]))

fig.tight_layout()
plt.show()

以下、実行結果です。横軸がラグです。

1つ目のコレログラムは、Salesに対するOfflineADのラグとの相関です。

SalesとOfflineADのラグ2の相関が最大、つまりSalesと2日前のOfflineADの相関が最大になっています。

グレンジャー因果性の考え方からすると、OfflineAD→Salesと考えられます。

2つ目のコレログラムは、Salesに対するOnlineADのラグとの相関です。

SalesとOnlineADのラグ0の相関が最大、つまりSalesと同日のOnlineADの相関が最大になっています。

グレンジャー因果性の考え方からすると、判断はつきません。なぜならば、OnlineADの過去の値がSalesの将来の値を予測する能力を有するかどうか分からないからです。

ただ、予測的因果関係という観点で考えると、同時点ではあるもののOnlineAD→Salesと考えられます。

3つ目のコレログラムは、OnlineADに対するOfflineADのラグとの相関です。

OnlineADとOfflineADのラグ2の相関が最大、つまりOnlineADと2日前のOfflineADの相関が最大になっています。

グレンジャー因果性の考え方からすると、OfflineAD→OnlineADと考えられます。

　有向グラフ

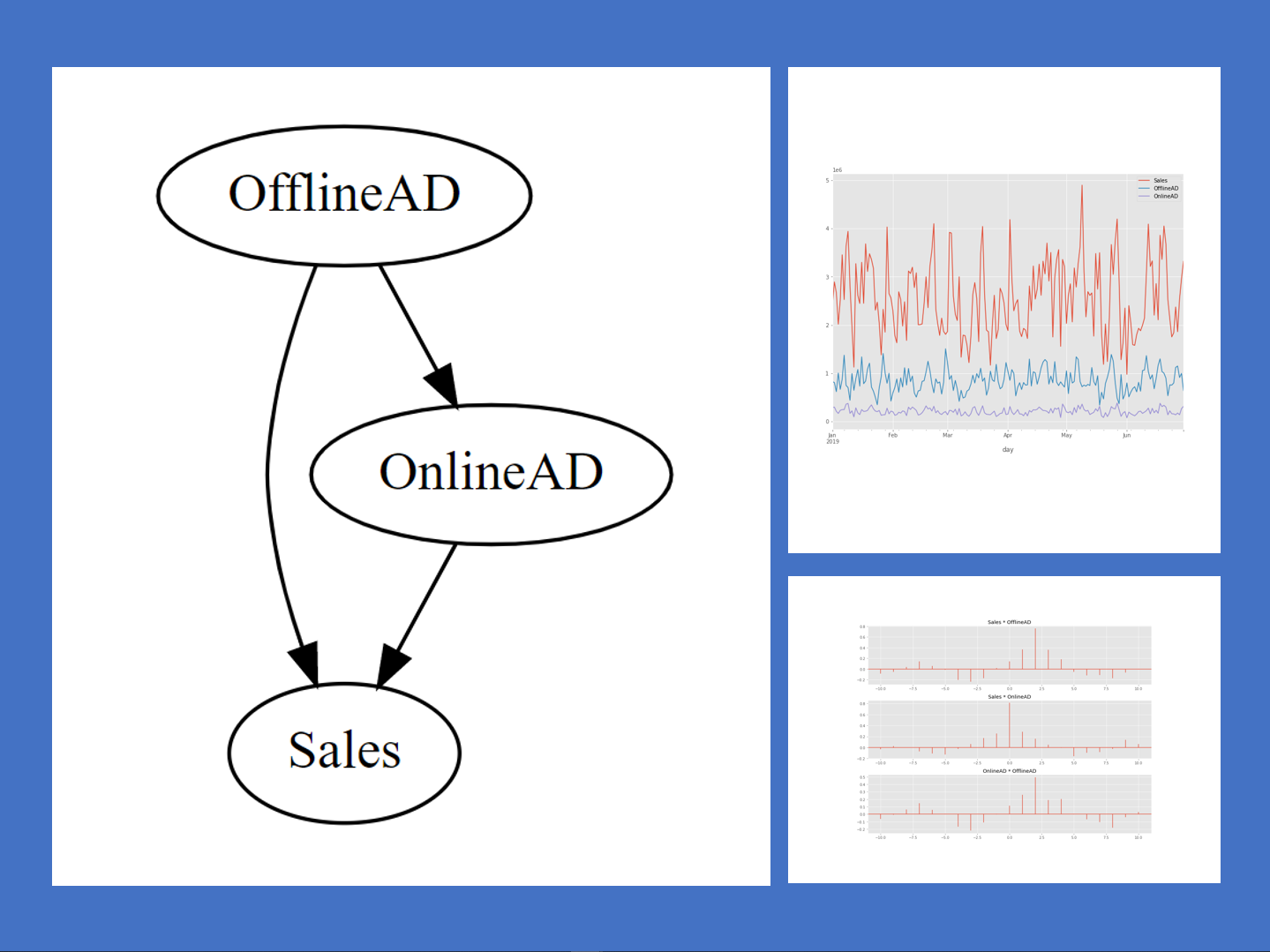
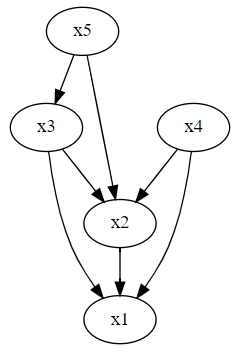
相互相関コレログラムから、次のことが読み取れました。

OfflineAD→Sales
OnlineAD→Sales
OfflineAD→OnlineAD

この関係性を、有向グラフで描いて見ます。

以下、コードです。

#
# 有向グラフ（先行変数＋一致変数）
#

graph = Digraph()

# ノードを追加
for i in range(len(df.columns)):
    graph.node(df.columns[i])

# 辺を追加
graph.edge(df.columns[1], df.columns[0]) #OfflineAD -> Sales
graph.edge(df.columns[1], df.columns[2]) #OfflineAD -> OnlineAD
graph.edge(df.columns[2], df.columns[0]) #OnlineAD -> Sales

# 画像を表示
graph

以下、実行結果です。