最適化問題をPythonのPyomoライブラリーで解こう

その2：線形計画問題（行列とベクトルを利用）

4953
最適化問題をPythonのPyomoライブラリーで解こうその2：線形計画問題（行列とベクトルを利用）

最適化問題は、マーケティング予算配分の最適化、配送ルートの最適化、スケジュール最適化など、何かを最適化する問題を扱うものです。

最適化問題には、登場する数式や最適解の条件などによって、線形計画問題や非線形計画問題、混合整数計画問題などがあります。

基本となるのが、線形計画問題です。線形式しか登場しません。前回、PythonのPyomoライブラリーで解く方法について簡単に説明しました。

最適化問題をPythonのPyomoライブラリーで解こうその1：線形計画問題

 

前回の例で登場した最適化問題は小規模のものでしたが、現実は変数や数式の数は数百、数千、数万になります。

その場合、今回のように1つ1つ数式を定義していくことは現実的ではありません。

例えば、数式の係数や変数の上限や下限の制約を、外部からデータとして取得し、設定することが多いです。

今回は、「行列とベクトルを使った線形計画問題」というお話しをします。前回と同じ最適化問題を扱います。

前回の復習です。

前回の復習

　最適化の構成要素

最適化には3つの構成要素があります。

  • 目的関数
  • 変数
  • 制約条件

「ある制約条件のもと目的関数を最適化（最大化 or 最小化）する変数を見つける」のが最適化問題です。

 

　モデリングツールとソルバー

最適化問題を解くには、次の2つのツールが必要になります。

  • モデリングツール；最適化問題を記述するためのツール
  • ソルバー：記述された最適化問題を計算するためのツール

Pyomoは、モデリングツールです。

GLPK（GNU Linear Programming Kit)は、線形計画問題を解くための無料のソルバーです。

 

　最適化問題のモデリングし解くまでの流れ

以下、最適化問題を解くまでの流れです。

  1. モデリング
    1. モデルのインスタンスの生成
    2. 変数の定義
    3. 目的関数の定義
    4. 制約条件の定義
  2. 最適化
    1. ソルバーの設定
    2. 最適化の実施
  3. 結果確認

非常にシンプルです。

 

最適化する問題（前回と同じ）

今回、最適化する問題です。

\displaystyle<br /> \begin{aligned}<br /> & \underset{x} \text{min} && f(x_1,x_2) = 75 x_1 + 125 x_2 \\<br /> & \text{subject to} && 6x_1 + 3x_2 \ge 38 \\<br /> &&& 5x_1 + 21x_2 \ge 29\\<br /> \end{aligned}<br />

ベクトルや行列で表現すると、以下のようになります。

\displaystyle<br /> \begin{aligned}<br /> & \underset{x} \text{min} && f(\bm{x}) = \bm{\alpha}^T \bm{x} \\<br /> & \text{subject to} && \bm{A x} \ge \bm{\beta} \\<br /> \end{aligned}<br /> \displaystyle<br /> \bm{x}=\begin{bmatrix}<br /> x_1 \\<br /> x_2<br /> \end{bmatrix}、<br /> \bm{\alpha}=\begin{bmatrix}<br /> 75 \\<br /> 125<br /> \end{bmatrix}、<br /> \bm{A}=\begin{bmatrix}<br /> 6 & 3 \\<br /> 5 & 21<br /> \end{bmatrix}、<br /> \bm{\beta}=\begin{bmatrix}<br /> 38 \\<br /> 29<br /> \end{bmatrix}<br />

さらに、変数に幾つかの制約をつけた場合、どうなるのかを見ていきます。

今回は、変数への制約の付け方を、次の3パターンで設定し見ていきます。

  • 変数に非負制約あり
  • 変数に範囲制約あり
  • 変数に整数制約と範囲制約あり

 

前回と異なるところ

目的関数や制約式の係数などを、行列およびベクトル（正確には、NumPyの配列（array））として与えられたとして、前回と同じ最適化問題を解いていきます。

NumPyの配列（array）として与えられたデータを、辞書(dictionary)へ変換し、Pyomoでモデリングします。

 

必要なモジュールの読み込み

先ずは、利用するモジュールを読み込みます。

以下、コードです。

import numpy as np
import pyomo.environ as pyo
from pyomo.opt import SolverFactory

 

データ（目的関数や制約式の係数など）

目的関数や制約式の係数などを、行列およびベクトル（正確には、NumPyの配列（array））として設定し、それを辞書(dictionary)へ変換します。

以下、コードです。

#
# 変数の数
#

I = 2

#
# データ（係数など）
#

## 目的変数の係数
a_data =  np.array([75,125])

## 係数行列
t_data = np.array([[6, 3],
                   [5, 21]])

## ベクトル（各制約式の下限）
t0_data = np.array([38,29])

#
# 辞書(dictionary)へ変換
#

## 目的変数の係数
a = dict((i, a_data[i-1]) for i in range(1, I+1))

## 係数行列
t = dict(
    ((i, j), t_data[i-1][j-1])  
    for i in range(1, I+1) 
    for j in range(1, I+1)
)

## ベクトル（各制約式の下限）
t0 = dict((i, t0_data[i-1]) for i in range(1,I+1))

 

最適解の計算

　変数に制約なし

先ず、モデリングです。

モデルのインスタンスを生成します。

以下、コードです。

model = pyo.ConcreteModel()

 

変数を定義します。2要素のベクトルxです。

以下、コードです。

# 添字
model.I = pyo.Set(initialize=range(1, I+1))

# 変数
model.x = pyo.Var(model.I, within=pyo.Reals)

 

次の目的関数を定義します。

\displaystyle<br /> \begin{aligned}<br /> && f(x_1,x_2) = 75 x_1 + 125 x_2<br /> \end{aligned}<br />

目的関数を数式として表現し関数として定義した後に、その関数を目的関数に設定します。

以下、コードです。

# 目的関数の数式の定義
def ObjRule(model):
    return sum(a[i] * model.x[i] for i in model.I)

# 目的関数として設定
model.obj = pyo.Objective(rule = ObjRule,
                          sense = pyo.minimize)

 

次の2つの制約条件を定義します。

\displaystyle<br /> \begin{aligned}<br /> &&& 6x_1 + 3x_2 \ge 38 \\<br /> &&& 5x_1 + 21x_2 \ge 29\\<br /> \end{aligned}<br />

制約条件を数式として表現し関数として定義した後に、その関数を制約条件に設定します。

以下、コードです。

# 制約条件の数式の定義
def Construle(model, i):
    return sum(t[i,j] * model.x[j] for j in model.I) >= t0[i]

# 制約条件として設定
model.eq = pyo.Constraint(model.I, rule = Construle)

 

モデリングが終了したので、ソルバーを設定し最適化します。

以下、コードです。

# 最適化

## ソルバーの設定
opt = pyo.SolverFactory('glpk')

## 最適化の実施
res = opt.solve(model)

 

結果を確認します。

以下、コードです。

print(model.display())
print('\n')
print('optimum value = ', model.obj())
print("x = ", model.x[:]())

 

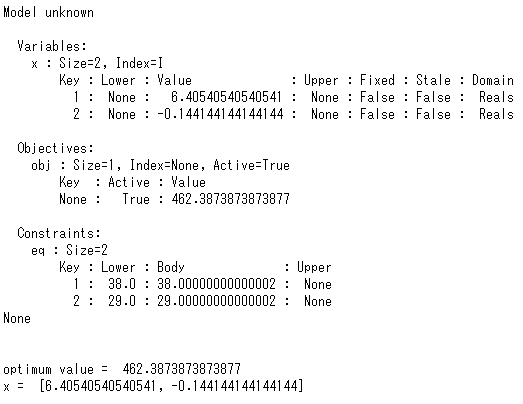
以下、実行結果です。

 

最適解は……

\displaystyle<br /> \begin{aligned}<br /> &&& x_1 = 6.40540540540541\\<br /> &&& x_2 = -0.144144144144144\\<br /> \end{aligned}<br />

最適値（最小値）は……

\displaystyle<br /> \begin{aligned}<br /> && f(x_1,x_2) = 462.3873873873877<br /> \end{aligned}<br />

 

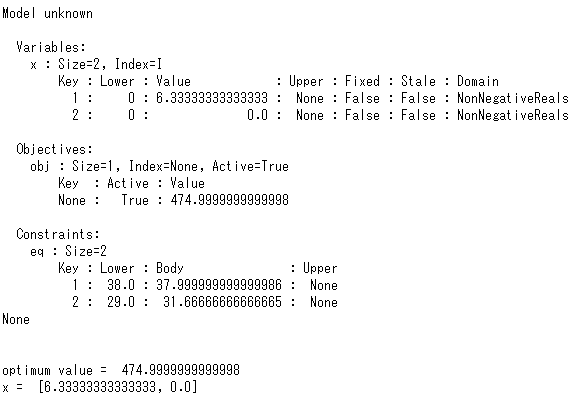
　変数に非負制約あり

変数に非負制約をつけた場合です。

#
# モデルのインスタンスの生成
#

model = pyo.ConcreteModel()

#
# 変数の定義
#

# 添字
model.I = pyo.Set(initialize=range(1, I+1))

# 変数
model.x = pyo.Var(model.I, domain=pyo.NonNegativeReals)

#
# 目的関数
#

# 目的関数の数式の定義
def ObjRule(model):
    return sum(a[i] * model.x[i] for i in model.I)

# 目的関数として設定
model.obj = pyo.Objective(rule = ObjRule,
                          sense = pyo.minimize)

#
# 制約条件
#

# 制約条件の数式の定義
def Construle(model, i):
    return sum(t[i,j] * model.x[j] for j in model.I) >= t0[i]

# 制約条件として設定
model.eq1 = pyo.Constraint(model.I, rule = Construle)

#
# 最適化
#

# ソルバーの設定
opt = SolverFactory('glpk')

# 最適化の実施
res = opt.solve(model)

#
# 結果確認
#

print(model.display())
print('\n')
print('optimum value = ', model.obj())
print("x = ", model.x[:]())

 

以下、コードです。

以下、実行結果です。

 

　変数に範囲制約あり

変数の上限と下限のベクトルを設定します。こちらも、ベクトル（正確には、NumPyの配列（array））として設定し、それを辞書(dictionary)へ変換します。

以下、コードです。

#
# 上限と下限のデータの追加
#

# データ（係数など）

## 変数の上限
upper_data = np.array([5,10])

## 変数の下限
lower_data = np.array([-5,0])

# 辞書(dictionary)へ変換

## 変数の上限
upper = dict((i, upper_data[i-1]) for i in range(1,I+1))

## 変数の下限
lower = dict((i, lower_data[i-1]) for i in range(1,I+1))

 

変数に範囲制約をつけた場合の、最適化モデルの生成と実行です。

以下、コードです。

#
# モデルのインスタンスの生成
#

model = pyo.ConcreteModel()

#
# 変数の定義
#

# 添字
model.I = pyo.Set(initialize=range(1, I+1))

# 変数
model.x = pyo.Var(model.I, domain=pyo.NonNegativeReals)

#
# 目的関数
#

# 目的関数の数式の定義
def ObjRule(model):
    return sum(a[i] * model.x[i] for i in model.I)

# 目的関数として設定
model.obj = pyo.Objective(rule = ObjRule,
                          sense = pyo.minimize)

#
# 制約条件
#

# 制約1
def Construle1(model, i):
    return sum(t[i,j] * model.x[j] for j in model.I) >= t0[i]

model.eq1 = pyo.Constraint(model.I, rule = Construle1)

# 制約2
def Construle2(model, i):
    return model.x[i] <= upper[i]

model.eq2 = pyo.Constraint(model.I, rule = Construle2)

# 制約3
def Construle3(model, i):
    return model.x[i] >= lower[i]

model.eq3 = pyo.Constraint(model.I, rule = Construle3)

#
# 最適化
#

# ソルバーの設定
opt = SolverFactory('glpk')

# 最適化の実施
res = opt.solve(model)

#
# 結果確認
#

print(model.display())
print('\n')
print('optimum value = ', model.obj())
print("x = ", model.x[:]())

 

以下、実行結果です。

 

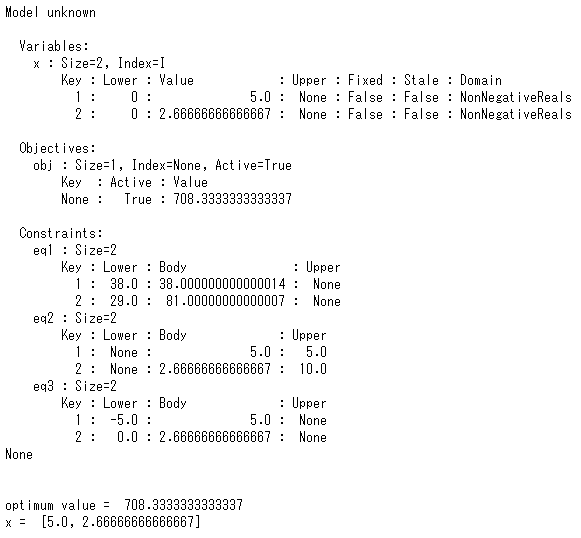
　変数に整数制約と範囲制約あり

変数に整数制約と範囲制約をつけた場合です。

以下、コードです。

#
# モデルのインスタンスの生成
#

model = pyo.ConcreteModel()

#
# 変数の定義
#

# 添字
model.I = pyo.Set(initialize=range(1, I+1))

# 変数
model.x = pyo.Var(model.I, domain=pyo.Integers)

#
# 目的関数
#

# 目的関数の数式の定義
def ObjRule(model):
    return sum(a[i] * model.x[i] for i in model.I)

# 目的関数として設定
model.obj = pyo.Objective(rule = ObjRule,
                          sense = pyo.minimize)

#
# 制約条件
#

# 制約1
def Construle1(model, i):
    return sum(t[i,j] * model.x[j] for j in model.I) >= t0[i]

model.eq1 = pyo.Constraint(model.I, rule = Construle1)

# 制約2
def Construle2(model, i):
    return model.x[i] <= upper[i]

model.eq2 = pyo.Constraint(model.I, rule = Construle2)

# 制約3
def Construle3(model, i):
    return model.x[i] >= lower[i]

model.eq3 = pyo.Constraint(model.I, rule = Construle3)

#
# 最適化
#

# ソルバーの設定
opt = SolverFactory('glpk')

# 最適化の実施
res = opt.solve(model)

#
# 結果確認
#

print(model.display())
print('\n')
print('optimum value = ', model.obj())
print("x = ", model.x[:]())

 

以下、実行結果です。

 

まとめ

今回は、「行列とベクトルを使った線形計画問題」というお話しをしました。

前回と同じ、線形の最適化問題を扱いました。

しかし、ビジネス上の問題を定式化したとき、常に線形式で表現されるものではなく、非線形で表現されるケースの方が多いです。

次回は、「非線形計画問題」というお話しをします。

最適化問題をPythonのPyomoライブラリーで解こうその3：非線形計画問題