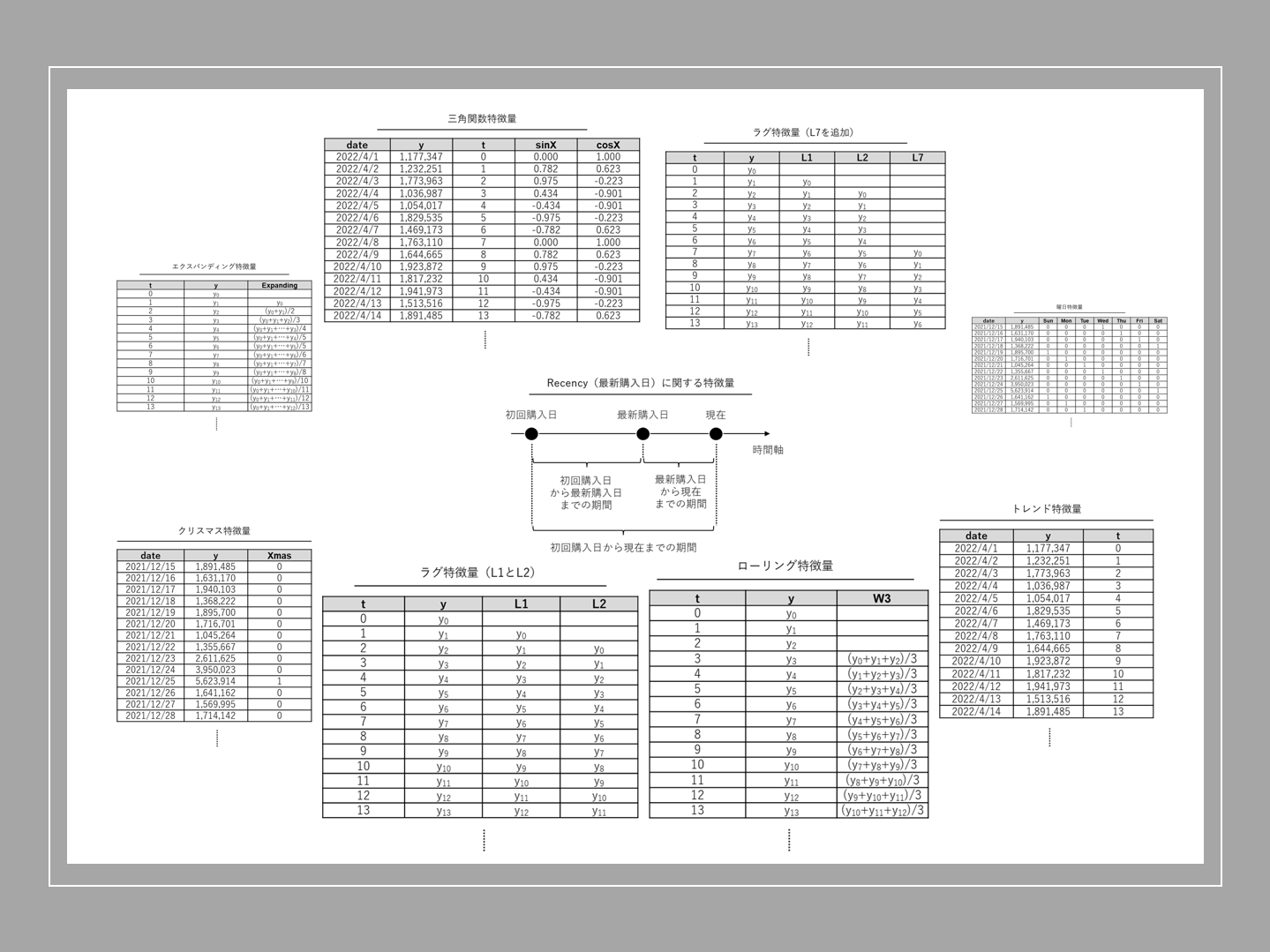
時系列データのデータセットには、時間変数や指標変数、層別変数の他にも変数があります。時間や指標、層別などの特徴を表す変数です。「特徴量」と言ったりします。
例えば、休日かどうかを表す変数であったり、過去1周間の平均売上を表す変数であったり、顧客の属性を表す変数であったり、色々な特徴量が考えられます。
特徴量は、時系列データのデータセットにだけに存在するものではなく、通常のテーブルデータのデータセットなどにも存在します。
ただ、時系列ならではの特徴量が幾つかあります。
例えば、次の7つの特徴量です。ここでは、時系列特徴量と呼ぶことにします。他にも色々あるかもしれませんが、この7つを紹介します。
- トレンド特徴量
- 三角関数特徴量
- ドメイン固有カレンダー特徴量
- ラグ特徴量
- ローリング特徴量
- エクスパンディング特徴量
- RFM特徴量
今回は、言葉だけだとイメージが付きにくいので、それぞれ簡単に説明していきます。
トレンド特徴量
トレンド特徴量とは、トレンド成分を表現するための特徴量で、最もシンプルなものは次のような「0,1,2,…」と連番の特徴量(例では、変数名はt)です。
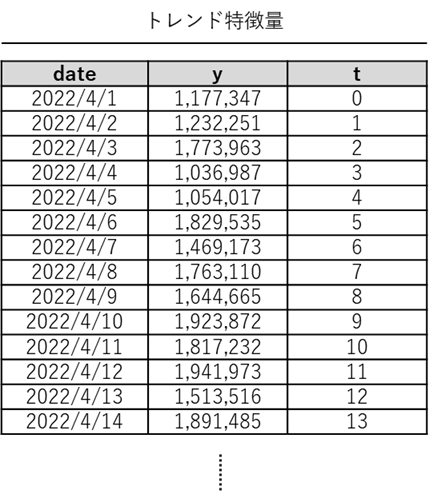
線形のトレンドを表現するのであれば、この連番の特徴量だけで十分です。利用するときは、この連番の特徴量を説明変数Xの1つとして利用します。
2次式や3次式にするのであれば、この変数tを2乗や3乗した変数を作ります。
トレンドを表現する方法は他にもあります。例えば、後ほど登場するローリング特徴量やエクスパディング特徴量です。
三角関数特徴量
季節性の表現方法には幾つか種類があります。その1つが、フーリエ級数に基づくsinやcosといった三角関数を利用した表現方法です。
今、時系列データ y_tがあったとします。
考慮したい季節性が M個、各季節性の周期がp_i(i=1,2,\dots,M)、各季節性のフーリエ項がK_i個 、N_tが季節性以外の時系列成分とします。aは定数項、\alpha_ik,\beta_ikは係数で、学習し求めるパラメータです。
次のように表現できます。
\displaystyle y_t=a+\sum_{i=1}^{M}\sum_{k=1}^{K_i}\left[\alpha_{ik}\sin{\left(\frac{2\ \pi\ k\ t}{p_i}\right)+\beta_{ik}\cos{\left(\frac{2\ \pi\ k\ t}{p_i}\right)}}\right]+N_t数式を見ると若干複雑そうに見えますが、作り方が明確なので機械的に特徴量を作ることができます。
季節性が1つ(M=1)でフーリエ項が1セット(K_1=1)のシンプルな場合、その季節性はcosとsinの2変数で表現されます。pは周期です。
\displaystyle y_t=a+\alpha\sin{\left(\frac{2\pi t}{p}\right)+\beta\cos{\left(\frac{2\ \pi t}{p}\right)}}+N_tこのとき、各三角関数特徴量(例では、変数名はsinXとcosX)の値は、t=1,2,\dotsに対しsinX_t=\sin{\left(\frac{2\ \pi t}{p}\right)}\ 、cosX_t=\cos{\left(\frac{2\ \pi t}{p}\right)}で求めます。

そう考えると、sinとcosのセットを増やせばいいのではとなりますが、無駄に変数が多くなります。
そこで、「sinとcosを何セット必要なのか(K_iをどう決めるか)」という問題があります。
ちなみに、後ほど登場するドメイン固有カレンダー特徴量やラグ特徴量でも季節性を表現することができます。
ドメイン固有カレンダー特徴量
ドメイン固有カレンダー特徴量とは、カレンダー情報に紐づいた業界特有の特徴量やその企業固有の特徴量です。
ドメイン固有カレンダー特徴量の最も簡単な特徴量の作り方は、フラグ変数(0-1変数)を作る方法です。
例えば、クリスマスに売上が跳ね上がる業界であれば、クリスマスを表すフラグ変数(例では、変数名はXmas)を1つ作り、12/25に「1」を、それ以外の日に「0」と入力します。
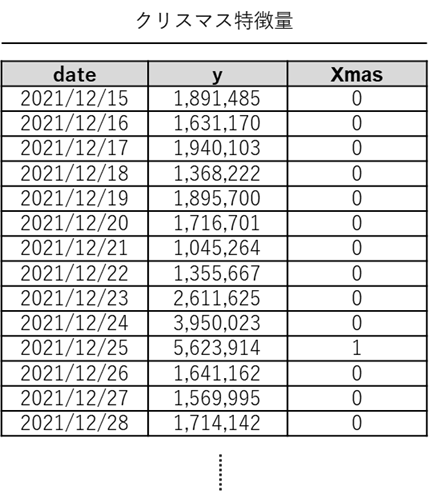
クリスマスイブやクリスマス数日前から売上が跳ね上がる場合には、12/23や12/24などを表すフラグ変数(0-1変数)を個別に作るか、クリスマスを表すフラグ変数(0-1変数)をそのまま12/23や12/24などでも利用するか、など幾つか方法があります。
他には、年に数回のイベントなどだけでなく、年に何度も定期的に訪れるものも、ドメイン固有カレンダー特徴量として表現できます。
例えば、曜日、休日、大型連休の初日、年度初め、などを表現する特徴量を設けることがあります。このような特徴量は、念のため変数として準備しておいたほうがいいでしょう。
こちらも、例えば次のようにフラグ変数で表現するケースが多いです。

曜日などの一定の周期のあるものであれば、先ほど紹介した三角関数特徴量や、次に登場するラグ特徴量で表現することもできます。
ラグ特徴量
「ラグ特徴量」は、最も一般的な時系列特徴量です。
元の時系列データを、1期や2期などずらして作った特徴量で、1期ずらすことをラグ1、2期ずらすことをラグ2と言ったりします。
今、ある小売店の日単位の売上データy_tがあったとします。
t期(今回の例では日)の売上y_tに対応する、ラグ1の「ラグ特徴量」(例では、変数名はL1)の値はt-1期の売上(前日の売上)y_{t-1}です。ラグ2の「ラグ特徴量」(例では、変数名はL2)の値はt-2期の売上(前々日の売上)y_{t-2}です。
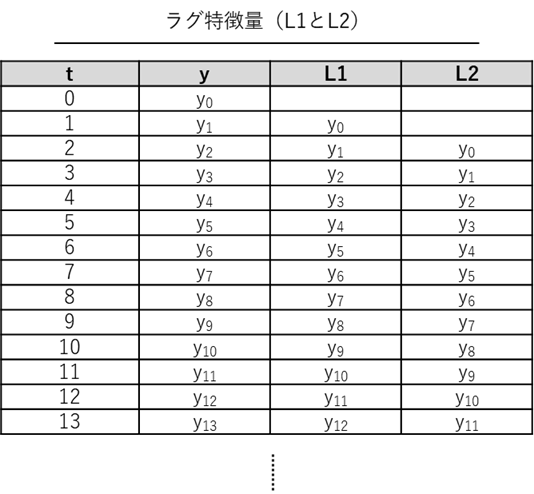
多くの小売店には、売上データy_tに7日間周期の季節性があります。このような場合、ラグ7の「ラグ特徴量」(例では、変数名はL7)を作り予測に利用するだけで、それなりの精度の予測モデルを構築できます。
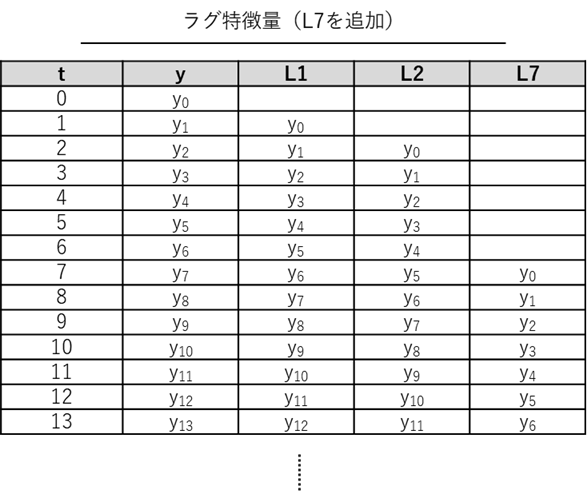
「ラグ特徴量」を作ると、データセットの先頭の幾つかが欠測値(データが無い状態)になります。
例では、変数L1、L2,L7の2022/4/1の行に欠測値があります。2022/4/1の前日である2022/3/31のデータが、元のデータセットに無いためです。
ローリング特徴量
ローリング特徴量も、それなりによく作成される時系列特徴量です。
ローリング特徴量とは、過去の一定期間(Rolling Window)の平均値や合計値などの集計値です。
今、月単位の売上データy_tがあったとします。
例えば、t期(今回は例ではt月)の売上y_tの、3ヶ月間平均の「ローリング特徴量」(例では、変数名はW3)の値は、t-3,t-2,t-1の3期の売上の平均値\left(y_{t-3}+y_{t-2}+y_{t-1}\right)/3となります。
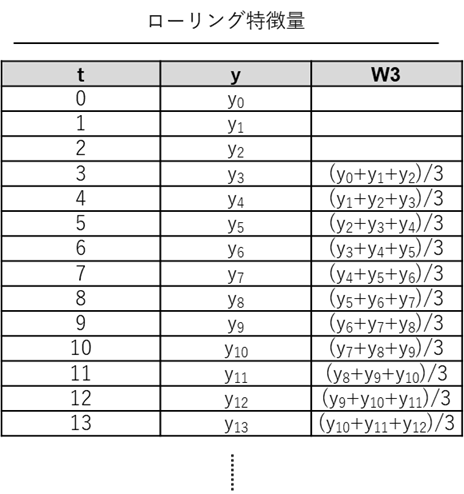
ローリング特徴量は、「移動〇〇」と呼ばれることもあります。今の例の場合、「移動平均」と呼ばれます。
平均値ではなく、最大値や最小値、標準偏差、分散などでも構いません。
エクスパンディング特徴量
エクスパンディング特徴量とは、過去すべての期間(Expanding Window)の集計値を特徴量としたものです。
ローリング特徴量と似ていますが、集計対象となる過去の期間が異なります。
エクスパンディング特徴量は過去全期間で、ローリング特徴量は決められた一定期間です。
今、月単位の売上データy_tがあったとします。
例えば、t期(今回は例では 月)の売上y_tの、前期までの全過去平均値の「エクスパディング特徴量」(例では、変数名はExpanding)の値は\sum_{i=0}^{t-1}y_i/tです。
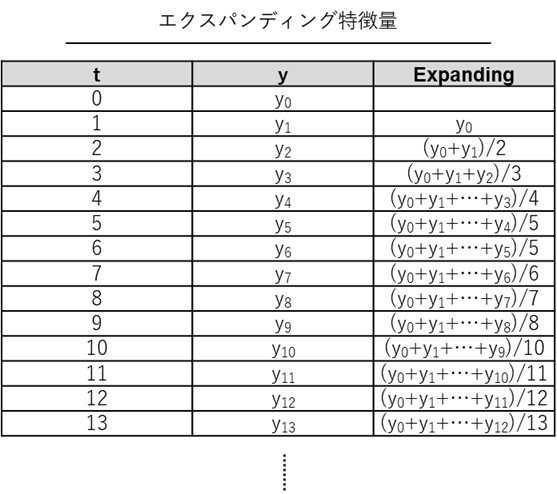
平均値ではなく、最大値や最小値、標準偏差、分散などでも構いません。
RFM特徴量
RFMとは、マーケティングの顧客購買分析でよく用いられる分析の切り口の1つで、次の3つの頭文字をとったものです。
- Recency:最新購入日
- Frequency:購入回数
- Monetary:累計金額
最新購入日に関しては、例えば次の2つの特徴量が作れます。
- 初回購入日から最新購入日までの期間
- 最新購入日から現在までの期間
この2つの期間を合計すると、初回購入日から現在までの期間となり、それも特徴量としてもいいでしょう。

購入回数と累計金額に関しては、ローリング特徴量とエクスパンディング特徴量と密接な関係にあります。
例えば、過去1年間の「購入回数」は、過去1年間の「購入した回数を合計し求めたローリング特徴量」です。今までの累計金額は、今までの「取引金額すべてを合計し求めたエクスパンディング特徴量」です。
購買データに限らず、どのような時系列特徴量を作ればいいのか迷ったとき、このRFMの3つの視点を参考に、ローリング特徴量とエクスパンディング特徴量などを作るのも手です。
例えば、見込み顧客(リード)の受注予測をする予測モデルを構築するとき、直近のコンタクトからの経過日数や商談開始からの経過日数、ここ3カ月間の商談回数や提案金額累計などが特徴量として利用できるかもしれません。これらは全てRFM特徴量です。
今回のまとめ
今回は、「時系列特徴量7選」についてお話しをしました。
時系列データのデータセットには、時間変数や指標変数、層別変数の他にも変数があります。時間や指標、層別などの特徴を表す変数です。「特徴量」と言ったりします。
例えば、休日かどうかを表す変数であったり、過去1周間の平均売上を表す変数であったり、顧客の属性を表す変数であったり、色々な特徴量が考えられます。
特徴量は、時系列データのデータセットにだけに存在するものではなく、通常のテーブルデータのデータセットなどにも存在します。
ただ、時系列ならではの特徴量が幾つかあります。
例えば、次の7つの特徴量です。ここでは、時系列特徴量と呼ぶことにします。他にも色々あるかもしれませんが、この7つを紹介します。
- トレンド特徴量
- 三角関数特徴量
- ドメイン固有カレンダー特徴量
- ラグ特徴量
- ローリング特徴量
- エクスパンディング特徴量
- RFM特徴量
時系列データを分析するときなど、参考にしていただければと思います。