StatsForecastは、色々な統計学的な時系列系の予測モデルを構築することのできる、Pythonの時系列予測パッケージです。
以前、StatsForecastのインストール方法から簡単な使い方(予測モデル構築とテストなど)を説明しました。
StatsForecastは、複数の時系列予測モデルを作れるということで、時系列アンサンブル学習に最適です。
アンサンブル学習とは、複数の予測モデルを組み合わせ予測するための、予測モデルを構築する学習アプローチです。
今回は、「StatsForecast で時系列アンサンブル学習による予測」というお話しです。
Contents [hide]
今回実施するアンサンブル学習
今回は、次の2種類の時系列のアンサンブル学習を実施し、予測モデルを構築していきます。
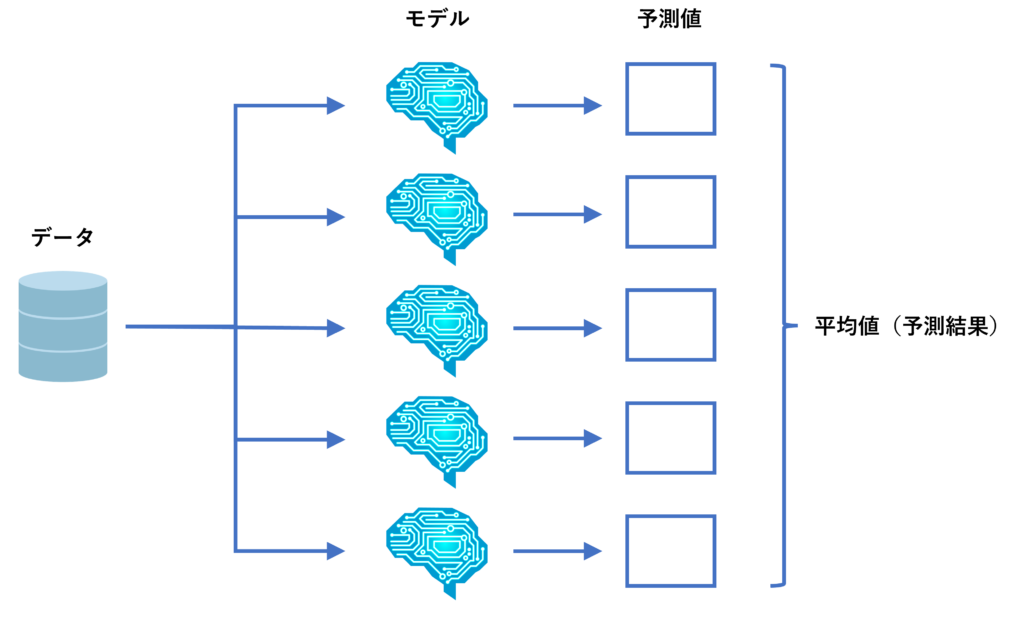
- アンサンブル(平均値)
- アンサンブル(重回帰)
アンサンブル(平均値)は、複数の予測モデルを学習し、その予測結果の平均値を計算しそれを最終的な予測結果にするアプローチです。
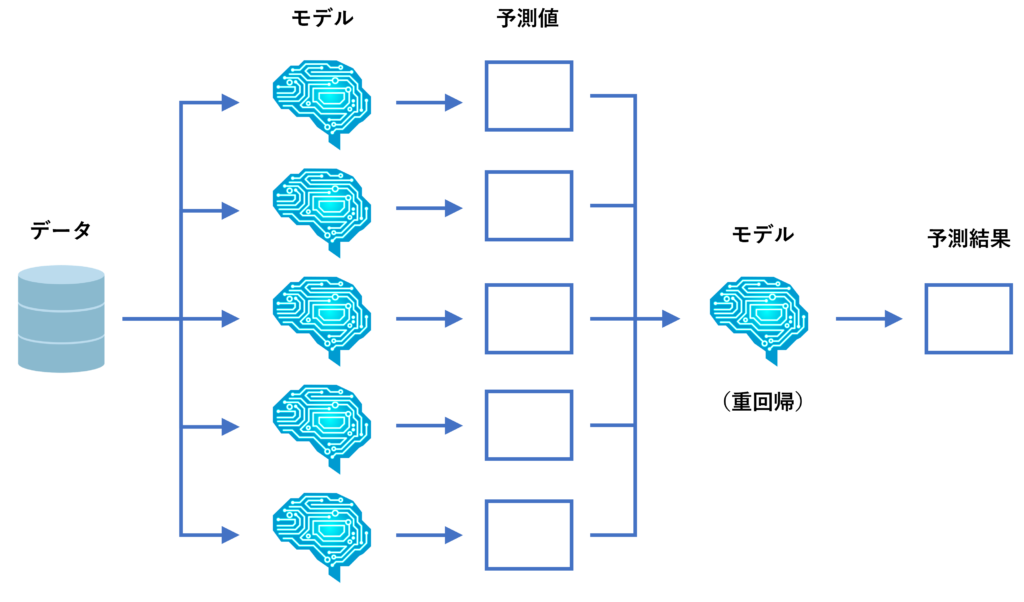
アンサンブル(重回帰)は、複数の予測モデルを学習し、その予測値を特徴量(説明変数)とした予測モデルを、重回帰モデルで学習しその予測値を最終的な予測結果とするアプローチです。
ちなみに、アンサンブル学習で高精度な予測モデルが構築できる保証はありません。悪化することもあります。
今回利用するデータ
次の2つのデータセットを利用します。
- AirPassengers(飛行機乗客数)
- WineSales(ワイン販売数)
AirPassengers(飛行機乗客数)は、Box&Jenkinsの有名なデータで、1949年から1960年までの国際線航空旅客数の月次集計結果です。
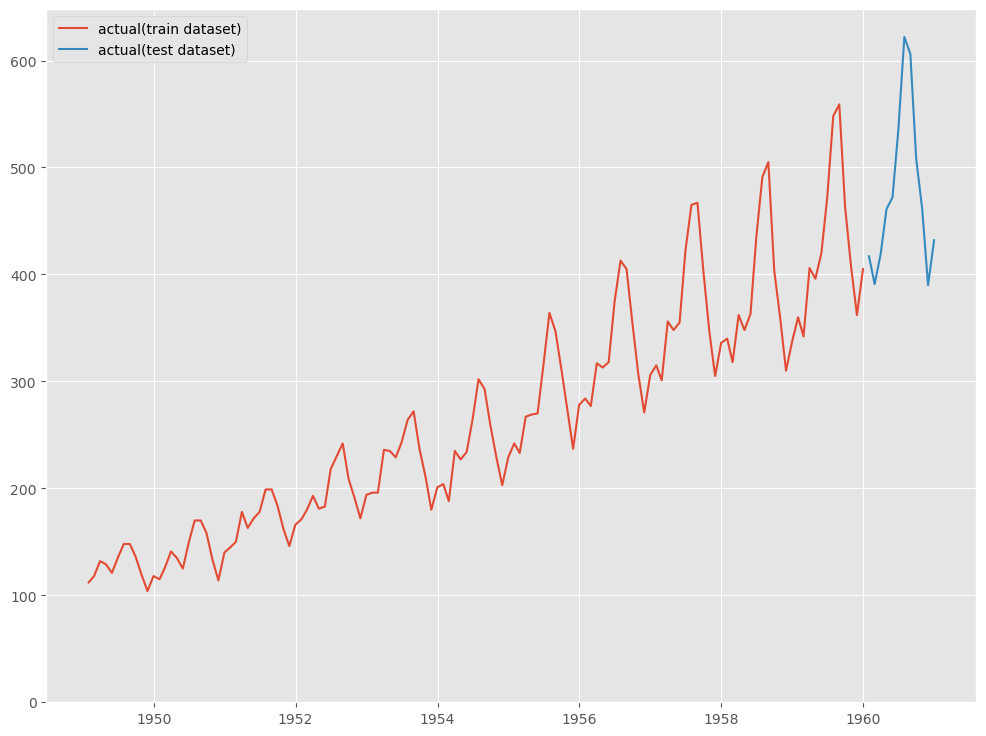
StatsForecastが、サンプルデータとして提供しているため、それをそのまま使います。
WineSales(ワイン販売数)は、R forecast パッケージに含まれている1980年1月~1994年8月までのワイン販売数の月次集計結果です。
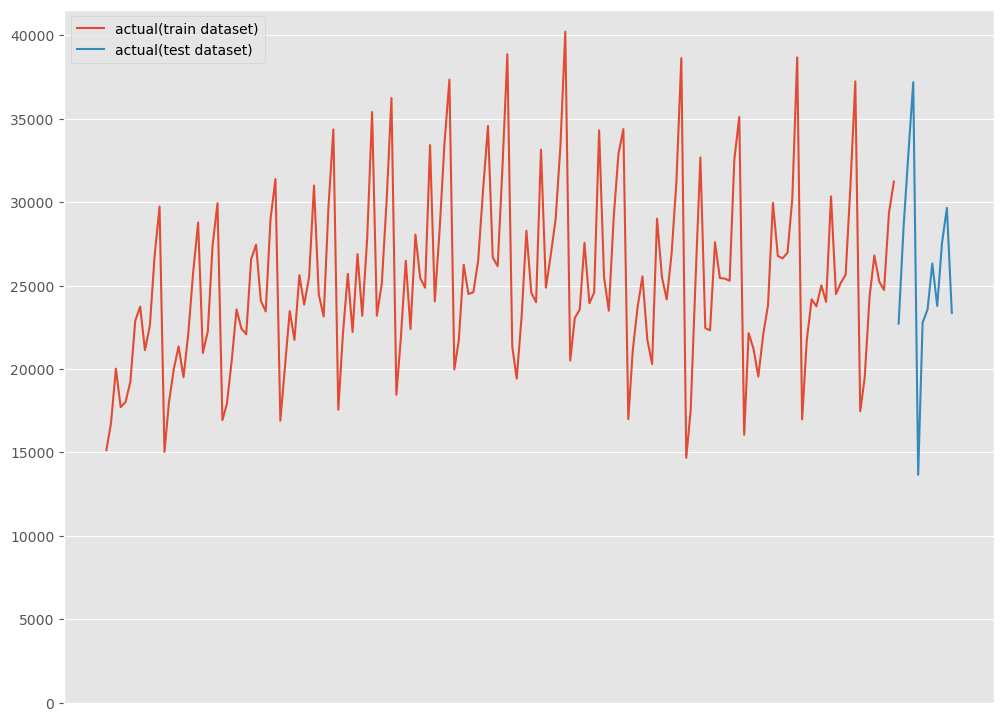
Rで提供されているサンプルデータは、statsmodelsのモジュールを使うことでPythonに読み込むことができます。詳細は以下の記事を参考にしてください。
予測精度の評価指標
今回利用する予測精度の評価指標は、RMSE(二乗平均平方根誤差、Root Mean Squared Error)とMAE(平均絶対誤差、Mean Absolute Error)、MAPE(平均絶対パーセント誤差、Mean absolute percentage error)の3つです。
以下の記号を使い精度指標の説明をします。
■ 二乗平均平方根誤差(RMSE、Root Mean Squared Error)
■ 平均絶対誤差(MAE、Mean Absolute Error)
■ 平均絶対パーセント誤差(MAPE、Mean absolute percentage error)
必要なモジュールの読み込み
先ず、利用するモジュールを読み込みます。
以下、コードです。
#
# 必要なモジュールの読み込み
#
import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsforecast import StatsForecast
from statsforecast.models import (
AutoARIMA,
HoltWinters,
AutoTheta,
AutoETS,
DynamicOptimizedTheta as DOT,
SeasonalNaive
)
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定
では、データセットごとに実施していきます。
AirPassengers(飛行機乗客数)
データの読み込み
データセットを読み込みます。
以下、コードです。
# # データの読み込み # from statsforecast.utils import AirPassengersDF df = AirPassengersDF print(df) #確認
以下、実行結果です。
unique_id ds y 0 1.0 1949-01-31 112.0 1 1.0 1949-02-28 118.0 2 1.0 1949-03-31 132.0 3 1.0 1949-04-30 129.0 4 1.0 1949-05-31 121.0 .. ... ... ... 139 1.0 1960-08-31 606.0 140 1.0 1960-09-30 508.0 141 1.0 1960-10-31 461.0 142 1.0 1960-11-30 390.0 143 1.0 1960-12-31 432.0 [144 rows x 3 columns]
学習データとテストデータ(直近12カ月間)へ分割します。
以下、コードです。
# # 学習データとテストデータ(直近12ヶ月間)へ分割 # # 学習データ df_train = df[:-12] # テストデータ df_test = df[-12:]
学習データを確認してみます。
以下、コードです。
# 学習データの確認 print(df_train)
以下、実行結果です。
unique_id ds y 0 1.0 1949-01-31 112.0 1 1.0 1949-02-28 118.0 2 1.0 1949-03-31 132.0 3 1.0 1949-04-30 129.0 4 1.0 1949-05-31 121.0 .. ... ... ... 127 1.0 1959-08-31 559.0 128 1.0 1959-09-30 463.0 129 1.0 1959-10-31 407.0 130 1.0 1959-11-30 362.0 131 1.0 1959-12-31 405.0 [132 rows x 3 columns]
テストデータを確認してみます。
以下、コードです。
# テストデータの確認 print(df_test)
以下、実行結果です。
unique_id ds y 132 1.0 1960-01-31 417.0 133 1.0 1960-02-29 391.0 134 1.0 1960-03-31 419.0 135 1.0 1960-04-30 461.0 136 1.0 1960-05-31 472.0 137 1.0 1960-06-30 535.0 138 1.0 1960-07-31 622.0 139 1.0 1960-08-31 606.0 140 1.0 1960-09-30 508.0 141 1.0 1960-10-31 461.0 142 1.0 1960-11-30 390.0 143 1.0 1960-12-31 432.0
グラフ化し確認してみます。
以下、コードです。
# グラフ化 fig, ax = plt.subplots() ax.plot(df_train.ds, df_train.y, label="actual(train dataset)") ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。

複数モデルの構築
先ず、複数の予測モデルを構築していきます。
そのために、構築する予測モデルのアルゴリズムのリスト(モデルリスト)を作成します。
以下、コードです。
#
# モデルリストの作成
#
PERIOD = 12
models = [
AutoARIMA(season_length=PERIOD),
HoltWinters(season_length=PERIOD),
SeasonalNaive(season_length=PERIOD),
AutoTheta(season_length=PERIOD),
DOT(season_length=PERIOD),
AutoETS(season_length=PERIOD),
]
学習します。
以下、コードです。
#
# 時系列予測モデルの学習
#
# インスタンス生成
sf = StatsForecast(
models = models,
freq = 'M',
n_jobs=-1,
)
# 学習(学習データ)
sf.fit(df_train)
予測を実施します。
以下、コードです。
# # 予測の実施 # # テストデータ期間 test_pred = sf.forecast(len(df_test),fitted=True) # 学習データ期間 train_pred = sf.forecast_fitted_values()
テストデータ期間の予測結果を確認します。
以下、コードです。
# テストデータの予測結果の確認 print(test_pred)
以下、実行結果です。
ds AutoARIMA HoltWinters SeasonalNaive AutoTheta \
unique_id
1.0 1960-01-31 424.160156 409.680145 360.0 412.711884
1.0 1960-02-29 407.081696 390.044067 342.0 404.640472
1.0 1960-03-31 470.860535 448.929810 406.0 466.810883
1.0 1960-04-30 460.913605 435.445007 396.0 449.600372
1.0 1960-05-31 484.900879 454.699951 420.0 454.047760
1.0 1960-06-30 536.903931 507.904968 472.0 517.857727
1.0 1960-07-31 612.903198 577.622375 548.0 572.380127
1.0 1960-08-31 623.903381 581.996765 559.0 571.371643
1.0 1960-09-30 527.903320 479.946136 463.0 502.108032
1.0 1960-10-31 471.903320 421.522797 407.0 438.527100
1.0 1960-11-30 426.903320 373.590912 362.0 382.673859
1.0 1960-12-31 469.903320 410.594971 405.0 432.116119
DynamicOptimizedTheta AutoETS
unique_id
1.0 412.697632 406.651276
1.0 404.638550 401.732910
1.0 466.829071 456.289642
1.0 449.643433 440.870514
1.0 454.122589 440.333923
1.0 517.984802 496.866058
1.0 572.572754 545.839111
1.0 571.621704 544.672485
1.0 502.383270 477.034485
1.0 438.819733 412.423096
1.0 382.977936 357.949158
1.0 432.517731 402.032745
テストデータ期間の予測精度を見てみます。
以下、コードです。
#
# 精度指標(テストデータ)
#
for i in range(1,7) :
print(test_pred.columns[i])
print('\t'+'RMSE:'+'\t',
np.sqrt(mean_squared_error(df_test.y, test_pred.iloc[:,i])))
print('\t'+'MAE:'+'\t',
mean_absolute_error(df_test.y, test_pred.iloc[:,i]))
print('\t'+'MAPE:'+'\t',
mean_absolute_percentage_error(df_test.y, test_pred.iloc[:,i]))
以下、実行結果です。
AutoARIMA RMSE: 23.955328353374384 MAE: 18.550587972005207 MAPE: 0.04187615687144095 HoltWinters RMSE: 26.228497232379365 MAE: 23.490142822265625 MAPE: 0.048133214753029695 SeasonalNaive RMSE: 50.708316214732804 MAE: 47.833333333333336 MAPE: 0.09987532920823484 AutoTheta RMSE: 24.985179187610136 MAE: 19.35741424560547 MAPE: 0.03919984010285481 DynamicOptimizedTheta RMSE: 24.880112665705433 MAE: 19.263458251953125 MAPE: 0.03901936142148623 AutoETS RMSE: 40.08362053821043 MAE: 35.612475077311196 MAPE: 0.07206839292461678
グラフ化し見てみます。
以下、コードです。
# # グラフ化 # # グラフ用データ(学習データにテストデータ期間の予測結果を結合) pred = pd.concat([df_train,test_pred]).drop(['y','unique_id','ds'], axis=1) pred.index = df.ds # グラフ描写 fig, ax = plt.subplots() ax.plot(df_train.ds, df_train.y, label="actual(train dataset)") ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") pred.plot(ax=ax, linestyle="dotted", lw=2) ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
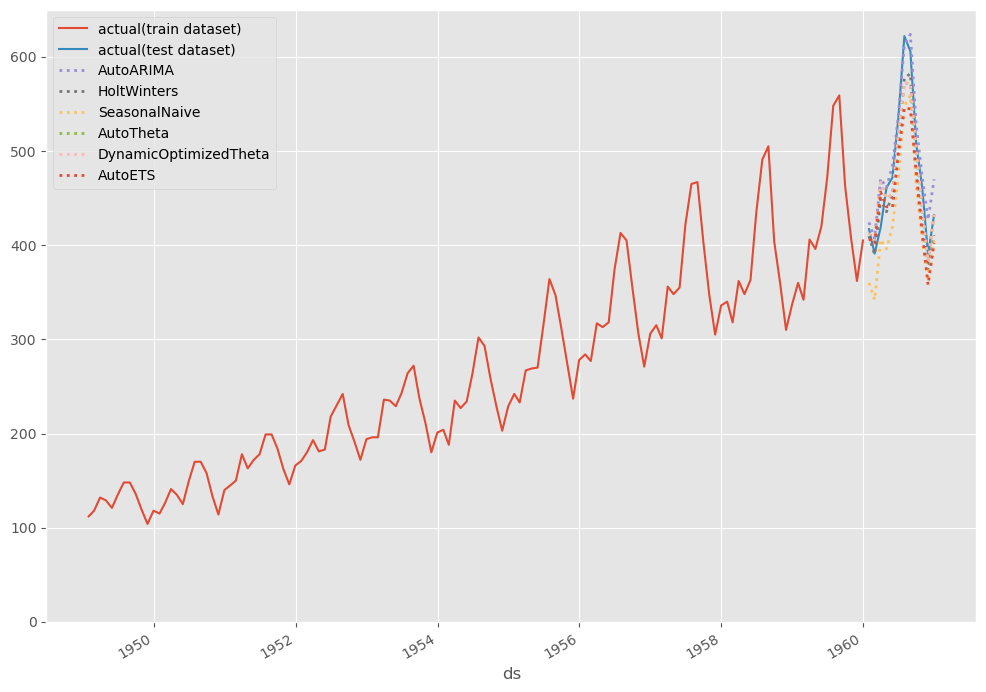
テストデータ期間のみ見てみます。
以下、コードです。
# # グラフ化 # # グラフ用データ(テストデータ期間のみ抽出) pred_test = pred[-12:] # グラフ描写 fig, ax = plt.subplots() ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") pred_test.plot(ax=ax, linestyle="dotted", lw=2) ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
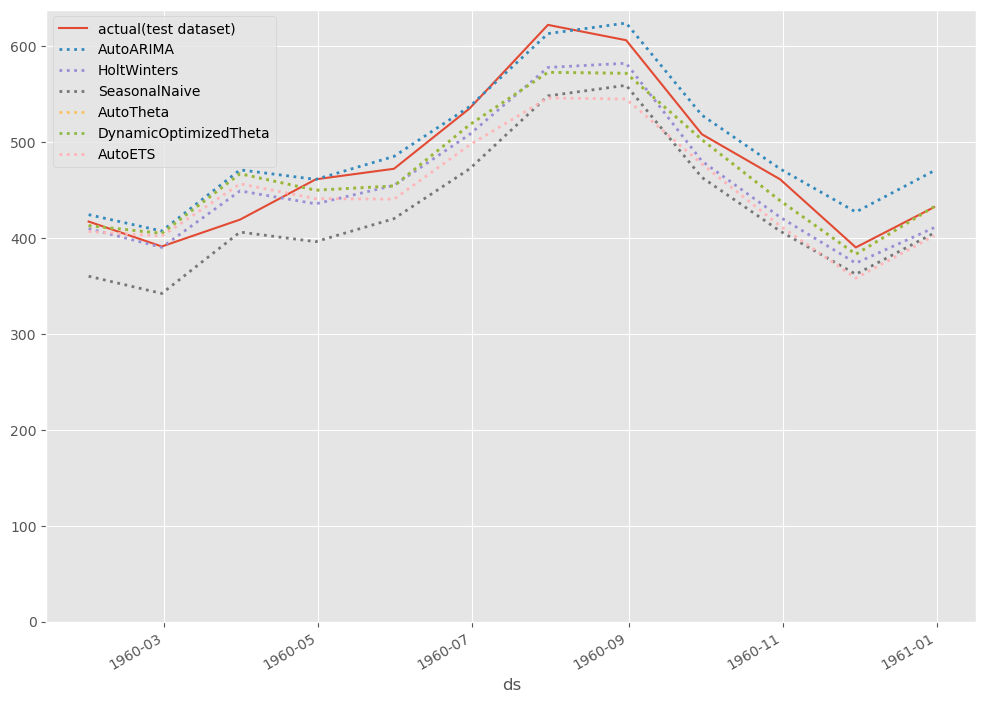
アンサンブル(平均値)
複数の予測モデルから出力された予測値の平均値を計算していきます。それが予測結果です。
以下、コードです。
# # 予測値の平均(予測結果) # y_test_pred = test_pred.iloc[:,1:7].mean(axis=1) y_train_pred = train_pred.iloc[:,2:8].mean(axis=1)
テストデータの予測結果を確認します。
以下、コードです。
# テストデータの予測結果の確認 print(pd.DataFrame(y_test_pred.values,index=test_pred.ds))
以下、実行結果です。
0 ds 1960-01-31 404.316864 1960-02-29 391.689606 1960-03-31 452.619965 1960-04-30 438.745514 1960-05-31 451.350861 1960-06-30 508.252899 1960-07-31 571.552917 1960-08-31 575.427673 1960-09-30 492.062531 1960-10-31 431.699341 1960-11-30 381.015869 1960-12-31 425.360809
テストデータ期間の予測精度を見てみます。
以下、コードです。
#
# 精度指標(テストデータ)
#
print('RMSE:')
print(np.sqrt(mean_squared_error(df_test.y, y_test_pred)))
print('MAE:')
print(mean_absolute_error(df_test.y, y_test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(df_test.y, y_test_pred))
以下、実行結果です。
RMSE: 25.241494178068326 MAE: 21.543690999348957 MAPE: 0.0432771029010986
それほど悪くはありませんが、特別良いとも言えません。
グラフ化し見てみます。
以下、コードです。
# # グラフ化 # fig, ax = plt.subplots() ax.plot(df_train.ds, df_train.y, label="actual(train dataset)") ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") ax.plot(df_train.ds, y_train_pred, linestyle="dotted", lw=2,color="m") ax.plot(df_test.ds, y_test_pred, label="Ensemble", linestyle="dotted", lw=2, color="m") ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
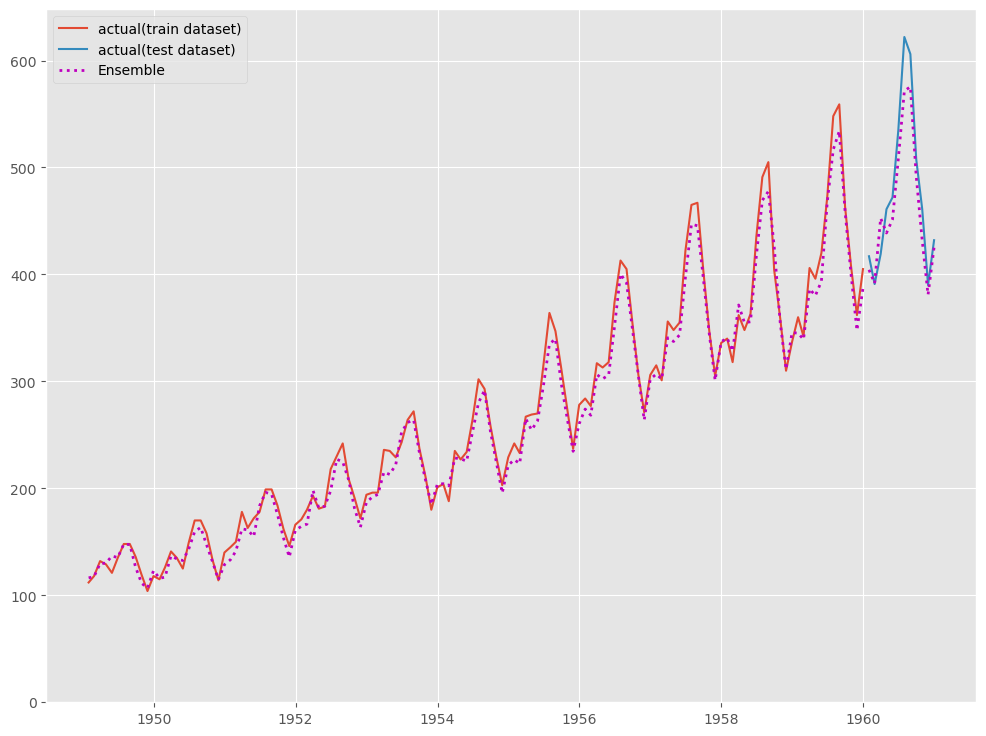
テストデータ期間のみ見てみます。
以下、コードです。
# # グラフ化 # fig, ax = plt.subplots() ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") ax.plot(df_test.ds, y_test_pred, label="Ensemble", linestyle="dotted", lw=2, color="m") ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
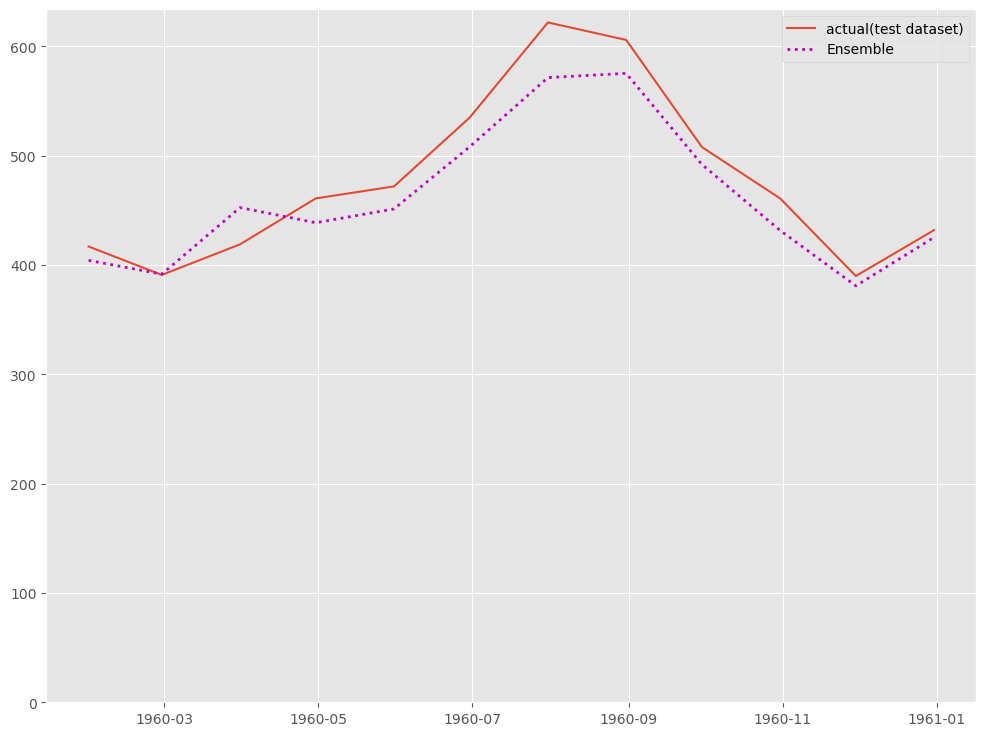
アンサンブル(重回帰)
複数の予測モデルから出力された予測値を特徴量(説明変数)とした重回帰モデルを学習します。
先ず、重回帰モデル用のデータセットを生成します。
以下、コードです。
#
# 重回帰モデル用のデータセット生成
#
dataset = pd.concat([train_pred,test_pred])
dataset = dataset.set_index('ds')
dataset['y'] = df.set_index('ds').y
dataset = dataset.dropna()
print(dataset)
以下、実行結果です。
y AutoARIMA HoltWinters SeasonalNaive AutoTheta \
ds
1950-01-31 115.0 115.426987 109.280937 112.0 121.963615
1950-02-28 126.0 121.146469 118.884819 118.0 115.647797
1950-03-31 141.0 138.800049 127.466965 132.0 144.786926
1950-04-30 135.0 137.760010 130.324829 129.0 138.185623
1950-05-31 125.0 127.719971 137.544403 121.0 138.648422
... ... ... ... ... ...
1960-08-31 606.0 623.903381 581.996765 559.0 571.371643
1960-09-30 508.0 527.903320 479.946136 463.0 502.108032
1960-10-31 461.0 471.903320 421.522797 407.0 438.527100
1960-11-30 390.0 426.903320 373.590912 362.0 382.673859
1960-12-31 432.0 469.903320 410.594971 405.0 432.116119
DynamicOptimizedTheta AutoETS
ds
1950-01-31 119.328331 117.541862
1950-02-28 112.951286 115.125816
1950-03-31 142.454269 135.798752
1950-04-30 135.978622 133.337097
1950-05-31 136.520020 133.833603
... ... ...
1960-08-31 571.621704 544.672485
1960-09-30 502.383270 477.034485
1960-10-31 438.819733 412.423096
1960-11-30 382.977936 357.949158
1960-12-31 432.517731 402.032745
[132 rows x 7 columns]
目的変数yと説明変数Xに分けます。
以下、コードです。
# 目的変数y
y = dataset.y
# 説明変数X
X = dataset.drop('y',axis=1)
目的変数yを確認してみます。
以下、コードです。
# 目的変数yの確認 print(y)
以下、実行結果です。
ds
1950-01-31 115.0
1950-02-28 126.0
1950-03-31 141.0
1950-04-30 135.0
1950-05-31 125.0
...
1960-08-31 606.0
1960-09-30 508.0
1960-10-31 461.0
1960-11-30 390.0
1960-12-31 432.0
Name: y, Length: 132, dtype: float64
説明変数Xを確認してみます。
以下、コードです。
# 説明変数Xの確認 print(X)
以下、実行結果です。
AutoARIMA HoltWinters SeasonalNaive AutoTheta \
ds
1950-01-31 115.426987 109.280937 112.0 121.963615
1950-02-28 121.146469 118.884819 118.0 115.647797
1950-03-31 138.800049 127.466965 132.0 144.786926
1950-04-30 137.760010 130.324829 129.0 138.185623
1950-05-31 127.719971 137.544403 121.0 138.648422
... ... ... ... ...
1960-08-31 623.903381 581.996765 559.0 571.371643
1960-09-30 527.903320 479.946136 463.0 502.108032
1960-10-31 471.903320 421.522797 407.0 438.527100
1960-11-30 426.903320 373.590912 362.0 382.673859
1960-12-31 469.903320 410.594971 405.0 432.116119
DynamicOptimizedTheta AutoETS
ds
1950-01-31 119.328331 117.541862
1950-02-28 112.951286 115.125816
1950-03-31 142.454269 135.798752
1950-04-30 135.978622 133.337097
1950-05-31 136.520020 133.833603
... ... ...
1960-08-31 571.621704 544.672485
1960-09-30 502.383270 477.034485
1960-10-31 438.819733 412.423096
1960-11-30 382.977936 357.949158
1960-12-31 432.517731 402.032745
[132 rows x 6 columns]
学習データとテストデータ(直近12カ月間)へ分割します。
以下、コードです。
# # 学習データとテストデータ(直近12ヶ月間)へ分割 # # 学習データ y_train = y[:-12] X_train = X[:-12] # テストデータ y_test = y[-12:] X_test = X[-12:]
学習データを使い、重回帰モデルを学習します。
以下、コードです。
# # 学習 # model = LinearRegression() model.fit(X_train, y_train)
学習した重回帰モデルを使い、予測します。
以下、コードです。
# # 予測 # # テストデータ期間 y_test_pred = model.predict(X_test) # 学習データ期間 y_train_pred = model.predict(X_train)
テストデータの予測結果を確認します。
以下、コードです。
# テストデータの予測結果の確認 print(pd.DataFrame(y_test_pred,index=X_test.index))
以下、実行結果です。
0 ds 1960-01-31 414.696777 1960-02-29 399.045380 1960-03-31 466.506775 1960-04-30 449.620483 1960-05-31 464.420593 1960-06-30 529.268372 1960-07-31 596.430420 1960-08-31 598.346741 1960-09-30 510.280518 1960-10-31 447.608917 1960-11-30 392.959106 1960-12-31 441.324249
テストデータ期間の予測精度を見てみます。
以下、コードです。
#
# 精度指標(テストデータ)
#
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, y_test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, y_test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, y_test_pred))
以下、実行結果です。
RMSE: 17.173901214177544 MAE: 11.976977030436197 MAPE: 0.025615260706653386
かなり予測精度が良くなりました。
グラフ化し見てみます。
以下、コードです。
# # グラフ化 # fig, ax = plt.subplots() ax.plot(y_train, label="actual(train dataset)") ax.plot(y_test, label="actual(test dataset)") ax.plot(y_train.index, y_train_pred, linestyle="dotted", lw=2,color="m") ax.plot(y_test.index, y_test_pred, label="Ensemble", linestyle="dotted", lw=2, color="m") ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
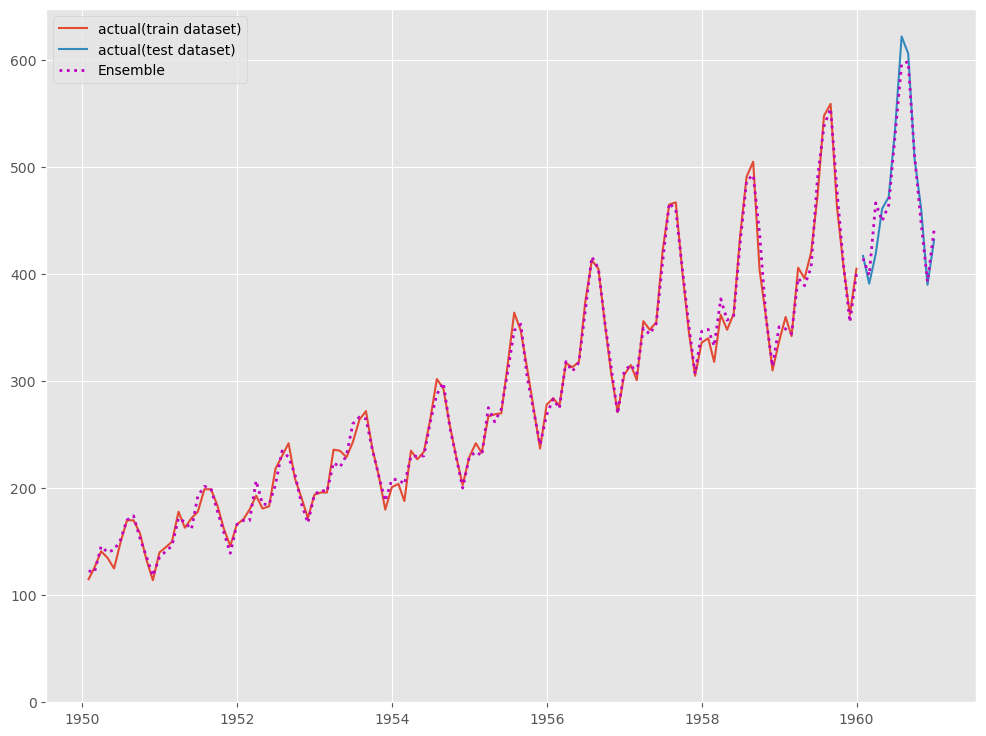
テストデータ期間のみ見てみます。
以下、コードです。
# # グラフ化 # fig, ax = plt.subplots() ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") ax.plot(df_test.ds, y_test_pred, label="Ensemble", linestyle="dotted", lw=2, color="m") ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
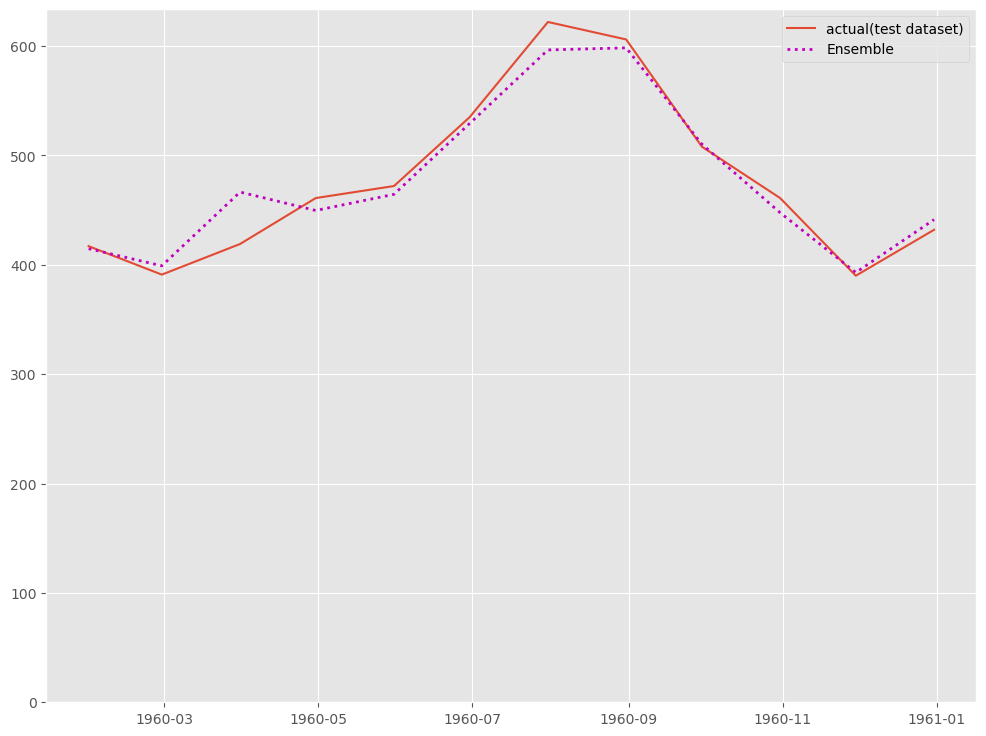
WineSales(ワイン販売数)
データの読み込み
データセットを読み込みます。
以下、コードです。
#
# データの読み込み
#
dataset = sm.datasets.get_rdataset('wineind', 'forecast')
print(dataset.data) #確認
以下、実行結果です。
time value 0 1980.000000 15136 1 1980.083333 16733 2 1980.166667 20016 3 1980.250000 17708 4 1980.333333 18019 .. ... ... 171 1994.250000 26323 172 1994.333333 23779 173 1994.416667 27549 174 1994.500000 29660 175 1994.583333 23356 [176 rows x 2 columns]
StatsForecastで扱える形式に整えます。
以下、コードです。
#
# StatsForecastで扱える形式に整える
#
df = pd.DataFrame(
{
'unique_id':1,
'ds': pd.date_range(start="1980/1/1",freq="m",periods=176),
'y': dataset.data.value,
},
)
print(df) #確認
以下、実行結果です。
unique_id ds y 0 1 1980-01-31 15136 1 1 1980-02-29 16733 2 1 1980-03-31 20016 3 1 1980-04-30 17708 4 1 1980-05-31 18019 .. ... ... ... 171 1 1994-04-30 26323 172 1 1994-05-31 23779 173 1 1994-06-30 27549 174 1 1994-07-31 29660 175 1 1994-08-31 23356 [176 rows x 3 columns]
学習データとテストデータ(直近12カ月間)へ分割します。
以下、コードです。
# # 学習データとテストデータ(直近12カ月間)へ分割 # # 学習データ df_train = df[:-12] # テストデータ df_test = df[-12:]
学習データを確認してみます。
以下、コードです。
# 学習データの確認 print(df_train)
以下、実行結果です。
unique_id ds y 0 1 1980-01-31 15136 1 1 1980-02-29 16733 2 1 1980-03-31 20016 3 1 1980-04-30 17708 4 1 1980-05-31 18019 .. ... ... ... 159 1 1993-04-30 26805 160 1 1993-05-31 25236 161 1 1993-06-30 24735 162 1 1993-07-31 29356 163 1 1993-08-31 31234 [164 rows x 3 columns]
テストデータを確認してみます。
以下、コードです。
# テストデータの確認 print(df_test)
以下、実行結果です。
unique_id ds y 164 1 1993-09-30 22724 165 1 1993-10-31 28496 166 1 1993-11-30 32857 167 1 1993-12-31 37198 168 1 1994-01-31 13652 169 1 1994-02-28 22784 170 1 1994-03-31 23565 171 1 1994-04-30 26323 172 1 1994-05-31 23779 173 1 1994-06-30 27549 174 1 1994-07-31 29660 175 1 1994-08-31 23356
グラフ化し確認してみます。
以下、コードです。
# グラフ化 fig, ax = plt.subplots() ax.plot(df_train.ds, df_train.y, label="actual(train dataset)") ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") ax.axes.xaxis.set_visible(False) ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。

複数モデルの構築
先ず、複数の予測モデルを構築していきます。
そのために、構築する予測モデルのアルゴリズムのリスト(モデルリスト)を作成します。
以下、コードです。
#
# モデルリストの作成
#
PERIOD = 12
models = [
AutoARIMA(season_length=PERIOD),
HoltWinters(season_length=PERIOD),
SeasonalNaive(season_length=PERIOD),
AutoTheta(season_length=PERIOD),
DOT(season_length=PERIOD),
AutoETS(season_length=PERIOD),
]
学習します。
以下、コードです。
#
# 時系列予測モデルの学習
#
# インスタンス生成
sf = StatsForecast(
models = models,
freq = 'M',
n_jobs=-1,
)
# 学習(学習データ)
sf.fit(df_train)
予測を実施します。
以下、コードです。
# # 予測の実施 # # テストデータ期間 test_pred = sf.forecast(len(df_test),fitted=True) # 学習データ期間 train_pred = sf.forecast_fitted_values()
テストデータ期間の予測結果を確認します。
以下、コードです。
# テストデータの予測結果の確認 print(test_pred)
以下、実行結果です。
ds AutoARIMA HoltWinters SeasonalNaive AutoTheta \
unique_id
1 1993-09-30 25720.443359 25806.755859 25156.0 25328.417969
1 1993-10-31 26873.044922 27066.654297 25650.0 26693.591797
1 1993-11-30 32086.277344 32444.990234 30923.0 31901.193359
1 1993-12-31 37347.332031 37168.160156 37240.0 36773.554688
1 1994-01-31 18447.267578 19518.896484 17466.0 18190.744141
1 1994-02-28 21157.449219 22328.550781 19463.0 21149.164062
1 1994-03-31 24839.212891 25611.074219 24352.0 24453.267578
1 1994-04-30 26366.576172 26311.923828 26805.0 25261.683594
1 1994-05-31 25126.273438 25911.855469 25236.0 24701.000000
1 1994-06-30 24880.539062 25576.244141 24735.0 24293.765625
1 1994-07-31 30162.029297 30888.460938 29356.0 29634.562500
1 1994-08-31 30170.083984 30876.755859 31234.0 29544.162109
DynamicOptimizedTheta AutoETS
unique_id
1 25353.738281 25200.136719
1 26719.343750 26651.212891
1 31930.863281 31660.291016
1 36806.496094 36425.386719
1 18206.416016 18212.419922
1 21166.671875 21052.523438
1 24472.685547 24393.921875
1 25280.900391 25375.265625
1 24718.972656 24501.708984
1 24310.640625 24180.208984
1 29654.179688 29449.763672
1 29562.757812 29938.888672
学習データ期間の予測結果を確認します。
以下、コードです。
# 学習データの予測結果の確認 print(train_pred)
以下、実行結果です。
ds y AutoARIMA HoltWinters SeasonalNaive \
unique_id
1 1980-01-31 15136.0 15127.260742 12973.968750 NaN
1 1980-02-29 16733.0 16727.855469 15914.354492 NaN
1 1980-03-31 20016.0 20009.857422 19257.726562 NaN
1 1980-04-30 17708.0 17705.457031 20022.988281 NaN
1 1980-05-31 18019.0 18016.689453 19488.566406 NaN
... ... ... ... ... ...
1 1993-04-30 26805.0 24846.925781 24965.792969 23757.0
1 1993-05-31 25236.0 24363.072266 24650.830078 25013.0
1 1993-06-30 24735.0 23898.470703 24332.656250 24019.0
1 1993-07-31 29356.0 29871.386719 29655.939453 30345.0
1 1993-08-31 31234.0 27069.568359 29610.015625 24488.0
AutoTheta DynamicOptimizedTheta AutoETS
unique_id
1 15136.000000 15136.000000 14614.176758
1 17591.060547 16819.916016 16969.451172
1 19290.421875 18583.732422 19627.498047
1 20545.875000 19840.787109 20476.300781
1 18619.939453 18108.027344 19422.121094
... ... ... ...
1 24550.865234 24536.003906 24657.693359
1 24228.806641 24232.750000 24076.099609
1 23929.789062 23940.388672 23907.376953
1 29290.353516 29308.763672 29248.238281
1 29208.222656 29224.103516 29745.482422
[164 rows x 8 columns]
テストデータ期間の予測精度を見てみます。
以下、コードです。
#
# 精度指標(テストデータ)
#
for i in range(1,7) :
print(test_pred.columns[i])
print('\t'+'RMSE:'+'\t',
np.sqrt(mean_squared_error(df_test.y, test_pred.iloc[:,i])))
print('\t'+'MAE:'+'\t',
mean_absolute_error(df_test.y, test_pred.iloc[:,i]))
print('\t'+'MAPE:'+'\t',
mean_absolute_percentage_error(df_test.y, test_pred.iloc[:,i]))
以下、実行結果です。
AutoARIMA RMSE: 2815.3500207871384 MAE: 2050.9090169270835 MAPE: 0.09640424878808153 HoltWinters RMSE: 3123.0757960277006 MAE: 2182.3562825520835 MAPE: 0.1050727559379744 SeasonalNaive RMSE: 3114.2218798066824 MAE: 2342.5833333333335 MAPE: 0.10455805468090233 AutoTheta RMSE: 2677.908377817492 MAE: 2025.0896809895833 MAPE: 0.0936110047613043 DynamicOptimizedTheta RMSE: 2680.885301527278 MAE: 2019.7062174479167 MAPE: 0.09354213357886888 AutoETS RMSE: 2771.792032215696 MAE: 2103.61865234375 MAPE: 0.09614448379415981
グラフ化し見てみます。
以下、コードです。
# # グラフ化 # # グラフ用データ(学習データにテストデータ期間の予測結果を結合) pred = pd.concat([df_train,test_pred]).drop(['y','unique_id','ds'], axis=1) pred.index = df.ds # グラフ描写 fig, ax = plt.subplots() ax.plot(df_train.ds, df_train.y, label="actual(train dataset)") ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") pred.plot(ax=ax, linestyle="dotted", lw=2) ax.axes.xaxis.set_visible(False) ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
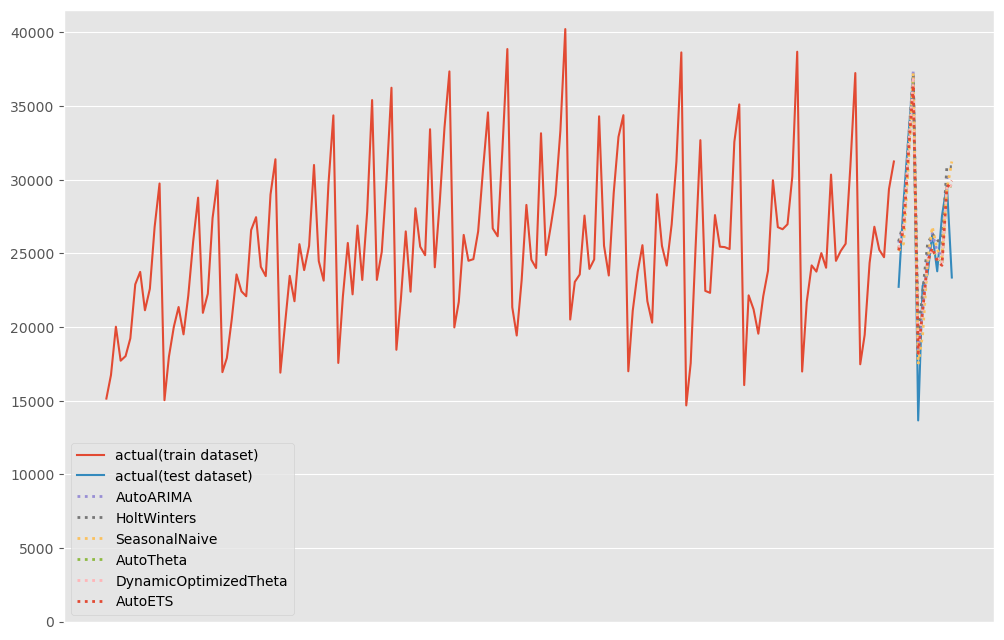
テストデータ期間のみ見てみます。
以下、コードです。
# # グラフ化 # # グラフ用データ(テストデータ期間のみ抽出) pred_test = pred[-12:] # グラフ描写 fig, ax = plt.subplots() ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") pred_test.plot(ax=ax, linestyle="dotted", lw=2) ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
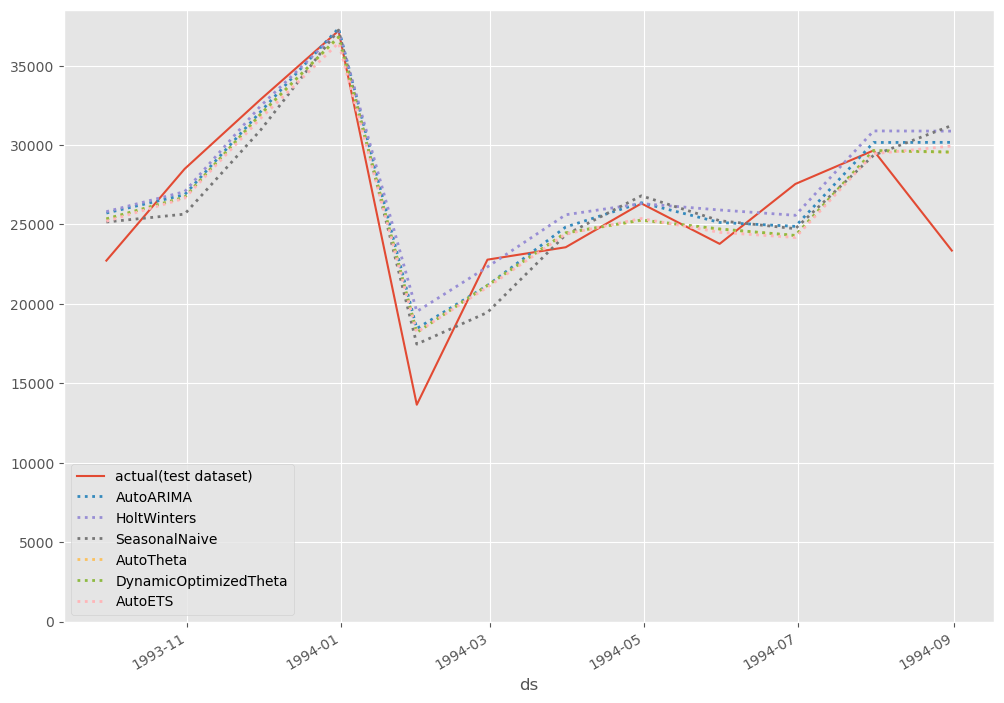
アンサンブル(平均値)
複数の予測モデルから出力された予測値の平均値を計算していきます。それが予測結果です。
以下、コードです。
# # 予測値の平均を計算 # y_test_pred = test_pred.iloc[:,1:7].mean(axis=1) y_train_pred = train_pred.iloc[:,2:8].mean(axis=1)
テストデータの予測結果を確認します。
以下、コードです。
# テストデータの予測結果の確認 print(pd.DataFrame(y_test_pred.values,index=test_pred.ds))
以下、実行結果です。
0 ds 1993-09-30 25427.580078 1993-10-31 26608.976562 1993-11-30 31824.437500 1993-12-31 36960.156250 1994-01-31 18340.291016 1994-02-28 21052.892578 1994-03-31 24687.025391 1994-04-30 25900.224609 1994-05-31 25032.632812 1994-06-30 24662.732422 1994-07-31 29857.500000 1994-08-31 30221.109375
テストデータ期間の予測精度を見てみます。
以下、コードです。
#
# 精度指標(テストデータ)
#
print('RMSE:')
print(np.sqrt(mean_squared_error(df_test.y, y_test_pred)))
print('MAE:')
print(mean_absolute_error(df_test.y, y_test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(df_test.y, y_test_pred))
以下、実行結果です。
RMSE: 2820.7314648500337 MAE: 2085.6432291666665 MAPE: 0.09701371570832255
それほど悪くはありませんが、特別良いとも言えません。
グラフ化し見てみます。
以下、コードです。
# # グラフ化 # fig, ax = plt.subplots() ax.plot(df_train.ds, df_train.y, label="actual(train dataset)") ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") ax.plot(df_train.ds, y_train_pred, linestyle="dotted", lw=2,color="m") ax.plot(df_test.ds, y_test_pred, label="Ensemble", linestyle="dotted", lw=2, color="m") ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
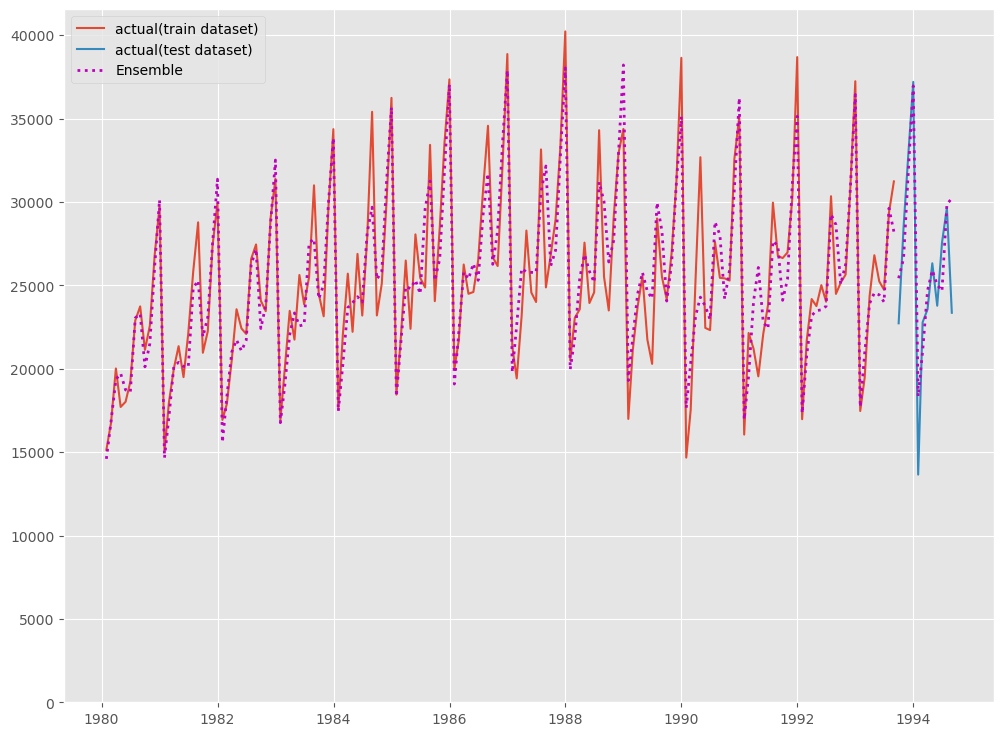
テストデータ期間のみ見てみます。
以下、コードです。
# # グラフ化 # fig, ax = plt.subplots() ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") ax.plot(df_test.ds, y_test_pred, label="Ensemble", linestyle="dotted", lw=2, color="m") ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
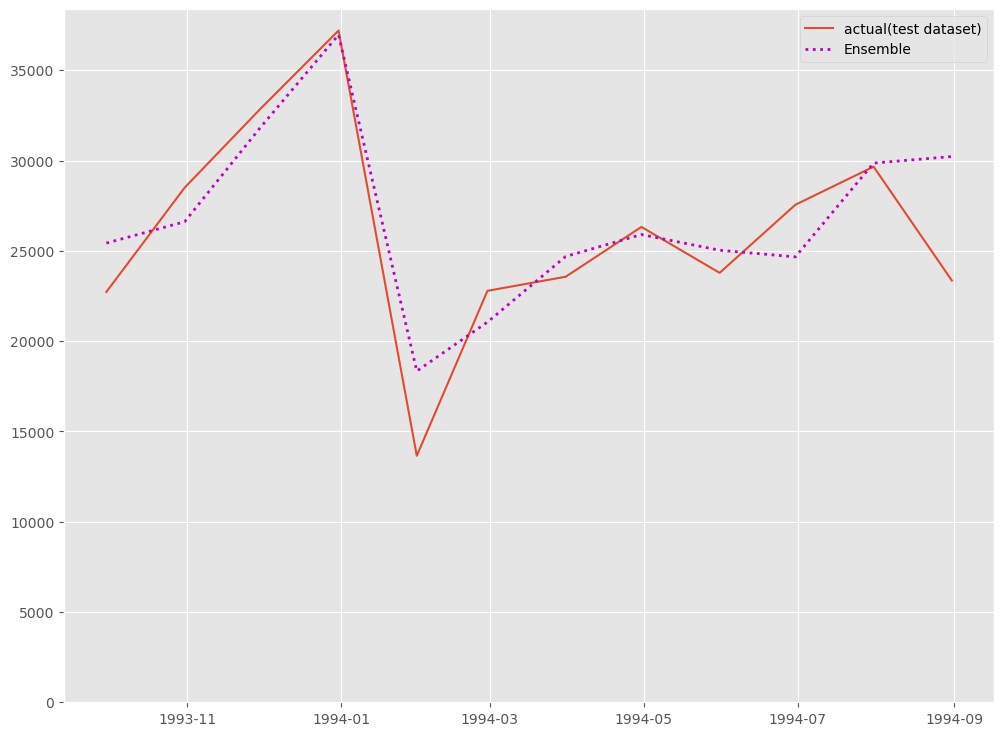
アンサンブル(重回帰)
複数の予測モデルから出力された予測値を特徴量(説明変数)とした重回帰モデルを学習します。
先ず、重回帰モデル用のデータセットを生成します。
以下、コードです。
#
# 重回帰モデル用のデータセット生成
#
dataset = pd.concat([train_pred,test_pred])
dataset = dataset.set_index('ds')
dataset['y'] = df.set_index('ds').y
dataset = dataset.dropna()
print(dataset)
以下、実行結果です。
y AutoARIMA HoltWinters SeasonalNaive AutoTheta \
ds
1981-09-30 20960 23087.634766 21782.914062 21133.0 22079.109375
1981-10-31 22254 24215.552734 23026.416016 22591.0 23135.904297
1981-11-30 27392 28287.804688 28387.013672 26786.0 27539.898438
1981-12-31 29945 31063.466797 33065.714844 29740.0 31769.185547
1982-01-31 16933 16742.128906 15225.994141 15028.0 15608.688477
... ... ... ... ... ...
1994-04-30 26323 26366.576172 26311.923828 26805.0 25261.683594
1994-05-31 23779 25126.273438 25911.855469 25236.0 24701.000000
1994-06-30 27549 24880.539062 25576.244141 24735.0 24293.765625
1994-07-31 29660 30162.029297 30888.460938 29356.0 29634.562500
1994-08-31 23356 30170.085938 30876.755859 31234.0 29544.162109
DynamicOptimizedTheta AutoETS
ds
1981-09-30 21948.890625 21448.113281
1981-10-31 23008.423828 22619.792969
1981-11-30 27398.462891 26811.078125
1981-12-31 31619.164062 30927.970703
1982-01-31 15538.637695 15405.576172
... ... ...
1994-04-30 25280.900391 25375.265625
1994-05-31 24718.972656 24501.708984
1994-06-30 24310.640625 24180.208984
1994-07-31 29654.179688 29449.763672
1994-08-31 29562.757812 29938.888672
[156 rows x 7 columns]
目的変数yと説明変数Xに分けます。
以下、コードです。
# 目的変数y
y = dataset.y
# 説明変数X
X = dataset.drop('y',axis=1)
目的変数yを確認してみます。
以下、コードです。
# 目的変数yの確認 print(y)
以下、実行結果です。
ds
1981-09-30 20960
1981-10-31 22254
1981-11-30 27392
1981-12-31 29945
1982-01-31 16933
...
1994-04-30 26323
1994-05-31 23779
1994-06-30 27549
1994-07-31 29660
1994-08-31 23356
Name: y, Length: 156, dtype: int64
説明変数Xを確認してみます。
以下、コードです。
# 説明変数Xの確認 print(X)
以下、実行結果です。
AutoARIMA HoltWinters SeasonalNaive AutoTheta \
ds
1981-09-30 23087.634766 21782.914062 21133.0 22079.109375
1981-10-31 24215.552734 23026.416016 22591.0 23135.904297
1981-11-30 28287.804688 28387.013672 26786.0 27539.898438
1981-12-31 31063.466797 33065.714844 29740.0 31769.185547
1982-01-31 16742.128906 15225.994141 15028.0 15608.688477
... ... ... ... ...
1994-04-30 26366.576172 26311.923828 26805.0 25261.683594
1994-05-31 25126.273438 25911.855469 25236.0 24701.000000
1994-06-30 24880.539062 25576.244141 24735.0 24293.765625
1994-07-31 30162.029297 30888.460938 29356.0 29634.562500
1994-08-31 30170.085938 30876.755859 31234.0 29544.162109
DynamicOptimizedTheta AutoETS
ds
1981-09-30 21948.890625 21448.113281
1981-10-31 23008.423828 22619.792969
1981-11-30 27398.462891 26811.078125
1981-12-31 31619.164062 30927.970703
1982-01-31 15538.637695 15405.576172
... ... ...
1994-04-30 25280.900391 25375.265625
1994-05-31 24718.972656 24501.708984
1994-06-30 24310.640625 24180.208984
1994-07-31 29654.179688 29449.763672
1994-08-31 29562.757812 29938.888672
[156 rows x 6 columns]
学習データとテストデータ(直近12カ月間)へ分割します。
以下、コードです。
# # 学習データとテストデータ(直近12ヶ月間)へ分割 # # 学習データ y_train = y[:-12] X_train = X[:-12] # テストデータ y_test = y[-12:] X_test = X[-12:]
学習データを使い、重回帰モデルを学習します。
以下、コードです。
# # 学習 # model = LinearRegression() model.fit(X_train, y_train)
学習した重回帰モデルを使い、予測します。
以下、コードです。
# # 予測 # # テストデータ期間 y_test_pred = model.predict(X_test) # 学習データ期間 y_train_pred = model.predict(X_train)
テストデータの予測結果を確認します。
以下、コードです。
# テストデータの予測結果の確認 print(pd.DataFrame(y_test_pred,index=X_test.index))
以下、実行結果です。
0 ds 1993-09-30 25662.535156 1993-10-31 26629.332031 1993-11-30 31795.601562 1993-12-31 36871.882812 1994-01-31 19152.087891 1994-02-28 21589.574219 1994-03-31 25312.744141 1994-04-30 26453.144531 1994-05-31 25838.560547 1994-06-30 25389.544922 1994-07-31 30244.296875 1994-08-31 31085.597656
テストデータ期間の予測精度を見てみます。
以下、コードです。
#
# 精度指標(テストデータ)
#
print('RMSE:')
print(np.sqrt(mean_squared_error(y_test, y_test_pred)))
print('MAE:')
print(mean_absolute_error(y_test, y_test_pred))
print('MAPE:')
print(mean_absolute_percentage_error(y_test, y_test_pred))
以下、実行結果です。
RMSE: 3123.761658790124 MAE: 2274.8359375 MAPE: 0.10716243803860785
悪くはないですが、それほど良い感じでもありません。
グラフ化し見てみます。
以下、コードです。
# # グラフ化 # fig, ax = plt.subplots() ax.plot(y_train, label="actual(train dataset)") ax.plot(y_test, label="actual(test dataset)") ax.plot(y_train.index, y_train_pred, linestyle="dotted", lw=2,color="m") ax.plot(y_test.index, y_test_pred, label="Ensemble", linestyle="dotted", lw=2, color="m") ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
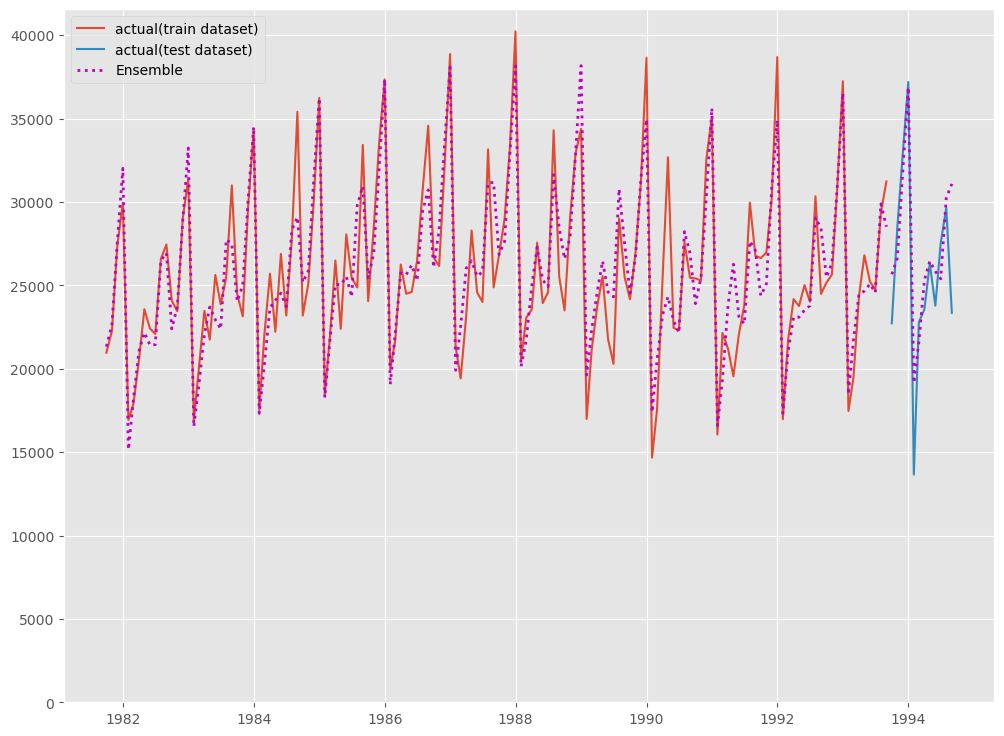
テストデータ期間のみ見てみます。
以下、コードです。
# # グラフ化 # fig, ax = plt.subplots() ax.plot(df_test.ds, df_test.y, label="actual(test dataset)") ax.plot(df_test.ds, y_test_pred, label="Ensemble", linestyle="dotted", lw=2, color="m") ax.set_ylim(ymin=0) ax.legend() plt.show()
以下、実行結果です。
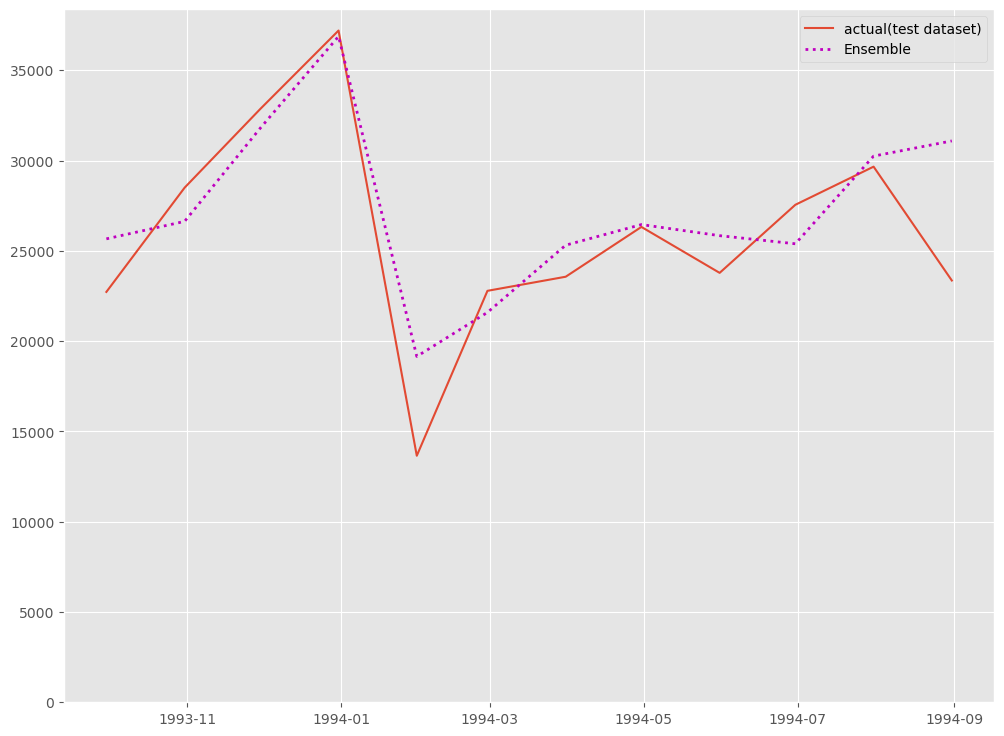
まとめ
今回は、「StatsForecast で時系列アンサンブル学習による予測」というお話しをしました。
StatsForecastは簡単に多くの種類の統計学系の時系列予測モデルをさくっと作れ、それを使いアンサンブルな予測モデルもさくっと作れます。
興味のある方は、試してみてください。

![[Python] StatsForecast で時系列アンサンブル学習による予測](https://www.salesanalytics.co.jp/wp-content/uploads/2023/04/546ddae298dce7391135667626d88671.png)