時系列モデルを構築するとき、季節成分をモデルに組み込むことが多いです。
季節成分をモデルに組み込むには、その周期期間を知らなくてはなりません。

多くの場合、ドメイン知識(時系列モデルを活用する現場の知識など)をもとに、1年周期や7日間周期、24時間周期などとすることが多いです。
このように分かりやすいものもありますが、不明な場合もあります。
そもそも、本当にそうなのか、そうであっても組み込むほどのものなのか、という疑問もあります。

そこで登場するのが、季節成分の周期期間の検出技術です。
周期の期間とその強さの検出をするデータサイエンス技術で、例えば次のようなものが古くからあります。
- 自己相関分析
- スペクトル分析
- 周期性テスト
今回は、自己相関分析による周期の長さの見つけ方を説明します。
Contents
自己相関とは?
自己相関(Autocorrelation)を考えるとき、「ラグ」という概念抜きにしては語れません。
ラグとは、観測値間の時間的なずれまたは遅延を指します。ラグ1は前の時点の観測値を指し、ラグ2はラグ1の前の時点(要は、前の前の時点)の観測値を指す、といった具体的です。
ラグは時系列データ内での時間的な関連性を表現するための重要な概念です。
時間的な関連性を表現する指標の1つに自己相関(Autocorrelation)があります。
自己相関とは、時系列データ内の一連の観測値が、それ自体のラグとどの程度相関しているかを示した相関係数で、ある時点のデータが他の時点のデータとどれだけ関連しているかを表します。
例えば、毎月の気温のデータを考えると……
- ラグ1の自己相関:前の月(1か月前)との相関
- ラグ12の自己相関:前の年と同じ月(12か月前)との相関
自己相関の双子の兄弟がいます。偏自己相関(Partial Autocorrelation)です。
偏自己相関は、特定のラグ(例えばラグk)の影響が、それよりも小さいラグ(例えばラグ1からラグk-1)の影響を除いた後でどれだけ残るかを示したものです。
自己相関分析で周期期間をどのように特定するの?
自己相関分析による、周期期間の特定は非常にシンプルです。
単に、自動相関の高いラグを見つければいいからです。その自己相関の大きさが、季節成分の強さです。
そのために、自己相関(Autocorrelation)と偏自己相関(Partial Autocorrelation)を求めグラフ化します。
次の2つのグラフを作ります。
ACF(Autocorrelation、自己相関)プロット
各ラグ(遅延)における自己相関を示します。y軸は自己相関の値(-1から1)を、x軸はラグの値(通常、時間の単位)を示します。各棒の高さはそのラグにおける自己相関の大きさを示し、棒が信頼区間(背景が薄い赤の領域)を超えている場合、そのラグの自己相関は統計的に有意であると解釈されます。
PACF(Partial Autocorrelation、偏自己相関)プロット
他のラグが制御されたときの各ラグ間の相関を示します。これは、時系列の特定のラグが他のラグを通じてではなく、直接的に前の観測値に影響を与える程度を測定します。
以下のようなACFプロット(上のプロット)とPACFプロット(下のプロット)が得られたとします。
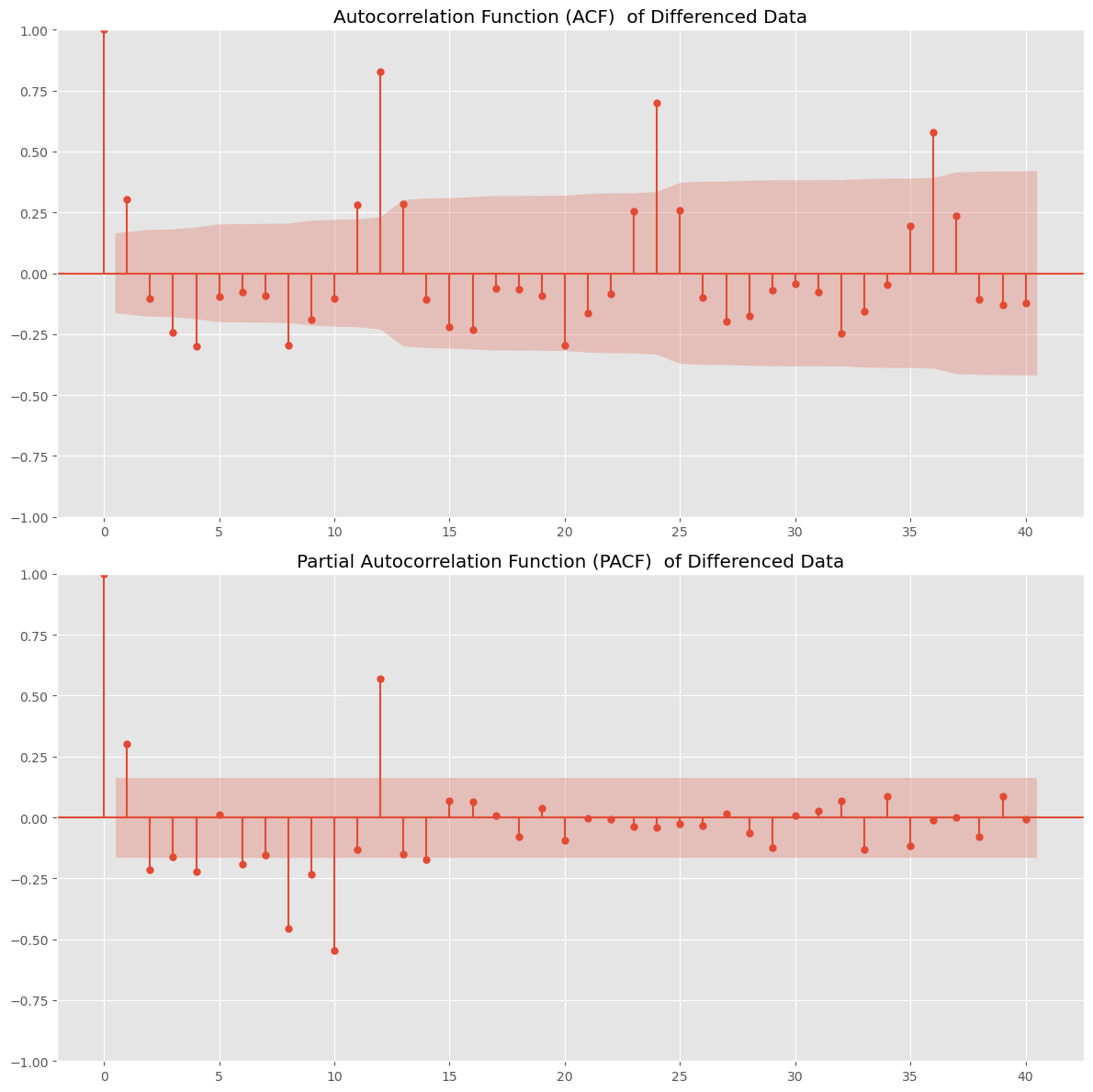
ACFプロット(上のプロット)もPACFプロット(下のプロット)も、一番左のラグ0の相関係数は1と一番大きくなります。
自分自身との相関なので相関係数が1となるのは、当然と言えば当然です。ラグ0以外のラグの相関係数を見ていきます。
では、ACFプロット(上のプロット)を見てみます。
ラグ12とラグ24の自己相関が高いことが分かります。
季節性の周期は12周期と24周期の2つがあるかもしれません。
本当でしょうか?

そこで、PACFプロット(下のプロット)を見てみます。
偏自己相関を見たら、ラグ12の偏自己相関が高く、ラグ24の偏自己相関が小さいようです。
このようなとき、季節性の周期は12周期である可能性が高いですが、24周期はない可能性が高いです。
24周期があるように見えたのは、単に12周期の影響によるもの(一昨年と昨年が相関、昨年と今年が相関)と解釈できます。
トレンド非定常を除去すると見つけやすくなる
自己相関分析で時系列データの季節成分の周期期間を検討するとき、トレンド非定常性を除去してあると見つけやすくなります。
トレンド非定常性とは何? そもそも非定常って何? と思われた方は以下の記事を参考にしてください。
定常性とは、時系列データに求められる前提となる条件というか理想の性質で、定常な時系列データに近づけようと色々な処理を施すことが多いです。
定常性でない時系列データは非定常と呼ばれ、主に3つの非定常性があります。
- トレンド非定常性
- 季節性非定常性
- 分散非定常性
厳密ではありませんが、よくあるアプローチは「トレンド非定常性に対処→季節性非定常性に対処→分散非定常性に対処」というものです。
このアプローチで時系列モデルを構築するとき、トレンド成分を組み込むことでトレンド非定常性に対処し、季節成分を茎混むことで季節性非定常性に対処し、という感じで定常な時系列データに近づけていきます。
要するに、時系列データの季節成分の周期期間を検討するとき、トレンド非定常性を除去した時系列データで対し自己相関分析を実施し、季節成分の周期期間を探すというのが王道です(たぶん)。
繰り返しになりますが、自己相関分析で時系列データの季節成分の周期期間を検討するとき、トレンド非定常性を除去してあると見つけやすくなる、という側面もあります。
サンプルデータ
時系列データの分析例でよく登場する「航空旅客データ」(AirPassengers)を使います。
航空旅客データは、国際航空旅客の月次データを指します。具体的には、1949年から1960年までの12年間の国際航空旅客数(単位: 1000人)を含む時系列データです。各データポイントは、その月の旅客数を示しています。
このデータセットは周期性(季節性)とトレンド(一般的に増加しています)の両方を含んでいます。特に、旅行の高シーズンやオフシーズンに対応する明確な季節的なパターンが見られます。このような特性から、航空旅客データは時系列分析の手法を学習したり、試したりするためのクラシックなデータセットとして広く使われています。
Pythonのstatsmodelsライブラリでは、このデータセットを’AirPassengers’という名前で取得することができます。このデータセットを使って、時系列分析の各種手法(例えば、移動平均、指数平滑、ARIMA、季節調整など)を試すことができます。
周期期間の検出例
自己相関分析で時系列データの季節成分の周期期間を検討していきます。
次の2つのパターンで実施していきます。
- トレンド非定常性を除去しない場合
- トレンド非定常性を除去した場合
「トレンド非定常性を除去しない場合」とは、トレンド非定常性の除去をせず、元の時系列データのまま自己相関分析を実施する場合です。
「トレンド非定常性を除去した場合」とは、トレンド非定常性の除去をした時系列データに対し、自己相関分析を実施する場合です。
準備(モジュールとデータの読み込み)
先ず、必要なモジュールを読み込みます。
以下、コードです。
import pandas as pd
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = [12, 9]
import pandas as pd: pandasというライブラリをインポートします。pandasはデータ分析と操作のための強力なツールで、特に表形式のデータや時系列データの操作に適しています。pdという別名をつけることで、後続のコードで短い名前でライブラリを参照できます。import statsmodels.api as sm: statsmodelsというライブラリのAPIをインポートします。statsmodelsは、統計モデルの推定、統計テスト、データ探索などを行うためのライブラリです。smという別名をつけることで、後続のコードで短い名前でライブラリを参照できます。from statsmodels.graphics.tsaplots import plot_acf, plot_pacf: statsmodelsライブラリの中のtsaplotsモジュールからplot_acfとplot_pacfという関数をインポートします。これらの関数は、自己相関関数(ACF)と偏自己相関関数(PACF)のプロットを作成するためのものです。import matplotlib.pyplot as plt: matplotlibというライブラリのpyplotモジュールをインポートします。matplotlibは、Pythonでグラフを描画するためのライブラリで、pyplotはその中でも特にMATLAB風のインターフェイスを提供するモジュールです。pltという別名をつけることで、後続のコードで短い名前でライブラリを参照できます。plt.style.use('ggplot'): matplotlibのスタイルを’ggplot’に設定します。’ggplot’は、Rの可視化パッケージggplot2に触発されたスタイルで、グラフにはデフォルトでグリッドが表示され、色やラインスタイルなども特徴的です。plt.rcParams['figure.figsize'] = [12, 9]: matplotlibのfigureのデフォルトのサイズを設定します。この行は、すべての新規に作成されるfigureが幅12インチ、高さ9インチになるように設定します。
次に、データセットを読み込みます。
以下、コードです。
# StatsmodelsからAirPassengersデータセットをロード
dataset = sm.datasets.get_rdataset('AirPassengers')
# 時系列データを抽出
data = dataset.data['value']
# 時系列データをプロット
plt.figure(figsize=(12, 6))
plt.plot(data)
plt.title('Air Passengers Over Time')
plt.grid(True)
plt.show()
dataset = sm.datasets.get_rdataset('AirPassengers'): StatsmodelsライブラリからAirPassengersというデータセットをロードします。このデータセットは、1949年から1960年までの月別の国際航空旅客数を含んでいます。データセットはdatasetという変数に保存されます。data = dataset.data['value']: データセットから時系列データを抽出します。具体的には、データセットの’data’属性から’value’列を抽出しています。この列は航空旅客数を表しています。抽出したデータはdataという変数に保存されます。plt.figure(figsize=(12, 6)): 新しいfigureを作成し、そのサイズを幅12インチ、高さ6インチに設定します。plt.plot(data):dataのプロットを作成します。x軸はデータのインデックス(この場合は年月)を、y軸は旅客数を表しています。plt.title('Air Passengers Over Time'): プロットのタイトルを設定します。タイトルは’Air Passengers Over Time’となります。plt.grid(True): グリッド線をプロットに表示します。plt.show(): プロットを表示します。これまでのプロット設定を適用し、結果のグラフを表示します。
以下、実行結果です。
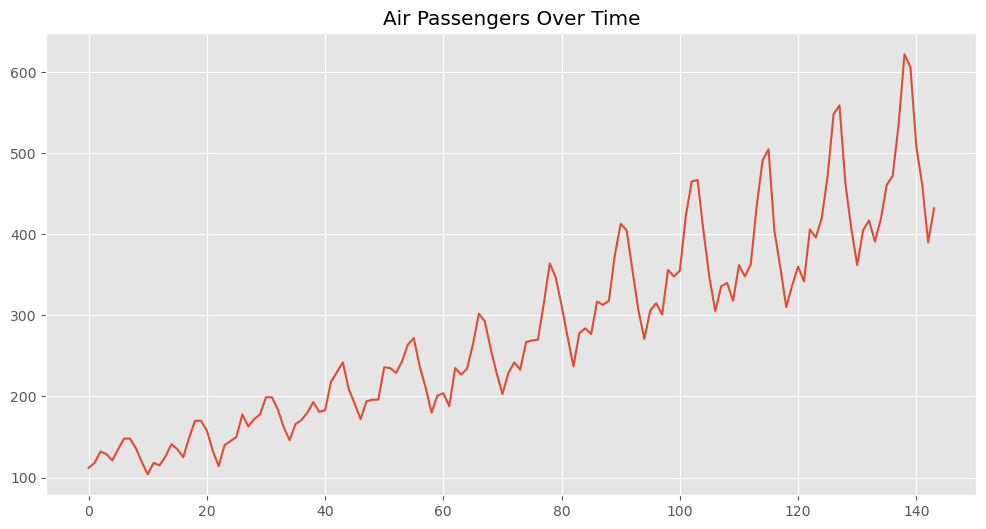
トレンド非定常性を除去しない場合
では、トレンド非定常性の除去をせず、元の時系列データのまま自己相関分析を実施していきます。
いきなり、自己相関(Autocorrelation)と偏自己相関(Partial Autocorrelation)を求めます。
以下、コードです。
# グラフを表示する領域と2つのサブプロットのセットを作成
fig, axes = plt.subplots(2, 1, figsize=(12, 12))
# ACFを計算し、1つ目のサブプロットにプロット
plot_acf(data, lags=40, ax=axes[0])
axes[0].set_title('Autocorrelation Function (ACF)') # Set the title
axes[0].grid(True) # Display the grid lines
# PACFを計算し、2つ目のサブプロットにプロット
plot_pacf(data, lags=40, method='ywm', ax=axes[1])
axes[1].set_title('Partial Autocorrelation Function (PACF)') # Set the title
axes[1].grid(True) # Display the grid lines
# プロットを表示
plt.tight_layout()
plt.show()
fig, axes = plt.subplots(2, 1, figsize=(12, 12)):plt.subplots()関数を使用して新しいfigureを作成し、その中に2つのサブプロットを配置します。引数の2, 1は、2行1列のサブプロットを作成することを示しています。figsize=(12, 12)は、figureのサイズを幅12インチ、高さ12インチに設定します。この関数はfigureオブジェクトとサブプロットのaxesオブジェクトの配列を返します。plot_acf(data, lags=40, ax=axes[0]):plot_acf()関数を使用してACFを計算し、その結果を最初のサブプロット(axes[0])にプロットします。axes[0].set_title('Autocorrelation Function (ACF)'): 最初のサブプロットのタイトルを設定します。axes[0].grid(True): 最初のサブプロットにグリッド線を表示します。plot_pacf(data, lags=40, method='ywm', ax=axes[1]):plot_pacf()関数を使用してPACFを計算し、その結果を2つ目のサブプロット(axes[1])にプロットします。axes[1].set_title('Partial Autocorrelation Function (PACF)'): 2つ目のサブプロットのタイトルを設定します。axes[1].grid(True): 2つ目のサブプロットにグリッド線を表示します。plt.tight_layout(): グラフのレイアウトを自動的に調整します。これにより、サブプロット間のスペースが適切に設定され、ラベルやタイトルが重ならないようになります。plt.show(): プロットを表示します。これまでのプロット設定を適用し、結果のグラフを表示します。
以下、実行結果です。
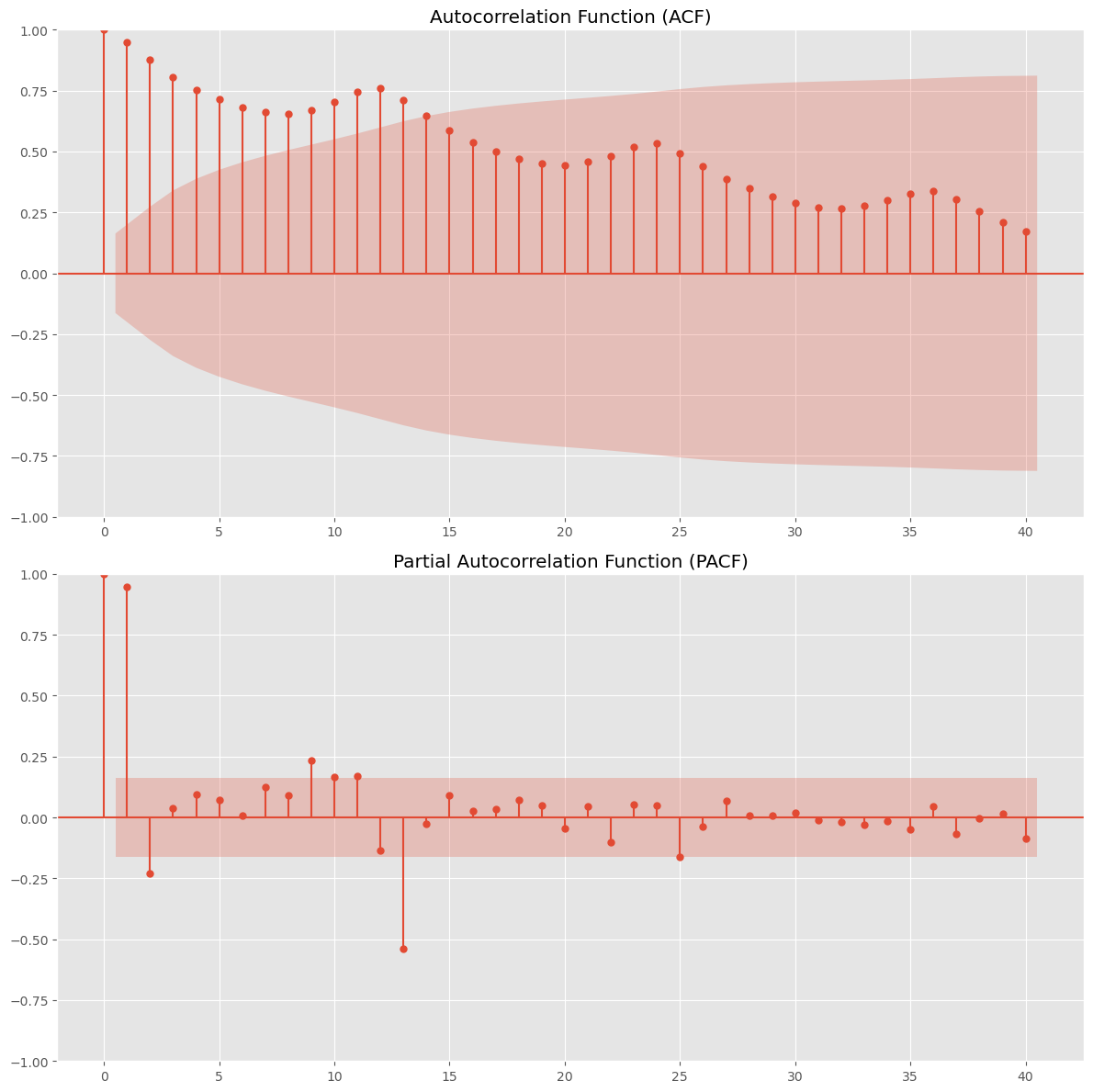
ACFプロット
各ラグ(遅延)における自己相関を示します。y軸は自己相関の値(-1から1)を、x軸はラグの値(通常、時間の単位)を示します。各棒の高さはそのラグにおける自己相関の大きさを示し、棒が信頼区間(背景が薄い赤の領域)を超えている場合、そのラグの自己相関は統計的に有意であると解釈されます。
PACFプロット
他のラグが制御されたときの各ラグ間の相関を示します。これは、時系列の特定のラグが他のラグを通じてではなく、直接的に前の観測値に影響を与える程度を測定します。
何となく、ACFプロットからラグ12、24、36、…と自己相関が高くなっていることが伺えますが、明確でありません。
トレンド成分が邪魔しているようです。
トレンド非定常性を除去した場合
トレンド非定常性の除去をした時系列データに対し、自己相関分析を実施する場合です。
自己相関(Autocorrelation)と偏自己相関(Partial Autocorrelation)を求める前に、トレンド非定常性の除去をします。
以下、コードです。
# データのトレンド非定常性を除去するために、最初の差分を取る
data_diff = data.diff().dropna()
# 差分を取った時系列データをプロット
plt.figure(figsize=(12, 6))
plt.plot(data_diff)
plt.title('Differenced Air Passengers Over Time')
plt.grid(True)
plt.show()
data_diff = data.diff().dropna():diff()関数を使用して時系列データの最初の差分を取ります。差分を取ると、各時点での値が前の時点からどれだけ変化したかを示す新しい時系列が得られます。これにより、データのトレンド(時間とともに増加または減少する傾向)が除去され、データが定常になることが多いです。dropna()関数を使用して、差分を取ることで生じるNaN値を削除します。結果はdata_diffという変数に保存されます。plt.figure(figsize=(12, 6)): 新しいfigureを作成し、そのサイズを幅12インチ、高さ6インチに設定します。plt.plot(data_diff):data_diffのプロットを作成します。x軸はデータのインデックス(この場合は年月)を、y軸は旅客数の変化量を表しています。plt.title('Differenced Air Passengers Over Time'): プロットのタイトルを設定します。タイトルは’Differenced Air Passengers Over Time’となります。plt.grid(True): グリッド線をプロットに表示します。plt.show(): プロットを表示します。これまでのプロット設定を適用し、結果のグラフを表示します。
以下、実行結果です。
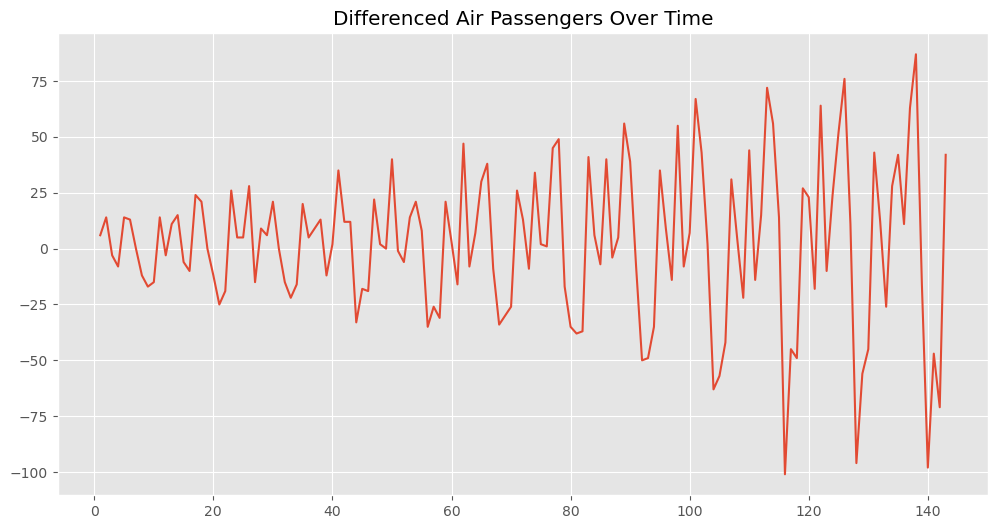
元の時系列データからトレンドが除去された新しい時系列データが得られました。これにより、データの季節性や他のパターンをより明確に視覚化できます。
このトレンド非定常性の除去をした時系列データに対し、自己相関(Autocorrelation)と偏自己相関(Partial Autocorrelation)を求めます。
以下、コードです。
# グラフを表示する領域と2つのサブプロットのセットを作成
fig, axes = plt.subplots(2, 1, figsize=(12, 12))
# ACFを計算し、1つ目のサブプロットにプロット
plot_acf(data_diff, lags=40, ax=axes[0])
axes[0].set_title('Autocorrelation Function (ACF) of Differenced Data') # Set the title
axes[0].grid(True) # Display the grid lines
# PACFを計算し、2つ目のサブプロットにプロット
plot_pacf(data_diff, lags=40, method='ywm', ax=axes[1])
axes[1].set_title('Partial Autocorrelation Function (PACF) of Differenced Data') # Set the title
axes[1].grid(True) # Display the grid lines
# プロットを表示
plt.tight_layout()
plt.show()
fig, axes = plt.subplots(2, 1, figsize=(12, 12)):plt.subplots()関数を使用して新しいfigureを作成し、その中に2つのサブプロットを配置します。引数の2, 1は、2行1列のサブプロットを作成することを示しています。figsize=(12, 12)は、figureのサイズを幅12インチ、高さ12インチに設定します。この関数はfigureオブジェクトとサブプロットのaxesオブジェクトの配列を返します。plot_acf(data_diff, lags=40, ax=axes[0]):plot_acf()関数を使用して差分を取ったデータのACFを計算し、その結果を最初のサブプロット(axes[0])にプロットします。axes[0].set_title('Autocorrelation Function (ACF) of Differenced Data'): 最初のサブプロットのタイトルを設定します。axes[0].grid(True): 最初のサブプロットにグリッド線を表示します。plot_pacf(data_diff, lags=40, method='ywm', ax=axes[1]):plot_pacf()関数を使用して差分を取ったデータのPACFを計算し、その結果を2つ目のサブプロット(axes[1])にプロットします。axes[1].set_title('Partial Autocorrelation Function (PACF) of Differenced Data'): 2つ目のサブプロットのタイトルを設定します。axes[1].grid(True): 2つ目のサブプロットにグリッド線を表示します。plt.tight_layout(): グラフのレイアウトを自動的に調整します。これにより、サブプロット間のスペースが適切に設定され、ラベルやタイトルが重ならないようになります。plt.show(): プロットを表示します。これまでのプロット設定を適用し、結果のグラフを表示します。
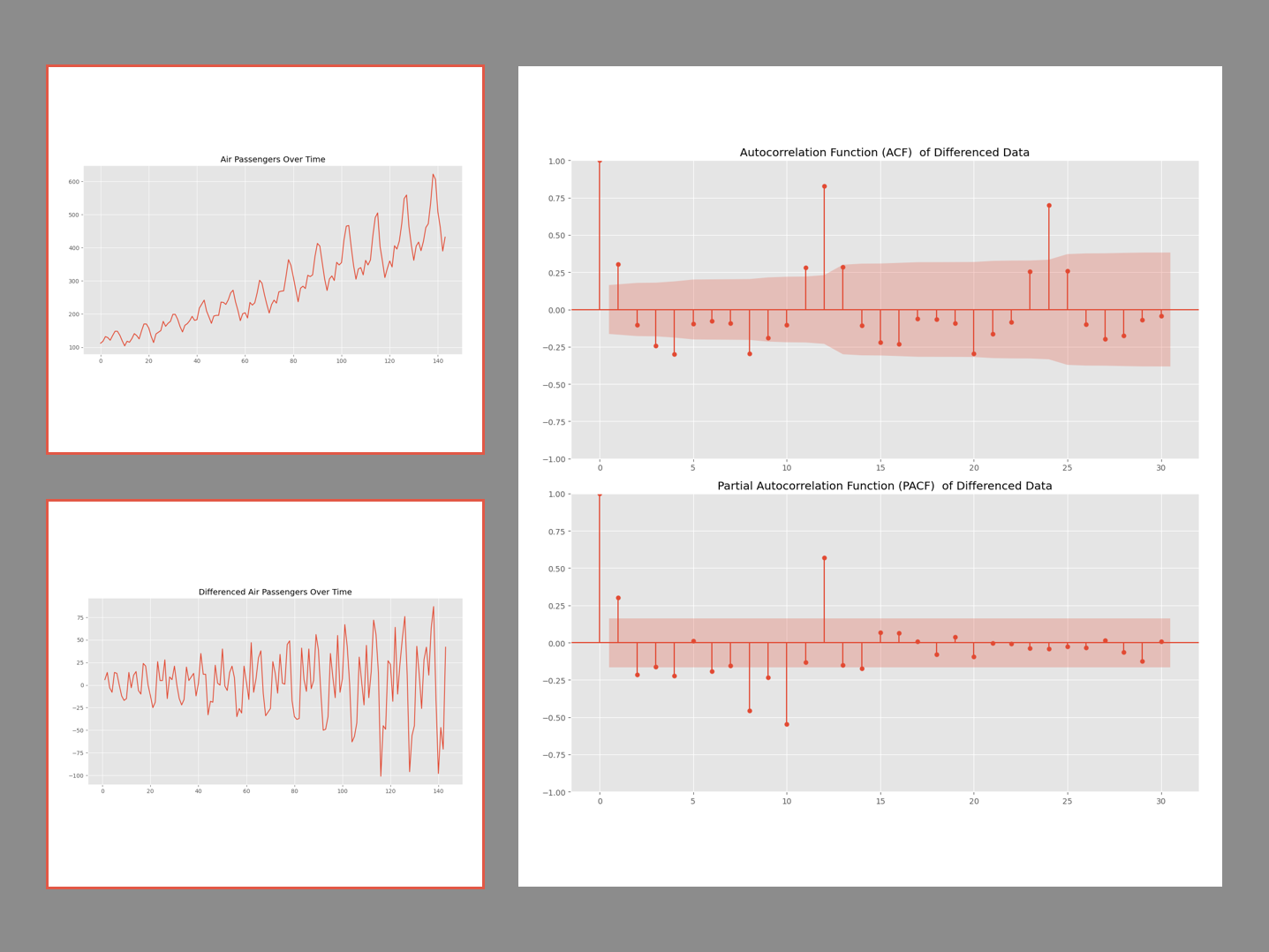
以下、実行結果です。
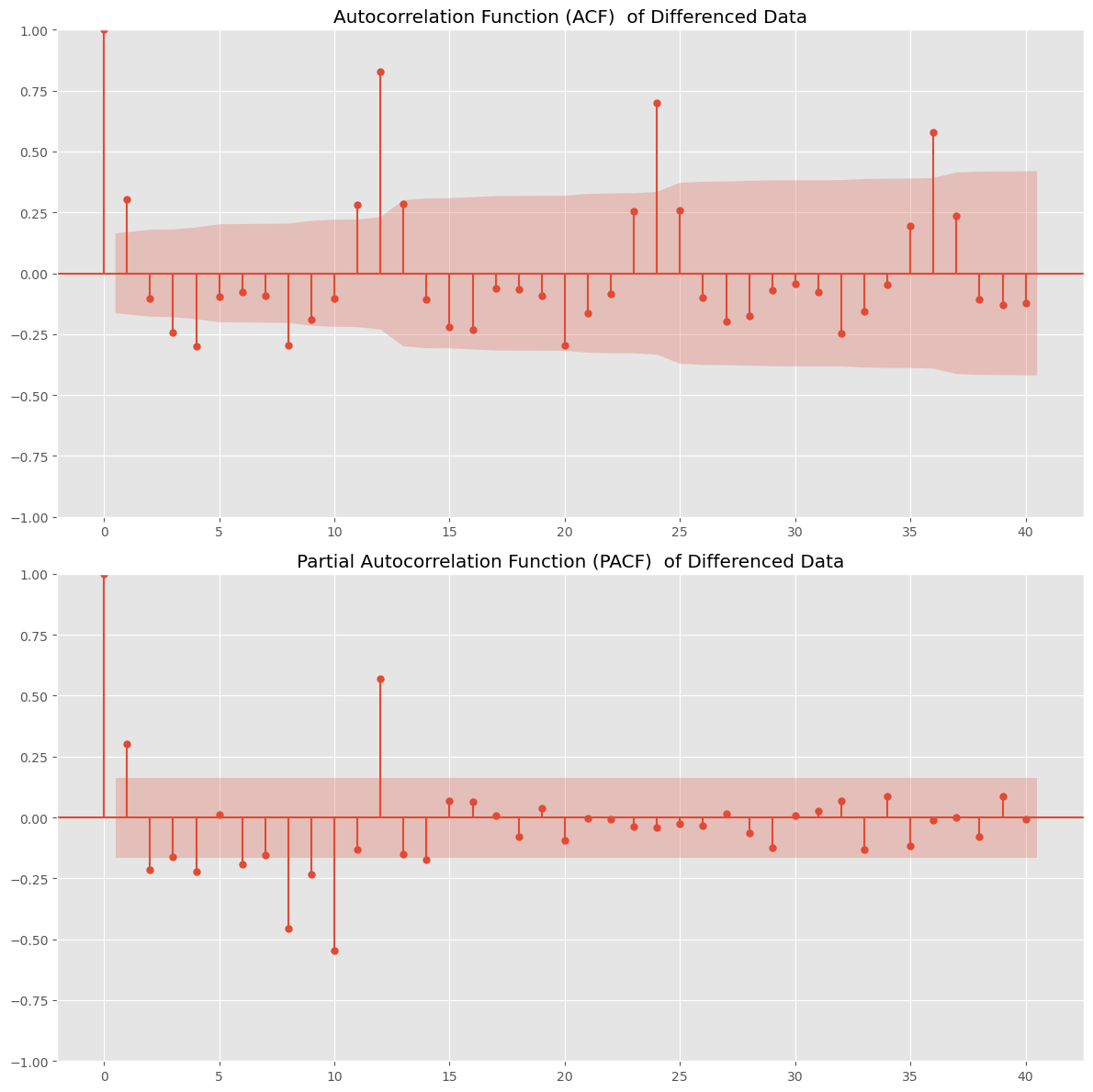
先ず、ACFプロットを見てみます。
ラグ12、24、36、…の自己相関が高いことが分かります。
季節性の周期は、12周期、24周期、36周期、…と複数あるかもしれません。
次に、PACFプロットを見てみます。
ラグ12の偏自己相関が高く、ラグ24、36、…の偏自己相関が小さいことが分かります。
要するに、季節性の周期は12周期である可能性が高いです。
まとめ
今回は、自己相関分析による周期の長さの見つけ方を説明しました。
ラグの相関係数を求めるだけでしたので、比較的分かりやすい方法かと思います。
次回は、スペクトル分析による周期期間の検出する方法を説明します。