時系列データの「定常性」と「3つの非定常性」

時系列データ関連のお勉強をしたときに、必ず登場する厄介な概念の1つが「定常性（Stationarity）」です。

定常性（Stationarity）は、時系列データの統計的な特性（平均、分散、自己相関など）が時間によらず一定であるという性質を指します。これは、時系列分析において重要な前提条件となる場合が多いです。

具体的には、定常性には以下のような特性があります。

平均が時間によらず一定: これはデータの「中心」が時間とともに変化しないことを意味します。つまり、ある時点での平均値が別の時点での平均値と同じであることを示します。
分散が時間によらず一定: これはデータの「ばらつき」が時間とともに変化しないことを意味します。つまり、ある時点での分散が別の時点での分散と同じであることを示します。
自己共分散（または自己相関）が時間によらず一定: これは2つの時点間の関連性がラグにのみ依存し、時間には依存しないことを示します。

意味わからん！ という方も少なくないと思いますが、誤解を恐れず簡単にいうと、その時系列データの構造が時間によって変化しない、ということです。

この時系列データの定常性は、そのデータを用いて行う多くの統計的モデリングや分析手法にとって重要な前提となります。

なぜでしょうか？

今回は、「時系列データの『定常性』と『3つの非定常性』」というお話しをします。

Contents

なぜ定常性が重要なのか？
3つの主な非定常性
定常かどうかの調べ方
主な定常化処理
非定常性の検知と、定常化処理
　順番
　サンプルデータ
　モジュールの読み込み
　データセットの読み込み
　定常かどうかを確認
　トレンド非定常性
　季節性非定常性
　分散非定常性
結局のところSARIMAモデル
まとめ

なぜ定常性が重要なのか？

時系列データの定常性は、そのデータを用いて行う多くの統計的モデリングや分析手法にとって重要な前提となります。

時系列データを用いた重要なタスクの一つに、将来予測というものがあります。

例えば、このような将来予測の際に一貫性を保つと仮定できると、予測しやすくなります。

一貫性を保つとは、その時系列データの特性（平均と分散など）が時間に依存せず一定であるという意味です。

この定常であるという仮定を過去だけでなく将来も続くと仮定することにより、その時系列データから得た知見やモデルは将来の予測に対しても一貫性を持つ（過去のデータのパターンが将来も同じように続く）とされるからです。

少なくとも、過去データすら定常でないデータが、将来定常であるとは仮定しにくいです。過去に定常であれば、近未来であればその定常性は保つと考え予測する、ということです。

予測の信頼性
定常性を持つデータでは、過去のデータから学習したモデルが将来も適用可能であると期待できます。なぜなら、そのデータの特性（平均や分散など）が一定であるため、過去のパターンが将来も続くという仮定が成り立つからです。このため、定常性を持つデータから学習したモデルは、将来の予測において信頼性を保つことが期待できます。

パラメータの一貫性
定常性を持つデータを用いてモデルを学習する場合、そのモデルのパラメータ推定値は一貫性を持つと言えます。一貫性とは、サンプルサイズが無限大に近づくとき、真のパラメータ値に収束するという性質を指します。この性質により、学習したモデルは信頼性の高い予測を提供することが期待できます。

非定常なデータをそのまま分析すると、データの特性が時間の経過とともに変化していくため、過去のデータに基づくモデルが将来的に有効であるという保証が得られません。このような理由から、時系列データ分析では一般的に、データを定常化してから分析を行います。

非定常な時系列データをそのまま分析すると、予測の信頼性の低下やモデルのパラメータ推定の不安定性など、いくつかの問題が生じる可能性があります。他には、見せかけの回帰（spurious regression）の問題が起こる可能性があります。

見せかけの回帰（Spurious regression）とは、2つの変数間に本質的な関連性がないにもかかわらず、統計的に有意な関連性が見られると誤って結論付けてしまう現象を指します。特に、非定常な時系列データを分析する際にこの問題が発生しやすいとされています。例えば、2つの非定常な時系列があり、それぞれが時間とともに増加する傾向にあるとします。これらの系列をそのまま回帰分析すると、系列間に強い正の相関があるように見えるかもしれません。しかし、これは見せかけの回帰となります。なぜなら、それぞれの系列が時間とともに増加する傾向があるだけで、それらが本質的に関連しているわけではないからです。

この問題を解決するための一つの方法は、データを定常化（例えば差分を取るなど）することです。これにより、見せかけの回帰の問題を避け、本当に変数間に関連性があるのかを適切に評価することが可能になります。

3つの主な非定常性

非定常性には主に以下の3つのタイプがあります。

トレンド非定常性: 平均が時間とともに変化する非定常性。差分を取ることで定常化を試みます。
季節性非定常性: 一定の周期を持つ季節変動に存在する非定常性。季節差分を取ることで定常化を試みます。
分散非定常性: 分散が時間とともに変化する非定常性。対数変換などを用いて定常化を試みます。

これらの非定常性は複数同時に存在することもあり、その場合にはそれぞれ適切な手法で定常化を試みます。

要するに、時系列データを手にしたら……

定常かどうかを調べる
非定常であれば定常化処理をする

……ということをします。

定常かどうかの調べ方

時系列データが定常性を満たしているかどうかを確認するためには、視覚的な分析と統計的な検定の二つの方法が一般的に用いられます。

視覚的な分析
データをプロットして視覚的に確認します。定常性を満たすデータは、時間に関して一定の平均（中心線が一定）と一定の分散（変動の幅が一定）を持つことが期待されます。

統計的な検定
定常性を確認するために、統計的な検定を行います。

主な検定手法は以下の2つです。

ディッキー-フラー検定（ADF検定）: ディッキー-フラー検定は、単位根検定の一つで、時系列データが非定常である（単位根を持つ）という帰無仮説を検定します。p値が一定の有意水準（例えば0.05）以下であれば、帰無仮説を棄却し、データが定常であると結論づけます。
KPSS検定（Kwiatkowski-Phillips-Schmidt-Shin検定）: KPSS検定は、ディッキー-フラー検定とは逆に、データが定常であるという帰無仮説を検定します。p値が一定の有意水準以上であれば、帰無仮説を採択し、データが定常であると結論づけます。

これらの統計的検定は、Pythonのstatsmodelsパッケージを用いて容易に行うことができます。

以上の方法を組み合わせて、データの定常性を確認します。視覚的な分析だけでなく統計的な検定も行うことで、より確実な判断が可能となります。

主な定常化処理

非定常であると検知された場合、定常化処理を実施します。

主な方法は次の通りです。

トレンド非定常性の定常化
差分取得：データの時点間での差分を取ることで、トレンドを除去します。一次差分（各時点の値とその前の時点の値との差）は、線形のトレンドを除去するのに有効です。二次差分（一次差分の差分）は、二次関数的な（曲線の）トレンドを除去するのに有効です。

季節性非定常性の定常化
季節差分：データに明確な季節パターンが存在する場合（例えば、毎年の夏に売上が上がるなど）、季節差分を取ることで季節性を除去します。データが季節的なトレンド（例えば、毎年の夏のピークが前年よりも高くなっている場合）を持っている場合、季節的差分を取ることでそのトレンドが緩和されます。季節差分は、各時点の値とその1周期前の時点の値との差を取ることです。

分散非定常性の定常化
データの分散が時間的に増加している場合、Box-Cox変換（対数変換を一般化した変換）適用すると分散が安定化します。Box-Cox変換は、データが正の値を取る場合に有効で、対数変換よりも柔軟な変換を提供します。

これらの方法は、データの特性に応じて適切に選択し組み合わせます。

なお、これらの変換を行った後には、データが定常になったかどうかを確認するために単位根テストなどの定常性のテストを行うことが重要です。

非定常性の検知と、定常化処理

　順番

非定常性の検出と定常化の適切な順番は、データの特性や目的による一部ではありますが、一般的なアプローチとしては以下の順序が推奨されます。

トレンド非定常性の確認と除去：まず初めにデータのトレンドを調査します。データがトレンド非定常性を示している場合、一次差分をとるなどしてトレンドを除去します。
季節性非定常性の確認と除去：トレンドが除去された後、季節性を確認します。季節性が存在する場合、季節差分を取るなどして季節パターンを除去します。
分散非定常性の確認と除去：トレンドと季節性が除去された後、最終的にデータの分散が一定かどうかを調査します。分散が時間的に変動する場合、対数変換やBox-Cox変換を行って分散を一定にします。

この順序で処理を行う理由は、トレンドや季節性はデータの全体的な構造を決定する重要な要素であるため、これらを先に取り扱うことでデータの細かい挙動に対する理解を深めることができ、より適切なモデル化を行うことが可能となるからです。

また、分散非定常性はこれらの大きな要素が除去された後により明確に見えてきます。

　サンプルデータ

時系列データの分析例でよく登場する「航空旅客データ」（AirPassengers）を使います。

航空旅客データは、国際航空旅客の月次データを指します。具体的には、1949年から1960年までの12年間の国際航空旅客数（単位: 1000人）を含む時系列データです。各データポイントは、その月の旅客数を示しています。

このデータセットは周期性（季節性）とトレンド（一般的に増加しています）の両方を含んでいます。特に、旅行の高シーズンやオフシーズンに対応する明確な季節的なパターンが見られます。このような特性から、航空旅客データは時系列分析の手法を学習したり、試したりするためのクラシックなデータセットとして広く使われています。

Pythonのstatsmodelsライブラリでは、このデータセットを’AirPassengers’という名前で取得することができます。このデータセットを使って、時系列分析の各種手法（例えば、移動平均、指数平滑、ARIMA、季節調整など）を試すことができます。

　モジュールの読み込み

先ず、必要なモジュールを読み込みます。特別なものは使っていません。

以下、コードです。

import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.seasonal import seasonal_decompose
from scipy.stats import boxcox

import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフのスタイル
plt.rcParams['figure.figsize'] = [12, 9] # グラフサイズ設定

pandasはデータフレームの操作やデータの読み込みに使用されるライブラリです。
numpyは数値演算や配列操作に使用されるライブラリです。
statsmodels.apiは統計モデルの構築や統計的推測に使用されるライブラリです。
statsmodels.tsa.stattoolsは時系列データの分析に使用される統計ツールを提供するモジュールです。
statsmodels.tsa.seasonalは季節性の分析に使用されるモジュールです。
scipy.statsは統計関数や確率分布の操作に使用されるライブラリです。
matplotlib.pyplotはグラフの描画に使用されるライブラリです。
plt.style.use('ggplot')はグラフのスタイルをggplotスタイルに設定しています。ggplotスタイルはRのggplot2パッケージのスタイルを再現したもので、美しいグラフを描画するための設定がされています。
plt.rcParams['figure.figsize'] = [12, 9]はグラフのサイズを設定しています。ここでは横幅12インチ、縦幅9インチのサイズを指定しています。

　データセットの読み込み

「航空旅客データ」（AirPassengers）のデータセットを読み込みます。

以下、コードです。

# データの取得
data = sm.datasets.get_rdataset('AirPassengers').data['value']

# データの可視化
data.plot()
plt.show()

以下、実行結果です。

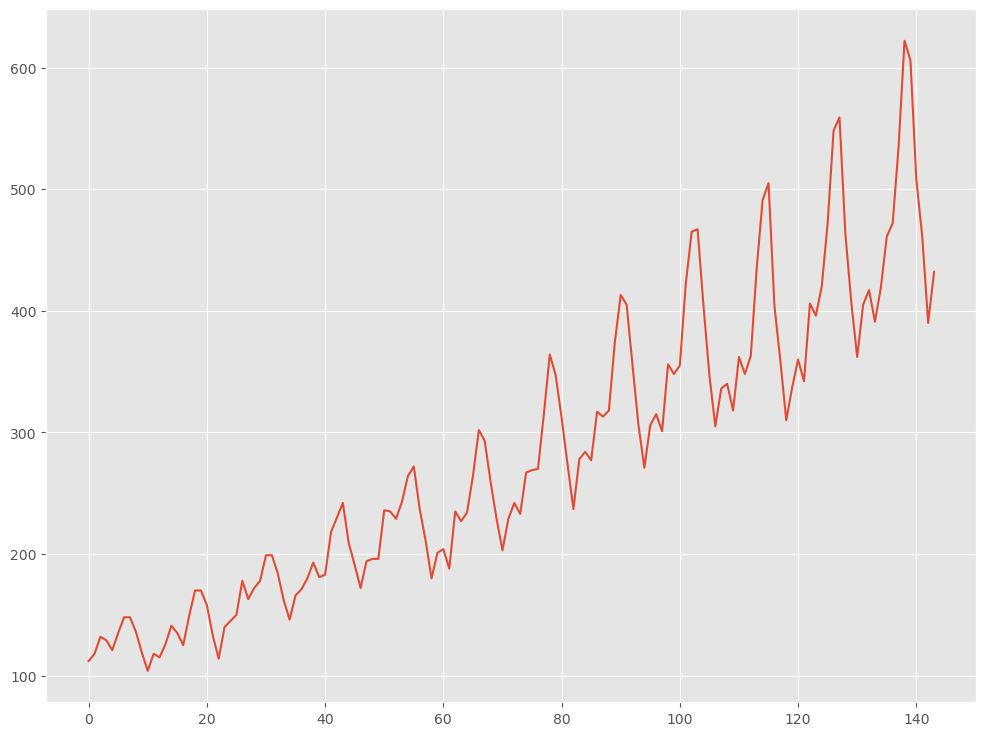
季節性とトレンドの両方を含んでいることが分かります。

また、データの振幅（要は、分散）がどんどん大きくなっているようにも見えます。ただ、この分散の変化は、他の非定常性処理で消える場合も多いです。

　定常かどうかを確認

ADF検定を実施し、この時系列データが単位根過程（非定常過程）であるかどうかを検定します。

ADF検定の結果は、検定統計量（ADF Statistic）とp値（p-value）として表示されます。

以下、コードです。

# ADF検定（単位根テスト）を実施
result = adfuller(data)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])

adfuller関数を使用して、dataという時系列データに対してADF検定を実施しています。
adfuller関数は、検定統計量、p値、使用されたラグの数などの結果を返します。結果はresultという変数に格納されます。
print関数を使用して、検定結果を表示しています。%fは浮動小数点数を表示するためのフォーマット指定子です。result[0]は検定統計量、result[1]はp値を示しています。

このコードの実行結果として、ADF検定の結果である検定統計量とp値が表示されます。

これにより、時系列データが定常過程（単位根を持たない）か非定常過程（単位根を持つ）かを判断することができます。

検定統計量が有意水準よりも小さく、p値が有意水準よりも小さい場合、単位根を持たない（定常）と結論付けることができます。

以下、実行結果です。

ADF Statistic: 0.815369
p-value: 0.991880

p値が0.05よりも大きいため非定常と見なし、トレンド除去を行います。

　トレンド非定常性

トレンド非定常性の除去です。

以下、コードです。

# 差分処理によるトレンド非定常性の除去
data_diff = data.diff().dropna()
data_diff.plot()
plt.show()

# ADF検定による再チェック
result = adfuller(data_diff)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])

まず、元のデータに対して1次階差を計算して差分を取ります。これにより、トレンド成分を除去し、定常性を取り戻します。diff()関数はデータの差分を計算し、dropna()関数は欠損値を取り除きます。結果はdata_diffという新しいデータフレームに格納されます。その後、差分をプロットして表示します。
次に、差分を取ったデータに対して再びADF検定を実施し、検定統計量とp値を表示します。これにより、差分を取った後のデータが定常過程であるかどうかを確認します。

以下、実行結果です。

ADF Statistic: -2.829267
p-value: 0.054213

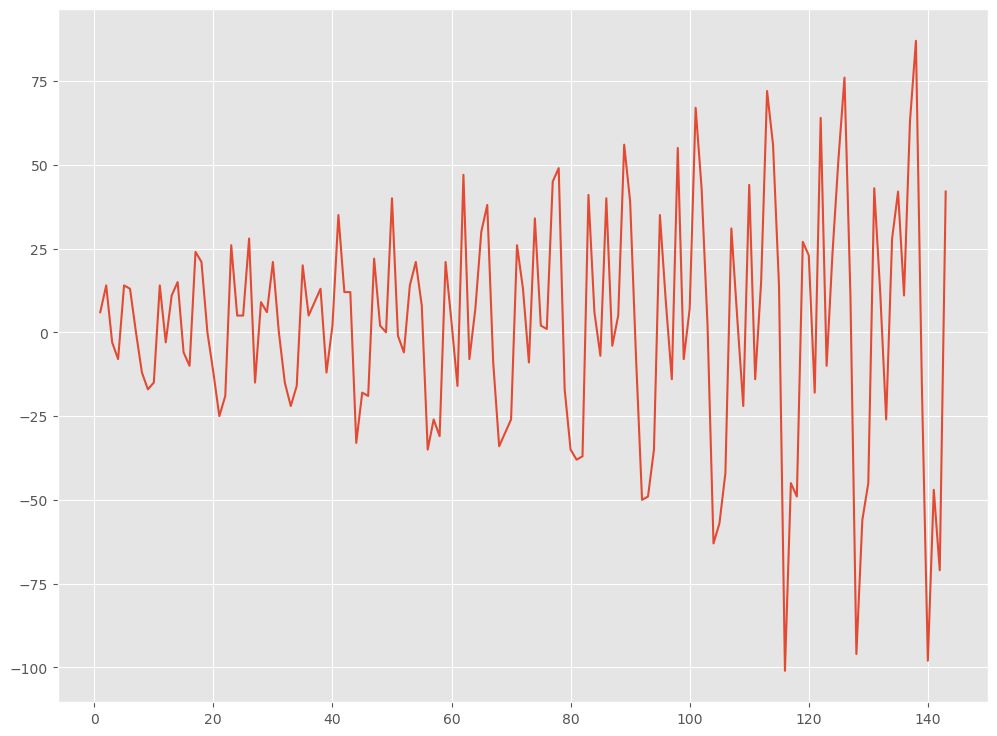
p値が0.05よりも大きいため非定常と見なし、季節性除去を行います。

　季節性非定常性

先ず、季節成分を抽出し見てみます。

以下、コードです。

# 季節成分の抽出
result = seasonal_decompose(data, period=12)

# 季節成分の可視化
result.seasonal.plot()
plt.show()

以下、実行結果です。

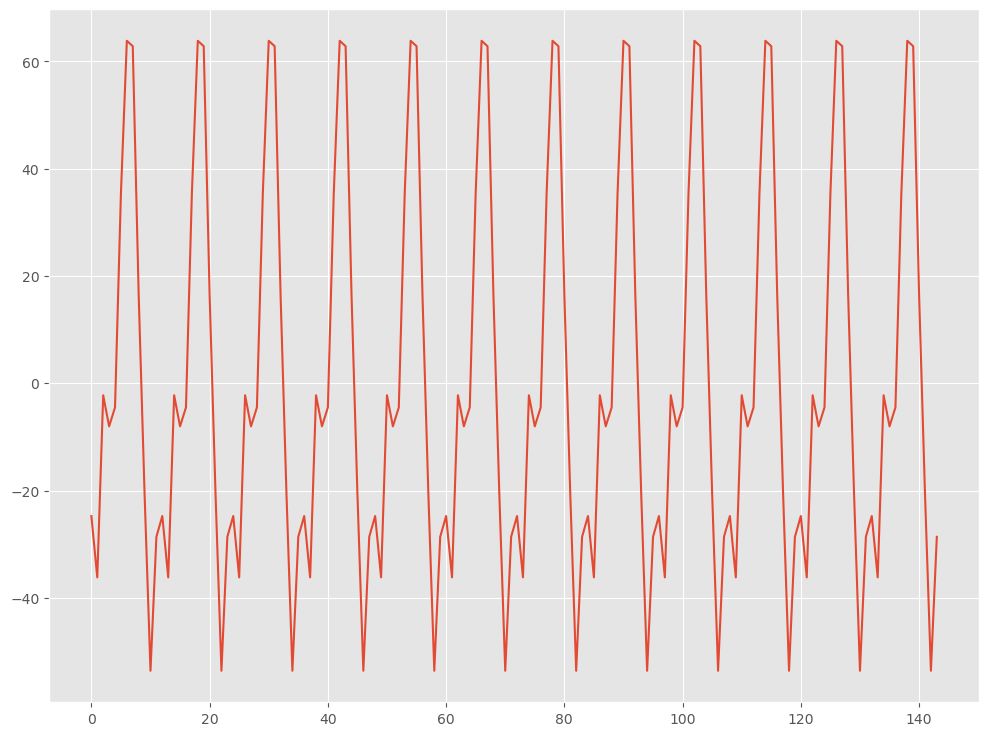
seasonal_decompose関数を使用して、時系列データから季節成分を抽出します。dataは元の時系列データであり、periodは季節周期を指定します。この関数は、元のデータからトレンド成分、季節成分、残差成分を分解して取得します。結果はresultというオブジェクトに格納されます。
抽出した季節成分をプロットして表示します。result.seasonalは抽出した季節成分のデータを示しており、それをplot関数でグラフ化します。最後にplt.show()でグラフを表示します。

では、季節非定常性の除去です。

以下、コードです。

# 季節差分をとって定常化
data_diff_s = data_diff.diff(12).dropna()
data_diff_s.plot()
plt.show()

# 季節性非定常性の検知と定常化後の再チェック
result = adfuller(data_diff_s)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])

data_diffは前のステップで取得したトレンド非定常性を除去したデータ（差分を取ったデータ）です。
diff(12)を使用して季節差分を計算し、12期間ごとの差分を取ります。dropna()を使用して欠損値を取り除きます。結果はdata_diff_sという新しいデータフレームに格納されます。その後、季節差分をプロットして表示します。
季節差分を取ったデータに対して再びADF検定を実施し、検定統計量とp値を表示します。これにより、季節差分を取った後のデータが定常過程であるかどうかを確認します。

以下、実行結果です。

ADF Statistic: -15.595618
p-value: 0.000000

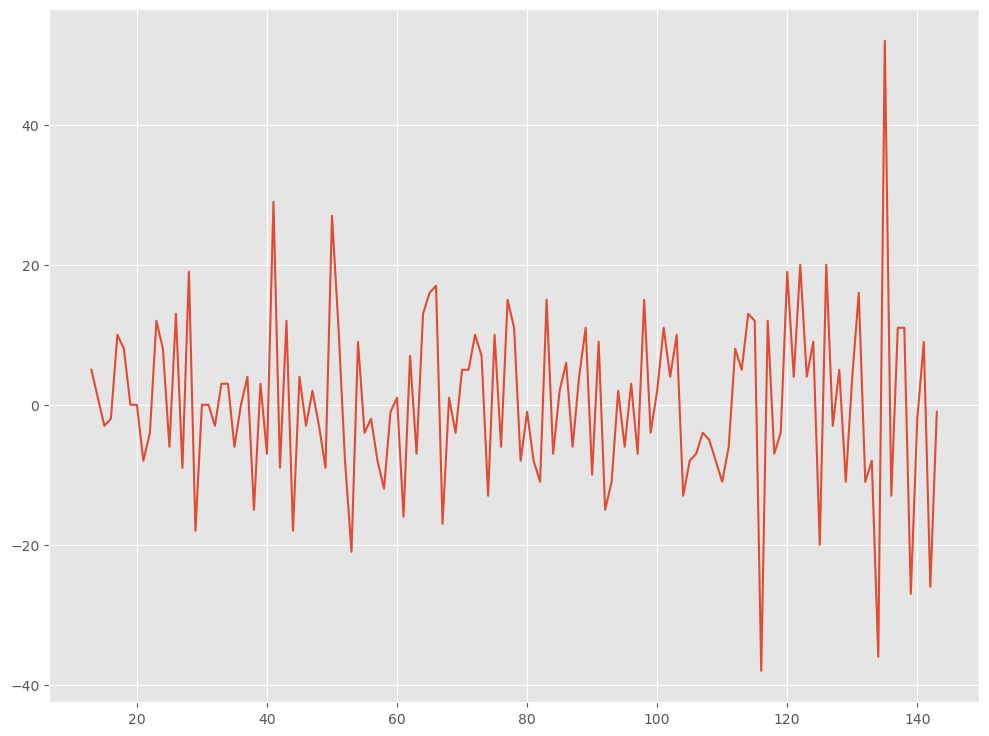
p値が0.05以下のため定常と見なし終了ですが、強引に分散非定常の除去を行います。

　分散非定常性

分散非定常性の除去です。

以下、コードです。

# データの最小値が0または負の場合、最小値を加算して正の値に変換
data_min = data_diff_s.min()
if data_min <= 0:
    data_diff_s = data_diff_s - data_min + 1

# Box-Cox変換で定常化
data_boxcox, _ = boxcox(data_diff_s)  # Box-Cox変換の結果とλの値を取得
data_boxcox = pd.Series(data_boxcox, index=data_diff_s.index)
data_boxcox.plot()
plt.show()

# 分散非定常性の検知と定常化後の再チェック
result = adfuller(data_boxcox)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])

まず、data_diff_sは前のステップで取得した季節差分を定常化したデータです。この部分では、データの最小値が0以下の場合に、最小値を加算して正の値に変換しています。これは、Box-Cox変換を適用するために必要な操作です。もし最小値が0以上であれば、変換は行われません。
boxcox関数を使用して、Box-Cox変換を適用します。data_diff_sを引数として与え、変換後のデータと変換パラメータ（λ）の値を取得します。変換後のデータはdata_boxcoxという変数に格納されます。その後、変換後のデータをプロットして表示します。
Box-Cox変換後のデータに対して再びADF検定を実施し、検定統計量とp値を表示します。これにより、Box-Cox変換後のデータが定常過程であるかどうかを確認します。

以下、実行結果です。

ADF Statistic: -15.599074
p-value: 0.000000

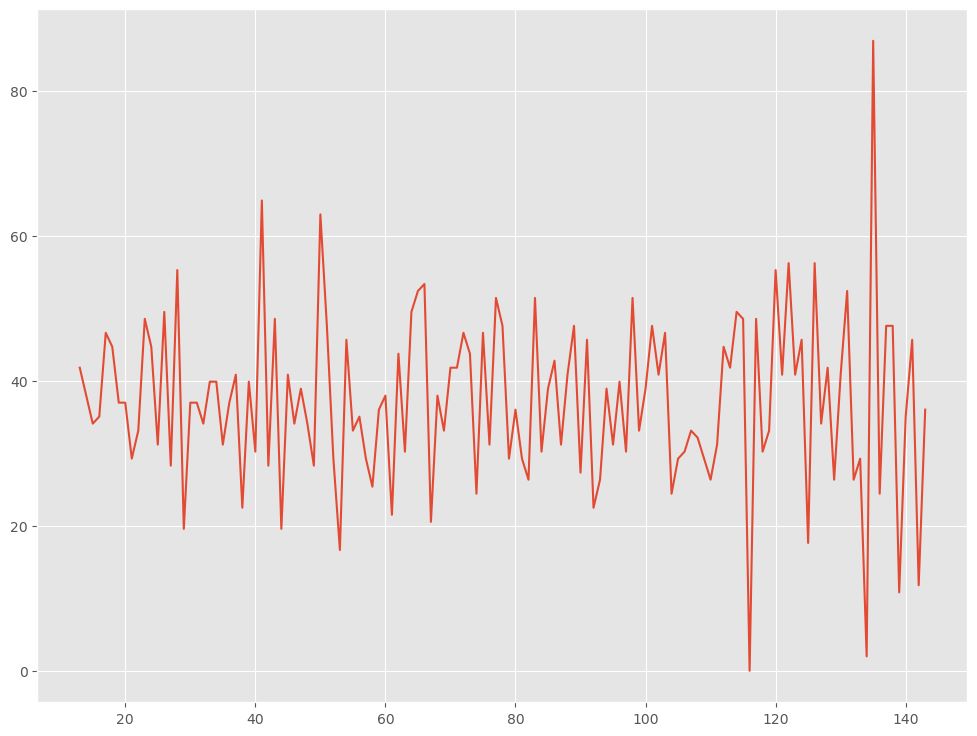
p値が0.05以下のため定常と見なします。

正直、分散非定常処理は不必要だったかもしれません。

元データは、データの振幅（要は、分散）がどんどん大きくなっているようにも見えましたが、分散非定常処理をすることなく、トレンド非定常処理と季節性非定常処理で十分でした。

結局のところSARIMAモデル

トレンド非定常性と季節非定常性を組み込んだ時系列モデルが、SARIMA（Seasonal Autoregressive Integrated Moving Average）モデルです。

古典的だが強力な時系列解析モデルで、実務的に一番よく利用され成果を出し続けているモデルです。実際、官庁統計などのマクロ指標などでも活用されています。

以下は、SARIMAモデルの概要です。

ARIMAモデルは、自己回帰成分（Autoregressive, AR）、和分（Integrated, I）、および移動平均成分（Moving Average, MA）からなります。これに対し、SARIMAモデルは季節成分（Seasonal, S）を追加することで季節性をモデル化します。SARIMAモデルは以下のパラメータで特徴づけられます:

1. p: 自己回帰次数（AR次数） – 直前の時点のデータの影響を表します。
2. d: 和分次数（I次数） – 差分（階差）を取る回数を表します。データが非定常である場合、定常性を持つ差分系列に変換します。
3. q: 移動平均次数（MA次数） – 直前の誤差項の影響を表します。
4. P: 季節自己回帰次数（季節AR次数） – 季節性の自己回帰成分を表します。
5. D: 季節和分次数（季節I次数） – 季節性の差分（階差）を取る回数を表します。
6. Q: 季節移動平均次数（季節MA次数） – 季節性の移動平均成分を表します。
7. s: 季節周期の長さ – 季節性の周期性を表します。

SARIMAモデルは、過去のデータのパターンと季節性を考慮して将来の値を予測することができます。モデルのパラメータはデータの性質に適合させる必要があります。SARIMAモデルのパラメータの推定には、自己相関関数（ACF）や部分自己相関関数（PACF）などのデータの自己相関を視覚化する統計手法が一般的に使用されます。

SARIMAモデルは季節性を持つ時系列データの予測やモデリングに広く使用され、需要予測、天候予測、金融データ分析などの様々な応用があります。

SARIMAの真ん中の和分「I」がトレンド非定常と季節性非定常の処理を担っています。

AutoARIMA（SARIMAモデルを自動構築）などの発展で、そのあたりの処理は自動化されています。

分散非定常性に関しては、どうしても気になる場合には、AutoARIMAとは別にBoxCox変換もしくは対数変換などで処理します。