Python SciPyで手を動かしながら学ぶ数理最適化
– 第1回: 数理最適化とは何か？ 基本概念の紹介 –

5398
Python SciPyで手を動かしながら学ぶ数理最適化– 第1回: 数理最適化とは何か？ 基本概念の紹介 –

数理最適化とは、複雑な問題を数学的に解く鍵となる一連の手法です。

この第1回目の記事では、数理最適化の魅力と重要性を探りながら、その基本概念や応用例を紹介します。線形最適化と非線形最適化の違いを明らかにし、数学と現実世界の架け橋となるこの領域の基礎を固めていきましょう。

さらに、SciPyを用いた具体的な問題解決のデモンストレーションを通じて、数理最適化がいかに強力なツールであるかを実感してください。

はじめに

私たちの日常生活からビジネスの意思決定に至るまで、最適な選択をすることは常に求められています。限られたリソースを最大限に活用し、最良の結果を導き出すためには、系統的な手法が必要です。このような背景から、数理最適化は非常に重要な役割を果たします。

数理最適化は、特定の制約条件下で目的関数を最大化または最小化する最適な解を見つける数学的な手法です。ビジネスにおいては、コスト削減、利益の最大化、生産プロセスの効率化など、様々な意思決定に活用されています。科学的研究や工学問題でも、複雑な問題を解決するための強力なツールとして利用されています。

この記事では、数理最適化の基本的な概念を紹介し、線形最適化と非線形最適化の違いについて解説します。さらに、Pythonの数値計算ライブラリであるSciPyを使った具体的な最適化問題の解法についても学んでいきます。

初心者にも理解しやすいように、基本的な定義から始め、徐々に応用例や実際の計算方法に進んでいく構成となっています。この記事を通じて、数理最適化の基礎知識を身につけ、実際にSciPyを使った問題解決ができるようになることを目指しています。

 

数理最適化の基本概念

数理最適化とは、特定の条件下で目的とする関数（目的関数）の値を最大化または最小化する変数の値を見つけ出す数学的手法です。

このプロセスは、複数の選択肢の中から最良の選択を定量的に判断するために使用されます。最適化問題は一般的に、目的関数、変数、制約から構成されます。

 

　適化問題の構成要素

目的関数
最適化の目標を数学的に表現した関数です。これを最大化または最小化することが最適化の目的です。

変数
最適化するために調整することができる値です。これらは目的関数の出力を決定する要因となります。

制約
変数が満たさなければならない条件です。これには等式制約や不等式制約が含まれ、問題の範囲や条件を定義します。

 

　最適化の具体的な応用例

数理最適化はビジネス、工学、科学、経済学など多岐にわたる分野で応用されています。具体的な例としては以下のようなものがあります。

  • 物流: 輸送コストを最小限に抑える最適な配送ルートの決定
  • 金融: 投資ポートフォリオのリスクとリターンのバランスを最適化
  • 製造: 生産コストを最小化しつつ、品質を保持するための生産プロセスの最適化
  • エネルギー管理: 需要と供給のバランスを取りながら、エネルギーコストを最小化

数理最適化は、これらのような複雑な問題に対して効率的で合理的な解を提供し、意思決定の質を高めるための強力なツールとなっています。

 

線形最適化と非線形最適化の違い

数理最適化の世界では、問題は大きく線形最適化と非線形最適化に分けられます。これらの違いを理解することは、適切な解法やアルゴリズムを選択するために重要です。

他には、整数最適化もしくは組合せ最適化というものもあります。一旦は、線形最適化と非線形最適化を取り上げます。

 

　線形最適化

線形最適化の特徴
線形最適化では、目的関数と全ての制約が線形関数で表されます。つまり、変数に対して1次式で表される形式を取ります。

適用シーン
資源配分、生産計画、輸送問題など、問題が比較的単純で直線的な関係にある場合。

メリット
計算が比較的簡単で、効率的なアルゴリズム（シンプレックス法や内点法など）が利用できる。

デメリット
実世界の複雑な問題を線形化することには限界があり、精度が落ちる場合がある。

 

　非線形最適化

非線形最適化の特徴
非線形最適化では、目的関数や制約の中に非線形関数が含まれます。これには多項式、対数、指数、三角関数などがあり、問題はより複雑になります。

適用シーン
エネルギーシステムの最適化、ロボティクス、機械学習のモデル調整など、複雑な関係性や非線形動態を持つ問題。

メリット
現実世界の複雑な関係をより正確に表現できる。

デメリット
計算が複雑で、求解時間が長くなったり、局所解に収束しやすい問題がある。

 

SciPyの導入と基本的な使い方

数理最適化を行うためには、適切なツールの選択が重要です。Pythonでの数理最適化には、SciPy（サイパイ）が広く利用されています。

 

　SciPyとは？

SciPyは、Pythonで科学計算を行うためのライブラリです。

数学、科学、工学分野での数値計算に特化しており、線形代数、微分方程式の解法、信号処理、画像処理、統計学、最適化など、幅広い機能を提供しています。

 

　インストール方法

SciPyはpipを使用して簡単にインストールできます。コマンドプロンプトやターミナルで以下のコマンドを実行してください。

pip install scipy

 

　基本的なモジュールと関数の紹介

SciPyには多くのサブモジュールがありますが、最適化に関連する主なモジュールはscipy.optimizeです。このモジュールには、最適化問題を解くためのさまざまな関数やクラスが含まれています。

  • minimize: 汎用的な最適化ソルバー。異なるアルゴリズムを指定できる。
  • linprog: 線形計画問題を解くための関数。
  • differential_evolution: 大域的最適化のための遺伝的アルゴリズム。

これらの関数を使用するには、目的関数、変数の初期値や範囲、制約などを適切に定義する必要があります。

 

簡単な例題を使ったSciPyのデモンストレーション

SciPyの基本的な使い方を理解するために、簡単な例題を用いたデモンストレーションを行います。

 

　例題の説明

例として、以下の線形計画問題を考えます。

目的関数：
\displaystyle \text{maximize } z=x+2y

制約条件：
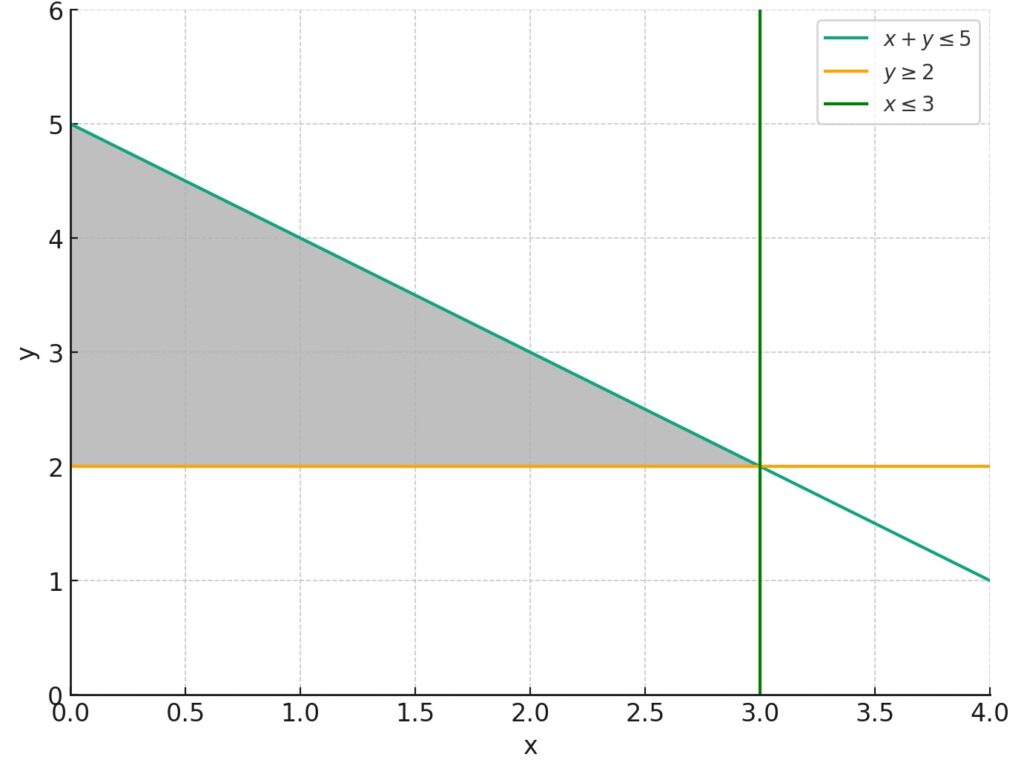
\displaystyle \begin{matrix} x+y \le 5 \\ x \le 3 \\ y \ge 2 \\ x,y \ge 0\end{matrix}

この問題では、制約条件のもとでzを最大化するxとyの値を求めます。

 

　SciPyを使った問題の定式化

まず、SciPyのlinprog関数を使用して問題を定式化します。linprogは最小化問題を解くために設計されているため、目的関数の符号を変更して最小化問題として扱います。

from scipy.optimize import linprog

# 目的関数の係数（最小化のために符号を反転）
c = [-1, -2]

# 制約条件の左辺
A = [[1, 1], [1, 0], [0, -1]]

# 制約条件の右辺
b = [5, 3, -2]

# 範囲条件（x, y >= 0）
x_bounds = (0, None)
y_bounds = (0, None)

# linprog関数を使用して問題を解く
res = linprog(
    c, 
    A_ub=A, b_ub=b, 
    bounds=[x_bounds, y_bounds], 
    method='highs'
    )

 

  • from scipy.optimize import linprog: SciPyライブラリからlinprog関数をインポートする。
  • c = [-1, -2]: 目的関数の係数を定義する。ここでは、最小化を行うために係数の符号を反転している。
  • A = [[1, 1], [1, 0], [0, -1]]: 制約条件の左辺の係数を行列として定義する。
  • b = [5, 3, -2]: 制約条件の右辺の値をベクトルとして定義する。
  • x_bounds = (0, None), y_bounds = (0, None): 変数の範囲を定義する。ここでは、xとyが非負であることを指定している（0以上）。
  • res = linprog(c, A_ub=A, b_ub=b, bounds=[x_bounds, y_bounds], method='highs'): linprog関数を使用して線形最適化問題を解く。A_ubとb_ubは不等式制約を表し、boundsは変数の範囲を指定する。method='highs'は使用するソルバーのタイプを指定している。

 

　ソルバーの実行と結果の解釈

上記のコードを実行すると、最適化問題の解が得られます。結果はresオブジェクトに格納されます。

print(res)

 

以下、実行結果です。

          con: array([], dtype=float64)
crossover_nit: 0
        eqlin:  marginals: array([], dtype=float64)
     residual: array([], dtype=float64)
          fun: -10.0
      ineqlin:  marginals: array([-2., -0., -0.])
     residual: array([0., 3., 3.])
        lower:  marginals: array([1., 0.])
     residual: array([0., 5.])
      message: 'Optimization terminated successfully. (HiGHS Status 7: Optimal)'
          nit: 0
        slack: array([0., 3., 3.])
       status: 0
      success: True
        upper:  marginals: array([0., 0.])
     residual: array([inf, inf])
            x: array([0., 5.])

 

  • con: 等式制約（equality constraints）に関連する情報。ここでは等式制約はないため、空の配列が返されています。
  • crossover_nit: クロスオーバー（高次の手法に移行する過程）のイテレーション数。この場合は0。
  • eqlin: 等式制約に関連する情報。ここでは空です。
  • fun: 最適化された目的関数の値。この場合、最小値は -10.0 です。符号を反転していたので、最大値は 10 です。
  • ineqlin: 不等式制約（inequality constraints）に関連する情報。marginalsはラグランジュ乗数、residualは残余です。
  • lower: 下限に関する情報。marginalsはラグランジュ乗数、residualは残余です。
  • message: 最適化の結果に関するメッセージ。ここでは「最適化が正常に終了した」とされています。
  • nit: 最適化のためのイテレーション数。ここでは0。
  • slack: 不等式制約のスラック変数の値。
  • status: 最適化の終了ステータス。0は成功を意味します。
  • success: 最適化が成功したかどうか。Trueは成功を意味します。
  • upper: 上限に関する情報。marginalsはラグランジュ乗数、residualは残余です。
  • x: 最適化問題の解。この場合、, y=5 が解です。

 

この出力には、最適な目的関数の値、解の状態、および変数xとyの最適な値が含まれます。

このシンプルな例では、解は直感的に理解しやすいですが、より複雑な問題では解の妥当性を検証するための追加的な分析が必要になる場合があります。

次回の「第2回: 線形最適化の基礎」でもう少し詳しく線形最適化について扱います。

 

まとめ

この記事では、数理最適化の基本的な概念とその重要性について学びました。数理最適化の基本構成要素である目的関数、制約、変数の役割を理解し、線形最適化と非線形最適化の違いについて考察しました。また、SciPyライブラリの導入と基本的な使い方を紹介し、実際の例題を用いてSciPyを使用した問題解決のデモンストレーションを行いました。

次回の記事では、線形最適化に焦点をあてます。

線形最適化の基本的な理論
ここでは、線形最適化がどのような理論的基盤に基づいているのかを探ります。シンプレックス法や線形計画法の基礎に触れ、線形最適化がどのように機能するのかを理解します。

制約と目的関数の設定方法
任意の線形最適化問題の核心は、適切な制約と目的関数の設定にあります。実際の問題をどのように数学的なモデルに変換するかを学びます。

SciPyを用いた線形最適化問題の解
SciPyライブラリを使用して線形最適化問題をどのように解くかを詳しく解説します。具体的なコード例を用いて、SciPyの機能を最大限に活用する方法を紹介します。

実例を通じた線形最適化の応用
最後に、実世界の問題を例にとり、線形最適化がどのように実用的な解を提供するかを見ていきます。リソース配分や生産計画など、さまざまな分野での応用例を取り上げます。

この次回の記事を通じて、線形最適化の基礎を固め、その実践的な応用能力を高めることができるでしょう。お楽しみに！

Python SciPyで手を動かしながら学ぶ数理最適化– 第2回: 線形最適化の基礎 –