線形最適化は、複雑な意思決定問題を数学的に定式化し、最適な解を見つけるための強力なツールです。
ビジネスの世界では、資源が限られている中で最大の利益を得る方法を見つける必要があります。また、工学の分野では、与えられた条件下で最適な設計を求めることが求められます。これらの課題は、線線形最適化を用いて解決することが可能です。
本講座の第2回では、線形最適化の基本的な理論、その数学的な構造、そして実世界の問題への適用方法について学んでいきます。
初歩から始めて、最終的にはPythonを用いた実践的な問題解決に進むことで、線形最適化の力強さと柔軟性を理解することができるでしょう。実業務で直面する多様な課題に対して、線形最適化がどのようにして有効な解を提供するのかを一緒に学んでいきましょう。
Contents
はじめに
数理最適化の分野では、問題を数学的に定式化し、その最適な解を見つけ出すことが目標です。前回、我々は数理最適化の基本概念とScyPyを使用した基本的な問題解決の手順を学びました。今回のセッションでは、より具体的に線形最適化の世界に焦点を当てます。
線形最適化は、数理最適化の中でも特に重要な分野であり、実世界の多くの問題に応用されています。物流、製造、金融、エネルギー管理など、幅広い分野で線形最適化の技術が利用されています。しかし、その基本原理と適用方法を理解することが、これらの技術を有効に活用する鍵となります。
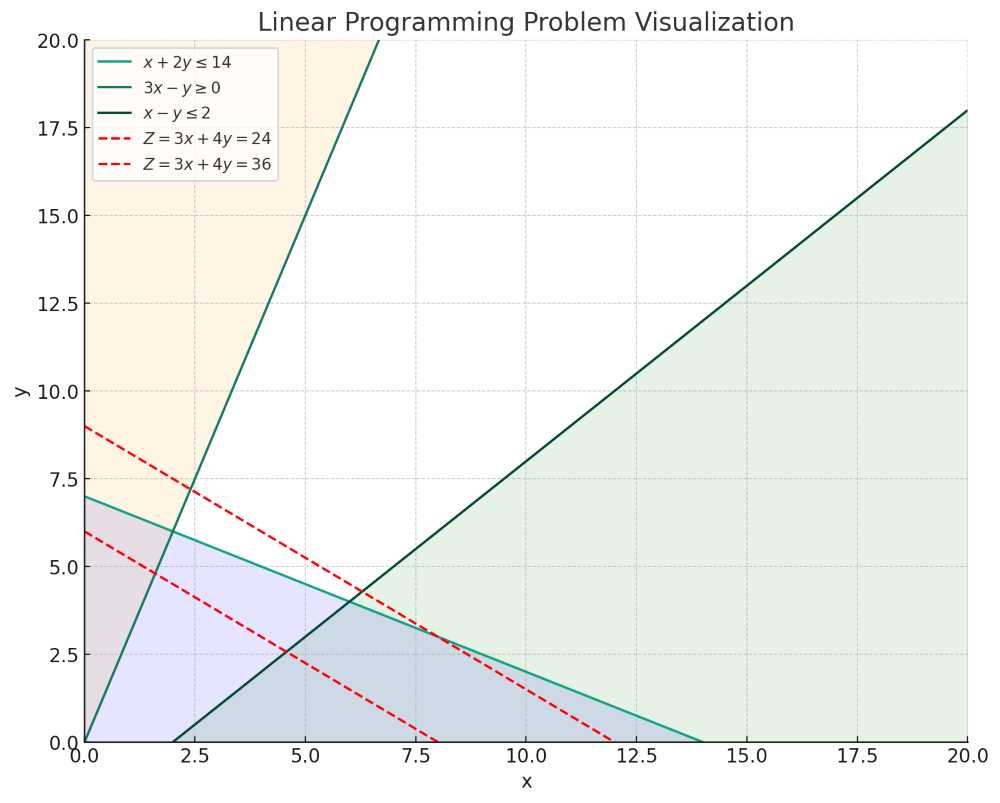
今回の記事の目標は、線形最適化の基本理論を理解し、実際にPythonのScyPyライブラリを使って問題を解く方法を学ぶことです。また、実例を通じて線形最適化がどのように応用されるかを見ていきます。
- 線形最適化の基本的な理論とその性質
- 目的関数と制約条件の設定方法
- ScyPyを使用した線形最適化問題の解法
- 実業務での線形最適化の応用例
線形最適化の基本理論
線形最適化の定義と基本的な性質
線形最適化、または線形計画法（Linear Programming, LP）とは、一連の線形関数の制約のもとで線形目的関数を最大化または最小化する問題です。ここでの「線形」という用語は、目的関数と制約がともに線形関数であることを意味します。つまり、これらの関数はその変数に関して1次式で表されます。
線形最適化の基本的な性質は以下の通りです。
- 解の存在: ある条件を満たす場合（可行領域が空でない場合）、線形最適化問題は解を持ちます。
- 凸性: 線形最適化問題の可行領域は凸集合です。これは、最適解が境界上または頂点に存在することを意味します。
- 最適解の一意性: ある条件下で、線形最適化問題は一意の解を持ちますが、複数の最適解が存在する場合もあります。
目的関数と制約の線形性の意義
目的関数と制約が線形であることの重要性は以下の点にあります。
- 単純さと効率性: 線形関数は計算が容易で、大規模な問題でも効率的に解くことが可能です。
- 解析の容易さ: 線形システムは理論的によく理解されており、解の特性や構造を分析しやすいです。
- 広範な応用: 多くの実世界の問題は、線形の枠組みで近似することができます。これにより、線形最適化は様々な分野で応用されています。
制約と目的関数の設定
目的関数の設定方法
線形最適化問題において、目的関数は解きたい問題の目標を数学的に表現するものです。これは通常、最大化または最小化したい量を線形関数として表します。
目的関数の設定には以下の点が重要です。
- 目標の明確化: 何を最適化したいのか、どのような結果を期待しているのかをはっきりさせます。
- 線形表現: 目的を線形関数として表現します。すなわち、目的変数の線形結合として表されるべきです。
- 係数の決定: 各変数の重要度や寄与度を反映する係数を適切に設定します。
制約条件の種類と設定方法
制約条件は、変数が満たすべき要件や制限を定義します。
線形最適化では主に以下の種類の制約があります。
- 等式制約（Equality constraints）: 変数の線形結合が特定の値に等しいことを要求します。
- 不等式制約（Inequality constraints）: 変数の線形結合が特定の値以下または以上であることを要求します。
- 非負制約（Non-negativity constraints）: すべての変数が非負であることを要求します。
制約の設定には以下のポイントが重要です。
- 現実的な制約の設定: 制約は問題の現実的な状況を反映するものである必要があります。
- 線形表現の使用: 制約も目的関数と同様に線形関数で表現されるべきです。
- 可解性の確保: 制約が矛盾していないこと、そして可解な領域を持つことを確認します。
実践的なヒントと注意点
線形最適化問題を設定する際には、以下のヒントと注意点を考慮に入れると良いでしょう。
- シンプルさを保つ: 問題を複雑にし過ぎないように注意します。必要最小限の変数と制約を使用することが重要です。
- モデリングの精度: 問題を線形化する際に、現実をどの程度正確に表現できるかを検討します。完璧な表現は難しい場合が多いので、妥協点を見つける必要があります。
- 数値的安定性: 係数や制約が極端に大きい値または小さい値を取らないようにします。数値的に不安定な問題は、解くのが困難になる可能性があります。
ScyPyを使った線形最適化問題の解法
線形最適化問題を解くための効率的かつ実用的なツールの一つが、Pythonの科学計算ライブラリであるScyPyです。ここでは、ScyPyを使って線形最適化問題をどのようにモデル化し、解くかについて詳しく見ていきましょう。
ScyPyにおける線形最適化問題のモデル化
ScyPyでは、linprog関数を用いて線形最適化問題を解くことができます。まずは、目的関数の係数、制約条件、変数の範囲などのパラメータを定義します。
今、次のような最小化問題を考えたとします。
目的関数：
\displaystyle \text{minimize } 1 \times x_1 + 2 \times x_2 + 3 \times x_3
制約条件：
\displaystyle \begin{matrix} -1 \times x_1 + 1 \times x_2 \le 1 \\ 1 \times x_1 + 1 \times x_3 \le 2 \\ x_1,x_2,x_3 \ge 0 \end{matrix}
ベクトルと行列で表現すると以下のようになります。
目的関数：
\displaystyle \text{minimize } \begin{bmatrix}1 & 2 & 3 \end{bmatrix}\begin{bmatrix}x1 \\ x2 \\ x3 \end{bmatrix}
制約条件：
\displaystyle \begin{array}{rr} \begin{bmatrix}-1 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \le \begin{bmatrix} 1 \\ 2 \end{bmatrix} \\ \\ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \ge \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \end{array}
この問題をコードにすると、以下のようになります。
import scipy.optimize as opt # 目的関数の係数（ここでは最小化問題を例とする） c = [1, 2, 3] # 不等式制約（Ax <= bの形式） A = [[-1, 1, 0], [1, 0, 1]] b = [1, 2] # 変数の範囲（例えば全ての変数が非負である場合） x_bounds = (0, None) # 問題の解決 result = opt.linprog(c, A_ub=A, b_ub=b, bounds=x_bounds)
linprog関数の使用方法とオプション
linprog関数は複数のパラメータを受け取ります。
c: 目的関数の係数ベクトル。A_ub: 不等式制約の係数行列（A）。b_ub: 不等式制約の右辺ベクトル（b）。A_eqとb_eq: 等式制約（Ax = bの形式）に使用。bounds: 各変数の範囲を指定。
また、methodパラメータを用いて、解法のアルゴリズムを指定することも可能です。デフォルトではhighsが使用されますが、他にsimplexやinterior-pointなどがあります。
解の解釈と分析
linprog関数の実行結果として返されるオブジェクトには、解に関する多くの情報が含まれています。
x: 最適解の変数値。fun: 最適解における目的関数の値。success: 問題が解けたかどうかのブール値。message: 解決過程や結果に関するメッセージ。
実行結果である最適解を出力するときには、例えば以下のようなコードで見ることができます。
if result.success:
print("最適解:", result.x)
print("目的関数の値:", result.fun)
else:
print("問題は解けませんでした。", result.message)
線形最適化の実践的応用例
線形最適化は理論的に興味深いだけでなく、実業務においても非常に役立つツールです。この章では、実業務での応用事例、実践的な問題への適用方法、および成功事例の分析を行います。
例えば、以下はビジネスでよくある事例です。
リソースの割り当て問題
企業が限られたリソースをいかに効率的に分配するかを決定する際、線形最適化は重要な役割を果たします。例えば、生産ラインの作業員や機械の割り当て、または予算配分などです。
輸送と物流問題
物流業界において、商品をコスト効率よく、迅速に配送するための最適なルートを決定することが求められます。線形最適化は、このようなルートの最適化に有効です。
ポートフォリオの最適化
金融分野において、リスクとリターンのバランスを考慮しながら、投資ポートフォリオを最適化する際に線形最適化が用いられます。
実践的な問題への適用方法
- 問題の定式化: 実際のビジネス問題を、目的関数、制約条件を含む線形最適化問題として定式化することが第一歩です。
- データの収集と処理: 問題を解くために必要なデータを収集し、適切に処理することが重要です。これには、データのクレンジングや前処理が含まれます。
- モデルの構築と解法の選択: ScyPyなどのツールを使って問題をモデル化し、最適な解法を選択します。
- 結果の分析と実装: 得られた解を分析し、実業務に適用可能かを評価します。必要に応じて、追加の調整や最適化を行うこともあります。
問題の定式化の例
リソースの割り当て問題
企業が限られたリソースをいかに効率的に分配するかを決定する問題
目的関数：
\displaystyle \text{maximize } \sum_{i=1}^{n} P_i x_i
制約条件：
\displaystyle \begin{array}{rrr} \sum_{i=1}^{n} R_{ij} x_i \le C_i \\ \\ x_i \ge 0 \end{array}
- n：製品の種類数
- P_i：製品iの利益
- x_i：製品iの生産量
- R_{ij}：製品iを1単位生産するのに必要なリソースjの量
- C_j：リソースjの利用可能な合計量
SciPyの最適化は、最小化問題として解くため、このような最大化問題の場合には、以下のように目的関数に -1 を掛けて最小化問題にします。
目的関数に -1 を掛けて最小化問題にする
\displaystyle \text{minimize } -1 \times \sum_{i=1}^{n} P_i x_i
輸送と物流問題
物流業界の最適なルートを決定する問題
目的関数：
\displaystyle \text{minimize } \sum_{i=1}^{m} \sum_{j=1}^{n} C_{ij} x_{ij}
制約条件：
\displaystyle \begin{array}{rrrrr} \sum_{i=1}^{m} x_{ij} = D_j \\ \\ \sum_{j=1}^{n} x_{ij} \le S_i \\ \\ x_{ij} \ge 0 \end{array}
- m: 出発地の数
- n: 目的地の数
- C_{ij}: 出発地 i から目的地 j への輸送コスト
- x_{ij}: 出発地 i から目的地 j への輸送量
- D_j: 目的地 j の需要量
- S_i: 出発地 i の供給量
ポートフォリオの最適化
金融分野の最適な投資ポートフォリオを求める問題
目的関数：
\displaystyle \text{maximize } \sum_{i=1}^{n} R_{i} x_{i}
制約条件：
\displaystyle \begin{array}{rrrrr} \sum_{i=1}^{n} x_{i} = 1 \\ \\ \sum_{i=1}^{n} K_i x_{i} \le T \\ \\ x_{i} \ge 0 \end{array}
- n：投資先の数
- R_i：資産先 i の期待リターン率
- x_i：投資先 i への投資比率
- K_i：投資先 i のリスク
- T：顧客のリスク許容度
この最大化問題も最小化問題として解くために、目的関数に -1 を掛けて最小化問題にします。
目的関数に -1 を掛けて最小化問題にする
\displaystyle \text{minimize } -1 \times \sum_{i=1}^{n} R_{i} x_{i}
事例１：リソースの割り当て問題
電子機器を製造するアルファ社は、2つの異なる製品（AとB）を生産しています。
企業には2種類のリソース（労働力と機械時間）があります。製品AとBを生産するためには、それぞれ異なる量のリソースが必要です。企業は限られたリソースを最も効率的に利用して、利益を最大化したいと考えています。
- 労働力: 100時間
- 機械時間: 80時間
- 製品Aの生産に必要な労働力: 1時間/単位
- 製品Aの生産に必要な機械時間: 0.5時間/単位
- 製品Bの生産に必要な労働力: 2時間/単位
- 製品Bの生産に必要な機械時間: 1時間/単位
- 製品Aの利益: 50ドル/単位
- 製品Bの利益: 100ドル/単位
定式化（ベクトルと行列で表現）すると以下のようになります。
目的関数：
\displaystyle \text{minimize } -1 \times \begin{bmatrix}50 & 100 \end{bmatrix}\begin{bmatrix}x1 \\ x2 \end{bmatrix}
制約条件：
\displaystyle \begin{array}{rrrrr} \begin{bmatrix}1 & 2 \\ 0.5 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \le \begin{bmatrix} 100 \\ 80 \end{bmatrix} \\ \\ \displaystyle x_{i} \ge 0 \end{array}
- x_1：製品Aの生産量
- x_2：製品Bの生産量
この問題をコードにすると、以下のようになります。
import numpy as np
import scipy.optimize as opt
# 利益係数
profit = [50, 100]
# 制約係数（労働力と機械時間）
constraints = [
[1, 2], # 労働力に関する制約
[0.5, 1] # 機械時間に関する制約
]
# 制約の右辺（利用可能な労働力と機械時間）
bounds = [100, 80]
# 問題の解決
result = opt.linprog(
c=-1 * np.array(profit), # 最大化のために係数を負にする
A_ub=constraints,
b_ub=bounds,
bounds=(0, None), # 製品の量は非負でなければならない
method='highs'
)
if result.success:
print("最適解:", result.x)
print("最大利益:", -1 * result.fun)
else:
print("最適化問題の解決に失敗しました。")
このコードは、与えられたリソース制約のもとで利益を最大化するための製品AとBの最適な生産量を計算します。linprog関数は線形最適化問題を解くために使用され、ここでは利益を最大化するために利益係数を負の値に変換しています。制約は労働力と機械時間に関するもので、これらの制約を満たしつつ利益を最大化する製品AとBの生産量が求められます。
以下、実行結果です。
最適解: [100. 0.] 最大利益: 5000.0
実行結果は、製品AとBの最適な生産量とその時の最大利益を示します。この結果をもとに、アルファ社はリソースを最も効率的に利用し、利益を最大化する生産計画を立てることができます。
事例２：輸送と物流問題
ベータデリバリー社は物流業界で活動する企業で、顧客に製品を効率的かつ迅速に配送するための最適なルートを常に探しています。
同社は複数の配送センターから複数の目的地に製品を配送する必要があり、各ルートには異なるコストと時間がかかります。最適なルートを選択することで、配送コストを削減し、顧客満足度を向上させたいと考えています。
- 配送センター: 3箇所（A, B, C）
- 目的地: 3箇所（X, Y, Z）
- 配送センターから目的地までのコスト（ドル/単位）:
X Y Z A 4 5 6 B 6 4 3 C 5 4 2 - x_{ij}: 出発地 i から目的地 j への輸送量
- i 1:A, 2:B, 3:C
- j 1:X, 2:Y, 3:Z
定式化（ベクトルと行列で表現）すると以下のようになります。
目的関数：
\displaystyle \text{minimize } \begin{bmatrix}1 & 1 & 1\end{bmatrix}\begin{bmatrix} 4 & 5 & 6 \\ 6 & 4 & 3 \\ 5 & 4 & 2 \end{bmatrix} \begin{bmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{bmatrix}^T \begin{bmatrix}1 \\ 1 \\ 1 \end{bmatrix}
制約条件：
\displaystyle \begin{array}{rrrrr} \begin{bmatrix}1 & 1 & 1\end{bmatrix} \begin{bmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{bmatrix} = \begin{bmatrix}40 & 70 & 50 \end{bmatrix} \\ \\ \displaystyle \begin{bmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{bmatrix} \begin{bmatrix}1 \\ 1 \\ 1\end{bmatrix} \le \begin{bmatrix}50 \\ 60 \\ 50 \end{bmatrix} \\ \\ \displaystyle x_{ij} \ge 0 \end{array}
- x_1：製品Aの生産量
- x_2：製品Bの生産量
この問題をコードにすると、以下のようになります。
import numpy as np
import scipy.optimize as opt
# Convert the list to a numpy array
costs = np.array([
[4, 5, 6],
[6, 4, 3],
[5, 4, 2]
])
# 供給量
supply = [50, 60, 50]
# 需要量
demand = [40, 70, 50]
result = opt.linprog(
c=costs.flatten(),
A_eq=[
# 供給制約
[1 if i//3 == j else 0 for i in range(9)] for j in range(3)
] + [
# 需要制約
[1 if i%3 == j else 0 for i in range(9)] for j in range(3)
],
b_eq=supply + demand,
bounds=(0, None)
)
if result.success:
print("最適解:", result.x.reshape(3, 3))
print("最小コスト:", result.fun)
else:
print("最適化問題の解決に失敗しました。")
このコードは、与えられた配送センターから目的地までのコストに基づき、配送コストを最小限に抑えるための最適な配送ルートを計算します。linprog関数は線形最適化問題を解くために使用され、ここではコストを最小化するための配送ルートを見つけることを目指しています。供給量と需要量に基づいた制約が設定され、これらの制約を満たしつつ配送コストを最小化するルートが求められます。
以下、実行結果です。
最適解: [[40. 10. 0.] [ 0. 60. -0.] [ 0. 0. 50.]] 最小コスト: 550.0
各配送センターから各目的地への最適な配送量とその時の最小コストを示します。この結果をもとに、ベータデリバリー社はコストを最小限に抑えつつ顧客への製品配送を最適化することができます。
事例３：ポートフォリオの最適化
ガンマインベスト社は投資運用会社であり、顧客に代わって資産を運用しています。
彼ら・彼女らの主な課題は、リスクを管理しつつ、リターンを最大化するバランスの取れた投資ポートフォリオを構築することです。線形最適化を利用して、リスク許容度に応じた最適な資産配分を決定し、顧客の期待リターンを達成することが目標です。
- 投資可能な資産クラス: 株式、債券、コモディティ、現金
- 各資産の予想リターン率(%): 株式: 8, 債券: 3, コモディティ: 5, 現金: 1
- 各資産のリスク評価(0〜1): 株式: 0.7, 債券: 0.3, コモディティ: 0.5, 現金: 0.1
- 顧客の期待リターン率(%): 5
- 顧客のリスク許容度(0〜1): 0.4
- 投資額合計: 100万ドル
定式化（ベクトルと行列で表現）すると以下のようになります。
目的関数：
\displaystyle \text{minimize } -1 \times \begin{bmatrix}0.08 & 0.03 & 0.05 & 0.01 \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix}
制約条件：
\displaystyle \begin{array}{rrrrr} \displaystyle \begin{bmatrix}1 & 1 & 1 & 1 \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix}=1 \\ \\ \displaystyle \begin{bmatrix}0.7 & 0.3 & 0.5 & 0.1 \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} \le 0.4 \\ \\ \displaystyle x_{i} \ge 0 \end{array}
- x_i：投資先 i への投資比率
この問題をコードにすると、以下のようになります。
import scipy.optimize as opt
# 資産クラスごとの予想リターン率とリスク
returns = [0.08, 0.03, 0.05, 0.01]
risks = [0.7, 0.3, 0.5, 0.1]
# 顧客の期待リターンとリスク許容度
target_return = 0.05
risk_tolerance = 0.4
# 最適化問題の解決
result = opt.linprog(
c=[-r for r in returns], # リターン最大化（負の符号で最小化問題に変換）
A_eq=[[1, 1, 1, 1]], # 投資額の合計が1に等しい
b_eq=[1],
A_ub=[risks], # リスク許容度に基づく制約
b_ub=[risk_tolerance],
bounds=[(0, 1) for _ in returns] # 投資比率は0〜1の間
)
if result.success:
print("最適な投資比率:", result.x)
print("予想リターン率:", sum(r * x for r, x in zip(returns, result.x)))
else:
print("最適化問題の解決に失敗しました。")
このコードは、与えられたリスク許容度と目標リターンを満たすように資産を配分することを目指します。linprog関数は線形最適化問題を解くために使用され、ここではリターンを最大化しつつリスクを制限内に抑えるための最適な投資比率を求めています。結果は、顧客のリスク許容度と目標リターンに基づいて各資産クラスにどれだけ投資すべきかを示します。
以下、実行結果です。
最適な投資比率: [0.5 0. 0. 0.5] 予想リターン率: 0.045000000000000005
最適な投資比率とその投資比率に基づく予想リターン率を示しています。この結果により、ガンマインベスト社は顧客の期待に応えるポートフォリオを構築し、リスク管理を行うことができます。
まとめ
今回の「線形最適化の基礎」では、線形最適化に関する重要な概念とその実践的な適用方法を学びました。線形最適化の基本理論から始め、目的関数と制約の設定、そしてPythonのScyPyライブラリを用いた具体的な解法まで、幅広いトピックをカバーしました。また、実業務での応用事例を通じて、理論と実践のつながりを理解しました。
- 基本理論: 線形最適化は、目的関数と一連の線形制約条件の下で最適な解を見つける数学的手法です。
- 目的関数と制約の設定: 正確な目的関数の設定と実現可能な制約条件の定義が成功の鍵です。
- 実践的応用: 線形最適化は、リソースの割り当て、輸送と物流、ポートフォリオ管理など多岐にわたる分野で応用されています。
- ScyPyを使った解法: PythonのScyPyライブラリを使用して、様々な線形最適化問題を解くことができます。
次回の「非線形最適化の基礎」では、線形最適化の枠を超えた、より複雑な問題に取り組みます。
非線形最適化は、目的関数や制約が非線形の場合に適用される手法です。非線形最適化の基本的な理論から、制約の有無による解法の違い、そしてScyPyを用いた具体的な問題の解法まで、幅広い知識を提供します。また、実際のビジネスや工学の問題を例に、非線形最適化の応用を解説します。
次回も、最適化手法の理解を深め、実践的なスキルを磨くための貴重な情報を提供することを目指します。非線形最適化の世界への一歩を踏み出しましょう！
