データ分析の世界では、完璧なデータセットに出会うことは稀です。
データの欠損は避けられない現実であり、これをどのように扱うかが分析の成果を左右します。
今回は、欠損データを効果的に扱うための様々なアプローチを紹介します。
平均値から多変量補完まで、各手法の特徴、適用条件、そしてその利点と落とし穴を解説します。
Contents [hide]
欠損値の補完の重要性

データセット内の欠損データは、多くの分析プロジェクトにとって大きな課題です。
欠損データを適切に扱うことは、分析の正確性を保証し、より信頼性の高い洞察を得るために不可欠です。欠損データの補完には、データの特性を考慮し、適切な手法を選択する必要があります。
例えば、ある企業の従業員データセットがあるとしましょう。
| 従業員ID | 年齢 | 経験年数 | 年収 |
|---|---|---|---|
| 0 | 22 | 25 | 6,107,661 |
| 1 | 25 | 25 | 9,264,904 |
| 2 | 25 | 13 | 8,118,729 |
| 3 | 61 | 2 | 5,951,283 |
| 4 | 31 | 39 | 7,527,056 |
| 5 | 41 | 24 | 5,527,987 |
| 6 | 43 | 25 | NaN |
| 7 | 58 | 18 | NaN |
| 8 | 45 | 38 | 6,743,151 |
| 9 | 28 | 26 | NaN |
このデータセットには年齢、経験年数、年収などの情報が含まれていますが、一部の従業員の年収データが欠損(NaN)しているとします。この欠損データを無視すると、平均年収の計算などに影響を及ぼし、誤ったビジネス上の判断を引き起こす可能性があります。
欠損データを補完することで、より正確な統計分析を行い、企業の人事戦略や報酬体系の決定に役立つ情報を提供できます。この章では、データの特性と欠損のパターンを理解することの重要性に焦点を当てます。
どのような処理を行うべきか?
処理フローチャート
以下のフローチャートは、欠損値があるデータセットに対してどのような処理を行うべきかを判断するためのものです。
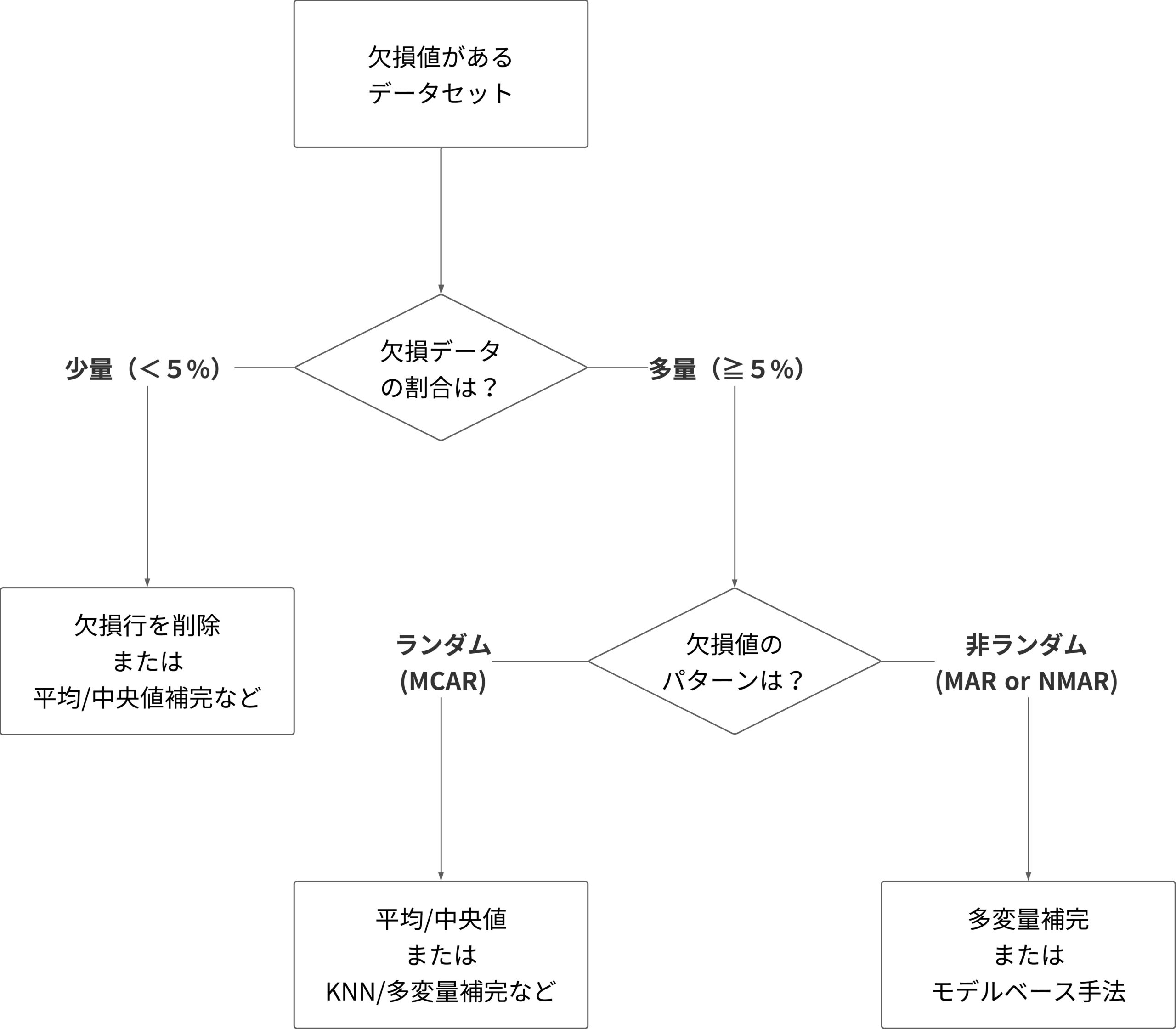
このフローチャートは、欠損データの割合や欠損のパターンに基づいて、行を削除する、変数を削除する、平均値や中央値で補完するなどの選択肢を提供します。
- データセットに欠損値がある場合、まず欠損データの割合を確認します。
- もし欠損データが全体の5%未満であれば、欠損行を削除するか、平均値または中央値、ランダムサンプリング、任意の値による補完を検討します。
- 欠損データが5%以上の場合、欠損がランダムか非ランダムかを確認します。
- ランダムな欠損(MCAR)の場合、平均値または中央値、ランダムサンプリング、任意の値による補完や、KNN(K近傍法)や多変量補完などを検討します。
- 非ランダムな欠損(MARやNMAR)の場合、多変量補完やモデルベース(機械学習など)の手法を検討します。
欠損データパターン
MCAR (Missing Completely at Random)
MCARは、欠損が完全にランダムである状況を指します。つまり、データが欠損している理由が観測されたデータ(そのデータセット内の他の変数)や欠損しているデータ自体とは無関係です。
例: サーベイの回答者がページを見落として質問に答えなかった場合。
MCARの場合、欠損データを除外してもデータ分析においてバイアスが生じることは少ないです。
MAR (Missing at Random)
MARは、欠損がランダムであるが、それが他の観測されたデータによって説明可能である状況を指します。
例: 若年層は健康関連の質問に答える可能性が低いが、これは年齢という観測データによって説明可能である場合。
MARでは、他の変数を使って欠損データのパターンをモデル化し、その影響を緩和することができます。
NMAR (Not Missing at Random)
NMARは、欠損が観測されていないデータ自体に依存している状況を指します。
例: ある疾患を持つ患者が健康状態に関する質問に答えることを避ける場合。
NMARの場合、欠損データは分析にバイアスをもたらす可能性が高く、これを考慮するために特別な統計的手法が必要です。
欠損値を示す指標を追加し分析
データ分析において、欠損値の存在自体を示す追加の指標(フラグ)を作成することで、欠損データの割合やそのパターンを分析することができます。
- 欠損データの割合は?
- 欠損データのパターンは?
例えば、金融機関のローン申請データセットを考えましょう。
申請者の職歴や年収などの情報が含まれていますが、一部の申請者が特定の情報を提供していない場合があります。ここで、各欠損データポイントに対して、欠損を示すフラグ(例えば、0と1)を割り当てることができます。
| 申請者ID | 職歴年数 | 年収 | 年収情報欠損フラグ |
|---|---|---|---|
| 1 | 12 | 7,853,461 | 0 |
| 2 | 15 | 8,739,698 | 0 |
| 3 | 21 | NaN | 1 |
| 4 | 0 | NaN | 1 |
| 5 | 3 | NaN | 1 |
| 6 | 27 | NaN | 1 |
| 7 | 3 | 5,316,312 | 0 |
| 8 | 7 | 7,033,356 | 0 |
| 9 | 9 | 4,701,626 | 0 |
| 10 | 19 | 6,735,681 | 0 |
例えば、年収情報が欠損している申請者に対して「年収情報欠損フラグ」を設定し、このフラグを分析に組み込みます。
この方法により、欠損データのパターンや、それが最終的なローン承認決定にどのように影響するかをより詳細に分析することが可能になります。
欠損データの削除
欠損データの削除は、補完手法の代わりに、欠損値を含むデータポイントをデータセットから完全に除去するアプローチです。この方法は、欠損が少量で、その除去がデータセット全体の品質に大きな影響を与えない場合に適しています。
例えば、小売店の顧客満足度調査データを考えます。
このデータセットには、顧客の意見や評価が含まれていますが、一部の回答が欠損しています。欠損データが全体の少ない割合であれば、これらを削除しても統計的な分析に大きな影響はないかもしれません。
| 顧客ID | 商品の品質評価 | サービスの評価 | 総合満足度 |
|---|---|---|---|
| 1 | 1 | 2 | 3.0 |
| 2 | NaN | 3 | NaN |
| 3 | 2 | NaN | NaN |
| 4 | 1 | 4 | 3.0 |
| 5 | 4 | 3 | 1.0 |
| 6 | 4 | 1 | NaN |
| 7 | 4 | 1 | 2.0 |
| 8 | 4 | 1 | 2.0 |
| 9 | NaN | 3 | NaN |
| 10 | 4 | NaN | 1.0 |
欠損データの削除は、データの量が十分に多く、欠損が分析結果に大きなバイアスを与えない場合に適用可能です。しかし、欠損が多い場合や欠損が特定のパターンを持つ場合、データを単純に削除することは適切ではなく、分析の質を低下させる可能性があります。
平均値/中央値による補完
欠損データの補完方法の中で最も基本的かつ広く使われるのが、平均値や中央値を用いる手法です。この方法は、データの分布が正規分布に近い場合や外れ値の影響を受けにくい場合に特に有効です。
例えば、ある企業の従業員データセットがあるとしましょう。このデータセットには年齢、経験年数、年収などの情報が含まれていますが、一部の従業員の年収データが欠損しているとします。
| 従業員ID | 年齢 | 経験年数 | 年収 |
|---|---|---|---|
| 0 | 22 | 25 | 6,107,661 |
| 1 | 25 | 25 | 9,264,904 |
| 2 | 25 | 13 | 8,118,729 |
| 3 | 61 | 2 | 5,951,283 |
| 4 | 31 | 39 | 7,527,056 |
| 5 | 41 | 24 | 5,527,987 |
| 6 | 43 | 25 | NaN |
| 7 | 58 | 18 | NaN |
| 8 | 45 | 38 | 6,743,151 |
| 9 | 28 | 26 | NaN |
欠損している年収データを補完する場合、全従業員の年収の平均値または中央値を用いることができます。
- 平均値補完: 例えば、全従業員の年収平均が500万円であれば、欠損しているデータポイントには全員500万円を割り当てます。
- 中央値補完: 年収のデータが大きく偏っている場合(例えば、非常に高い年収をもつ役員がいるなど)、中央値を使用すると、外れ値の影響を受けにくくなります。
この方法は、欠損データがランダムに分布している場合(MCAR: Missing Completely at Random)に最適で、簡単に実装できる利点があります。しかし、元のデータの分布を変える可能性があるため、分析の目的に応じて慎重に選択する必要があります。
ランダムサンプリングによる補完
ランダムサンプリングによる補完は、既存のデータポイントからランダムに値を抽出して欠損値を埋める方法です。このアプローチは、データの全体的な分布を維持しつつ欠損データを補完するのに有効です。
小売業の顧客購買データを考えましょう。このデータセットには、顧客が購入した商品のカテゴリが含まれていますが、一部の記録で商品カテゴリが欠損している場合があります。このような場合、既存の記録からランダムにカテゴリを選んで補完します。
既存の商品カテゴリからランダムに選ばれたカテゴリを欠損データに割り当てます。
この方法は、データの自然な変動を保ちつつ欠損値を埋めるのに役立ちますが、欠損の原因やパターンについての洞察を提供するものではありません。
任意の値による補完

基本的な考え方
任意の値による補完は、特定の値を選択して欠損データを置き換える手法です。この方法は、欠損が特定の意味を持つ場合やデータに特別なパターンがある場合に有効です。
例として、製造業の機械のメンテナンス記録を考えましょう。
このデータセットには、各機械の最終メンテナンス日が含まれていますが、一部の機械のデータが欠損しているとします。この場合、欠損値を「メンテナンス未実施」と解釈し、特定の日付(例えば、データ収集日の1年前)で補完することが考えられます。
欠損データに「2022年1月1日」という特定の日付を割り当てることで、メンテナンスが長期間行われていない機械を識別できます。
この手法は、データの特性や分析の目的を理解している場合に特に有効です。ただし、選択した値がデータの他の側面に影響を与える可能性があるため、注意が必要です。
分布の端値による補完
補完する値を、分布の端値で実施することがあります。
この分布の端値による補完は、データセットの分布を考慮して、最小値や最大値などの極端な値を欠損値の代わりに使用する手法です。これは、欠損がデータの特定の極端な状態を示唆している場合に適しています。
金融機関の顧客クレジットスコアデータを例にとります。
このデータセットには、顧客のクレジットスコアが記録されていますが、一部の顧客のスコアが欠損しているとします。欠損がクレジット履歴の欠如を意味する場合、これらの顧客に最低スコアを割り当てることができます。
クレジットスコアの可能な最低値(例えば、300)を欠損データに割り当てます。
この方法は、欠損が特定の状況を示している場合に有用ですが、データの全体的な分布を歪める可能性があるため、分析の目的に応じて慎重に選択する必要があります。
頻出カテゴリによる補完
カテゴリカルデータの場合、頻出カテゴリによる補完を実施します。
データセット内で最も頻繁に出現するカテゴリを使用することです。これは、欠損値がランダムであると仮定した場合に有効な戦略となります。
顧客のデモグラフィック情報を含む小売業のデータセットを考えます。
このデータセットには、顧客の好みの商品カテゴリが記録されていますが、一部の顧客のデータが欠損しています。この場合、最も一般的な商品カテゴリを欠損値の代わりに使用できます。
データセットにおいて最も頻繁に購入されている商品カテゴリ(例えば、「食料品」)を欠損データに割り当てます。
この手法は、カテゴリデータの欠損値を補完する際の簡単な方法ですが、元のデータの分布を変える可能性があるため、適用する際は慎重に検討する必要があります。
欠損値をカテゴリとして処理
他には、欠損値を別のカテゴリとして扱うアプローチがあります。
欠損値を単なる「欠損」ではなく、データ内で独自のカテゴリとして扱う方法もあります。これは、欠損自体が重要な情報を持つ場合や、欠損の理由が分析に影響を与える可能性がある場合に適しています。
健康調査のデータセットを例にとります。
このデータセットでは、被調査者の運動習慣、食生活、健康状態などが記録されていますが、特定の質問に対する回答が欠損している場合があります。ここで、欠損値を「回答拒否」または「情報不明」といった別のカテゴリとして扱います。
回答が欠損している項目に「回答拒否」や「情報不明」といったラベルを割り当て、それを分析に組み込みます。
この方法は、欠損そのものが意味を持つ場合に非常に有効ですが、欠損の理由が不明確な場合は、誤解を招く可能性があります。
多変量補完やモデルベース(機械学習など)

基本的な考え方
多変量補完は、他の変数の情報を利用して欠損データを補完する手法です。この方法は、欠損値が他の変数と相関している場合に特に有効です。多変量補完には、機械学習アルゴリズムを用いることも一般的です。
| 手法 | 特徴 | 適用条件 |
|---|---|---|
| 多重代入法 | 複数の補完されたデータセットを生成し、結果を統合 | 欠損がランダムで、データセットが大きい場合 |
| K近傍法 | 近傍データポイントの平均や中央値で欠損値を補完 | 小規模なデータセット、類似データが存在する場合 |
| 決定木法 | 他の変数を用いて欠損値を持つ変数を予測 | 関連する変数が明確な場合 |
| ランダムフォレスト | 複数の決定木を用いて欠損値を予測 | 複雑なデータ構造、ランダムフォレストの仮定に適合する場合 |
| 回帰代入法 | 他の変数を独立変数として欠損値を持つ変数の回帰分析 | 線形関係が存在する場合 |
| Expectation-Maximizationアルゴリズム | 欠損データの最尤推定値を求める反復アルゴリズム | 共分散構造が重要な場合 |
| ニューラルネットワーク | ディープラーニングを用いた複雑な関係の捉え方 | 非線形関係や大量のデータ |
| オートエンコーダー | データの圧縮表現と再構築を学習 | データの潜在的特徴を捉える必要がある場合 |
| GANを使用した補完 | リアルなデータを生成し欠損値を補完 | 複雑なデータ構造、リアルなデータ生成が必要な場合 |
| ベイジアンネットワーク | データ間の確率的関係をモデリング | 確率的関係のモデリングが重要な場合 |
健康保険会社の顧客データを例に取ります。このデータセットには年齢、性別、医療費、生活習慣などの情報が含まれていますが、一部の顧客の医療費データが欠損しています。他の変数(年齢、性別、生活習慣)の情報を利用して、医療費の欠損値を推定します。
欠損している医療費データに対して、他の変数との関係をモデル化し、そのモデルを使用して欠損値を予測します。
多変量補完は、データ間の複雑な関係を考慮に入れることができるため、より精度の高い補完が可能になります。しかし、適切なモデルの選択とパラメータの調整が重要です。
古典的な手法
多重代入法(Multiple Imputation)
欠損値を複数回にわたって推測し、複数の補完されたデータセットを生成する手法です。最終的な分析結果は、これらの異なるデータセットの結果を統合することで得られます。
K近傍法(K-Nearest Neighbors, KNN)
欠損値を持つデータポイントと最も類似しているK個の近傍データポイントを見つけ、これらのデータの平均値や中央値などで欠損値を補完します。
決定木法(Decision Trees)
欠損値を持つ変数を予測するために、他の変数を使用して決定木を構築します。この木の予測値を欠損値の補完に使用します。
ランダムフォレスト(Random Forest)
決定木法を拡張し、複数の決定木を用いて欠損値の予測を行います。各木の予測結果の平均を取ることで、より堅牢な推定値を得ることができます。
回帰代入法(Regression Imputation)
欠損値を持つ変数に対して、他の変数を独立変数として回帰分析を行い、その予測値を欠損値の補完に用います。
Expectation-Maximization(EM)アルゴリズム
欠損データを持つ変数間の共分散構造を利用し、欠損値の最尤推定値を求める反復アルゴリズムです。
これらの手法は、データセットの特性や分析の目的に応じて選択され、適切に実装される必要があります。また、複数の手法を組み合わせることで、より精度の高い補完を行うことも可能です。
最近の手法
ニューラルネットワークを用いた補完(Neural Network Imputation)
欠損データを含むデータセットに対して、ディープニューラルネットワーク(DNN)や畳み込みニューラルネットワーク(CNN)などを使用して、欠損値を予測します。これらのモデルは非線形関係や複雑なパターンを捉えることができます。
オートエンコーダー(Autoencoders)
入力データの圧縮表現(エンコード)とその再構築(デコード)を学習します。欠損値がある場合に、データの再構築を通じて補完を行うことができます。
Generative Adversarial Networks(GAN)を使用した補完
生成モデルと識別モデルが互いに競合しながら学習するフレームワークです。欠損データを持つデータセットに対して、GANを用いてリアルなデータを生成し、欠損値を補完します。
ベイジアンネットワークを用いた補完
データ間の確率的関係をモデリングするために、ベイジアンネットワークを使用します。これにより、欠損値の確率的推定が可能になります。
これらの高度な手法は、特に大量のデータや複雑なデータ関係が存在する場合に有効ですが、モデルの設計やパラメータの調整が重要です。また、計算コストやモデルの解釈可能性も考慮する必要があります。
今回のまとめ
今回は、「欠損データの克服: 分析の精度を高めるスマートな戦略」というお話ししました。
データ分析の道のりは、しばしば欠損データという障害に直面します。重要なのは、欠損データがランダムか非ランダムかを理解し、それに適した処理方法を選択することです。平均値や中央値による補完から多変量補完、さらにはモデルベースのアプローチまで、各方法は特定の状況において最適です。
欠損データの扱い方は、データの種類、欠損の量、分析の目的によって異なります。最も重要なことは、欠損データを適切に処理することで、分析の信頼性を高め、より正確な洞察を得ることができるということです。
欠損データの問題に直面したとき、この記事があなたの分析を成功へと導く一助となることを願っています。

