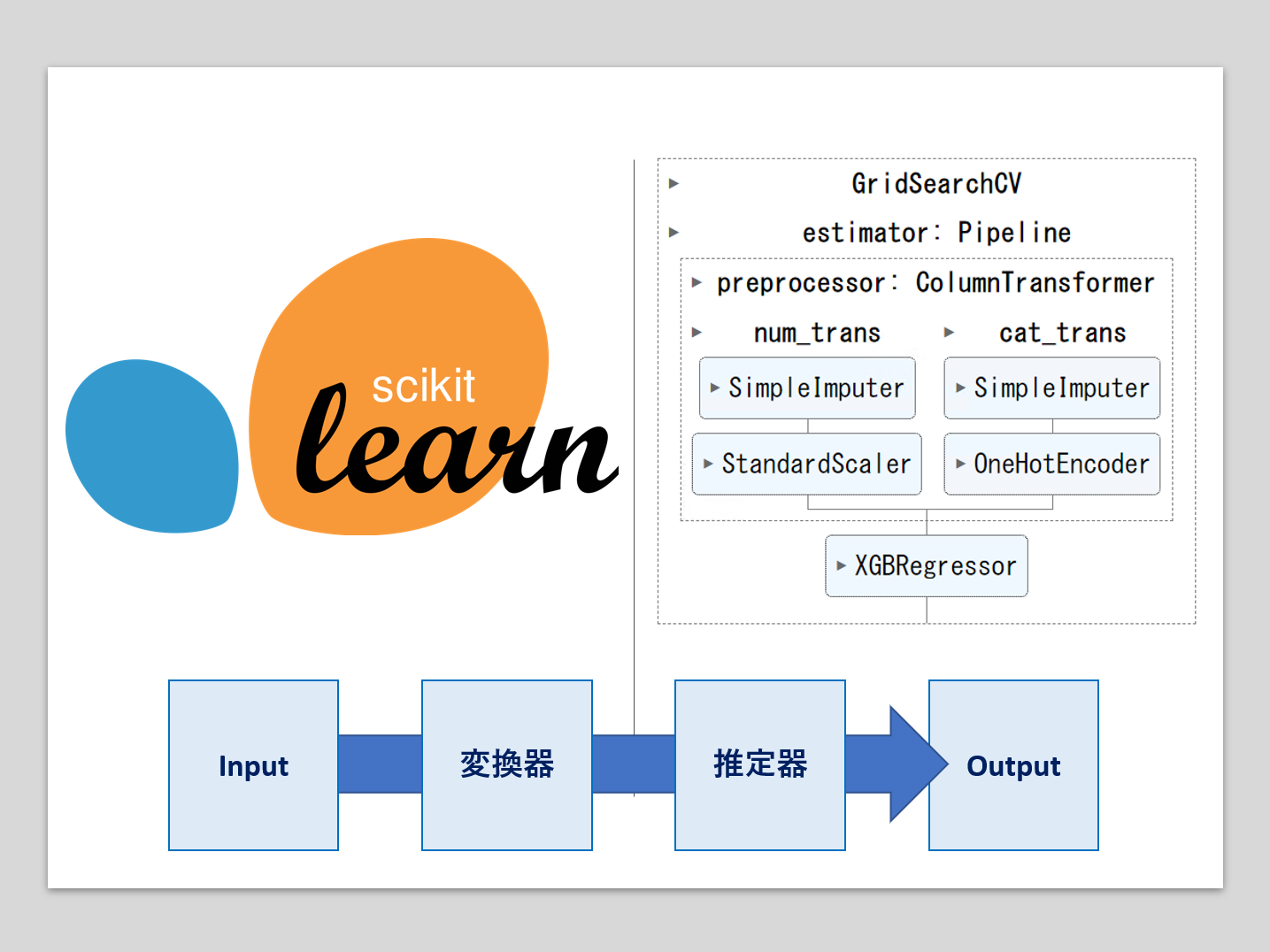
機械学習のパイプラインとは、複数の処理を直列に連結したものです。

最小構成は、1つの変換器と1つの推定器（予測器）を連結したものです。

• 変換器：特徴量X（説明変数）などの欠測値処理や変数変換などの、特徴量変換（Transformor）
• 推定器：線形回帰モデルやXGBoostなどの数理モデルを使い、目的変数yの予測を実施（Estimator）

多くの場合、Inputは特徴量（説明変数）Xで、Outputは目的変数yの予測値です。

全ての変数に対し同じ変換を施すこともあるでしょうが、いつも全ての変数に対し同じ変換を施すわけでもありません。

前回は、変数ごとに利用する関数を自動選択し、さらにその関数ごとにハイパーパラメータをチューニングする方法について説明しました。

scikit-learnの機械学習パイプライン入門（その6：変数ごとに関数選択＋チューニング自動化）

今回は、さらに推定器も自動選択し、選択した推定器のハイパーパラメータもチューニングする方法についてお話しします。

ここまでくると、ちょっとした簡易AutoML（自動機械学習）ですね。

利用する関数（変数変換用の関数）

今回は、前回と同様に以下の3つのS字曲線の関数を利用します。

• 一般化ロジスティック関数
• 一般化ハイパボリックタンジェント関数
• ゴンペルツ関数

それぞれ、ハイパーパラメータが存在します。

詳細は、前回の記事を参照してください。

 

利用する推定器

今回は、以下の3つのツリー系の推定器を利用します。

• Decision Tree：scikit-learn（sklearn）のDecisionTreeRegressorを使います。
• Random Forest：scikit-learn（sklearn）のRandomForestRegressorを使います。
• XGBoost：xgboostのXGBRegressorを使います。

それぞれ、ハイパーパラメータが存在します。

回帰問題を取り扱うので、すべてRegressorになります。

 

　Decision Tree Regressor

決定木は、データを複数のシンプルな決定ルールに基づいて分割することで予測を行います。

過学習に注意する必要があり、特にデータが少ない場合や変数が多い場合に注意が必要です。

決定木は解釈が容易で、どのように予測が行われたかを理解しやすいです。

 

以下、コード例になります。

from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np

# サンプルデータ（Xは特徴量、yは目的変数）
X, y = np.random.rand(100, 4), np.random.rand(100)

# データを訓練セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# モデルのインスタンス化と訓練
regressor = DecisionTreeRegressor()
regressor.fit(X_train, y_train)

# テストデータに対する予測と評価
y_pred = regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")

 

このコードは、scikit-learnライブラリを使用して決定木回帰モデルを作成し、評価するためのものです。

それぞれのステップを簡単に説明します。

• ライブラリのインポート
  • DecisionTreeRegressor: scikit-learnから決定木回帰モデルのクラス。
  • train_test_split: データセットを学習セットとテストセットに分割する関数。
  • mean_squared_error: 予測値の精度を評価するための平均二乗誤差を計算する関数。
  • numpy: 数値計算を行うためのライブラリ。
• サンプルデータの生成
  • X: 0から1の間のランダムな数値を含む100行4列の配列（特徴量）。
  • y: 0から1の間のランダムな数値を含む100要素の配列（目的変数）。
• データの分割
  • train_test_splitを使用して、データセットを学習セット（80%）とテストセット（20%）に分割。
• モデルのインスタンス化と学習
  • DecisionTreeRegressorのインスタンスを作成。
  • fitメソッドを使って、学習セットに基づいてモデルを学習。
• テストデータに対する予測と評価
  • predictメソッドを使用してテストセットの目的変数を予測。
  • mean_squared_errorを使って、実際の目的変数と予測値の間の平均二乗誤差を計算。
  • 計算されたMSE（平均二乗誤差）を出力。

 

以下、実行結果です。

Mean Squared Error: 0.16076065682713933

 

　Random Forest Regressor

ランダムフォレストは、複数の決定木を組み合わせて予測精度を高めるアンサンブル学習の一種です。

各決定木はデータセットのランダムなサブセットで訓練され、最終的な予測は各木の予測の平均または多数決によって行われます。

過学習に対して比較的ロバストで、多くの実問題に対して良好なパフォーマンスを示します。

 

以下、コード例になります。

from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np

# サンプルデータ（Xは特徴量、yは目的変数）
X, y = np.random.rand(100, 4), np.random.rand(100)

# データを学習セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# モデルのインスタンス化と学習
rf_regressor = RandomForestRegressor(n_estimators=100)
rf_regressor.fit(X_train, y_train)

# テストデータに対する予測と評価
y_pred = rf_regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")

 

このコードは、scikit-learnライブラリを使用してランダムフォレスト回帰モデルを作成し、評価するためのものです。

• ライブラリのインポート
  • RandomForestRegressor: scikit-learnからランダムフォレスト回帰モデルのクラス。
  • train_test_split: データセットを学習セットとテストセットに分割する関数。
  • mean_squared_error: 予測値の精度を評価するための平均二乗誤差を計算する関数。
  • numpy: 数値計算を行うためのライブラリ。
• サンプルデータの生成
  • X: 0から1の間のランダムな数値を含む100行4列の配列（特徴量）。
  • y: 0から1の間のランダムな数値を含む100要素の配列（目的変数）。
• データの分割
  • train_test_splitを使用して、データセットを学習セット（80%）とテストセット（20%）に分割。
• モデルのインスタンス化と学習
  • RandomForestRegressorのインスタンスを作成。n_estimators=100は、100個の決定木を使用することを意味します。
  • fitメソッドを使って、学習セットに基づいてモデルを学習。
• テストデータに対する予測と評価
  • predictメソッドを使用してテストセットの目的変数を予測。
  • mean_squared_errorを使って、実際の目的変数と予測値の間の平均二乗誤差を計算。
  • 計算されたMSE（平均二乗誤差）を出力。

 

以下、実行結果です。

Mean Squared Error: 0.13680114196139376

 

　XGBoost Regressor

XGBoostは、勾配ブースティングと呼ばれるアンサンブル学習の一種で、連続する各決定木が前の木の誤差を修正するように訓練されます。

高い予測精度を持ち、多くの機械学習コンペティションで広く使用されています。

パラメータチューニングが重要で、適切なパラメータ設定によって性能が大きく変わることがあります。

 

以下、コード例になります。

from xgboost import XGBRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np

# サンプルデータ（Xは特徴量、yは目的変数）
X, y = np.random.rand(100, 4), np.random.rand(100)

# データを学習セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# モデルのインスタンス化と学習
xgb_regressor = XGBRegressor(n_estimators=100, learning_rate=0.1)
xgb_regressor.fit(X_train, y_train)

# テストデータに対する予測と評価
y_pred = xgb_regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")

 

このコードは、XGBoost（eXtreme Gradient Boosting）ライブラリを使用してXGBRegressorモデルを作成し、評価するためのものです。

• ライブラリのインポート
  • XGBRegressor: XGBoostライブラリからの勾配ブースティング回帰モデルのクラス。
  • train_test_split: データセットを学習セットとテストセットに分割する関数。
  • mean_squared_error: 予測値の精度を評価するための平均二乗誤差を計算する関数。
  • numpy: 数値計算を行うためのライブラリ。
• サンプルデータの生成
  • X: 0から1の間のランダムな数値を含む100行4列の配列（特徴量）。
  • y: 0から1の間のランダムな数値を含む100要素の配列（目的変数）。
• データの分割
  • train_test_splitを使用して、データセットを学習セット（80%）とテストセット（20%）に分割。
• モデルのインスタンス化と学習
  • XGBRegressorのインスタンスを作成。n_estimators=100は、100個のブースティングステージ（決定木）を使用することを意味し、learning_rate=0.1は学習率を設定します。
  • fitメソッドを使って、学習セットに基づいてモデルを学習。
• テストデータに対する予測と評価
  • predictメソッドを使用してテストセットの目的変数を予測。
  • mean_squared_errorを使って、実際の目的変数と予測値の間の平均二乗誤差を計算。
  • 計算されたMSE（平均二乗誤差）を出力。

 

以下、実行結果です。

Mean Squared Error: 0.13186952043331815

 

パイプラインの学習と予測

サンプルデータは前回と同じ、特徴量（説明変数）は5変数で、目的変数yが1つのデータセットです。

以下からダウンロードできます。

sample_data.csv
https://www.salesanalytics.co.jp/913d

 

　準備

まず、必要なモジュールを読み込みます。

以下、コードです。

import pandas as pd
import numpy as np
import xgboost as xgb
import optuna

from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import (
    mean_absolute_error, 
    mean_absolute_percentage_error,
    r2_score)

import matplotlib.pyplot as plt

 

• pandas: データ分析と操作のための強力なライブラリです。主にデータフレームとシリーズというデータ構造を用いて、データの読み込み、加工、分析を行います。
• numpy: 数値計算を効率的に行うためのライブラリです。配列（アレイ）を中心としたデータ構造を提供し、高速なベクトル演算や数学的処理が可能です。
• xgboost: 勾配ブースティングアルゴリズムを実装したライブラリです。分類や回帰などの機械学習タスクにおいて高いパフォーマンスを発揮し、特に競技プログラミングや実務のデータサイエンス分野で広く使われています。
• optuna: ハイパーパラメータチューニングを自動化するためのライブラリです。機械学習モデルのパフォーマンス向上のために、最適なハイパーパラメータの組み合わせを探索するのに役立ちます。
• RandomForestRegressor: ランダムフォレストというアンサンブル学習の手法を実装したもので、特に回帰タスク（連続値の予測）に使用されます。
• DecisionTreeRegressor: 決定木を用いた回帰モデルです。データを分割し、それぞれの分割が目的変数の予測に役立つように木構造を形成します。
• BaseEstimator, TransformerMixin: これらはカスタムトランスフォーマーや推定器を作成する際に使用されるクラスです。BaseEstimatorとTransformerMixinを継承することで、独自のデータ変換や前処理手順を組み込むことができます。
• Pipeline: 複数のデータ変換ステップを連結し、単一の処理フローとして扱うためのユーティリティです。データの前処理とモデルの訓練を一連のステップとしてまとめるのに便利です。
• train_test_split: データセットを訓練用データセットとテスト用データセットに分割するための関数です。モデルの汎化能力を評価するために使われます。
• mean_absolute_error, mean_absolute_percentage_error, r2_score: これらはモデルのパフォーマンスを評価するためのメトリクスです。平均絶対誤差(MAE)、平均絶対パーセンテージ誤差(MAPE)、決定係数(R²)を計算します。
• matplotlib.pyplot: グラフやチャートを描画するためのライブラリです。データの可視化や分析結果の表現に用いられます。

 

次に、サンプルデータを読み込み、学習データとテストデータに分割します。

以下、コードです。

# データの読み込みと分割
data = pd.read_csv('sample_data.csv')
X = data.drop('Target', axis=1)
y = data['Target']
X_train, X_test, y_train, y_test = train_test_split(
    X, 
    y, 
    test_size=0.2, 
    random_state=42)

 

このコードは、CSVファイルからデータを読み込み、特徴量と目標変数に分割した後、データセットを学習データとテストデータに分割するプロセスを行っています。

• データの読み込み:
  • data = pd.read_csv('sample_data.csv'): これはpandasライブラリのread_csv関数を使って、’sample_data.csv’というCSVファイルからデータを読み込む命令です。読み込まれたデータはpandasデータフレームdataに格納されます。
• 特徴量と目標変数の定義:
  • X = data.drop('Target', axis=1): ここで、データフレームdataから’Target’という名前の列を除外し、残りの列を新しいデータフレームXに格納しています。これらの列は機械学習モデルの特徴量として使用されます。
  • y = data['Target']: ‘Target’列はdataデータフレームから直接取り出され、目標変数（予測したい値）としてyに割り当てられます。
• データの分割:
  • X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42): この行はtrain_test_split関数を使って、特徴量（X）と目標変数（y）を学習データ（X_train, y_train）とテストデータ（X_test, y_test）に分割しています。test_size=0.2はデータセットの20%をテストデータとして使用することを意味し、random_state=42は分割のランダム性をコントロールするためのシード値です。
    • X_train: 学習データの特徴量
    • X_test: テストデータの特徴量
    • y_tarin: 学習データの目的変数
    • y_test: テストデータの目的変数

このプロセスは機械学習プロジェクトにおいて非常に一般的で、モデルの訓練とその後の性能評価のためにデータを適切に準備するために行われます。学習データはモデルの学習に、テストデータはモデルの汎化能力を評価するために使用されます。

 

　ハイパーパラメータチューニング

では、以下の手順で、変数ごとの関数選択、その各関数や推定器のハイパーパラメータのチューニングを実施します。

1. 関数と変換器クラスの定義
2. Optunaの目的関数の定義
3. ハイパーパラメータチューニングの実施

その結果、パイプラインにとって最適と思われるハイパーパラメータの値（関数選択含む）を出力します。

 

　　関数と変換器クラスの定義

以下、コードです。

# S字曲線関数の定義
def logistic_function(x, L, k, x0):
    return L / (1 + np.exp(-k * (x - x0)))

def hyperbolic_tangent_function(x, A, B, C, D):
    return A * np.tanh(B * x + C) + D

def gompertz_function(x, a, b, c):
    return a * np.exp(-b * np.exp(-c * x))

# カスタム変換器クラス
class CustomSigmoidTransformer(BaseEstimator, TransformerMixin):
    def __init__(self, curve_params=None):
        self.curve_params = curve_params if curve_params is not None else []

    def fit(self, X, y=None):
        return self

    def transform(self, X):
        transformed_X = np.copy(X)
        for i, params in enumerate(self.curve_params):
            curve_type = params.pop('curve_type')
            if curve_type == 'logistic':
                transformed_X[:, i] = logistic_function(X[:, i], **params)
            elif curve_type == 'hyperbolic_tangent':
                transformed_X[:, i] = hyperbolic_tangent_function(X[:, i], **params)
            elif curve_type == 'gompertz':
                transformed_X[:, i] = gompertz_function(X[:, i], **params)
            params['curve_type'] = curve_type
        return transformed_X

 

このコードは、3つのS字曲線関数を定義し、それらを用いてデータを変換するカスタム変換器クラスを作成しています。

曲線関数の定義

• 一般化ロジスティック関数 (Logistic Function):def logistic_function(x, L, k, x0): この関数はロジスティック曲線（S字曲線）を定義しています。パラメータLは曲線の最大値、kは曲線の急峻さを制御し、x0は曲線の中心を表します。ロジスティック関数は成長モデルや確率モデルなどに広く使われます。
• 一般化ハイパボリックタンジェント(Hyperbolic Tangent Function):def hyperbolic_tangent_function(x, A, B, C, D): この関数は双曲線正接（tanh）関数を定義しており、データを変換するための柔軟性を提供します。A, B, C, Dはそれぞれ関数の振幅、スケール、シフト、オフセットを制御します。
• ゴンペルツ関数 (Gompertz Function):def gompertz_function(x, a, b, c): ゴンペルツ関数は成長の減速をモデル化するために使われる関数です。aは漸近線、bとcは成長の速さと形状を決定します。

カスタム変換器クラス

• class CustomSigmoidTransformer(BaseEstimator, TransformerMixin): このクラスは、上記で定義された曲線関数を用いてデータを変換するためのカスタム変換器です。BaseEstimatorとTransformerMixinを継承することで、scikit-learnのパイプラインと互換性を持たせています。
  • __init__メソッドは初期化時に曲線パラメータを受け取ります。
  • fitメソッドは変換器をデータに適合させますが、この場合特に学習を必要としないので、自身をそのまま返します。
  • transformメソッドは実際にデータ変換を行います。入力されたデータXに対して、指定された曲線関数に基づいて変換を行い、変換されたデータを返します。

 

　　Optunaの目的関数の定義

機械学習モデルのハイパーパラメータチューニングに使用されるOptunaの目的関数であるObjectiveを定義します。

Objective関数が長くならないよう（というか、分かりやすくするため）、Objective関数の中で利用する以下の補助関数を別途定義します。

• get_estimator_params:推定器のハイパーパラメータを選択する関数
• get_curve_params:S字曲線のハイパーパラメータを選択する関数
• build_pipeline:パイプラインを構築する関数

 

以下、コードです。

# Optunaによるハイパーパラメータチューニングの関数
def objective(trial, X_data, y_data):
    # S字曲線のパラメータをチューニング
    curves = []
    for i in range(X_data.shape[1]):
        curve_type = trial.suggest_categorical(f"curve_type_{i}", ["logistic", "hyperbolic_tangent", "gompertz"])
        params = get_curve_params(trial, curve_type, i)
        curves.append({'curve_type': curve_type, **params})

    # 推定器のハイパーパラメータを選択
    estimator, estimator_params = get_estimator_params(trial)
    pipeline = build_pipeline(curves, estimator, estimator_params)
    pipeline.fit(X_data, y_data)

    # モデル評価
    predictions = pipeline.predict(X_data)
    return np.mean((y_data - predictions) ** 2)

# objective関数の中で利用する関数

## 推定器のハイパーパラメータを選択する関数
def get_estimator_params(trial):
    estimator_name = trial.suggest_categorical(
        'estimator', 
        ['xgboost', 'decision_tree', 'random_forest']
    )

    if estimator_name == 'xgboost':
        return xgb.XGBRegressor, {
            'learning_rate': trial.suggest_float('xgboost_learning_rate', 0.01, 0.5, log=True),
            'max_depth': trial.suggest_int('xgboost_max_depth', 3, 9),
            'subsample': trial.suggest_float('xgboost_subsample', 0.5, 1.0),
            'colsample_bytree': trial.suggest_float('xgboost_colsample_bytree', 0.5, 1.0),
            'n_estimators': trial.suggest_int('xgboost_n_estimators', 50, 300)
        }
    elif estimator_name == 'decision_tree':
        return DecisionTreeRegressor, {
            'max_depth': trial.suggest_int('decision_tree_max_depth', 1, 9),
            'min_samples_split': trial.suggest_int('decision_tree_min_samples_split', 2, 16),
            'min_samples_leaf': trial.suggest_int('decision_tree_min_samples_leaf', 1, 16)
        }
    elif estimator_name == 'random_forest':
        return RandomForestRegressor, {
            'n_estimators': trial.suggest_int('random_forest_n_estimators', 100, 300),
            'max_depth': trial.suggest_int('random_forest_max_depth', 10, 100),
            'max_features': trial.suggest_categorical('random_forest_max_features', ['auto', 'sqrt']),
            'min_samples_split': trial.suggest_int('random_forest_min_samples_split', 2, 16),
            'min_samples_leaf': trial.suggest_int('random_forest_min_samples_leaf', 1, 16),
            'bootstrap': trial.suggest_categorical('random_forest_bootstrap', [True, False])
        }
    else:
        raise ValueError(f"Invalid estimator name: {estimator_name}")

## S字曲線のハイパーパラメータを選択する関数
def get_curve_params(trial, curve_type, index):
    if curve_type == 'logistic':
        return {
            'L': trial.suggest_float(f"L_{index}", 0.1, 10),
            'k': trial.suggest_float(f"k_{index}", 0.1, 10),
            'x0': trial.suggest_float(f"x0_{index}", -10, 10)
        }
    elif curve_type == 'hyperbolic_tangent':
        return {
            'A': trial.suggest_float(f"A_{index}", 0.1, 10),
            'B': trial.suggest_float(f"B_{index}", 0.1, 10),
            'C': trial.suggest_float(f"C_{index}", -10, 10),
            'D': trial.suggest_float(f"D_{index}", -10, 10)
        }
    elif curve_type == 'gompertz':
        return {
            'a': trial.suggest_float(f"a_{index}", 0.1, 10),
            'b': trial.suggest_float(f"b_{index}", 0.1, 10),
            'c': trial.suggest_float(f"c_{index}", -10, 10)
        }
    else:
        raise ValueError(f"Invalid curve type: {curve_type}")

## パイプラインを構築する関数
def build_pipeline(curve_params, estimator_cls, estimator_params):
    transformer = CustomSigmoidTransformer(curve_params=curve_params)
    estimator = estimator_cls(**estimator_params)
    return Pipeline([
        ('transformer', transformer),
        ('regressor', estimator)
    ])

 

このコードはOptunaを使用して、データ変換と機械学習モデルのハイパーパラメータを同時にチューニングするための関数群を定義しています。

Optunaによるハイパーパラメータチューニングの関数

• objective(trial, X_data, y_data):
  • この関数はOptunaのトライアルごとに呼び出され、ハイパーパラメータの設定を評価します。
  • まず、S字曲線（ロジスティック、ハイボリックタンジェント、ゴンペルツ）のパラメータをチューニングします。これにより、データを特定の曲線関数で変換するためのパラメータが決定されます。
  • 次に、get_estimator_params関数を使用して推定器（機械学習モデル）のハイパーパラメータを選択します。
  • その後、カスタム変換器と推定器を含むパイプラインを構築し、訓練データに適合させます。
  • 最後に、訓練データに対する予測を行い、予測誤差（平均二乗誤差）を計算して返します。この値が最小になるようなハイパーパラメータが選択されることになります。

補助関数

• get_estimator_params(trial):
  • 推定器（XGBoost、決定木、ランダムフォレスト）のハイパーパラメータを選択するための関数です。
  • それぞれの推定器の探索対象のハイパーパラメータ（学習率、深さ、サブサンプル比率など）や探索範囲も定義しています。
• get_curve_params(trial, curve_type, index):
  • S字曲線（ロジスティック、ハイボリックタンジェント、ゴンペルツ）のハイパーパラメータを選択する関数です。
  • 各曲線タイプごとに異なるハイパーパラメータ（L, k, x0など）の探索範囲も定義しています。
• build_pipeline(curve_params, estimator_cls, estimator_params):
  • カスタム変換器と選択された推定器を含むパイプラインを構築する関数です。
  • 変換器は指定された曲線パラメータを使用し、推定器は選択されたハイパーパラメータを使用します。

 

　　ハイパーパラメータチューニングの実施

Optunaを用いて機械学習モデルのハイパーパラメータを、学習データを使いチューニング（設定した試行回数の中で最もいいハイパーパラメータの探索）をしていきます。

以下、コードです。

# Optunaのスタディ作成と実行
study = optuna.create_study(direction="minimize")
study.optimize(
    lambda trial: objective(trial, X_train.values, y_train.values), 
    n_trials=100)

# 最適なパラメータの出力
print("Best trial:")
trial = study.best_trial
print(f"  Value: {trial.value}")
for key, value in trial.params.items():
    print(f"    {key}: {value}")

 

このコードは、Optunaを使用してハイパーパラメータのチューニングを行い、最適なハイパーパラメータを探索します。

Optunaのスタディ作成と実行

• スタディの作成:
  • study = optuna.create_study(direction="minimize"): ここで新しいOptunaのスタディ（実験）が作成されます。
  • direction="minimize"は、このスタディの目的が評価関数の最小化であることを示しています。これは、例えば平均二乗誤差などの損失関数を最小化することを意味します。
• スタディの最適化:
  • study.optimize(lambda trial: objective(trial, X_train.values, y_train.values), n_trials=100): この行はスタディを最適化を行うための命令です。
  • ここでobjective関数が各トライアルごとに呼び出され、指定された回数（n_trials=100）だけ繰り返されます。
  • X_train.valuesとy_train.valuesは訓練データセットの特徴量と目標変数を表しており、これらはobjective関数に渡されます。

最適なパラメータの出力

• 最適化プロセスが完了した後、最も良い結果を出したトライアルの情報が出力されます。
  • print("Best trial:"): これは単に出力のヘッダーを表示しています。
  • trial = study.best_trial: これは最適化プロセスの中で最も良い結果を出したトライアルを取得します。
  • print(f" Value: {trial.value}"): この行はそのトライアルの評価値（例えば損失関数の値）を出力します。
  • for key, value in trial.params.items(): print(f" {key}: {value}"): これは最適なトライアルで使用された各ハイパーパラメータの名前と値を出力します。

 

以下、実行結果です。

Best trial:
  Value: 2.2402685761509593e-07
    curve_type_0: logistic
    L_0: 2.363806609650417
    k_0: 2.239186035279142
    x0_0: 7.229704381505622
    curve_type_1: logistic
    L_1: 2.116296845384312
    k_1: 0.591014354107582
    x0_1: -9.539651837793727
    curve_type_2: logistic
    L_2: 1.666395734987133
    k_2: 3.1812027434417685
    x0_2: -1.2266728357985883
    curve_type_3: logistic
    L_3: 7.344721284508012
    k_3: 1.9424210883578221
    x0_3: 4.308382051162423
    curve_type_4: gompertz
    a_4: 6.698744664295923
    b_4: 1.4404007474188154
    c_4: -0.6625553153493244
    estimator: xgboost
    xgboost_learning_rate: 0.4227212460901749
    xgboost_max_depth: 9
    xgboost_subsample: 0.5562423159030994
    xgboost_colsample_bytree: 0.8972573037349334
    xgboost_n_estimators: 203

 

この結果を簡単に説明します。

• Value:
  • 2.4017594736665816e-07
  • これはトライアルの評価値（おそらく損失関数の値）で、非常に小さい値です。これはモデルが目標変数を非常に正確に予測していることを意味します。
• 曲線タイプとそのパラメータ:
  • 5つの特徴量に対する、それぞれの曲線タイプとそのハイパーパラメータです。
  • 例えばcurve_type_0: logisticは、最初の特徴量がロジスティック曲線で変換され、L_0, k_0, x0_0がそのパラメータです。
• 推定器とそのハイパーパラメータ:
  • estimator: xgboost – このトライアルでは、推定器（機械学習モデル）としてXGBoostが選ばれました。
  • その後の行はXGBoostのハイパーパラメータです。例えば、xgboost_learning_rate: 0.35728408276984996は学習率を示し、xgboost_max_depth: 9は木の最大深度を示します。その他にも、サブサンプル比率、特徴量のサンプル比率、および推定器の数が決定されています。

 

　パイプラインを構築し検証

Optunaによるハイパーパラメータの最適化後、最適なパラメータを使用してモデルを訓練し、テストデータでその性能を評価しています。

　　最適ハイパーパラメータでパイプラインを構築

先ほど見つけたベストなハイパーパラメータを使い、学習データでパイプラインを構築します。

パイプラインを構築する前に、先ほど見つけたベストなハイパーパラメータを取得する関数を定義します。

以下、コードです。

# S字曲線の最適なハイパーパラメータを取得する関数
def get_curve_params_from_trial(trial, index):
    curve_type = trial.params.get(f"curve_type_{index}")

    if curve_type == 'logistic':
        return {
            'curve_type': curve_type,
            'L': trial.params.get(f"L_{index}"),
            'k': trial.params.get(f"k_{index}"),
            'x0': trial.params.get(f"x0_{index}")
        }
    elif curve_type == 'hyperbolic_tangent':
        return {
            'curve_type': curve_type,
            'A': trial.params.get(f"A_{index}"),
            'B': trial.params.get(f"B_{index}"),
            'C': trial.params.get(f"C_{index}"),
            'D': trial.params.get(f"D_{index}")
        }
    elif curve_type == 'gompertz':
        return {
            'curve_type': curve_type,
            'a': trial.params.get(f"a_{index}"),
            'b': trial.params.get(f"b_{index}"),
            'c': trial.params.get(f"c_{index}")
        }
    else:
        raise ValueError(f"Invalid curve type: {curve_type}")

# 推定器の最適なハイパーパラメータを取得する関数
def get_estimator_params_from_trial(trial):
    estimator_name = trial.params.get("estimator")

    if estimator_name == 'xgboost':
        return xgb.XGBRegressor, {
            'learning_rate': trial.params.get("xgboost_learning_rate"),
            'max_depth': trial.params.get("xgboost_max_depth"),
            'subsample': trial.params.get("xgboost_subsample"),
            'colsample_bytree': trial.params.get("xgboost_colsample_bytree"),
            'n_estimators': trial.params.get("xgboost_n_estimators")
        }
    elif estimator_name == 'decision_tree':
        return DecisionTreeRegressor, {
            'max_depth': trial.params.get("decision_tree_max_depth"),
            'min_samples_split': trial.params.get("decision_tree_min_samples_split"),
            'min_samples_leaf': trial.params.get("decision_tree_min_samples_leaf")
        }
    elif estimator_name == 'random_forest':
        return RandomForestRegressor, {
            'n_estimators': trial.params.get("random_forest_n_estimators"),
            'max_depth': trial.params.get("random_forest_max_depth"),
            'max_features': trial.params.get("random_forest_max_features"),
            'min_samples_split': trial.params.get("random_forest_min_samples_split"),
            'min_samples_leaf': trial.params.get("random_forest_min_samples_leaf"),
            'bootstrap': trial.params.get("random_forest_bootstrap")
        }
    else:
        raise ValueError(f"Invalid estimator name: {estimator_name}")

 

このコードは、Optunaの最適化プロセスで得られた結果から、S字曲線のハイパーパラメータと推定器（機械学習モデル）のハイパーパラメータを取得するための関数を定義しています。

S字曲線の最適なハイパーパラメータを取得する関数

• get_curve_params_from_trial(trial, index):
  • この関数は、指定されたトライアルと特徴量のインデックスに基づいて、S字曲線のパラメータを取得します。
  • curve_typeをトライアルから取得し、そのタイプに基づいて一般化ロジスティック関数、一般化ハイパボリックタンジェント関数、およびゴンペルツ関数のパラメータを辞書形式で返します。
  • 例えば、一般化ロジスティック曲線の場合、L, k, x0 の値を取得し、それらを含む辞書を返します。

推定器の最適なハイパーパラメータを取得する関数

• get_estimator_params_from_trial(trial):
  • この関数は、トライアルから推定器の名前を取得し、選択された推定器のハイパーパラメータを取得します。
  • 推定器の名前に基づいて、XGBoost、決定木、またはランダムフォレストのいずれかの推定器クラスと、それに関連するハイパーパラメータの辞書を返します。
  • 例えば、XGBoostが選ばれた場合、learning_rate, max_depth, subsample, colsample_bytree, n_estimators の値を取得します。

 

学習データでパイプラインを構築します。

以下、コードです。

# 最適なパイプラインの構築
optimal_curves = [
    get_curve_params_from_trial(trial, i) 
    for i in range(X_train.shape[1])]
estimator_name, estimator_params = get_estimator_params_from_trial(trial)

optimal_pipeline = build_pipeline(
    optimal_curves, 
    estimator_name, estimator_params)

optimal_pipeline.fit(X_train.values, y_train.values)

 

このコードは、Optunaの最適化プロセスで得られた最適なハイパーパラメータを使用して、最適化された機械学習パイプラインを構築します。

• 最適なS字曲線パラメータの取得:
  • optimal_curves = [get_curve_params_from_trial(trial, i) for i in range(X_train.shape[1])]: この行はリスト内包表記を使用して、訓練データの各特徴量（X_train.shape[1]は特徴量の数を表します）に対して最適な曲線パラメータを取得しています。
  • get_curve_params_from_trial関数は、Optunaのトライアル結果から特定の特徴量に対する最適な曲線パラメータを返します。
• 最適な推定器とそのパラメータの取得:
  • estimator_name, estimator_params = get_estimator_params_from_trial(trial): この行は、Optunaのトライアル結果から選択された最適な推定器とそのハイパーパラメータを取得します。
• 最適なパイプラインの構築:
  • optimal_pipeline = build_pipeline(optimal_curves, estimator_name, estimator_params): この行は、取得した最適なS字曲線ハイパーパラメータと推定器ハイパーパラメータを使用して、データ変換とモデル推定のためのパイプラインを構築します。
  • build_pipeline関数はカスタム変換器（CustomSigmoidTransformerを使用して各特徴量を変換）と推定器（estimator_nameに基づいて選択）を組み合わせてパイプラインを作成します。
• パイプラインの訓練:
  • optimal_pipeline.fit(X_train.values, y_train.values): この行は、構築されたパイプラインを学習データ（X_trainとy_train）に適合させます。
  • これにより、パイプライン内の変換器と推定器が訓練され、モデルが学習されます。

このコードで、最適化されたハイパーパラメータを使用してパイプラインを構築しそれを学習データに適合させることができます。このハイプラインは、予測で利用することができます。

 

　　最適なパイプラインで予測し検証

以下、コードです。

# 最適なパイプラインを使って予測を生成
predicted_y = optimal_pipeline.predict(X_test.values)

# 評価指標を計算
mae = mean_absolute_error(y_test, predicted_y)
mape = mean_absolute_percentage_error(y_test, predicted_y)
r2 = r2_score(y_test, predicted_y)

print('MAE:',mae)
print('MAPE:',mape,'%')
print('R2:',r2)

 

このコードで、最適化された機械学習パイプラインを使用してテストデータに対する予測を行い、その予測結果を評価した結果を出力します。

最適なパイプラインを使って予測を生成

• predicted_y = optimal_pipeline.predict(X_test.values): 最適化されたパイプライン（optimal_pipeline）を使用して、テストデータセット（X_test）に基づいて予測を生成します。
• predicted_yは、モデルによって予測された目標変数の値です。

評価指標を計算

• mae = mean_absolute_error(y_test, predicted_y): 平均絶対誤差（MAE）を計算します。これは、実際の値と予測値との差の絶対値の平均で、予測の精度を測る一般的な指標です。
• mape = mean_absolute_percentage_error(y_test, predicted_y): 平均絶対パーセンテージ誤差（MAPE）を計算します。これは、実際の値に対する予測の誤差の割合を示し、予測の相対的な誤差を測定します。
• r2 = r2_score(y_test, predicted_y): 決定係数（R²）を計算します。これは、モデルがデータの変動をどれだけ説明しているかを示す指標で、1に近いほど良い予測性能を示します。

結果の出力

• print('MAE:',mae): 平均絶対誤差の値を出力します。
• print('MAPE:',mape,'%'): 平均絶対パーセンテージ誤差の値をパーセンテージとして出力します。
• print('R2:',r2): 決定係数の値を出力します。

 

以下、実行結果です。

MAE: 0.24329977996127586
MAPE: 1.0445372098487296 %
R2: 0.9631467022253833

 

簡単に結果を説明します。

• MAE (平均絶対誤差): 0.23215722409001188
  • MAEは予測値と実際の値の差の絶対値の平均です。この値は、モデルが平均して予測を実際の値からどの程度外れているかを示します。
  • この場合、MAEが0.232という値は、予測が平均して実際の値から0.232の差であることを意味します。
  • MAEは低いほど良いとされ、このモデルのMAEは比較的低い値です。
• MAPE (平均絶対パーセンテージ誤差): 1.0656549586233992%
  • MAPEは予測誤差の割合を示し、モデルの予測が実際の値に対してどれだけの割合で外れているかを表します。
  • この場合、MAPEが約1.07%であることは、予測が実際の値から平均して約1.07%外れていることを意味します。
  • 一般に、MAPEも低いほど良いとされ、このモデルは非常に正確な予測をしていることを示唆しています。
• R² (決定係数): 0.9683269621378233
  • R²はモデルがデータのどれだけの変動を説明できているかを示す指標です。
  • R²の値が1に近いほど、モデルがデータの変動を良く捉えていることを示します。
  • この場合、R²が約0.968と非常に高いため、モデルはテストデータの変動の大部分を効果的に説明していると言えます。

この結果は、モデルがテストデータに対して非常に高い予測精度を持っていることを示しています。MAEとMAPEの低い値は予測の精度が高いことを示し、R²の高い値はモデルがデータの変動をよく捉えていることを意味します。このような結果は、モデルが実際のアプリケーションやビジネス上の意思決定において信頼できる予測を提供できることを示唆しています。

 

　　散布図（実測×予測）

テストデータの、実際の値と予測された値の関係を視覚的に示す散布図を作成しています。

以下、コードです。

plt.figure(figsize=(10,8))
plt.scatter(y_test, predicted_y, alpha=0.7)
plt.plot(
    [y_test.min(), y_test.max()], 
    [predicted_y.min(), predicted_y.max()], 
    color='red')
plt.xlabel('Actual')
plt.ylabel('Predicted')
plt.title('Actual vs Predicted')
plt.show()

 

このコードで、実際の値（y_test）と予測値（predicted_y）を比較するための散布図を作成し表示します。

• plt.figure(figsize=(10,8)): この行は、プロットする図のサイズを幅10インチ、高さ8インチに設定しています。
• plt.scatter(y_test, predicted_y, alpha=0.7): この行は散布図を作成します。ここでは実際の値y_testをx軸に、予測値predicted_yをy軸にプロットしています。alpha=0.7はプロットの点の透明度を設定し、重なり合う点を見やすくしています。
• plt.plot([y_test.min(), y_test.max()], [predicted_y.min(), predicted_y.max()], color='red'): この行は実際の値と予測値が完全に一致する場合の線（理想的な1:1の関係）を赤色で描画しています。y_test.min()からy_test.max()までの範囲とpredicted_y.min()からpredicted_y.max()までの範囲で線を引いています。
• plt.xlabel('Actual')とplt.ylabel('Predicted'): これらの行は、x軸とy軸にそれぞれ「Actual」（実際の値）と「Predicted」（予測値）というラベルを設定しています。
• plt.title('Actual vs Predicted'): この行はグラフに「Actual vs Predicted」というタイトルを付けています。
• plt.show(): この行はプロットしたグラフを表示します。

 

以下、実行結果です。

 

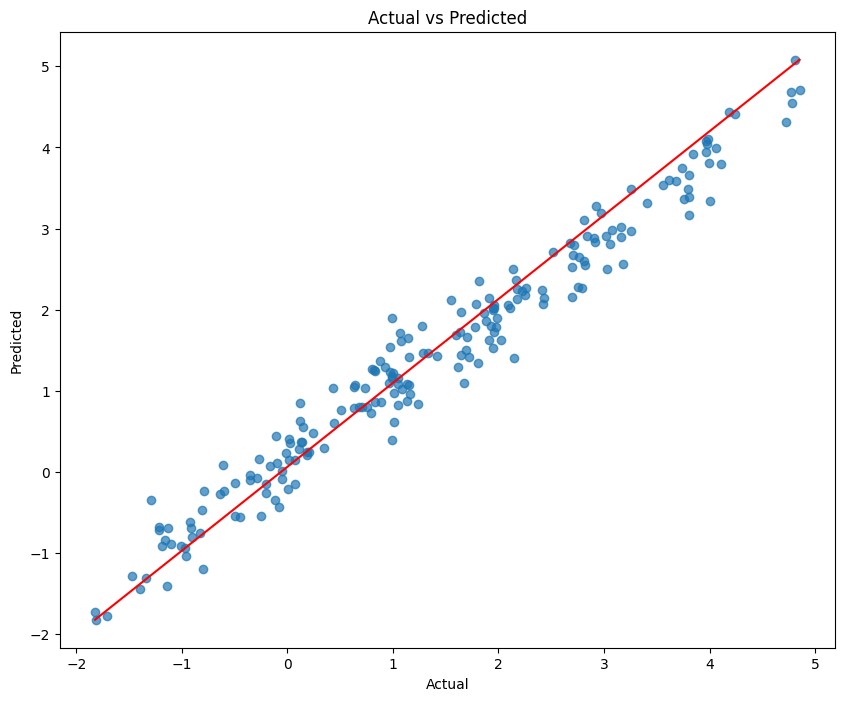
この散布図は、モデルの予測値が実際の値とどの程度一致しているかを視覚的に評価するためのものです。

点が赤い線（理想的な1:1の関係）に近いほど、予測が実際の値に近いことを意味し、モデルの予測精度が高いことを示します。逆に、赤い線から離れている点は予測誤差が大きいことを示しています。

このような視覚的表現は、モデルの性能を理解し、どのようなデータポイントで予測がうまくいっているか、またはいっていないかを把握するのに役立ちます。

 

まとめ

今回は、さらに推定器も自動選択し、選択した推定器のハイパーパラメータもチューニングする方法についてお話ししました。

ここまでくると、ちょっとした簡易AutoML（自動機械学習）ですね。

特徴量（説明変数）に対する変数変換のための関数や、推定器を増やし拡張してみてください。