- 問題
- 答え
- 解説
- 時系列間の距離測定法
- 時系列距離ライブラリfastdtw
Python コード:
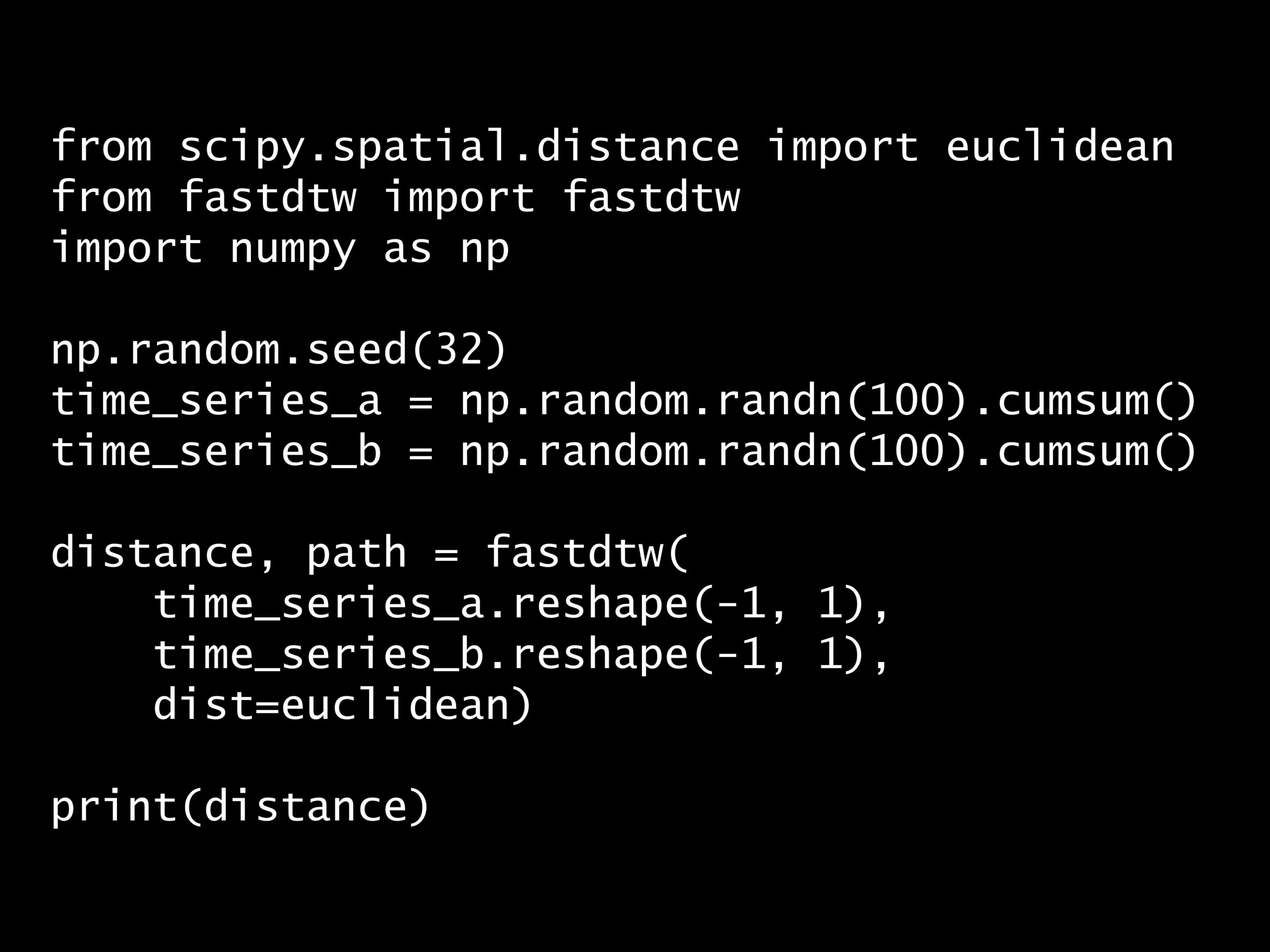
from scipy.spatial.distance import euclidean
from fastdtw import fastdtw
import numpy as np
np.random.seed(32)
time_series_a = np.random.randn(100).cumsum()
time_series_b = np.random.randn(100).cumsum()
distance, path = fastdtw(
time_series_a.reshape(-1, 1),
time_series_b.reshape(-1, 1),
dist=euclidean)
print(distance)
回答の選択肢:
(A) 2つの時系列間のマハラノビス距離
(B) 2つの時系列間のダイナミックタイムワーピング距離
(C) 2つの時系列間のピアソン相関距離
(D) 2つの時系列間のマンハッタン距離
311.49187352909786
正解: (B)
回答の選択肢:
(A) 2つの時系列間のマハラノビス距離
(B) 2つの時系列間のダイナミックタイムワーピング距離
(C) 2つの時系列間のピアソン相関距離
(D) 2つの時系列間のマンハッタン距離
from scipy.spatial.distance import euclidean
from fastdtw import fastdtw
import numpy as np
np.random.seed(32)
time_series_a = np.random.randn(100).cumsum()
time_series_b = np.random.randn(100).cumsum()
distance, path = fastdtw(
time_series_a.reshape(-1, 1),
time_series_b.reshape(-1, 1),
dist=euclidean)
print(distance)
DTWは、二つの時系列間の類似性を測定するための手法であり、特に、形状は似ているが時間軸における拡大・縮小やシフトが発生している場合に有用です。
詳しく説明します。
numpyの乱数生成器を使って2つの時系列データtime_series_aとtime_series_bを生成します。
np.random.seed(32) time_series_a = np.random.randn(100).cumsum() time_series_b = np.random.randn(100).cumsum()
time_series_aに格納されているデータは次のようになっています。
[-0.34889445 0.63480898 1.21573181 1.28601625 2.06354893 2.64550768 4.1172982 5.78047921 5.51930209 4.83062528 4.13570201 6.07612547 7.88154066 8.33785452 7.76304248 7.87722298 9.39080375 9.74193559 9.65300238 10.5699566 11.07560173 10.26033062 10.64948157 10.2245191 10.26414225 9.73617833 9.22587465 8.3375895 9.42521424 10.0986065 9.03128946 10.24933945 13.61305199 12.78079859 12.44045021 10.58187867 10.58270173 10.93427622 12.45578506 11.77531093 12.71336863 12.03195392 11.83085584 11.81336719 10.02545506 9.17371484 7.54541153 8.51240927 8.56552486 8.85523779 8.91768213 7.8195534 7.95008646 7.7647494 6.42401467 6.09999499 7.58435837 8.89744665 8.26528264 7.87370934 5.50521364 4.91452972 3.2015282 1.88867679 2.34245639 0.5591311 1.98464693 1.63894833 2.63760576 3.3629921 2.4345824 1.75459966 0.64197122 0.65444638 0.12813503 -0.55139587 0.90855174 2.27512532 3.98322667 4.22225709 3.7623225 4.92063421 5.17430815 5.37805111 7.15125267 8.13986195 7.32843477 5.80517528 5.5041808 5.11356977 5.58160692 7.09515534 7.51979545 7.64214167 6.25449455 5.78745345 7.06105008 7.1827717 5.96530748 6.36859558]
fastdtw関数(fastdtwパッケージ)を使ってDTW距離とパスを計算しています。この関数に、今作った二つの時系列データと距離計算関数(ここではユークリッド距離)を指定しています。
distance, path = fastdtw(
time_series_a.reshape(-1, 1),
time_series_b.reshape(-1, 1),
dist=euclidean)
ちなみに、reshape(-1, 1)は、NumPyの配列の形状を変形(リシェープ)し、fastdtw関数が受け取れるようにしています。
具体的には、reshape(-1, 1)は配列を1列の2次元配列(列ベクトル)にリシェープします。ここで、-1 は他の次元のサイズを保持しつつ可能な限りその次元を変形することを指示しています。
このケースでは、time_series_aは一次元配列として生成されます。このままだと、fastdtw関数はこのデータを受け取れません。そのため、reshape(-1, 1)を使用することで一次元配列を一列の二次元配列に変形し、fastdtw関数に渡しています。
以下、リシェープ後のtime_series_aです。つまりtime_series_a.reshape(-1, 1)です。
array([[-0.34889445],
[ 0.63480898],
[ 1.21573181],
[ 1.28601625],
[ 2.06354893],
[ 2.64550768],
[ 4.1172982 ],
[ 5.78047921],
[ 5.51930209],
[ 4.83062528],
[ 4.13570201],
[ 6.07612547],
[ 7.88154066],
[ 8.33785452],
[ 7.76304248],
[ 7.87722298],
[ 9.39080375],
[ 9.74193559],
[ 9.65300238],
[10.5699566 ],
[11.07560173],
[10.26033062],
[10.64948157],
[10.2245191 ],
[10.26414225],
[ 9.73617833],
[ 9.22587465],
[ 8.3375895 ],
[ 9.42521424],
[10.0986065 ],
[ 9.03128946],
[10.24933945],
[13.61305199],
[12.78079859],
[12.44045021],
[10.58187867],
[10.58270173],
[10.93427622],
[12.45578506],
[11.77531093],
[12.71336863],
[12.03195392],
[11.83085584],
[11.81336719],
[10.02545506],
[ 9.17371484],
[ 7.54541153],
[ 8.51240927],
[ 8.56552486],
[ 8.85523779],
[ 8.91768213],
[ 7.8195534 ],
[ 7.95008646],
[ 7.7647494 ],
[ 6.42401467],
[ 6.09999499],
[ 7.58435837],
[ 8.89744665],
[ 8.26528264],
[ 7.87370934],
[ 5.50521364],
[ 4.91452972],
[ 3.2015282 ],
[ 1.88867679],
[ 2.34245639],
[ 0.5591311 ],
[ 1.98464693],
[ 1.63894833],
[ 2.63760576],
[ 3.3629921 ],
[ 2.4345824 ],
[ 1.75459966],
[ 0.64197122],
[ 0.65444638],
[ 0.12813503],
[-0.55139587],
[ 0.90855174],
[ 2.27512532],
[ 3.98322667],
[ 4.22225709],
[ 3.7623225 ],
[ 4.92063421],
[ 5.17430815],
[ 5.37805111],
[ 7.15125267],
[ 8.13986195],
[ 7.32843477],
[ 5.80517528],
[ 5.5041808 ],
[ 5.11356977],
[ 5.58160692],
[ 7.09515534],
[ 7.51979545],
[ 7.64214167],
[ 6.25449455],
[ 5.78745345],
[ 7.06105008],
[ 7.1827717 ],
[ 5.96530748],
[ 6.36859558]]))
fastdtw関数の結果として、以下のdistanceとpathが出力されます。
distance:DTW距離- DTW距離は、2つの時系列データ間の類似度を量化したものです。
- DTW距離が小さいほど、2つの時系列データは互いに似ていると判断されます。
- パターンマッチングやクラスタリング、異常検知などのタスクにおいて、この時系列データ間の類似度指標が使用されます。
path:DTWアルゴリズムが見つけた最適な対応付け(マッチング)- 一方の時系列データの各点が、もう一方の時系列データのどの点と対応付けられたかを示します。
- 例えば、`path[i] = (j, k)`というエントリは、1つ目の時系列データの`j`番目の要素が、2つ目の時系列データの`k`番目の要素と一致することを示します。
- 異なる時間スケールや速度で進行する時系列データ間の類似性を評価する際に、この`path`が役立ちます。
DTW距離distanceを表示します。
print(distance)
311.49187352909786
ユークリッド距離 (Euclidean Distance)
ユークリッド距離は、最も基本的な距離測定法の一つです。時系列データをベクトルとして扱い、二つの時系列ベクトル間の直線距離を計算します。式は以下の通りです。
マンハッタン距離 (Manhattan Distance)
マンハッタン距離は、ベクトルの成分の絶対値の差の総和として定義されます。これは、ユークリッド距離よりも外れ値の影響を受けにくいとされています。
ダイナミックタイムワーピング (Dynamic Time Warping, DTW)
DTWは、時系列間の類似性を測定するための技術で、二つの時系列が異なる時間スケールで伸縮する場合でも比較できます。DTWは、時系列間の最小距離を見つけ出すことで、形状の類似性に基づいた比較を可能にします。
マハラノビス距離 (Mahalanobis Distance)
マハラノビス距離は、データの分布を考慮した距離測定法です。異なるスケールや相関を持つデータ間の「真の」距離を測ることができます。時系列データに適用する場合は、データの共分散構造を考慮する点が特徴です。
コサイン類似度 (Cosine Similarity)
コサイン類似度は、二つの時系列間の角度のコサインを用いて類似性を測定します。値は-1から1の範囲を取り、1に近いほど類似度が高いことを示します。方向性の類似性を測るため、大きさが異なる時系列データの比較に適しています。
ピアソン相関係数 (Pearson Correlation Coefficient)
ピアソン相関係数は、二つの時系列間の線形相関を測定します。-1から1の範囲の値を取り、1は完全な正の相関、-1は完全な負の相関を意味します。
ロングエスト・コモン・サブシーケンス (Longest Common Subsequence: LCSS)
LCSSは、二つの時系列間で最長の共通の部分列を見つけることに基づく測定法です。この方法は、DTWよりも一部の外れ値に対して鈍感であり、ある程度の時間的シフトに対しても柔軟性があります。
シェイプレットマッチング (Shapelet Matching)
シェイプレットは、時系列データ内の形状を特徴づける部分列です。シェイプレットマッチングは、ある時系列データセット内の形状が他の時系列データセット内でどの程度類似しているかを測る方法です。この手法は、特に時系列分類問題で有用です。
DTW(ダイナミックタイムワーピング)にも、幾つか発展版があります。
時間制約付きダイナミックタイムワーピング (Constrained DTW)
時間制約付きDTWは、DTWのバリエーションで、検索ウィンドウを制限して計算コストを削減します。この制約により、時系列間のマッチングが特定の時間枠内でのみ行われ、計算効率が向上する一方で、時系列データの局所的な伸縮に対しては柔軟に対応します。
サブシーケンスDTW (Subsequence DTW)
サブシーケンスDTWは、ある時系列が別の時系列のサブシーケンスとしてどの程度類似しているかを測定します。これは、特に時系列データ内でパターンや動きを検出する場合に有効です。時系列の一部分が他の時系列内でどの程度マッチするかを評価するため、全体の長さが異なるデータに対しても適用可能です。
マルチスケールDTW (Multiscale DTW)
マルチスケールDTWは、時系列データを複数のスケール(解像度)で解析し、それぞれのスケールでDTWを適用する方法です。このアプローチにより、異なる時間スケールでのパターンの類似性を捉えることができます。時系列データの大きな構造と小さな動きの両方を同時に評価することが可能になります。
ソフトDTW (Soft-DTW)
ソフトDTWは、DTWの損失関数に微分可能なソフトミニマムを使用することで、DTWの計算を滑らかにし、勾配ベースの最適化が可能になる方法です。これにより、機械学習モデルのトレーニングにおいて、時系列データの類似性を直接的な損失関数として組み込むことが可能になります。
fastdtwはPythonで利用可能なライブラリで、ダイナミックタイムワーピング(Dynamic Time Warping, DTW)の計算を高速化するための手法です。
DTWは時系列データ間の類似度を測定する際に広く使用されるアルゴリズムで、異なる長さや速度で観測された時系列データ間の類似性を評価できます。
しかし、通常のDTWアルゴリズムは計算コストが高いため、大規模データセットやリアルタイム処理には適用が難しい場合があります。
特徴
fastdtwは、この計算コストの問題を解決するために開発されました。以下にその主な特徴を紹介します。
- 近似アルゴリズム:
fastdtwは、完全なDTWの計算結果に非常に近い近似解を提供しますが、計算コストは大幅に削減されます。これは、元の時系列データをより低い解像度に縮小し、縮小されたデータに対してDTWを適用することで実現されます。その後、より詳細な解析のために解像度を段階的に上げていきます。 - 効率的な計算:
fastdtwにより、大規模な時系列データセットやリアルタイム処理が必要なアプリケーションでのDTWの利用が可能になります。計算コストの削減は、特にデータが大量にある場合や、高速な処理が求められる場合に有利です。 - 汎用性: さまざまな種類の時系列データに適用可能で、金融、医療、音声認識、ジェスチャー認識など、多岐にわたる分野での応用が期待されます。
使用方法
fastdtwを使用するには、まずPython環境にライブラリをインストールする必要があります。通常、pipコマンドを使用して簡単にインストールできます。
pip install fastdtw
インストール後、fastdtwを使用して時系列データ間の距離を計算する基本的なコードは以下のようになります。
from fastdtw import fastdtw
from scipy.spatial.distance import euclidean
# 2つの時系列データの例
x = [1, 2, 3, 4, 5]
y = [2, 3, 4]
# fastdtwを使用して距離と経路を計算
distance, path = fastdtw(x, y, dist=euclidean)
print("Distance:", distance)
print("Path:", path)
この例では、euclidean(ユークリッド距離)を距離計算の基準として使用していますが、他の距離計算方法も適用可能です。fastdtwは、2つの時系列間の類似度を効率的に計算し、その結果を距離とマッチングパスの形で提供します。
引数の説明
fastdtw関数の引数です。
x: 第一の入力時系列データです。y: 第二の入力時系列データです。radius: 計算の際に考慮される近傍の大きさを定義します。デフォルト値は1です。dist: 2つの時系列ポイント間の距離を計算するための関数または文字列を指定します。文字列の場合、利用可能なオプションはeuclidean、manhattan、chebyshev、minkowskiなどです。デフォルト値はeuclideanです。
関数は最終的に2つの値を返します。
- 最初の値は
xとyの間のDTW距離distanceです。 - 二つ目の値は、最適な対応付け(ワーピングパス)を示すリスト
pathです。
radiusについて簡単にもう少し説明します。
radiusパラメータはダイナミックタイムワーピング(DTW)アルゴリズムにおいて、各時点でどの程度まで時間を「ずらす」ことを許容するかを指定します。
例えば……
radius=0の場合:「ずらし」は許容されず、各時点は同じ時間の点とのみマッチングを行います。radius=1の場合:各時点で1つ前後の時間に対応する点とマッチングを行うことができます。radius=10の場合:各時点で10つ前後の時間に対応する点とマッチングを行うことができます。
要するに、radiusが大きい場合には、より多くのポイントが近傍に含まれるため、より多くのワーピングパスが考慮され、結果としてDTW距離の計算がより精度高く(より正確に)なります。しかし、計算にはより多くの時間が必要となります。
一方、radiusが小さい場合、近傍に含まれるポイントが少なくなるため、考慮されるワーピングパスの数が減少します。これによりDTW距離の計算はより早く、また大まかになります。
distについて簡単にもう少し説明します。
distパラメータで指定可能なeuclidean、manhattan、chebyshev、minkowskiは、二つのベクトルまたはポイント間の距離を計算するための距離関数(または距離メトリクス)です。
euclidean:ユークリッド距離は、もっとも一般的に使用される距離メトリクスで、二つのポイント間の「直線距離」を計算します。n次元空間における二点間のユークリッド距離は、各次元における差の二乗を合計し、その平方根をとることで計算されます。manhattan:マンハッタン距離(またはシティブロック距離)は、各次元における差の絶対値を合計することで二点間の距離を計算します。これはグリッド上の移動距離を計算するような場合に適しており、名前は「マンハッタンのグリッド状の道路網に沿って移動するときの距離」というイメージから来ています。chebyshev:チェビシェフ距離は、距離の測定法の一つで、無限次元ノルムとも呼ばれます。各次元における差の絶対値の最大値を距離として計算します。minkowski:ミンコウスキー距離は、ユークリッド距離とマンハッタン距離を一般化した距離メトリクスで、パラメータpによってこれらを切り替えることができます。p=2の時、ミンコフスキー距離はユークリッド距離と等しくなり、p=1の時、マンハッタン距離と等しくなります。
それぞれの距離関数は、異なる種類の問題やデータの特性に対して適しています。適切な距離関数の選択は、データの理解と、それをどのように利用するかに大いに依存しますので、ご注意ください。