データを活用したマーケティング戦略は、ビジネスの成功に不可欠です。その中心に位置するのが、マーケティングミックスモデリング(MMM)です。
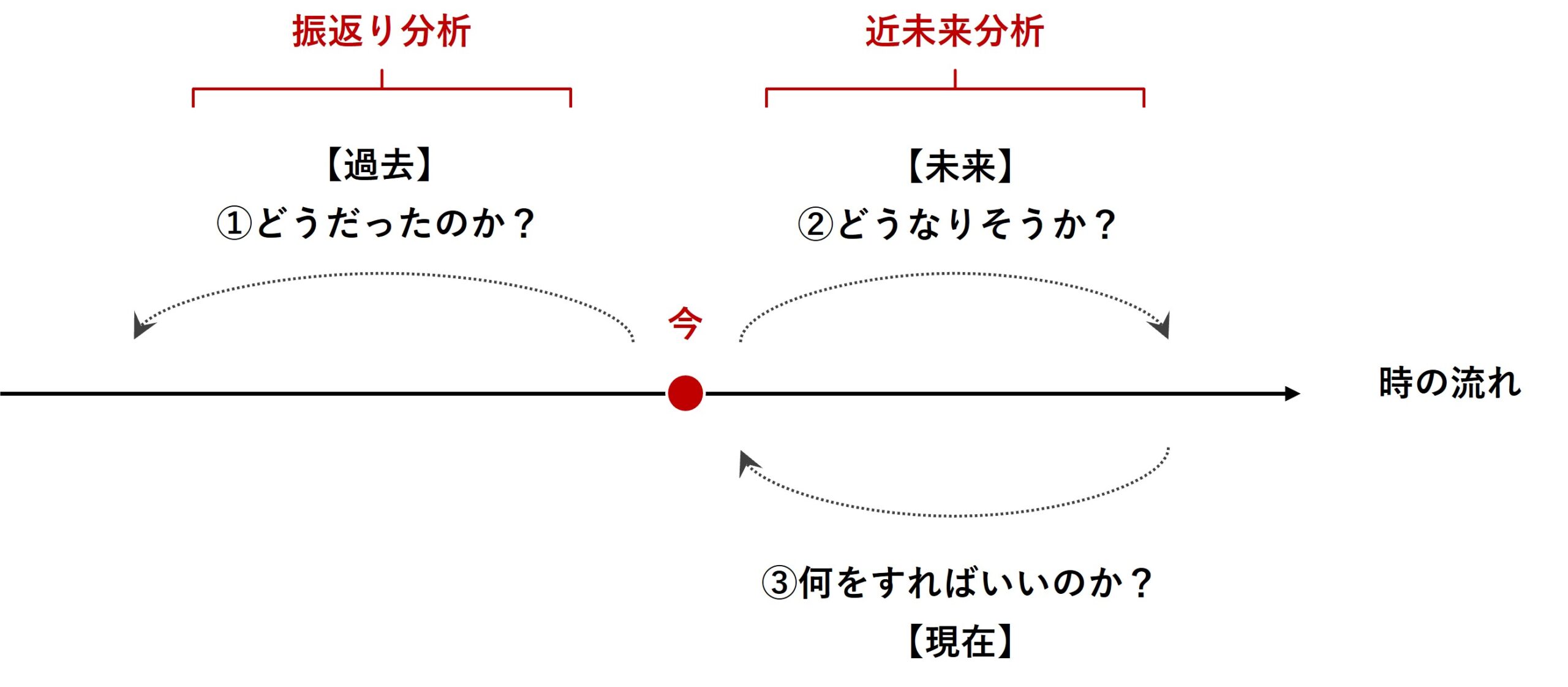
マーケティングミックスモデリング(MMM)は、過去のデータを分析する「振り返り分析」と未来のトレンドを予測する「近未来分析」の両方で有効に活用される強力なツールです。
通常のMMMは、アドストック(Ad Stock)が考慮されます。ここで言うアドストック(Ad Stock)とは、キャリーオーバー効果や飽和効果のことです。
MMMにアドストック(Ad Stock)を組み込むには、パイプラインを構築するといいでしょう。このようなパイプラインを、ここではMMMパイプラインと表現することにします。
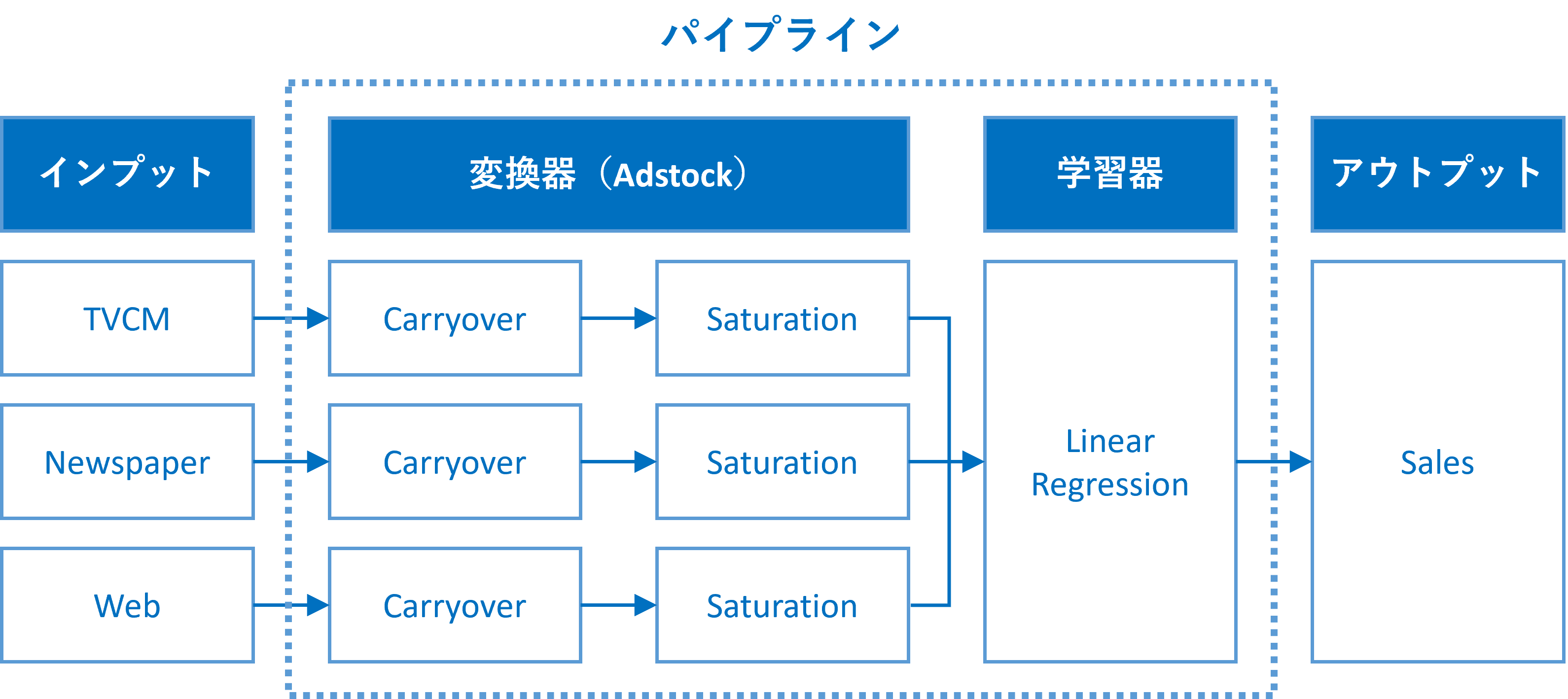
このMMMパイプラインは、少なくとも2つの変換器と1つの推定器が必要になります。
- 変換器
- キャリーオーバー効果関数(Carryover)
- 飽和関数(Saturation)
- 推定器
- 線形回帰系のモデル(Linear Regression):今回はRidge回帰を利用
ここまでの記事(前回と前々回)で、2つのキャリーオーバー効果関数と、2つの飽和関数を紹介しました。
飽和関数は、前回の飽和関数(指数型)と、今回の飽和関数(ロジスティック型)で別のものを定義し使いました。
以下は、飽和関数(指数型)です。
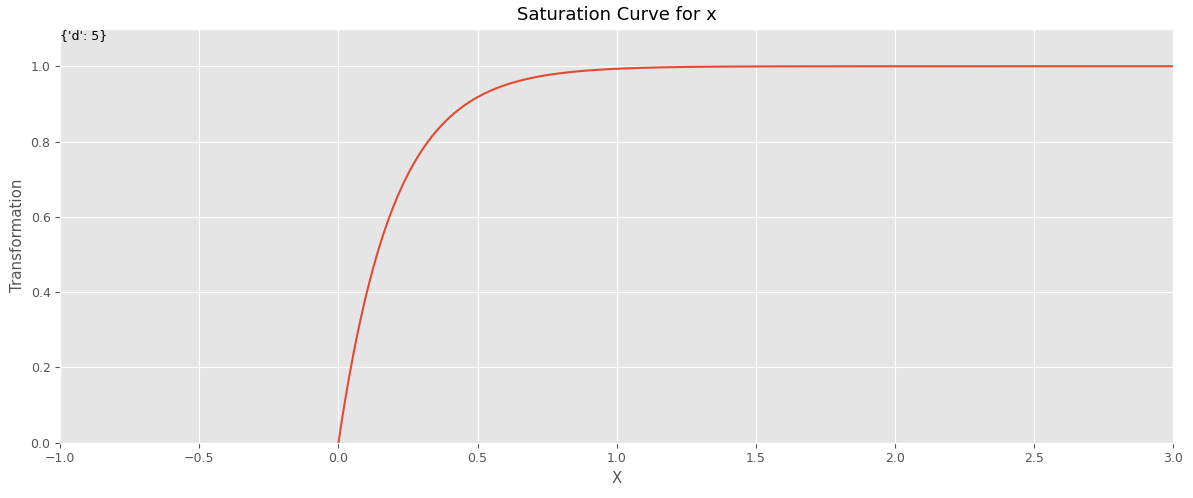
以下は、飽和関数(ロジスティック型)です。
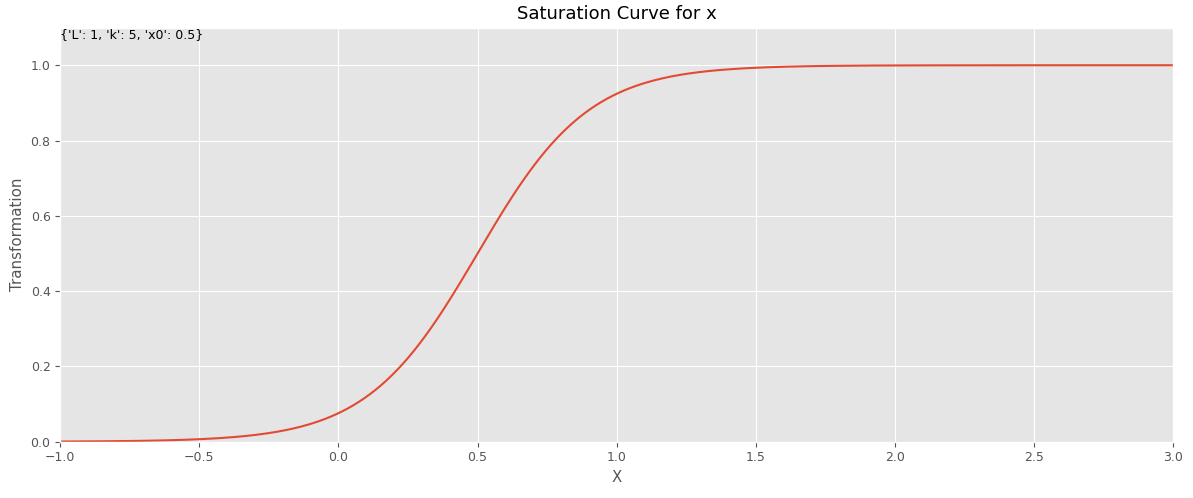
このように飽和関数には他にも色々なものがあります。どれが最適なのでしょうか?
分かりません。データによって異なります。
そこで今回は、アドストックの飽和関数を自動選択し構築するMMMというお話しをします。
具体的には、飽和関数(指数型)と飽和関数(ロジスティック型)のどちらかを自動選択できるように、アドストックのハイパーパラメータに、飽和関数の選択も含めます。
一方、キャリーオーバー効果関数はどうでしょうか?
前回のキャリーオーバー効果関数は、前々回のキャリーオーバー効果関数を一般化したものなので、前回のキャリーオーバー効果関数だけで十分です。
そのため、今回は、前回のキャリーオーバー効果関数を使います。
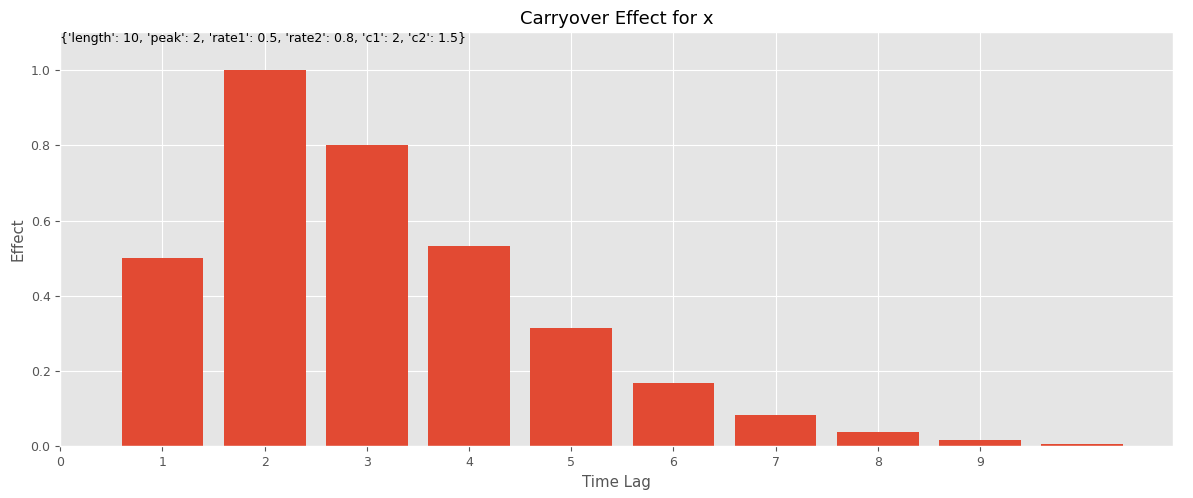
今回は、キャリーオーバー効果関数や飽和関数の数式などの説明はしません。気になる方は、前回と前々回の記事を一読ください。
また、コードの説明も、前回とほぼ同じコードについては説明を省きます。ただ、前回までに登場していないコードのみ説明を加えます。
Contents [hide]
準備
今回利用するモジュールやデータセットの読み込み、先ほど述べたアドストック系関数の定義などを実施していきます。
モジュールなどの読み込み
モジュール
以下、コードです。
import numpy as np
import pandas as pd
import optuna
from sklearn.linear_model import Ridge
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import TimeSeriesSplit
from sklearn.model_selection import cross_val_score
from functools import partial
import warnings
warnings.simplefilter('ignore')
import matplotlib.pyplot as plt
plt.style.use('ggplot') #グラフスタイル
plt.rcParams['figure.figsize'] = [12, 7] #グラフサイズ
plt.rcParams['font.size'] = 9 #フォントサイズ
前々前回作った関数群(MMM構築・評価など)
さらに今回は、前々前回作った以下の関数群を使います。
- MMM構築
train_and_evaluate_model:MMMの構築plot_actual_vs_predicted:構築したMMMの予測値の時系列推移
- 後処理(結果の出力)
calculate_and_plot_contribution:売上貢献度の算出(時系列推移)summarize_and_plot_contribution:売上貢献度構成比の算出calculate_marketing_roi:マーケティングROIの算出
以下からダウンロードできます。
mmm_functions.py ※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/oi17
興味のある方、詳細を知りたい方は、以下を参照ください。
mmm_functions.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。
以下のコードで呼び出せます。
from mmm_functions import *
上手くいかないときは、mmm_functions.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。
データセットの読み込み
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
目的変数y(売上)をプロットします。
以下、コードです。
y.plot() plt.show()
以下、実行結果です。
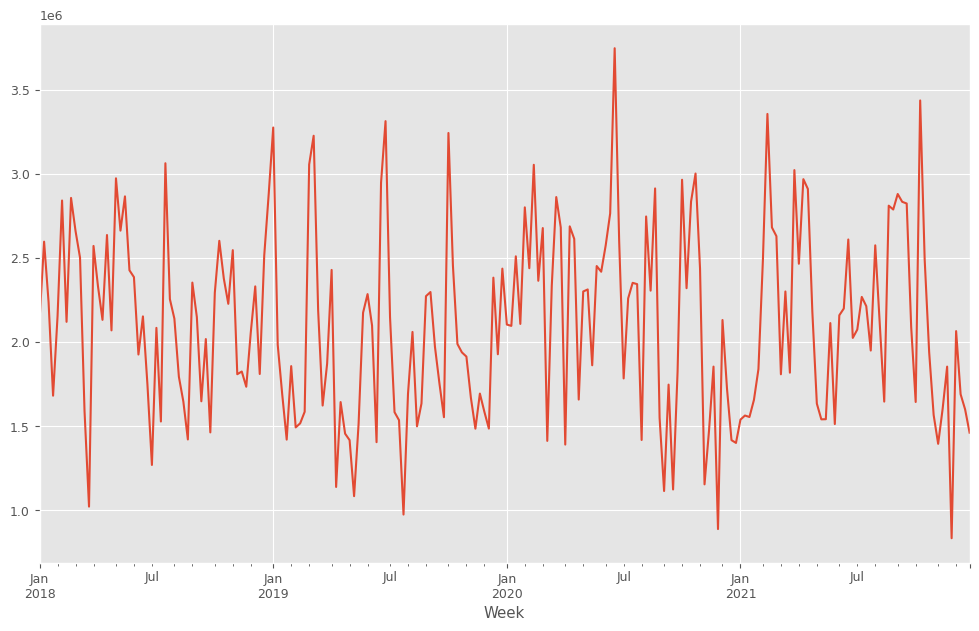
y.plot():y(目的変数)を折れ線グラフで表示します。plot()はPandasのデフォルトのグラフ化するためのプロット機能です。plt.show(): 作成されたグラフを画面に出力します。
説明変数X(各メディアのコスト)をまとめてプロットします。
以下、コードです。
X.plot(subplots=True) plt.show()
以下、実行結果です。
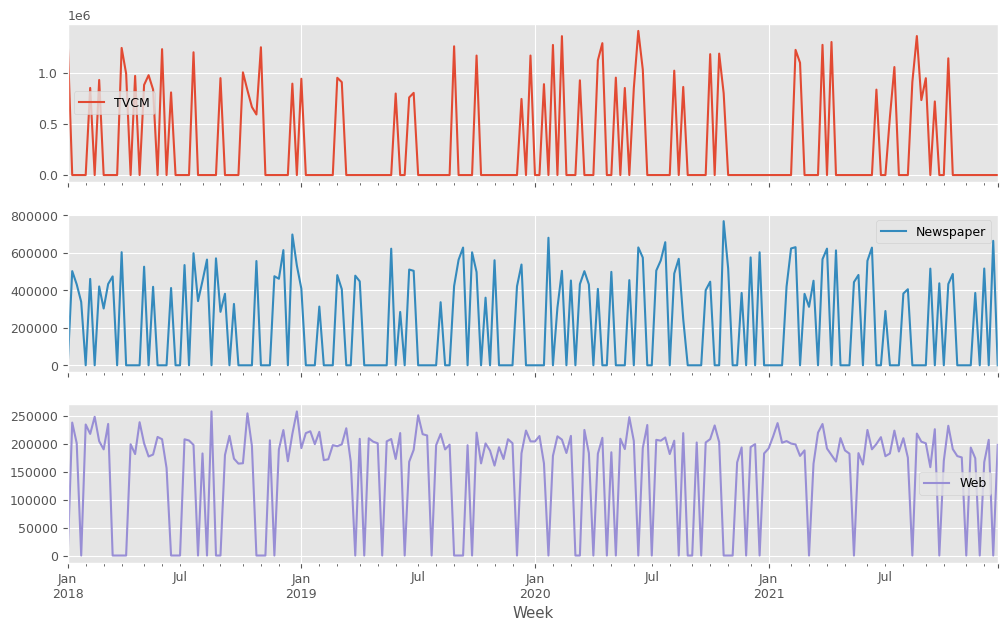
アドストック系の関数とクラス、そのグラフ化関数の定義
先ほどと重複しますが、アドストック系の関数である、シンプルなキャリーオーバー効果関数とそのクラス、シンプルな飽和関数とそのクラス、そしてそれらを視覚化(グラフ)する関数を作っていきます。
キャリオーバー効果関数
先ずは、シンプルなキャリーオーバー効果関数とそのクラスを作ります。
以下、コードです。
# キャリオーバー効果関数
def carryover_advanced(X: np.ndarray, length, peak, rate1, rate2, c1, c2):
X = np.append(np.zeros(length-1), X)
Ws = np.zeros(length)
for l in range(length):
if l<peak-1:
W = rate1**(abs(l-peak+1)**c1)
else:
W = rate2**(abs(l-peak+1)**c2)
Ws[length-1-l] = W
carryover_X = []
for i in range(length-1, len(X)):
X_array = X[i-length+1:i+1]
Xi = sum(X_array * Ws)/sum(Ws)
carryover_X.append(Xi)
return np.array(carryover_X)
# キャリオーバー効果を適用するカスタム変換器クラス
class CustomCarryOverTransformer(BaseEstimator, TransformerMixin):
def __init__(self, carryover_params=None):
self.carryover_params = carryover_params if carryover_params is not None else []
def fit(self, X, y=None):
return self
def transform(self, X):
if isinstance(X, pd.DataFrame):
X = X.to_numpy()
transformed_X = np.copy(X)
for i, params in enumerate(self.carryover_params):
transformed_X[:, i] = carryover_advanced(X[:, i], **params)
return transformed_X
飽和関数
次に、シンプルな飽和関数とそのクラスを作ります。
以下、コードです。
# 飽和関数(指数型)
def exponential_function(x, d):
result = 1 - np.exp(-d * x)
return result
# 飽和関数(ロジスティック曲線)
def logistic_function(x, L, k, x0):
result = L / (1+ np.exp(-k*(x-x0)))
return result
# 飽和関数を適用するカスタム変換器クラス
class CustomSaturationTransformer(BaseEstimator, TransformerMixin):
def __init__(self, curve_params=None):
self.curve_params = curve_params if curve_params is not None else []
def fit(self, X, y=None):
return self
def transform(self, X):
if isinstance(X, pd.DataFrame):
X = X.to_numpy()
transformed_X = np.copy(X)
for i, params in enumerate(self.curve_params):
saturation_function = params.pop('saturation_function')
if saturation_function == 'logistic':
transformed_X[:, i] = logistic_function(X[:, i], **params)
elif saturation_function == 'exponential':
transformed_X[:, i] = exponential_function(X[:, i], **params)
params['saturation_function'] = saturation_function # Returning the saturation_function back to params
return transformed_X
アドストック視覚化(グラフ)関数
どのようなアドストックになっているのかを視覚的に理解するために、視覚化(グラフ)する関数を作ります。
以下、コードです。
def plot_carryover_effect(params, feature_name, fig, axes, i):
max_length = max(10, params['length'])
x = np.concatenate(([1], np.zeros(max_length - 1)))
y = carryover_advanced(x, **params)
y = y / max(y) # Fixed line: y normalization moved here
axes[2*i].bar(np.arange(1, max_length + 1), y)
axes[2*i].set_title(f'Carryover Effect for {feature_name}')
axes[2*i].text(0, 1.1, params, ha='left',va='top')
axes[2*i].set_xlabel('Time Lag')
axes[2*i].set_ylabel('Effect')
axes[2*i].set_xticks(range(len(y)))
axes[2*i].set_ylim(0, 1.1)
def plot_saturation_curve(params, feature_name, fig, axes, i):
x = np.linspace(-1, 3, 400)
saturation_function = params.pop('saturation_function')
if saturation_function == 'logistic':
y = logistic_function(x, **params)
elif saturation_function == 'exponential':
y = exponential_function(x, **params)
axes[2*i+1].plot(x, y, label=feature_name)
axes[2*i+1].set_title(f'Saturation Curve for {feature_name}')
params['saturation_function'] = saturation_function
axes[2*i+1].text(-1, max(y)* 1.1, params, ha='left',va='top')
axes[2*i+1].set_xlabel('X')
axes[2*i+1].set_ylabel('Transformation')
axes[2*i+1].set_ylim(0, max(y) * 1.1)
axes[2*i+1].set_xlim(-1, 3)
def plot_effects(carryover_params, curve_params, feature_names):
fig, axes = plt.subplots(len(feature_names) * 2, 1, figsize=(12, 10*len(feature_names)))
for i, params in enumerate(carryover_params):
plot_carryover_effect(params, feature_names[i], fig, axes, i)
for i, params in enumerate(curve_params):
plot_saturation_curve(params, feature_names[i], fig, axes, i)
plt.tight_layout()
plt.show()
この関数を利用してみます。
先ず、キャリーオーバー効果関数と飽和関数のハイパーパラメータを設定します。このハイパーパラメータを、今作った視覚化(グラフ)する関数にインプットしグラフを描きます。特徴量名は何を設定しても問題ございません。
以下、コードです。
# キャリーオーバー効果関数のハイパーパラメータの設定
carryover_params = [
{'length': 10, 'peak': 2, 'rate1': 0.5, 'rate2': 0.8, 'c1': 2, 'c2': 1.5},
{'length': 5, 'peak': 1, 'rate1': 0.8, 'rate2': 0.5, 'c1': 1, 'c2': 1}
]
# 飽和関数のハイパーパラメータの設定
curve_params = [
{'saturation_function': 'logistic', 'L': 1, 'k': 5, 'x0': 0.5},
{'saturation_function': 'exponential', 'd': 5}
]
# 特徴量名の設定
feature_names = ['x1', 'x2']
# グラフで確認
plot_effects(carryover_params, curve_params, feature_names)
以下、実行結果です。
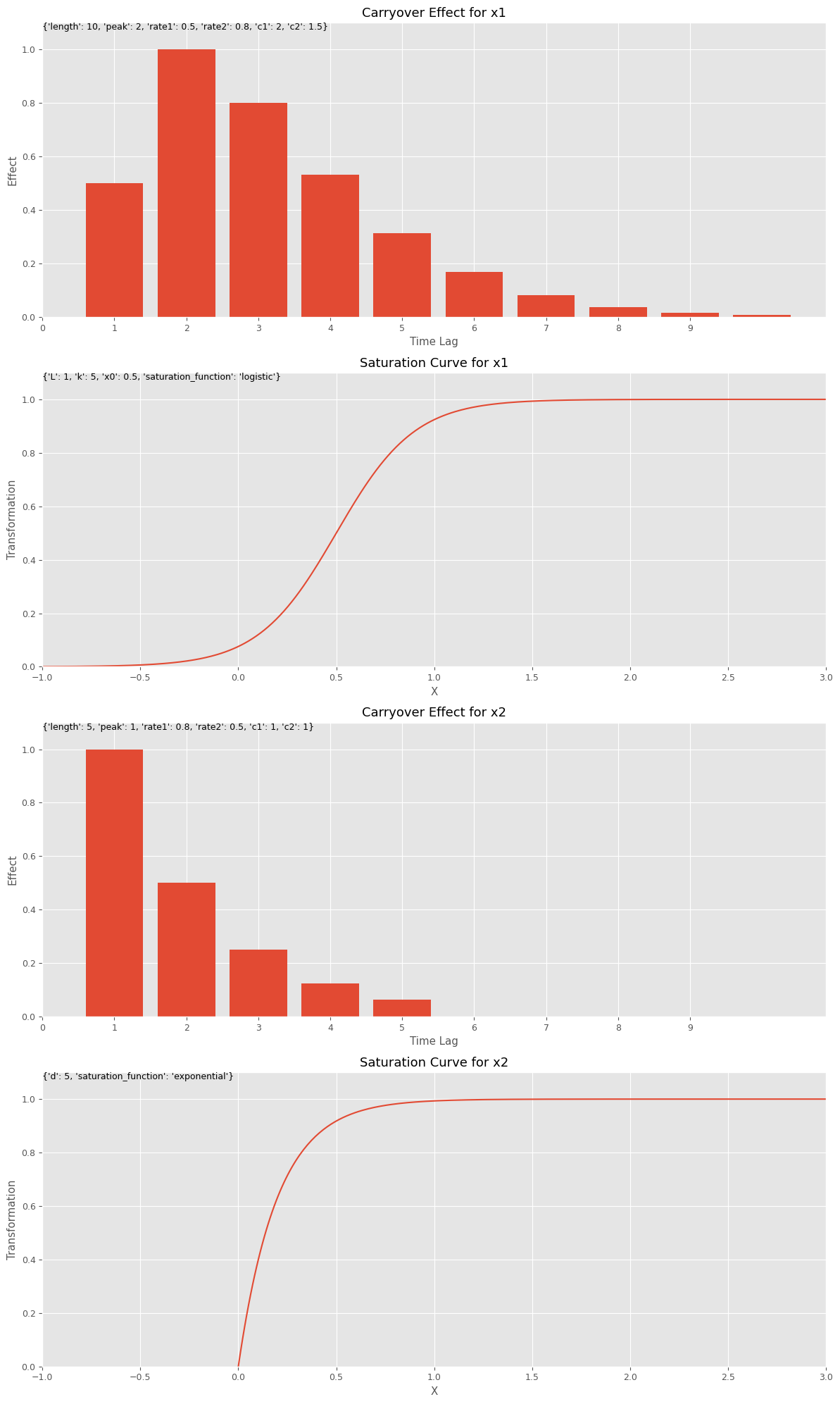
MMMパイプライン構築(ハイパーパラメータ自動調整)
ハイパーパラメータ自動調整
ハイパーパラメータを自動チューニングするため、Optunaの目的関数を定義します。
以下、コードです。
def objective(trial, X, y):
carryover_params = []
curve_params = []
n_features = X.shape[1]
# 特徴量の数だけ繰り返す(特徴量ごとに設定)
for i in X.columns:
# キャリオーバー効果パラメータの設定
carryover_length = trial.suggest_int(f'carryover_length_{i}', 1, 10)
carryover_peak = trial.suggest_int(f'carryover_peak_{i}', 1, carryover_length)
carryover_rate1 = trial.suggest_float(f'carryover_rate1_{i}', 0, 1)
carryover_rate2 = trial.suggest_float(f'carryover_rate2_{i}', 0, 1)
carryover_c1 = trial.suggest_float(f'carryover_c1_{i}', 0, 2)
carryover_c2 = trial.suggest_float(f'carryover_c2_{i}', 0, 2)
carryover_params.append({
'length': carryover_length,
'peak': carryover_peak,
'rate1': carryover_rate1,
'rate2': carryover_rate2,
'c1': carryover_c1,
'c2': carryover_c2,
})
# 飽和効果パラメータの設定
saturation_function = trial.suggest_categorical(f'saturation_function_{i}', ['logistic', 'exponential'])
if saturation_function == 'logistic':
curve_param_L = trial.suggest_float(f'curve_param_L_{i}', 0, 10)
curve_param_k = trial.suggest_float(f'curve_param_k_{i}', 0, 10)
curve_param_x0 = trial.suggest_float(f'curve_param_x0_{i}', 0, 2)
curve_params.append({
'saturation_function': saturation_function,
'L': curve_param_L,
'k': curve_param_k,
'x0': curve_param_x0,
})
elif saturation_function == 'exponential':
curve_param_d = trial.suggest_float(f'curve_param_d_{i}', 0, 10)
curve_params.append({
'saturation_function': saturation_function,
'd': curve_param_d,
})
# リッジ回帰の正則化パラメータの設定
alpha = trial.suggest_float('alpha', 1e-3, 1e+3)
# パイプラインの構築
pipeline = Pipeline(steps=[
('scaler', MinMaxScaler()),
('carryover', CustomCarryOverTransformer(carryover_params=carryover_params)),
('saturation', CustomSaturationTransformer(curve_params=curve_params)),
('ridge', Ridge(alpha=alpha))
])
# クロスバリデーションの実施
tscv = TimeSeriesSplit(n_splits=5)
scores = cross_val_score(pipeline, X, y, cv=tscv, scoring='neg_mean_squared_error')
rmse = np.mean([np.sqrt(-score) for score in scores])
# 戻り値
return rmse
このコードは、機械学習モデルのハイパーパラメータ最適化に使用される関数objectiveを定義しています。
以下、関数objectiveの概要です。
- キャリオーバー効果パラメータの設定
- 各特徴量に対して、キャリオーバー効果のパラメータ(効果の長さ、ピーク、減衰率1と2、および形状パラメータc1とc2)を選択します。
- 飽和効果パラメータの設定
- 各特徴量に対して、飽和効果の種類(ロジスティック関数または指数関数)を選択し、それぞれのパラメータ(ロジスティック関数の場合はL、k、x0、指数関数の場合はd)を選択します。
- リッジ回帰の正則化パラメータの設定
- モデルの正則化パラメータ
alphaを選択します。
- モデルの正則化パラメータ
- パイプラインの構築
MinMaxScaler、CustomCarryOverTransformer、CustomSaturationTransformer、およびRidge回帰を含むパイプラインを作成します。
- クロスバリデーションの実施
TimeSeriesSplitを使用して時系列データを分割し、パイプラインの性能を評価します。- ここで、ネガティブ平均二乗誤差をスコアリングメトリクスとして使用し、その平方根を取ることでRMSEを計算します。
- 戻り値
- 計算されたRMSEの平均値を返却します。Optunaはこの値を最小化するようにパラメータを調整します。
この目的関数は、モデルの予測性能を最適化するためのパラメータを自動的に見つけ出すために設計されています。
時系列データの特性を考慮した特徴量エンジニアリング(キャリオーバー効果と飽和効果)を組み込むことで、モデルがデータの動的な挙動をより正確に捉えられるようになります。さらに、リッジ回帰の正則化を適切に設定することで、過学習を防ぎつつ、汎化性能の高いモデルを構築することが可能になります。
目的関数を最適化し、最適なハイパーパラメータを探索します。
以下、コードです。
# Optunaのスタディの作成と最適化の実行
study = optuna.create_study(direction='minimize')
objective_with_data = partial(objective, X=X, y=y)
study.optimize(objective_with_data, n_trials=10000)
print("Best trial:")
trial = study.best_trial
print(f"Value: {trial.value}")
print("Params: ")
for key, value in trial.params.items():
print(f"{key}: {value}")
以下、実行結果です。
Best trial: Value: 170439.1852778197 Params: carryover_length_<span>TVCM</span>: 5 carryover_peak<span>_TVCM</span>: 1 carryover_rate1<span>_TVCM</span>: 0.3058696390391196 carryover_rate2<span>_TVCM</span>: 0.48496086171569186 carryover_c1<span>_TVCM</span>: 0.9911677783216924 carryover_c2<span>_TVCM</span>: 0.9707002410934593 saturation_function<span>_TVCM</span>: exponential curve_param_d<span>_TVCM</span>: 1.279937918050393 carryover_length<span>_Newspaper</span>: 2 carryover_peak<span>_Newspaper</span>: 1 carryover_rate1<span>_Newspaper</span>: 0.964132471218172 carryover_rate2<span>_Newspaper</span>: 0.2891985228708162 carryover_c1<span>_Newspaper</span>: 1.9654104022957872 carryover_c2<span>_Newspaper</span>: 0.15686241834634368 saturation_function<span>_Newspaper</span>: logistic curve_param_L<span>_Newspaper</span>: 3.764758681853768 curve_param_k<span>_Newspaper</span>: 0.4933020850524151 curve_param_x0<span>_Newspaper</span>: 1.1886209326094748 carryover_length<span>_Web</span>: 1 carryover_peak<span>_Web</span>: 1 carryover_rate1<span>_Web</span>: 0.7832256824629069 carryover_rate2<span>_Web</span>: 0.399101594968567 carryover_c1<span>_Web</span>: 0.6700060521324637 carryover_c2<span>_Web</span>: 1.4960935801007993 saturation_function<span>_Web</span>: exponential curve_param_d<span>_Web</span>: 1.1658893777812827 alpha: 0.0014479555667443952
最適なハイパーパラメータを使いMMMを構築するため、ハイパーパラメータの値を抽出し、以下のリストなどを作成します。
best_carryover_params:キャリーオーバー効果関数のハイパーパラメータのリストbest_curve_params:飽和関数のハイパーパラメータのリストbest_alpha:Ridge回帰の正則化パラメータ
先ず、そのための関数を定義します。
以下、コードです。
# 関数で最適ハイパーパラメータを取得してリストを返す
def get_optimal_hyperparameters(trial):
carryover_keys = ['length', 'peak', 'rate1', 'rate2', 'c1', 'c2']
curve_keys_logistic = ['L', 'k', 'x0']
curve_keys_exponential = ['d']
n_features = X.shape[1]
# ハイパーパラメータを抽出しキーと値の辞書を作成
def fetch_params(prefix, index, params, trial_params):
return {key: trial_params[f'{prefix}_{key}_{index}'] for key in params}
# キャリーオーバー効果関数ハイパーパラメータを抽出
carryover_params = [fetch_params('carryover', i, carryover_keys, trial.params) for i in X.columns]
# 飽和関数ハイパーパラメータを抽出
curve_params = []
for i in X.columns:
saturation_function = trial.params[f'saturation_function_{i}']
curve_param = {'saturation_function': saturation_function}
if saturation_function == 'logistic':
curve_param.update(fetch_params('curve_param', i, curve_keys_logistic, trial.params))
elif saturation_function == 'exponential':
curve_param.update(fetch_params('curve_param', i, curve_keys_exponential, trial.params))
curve_params.append(curve_param)
# 推定器ハイパーパラメータを抽出
alpha = trial.params['alpha']
return carryover_params, curve_params, alpha
この関数get_optimal_hyperparametersは、Optunaの最適化プロセスを通じて見つかった最適なハイパーパラメータを整理し、それらを構造化された形式(リストなど)で返します。
関数の中を、簡単に説明します。
- キャリオーバー効果パラメータの抽出
carryover_keysリストに定義されたキー(length,peak,rate1,rate2,c1,c2)を使用して、各特徴量に対するキャリオーバー効果に関連するハイパーパラメータを取得します。fetch_params関数を使用して、Optunaの試行からこれらのパラメータ値を取り出し、辞書形式で整理します。
- 飽和関数パラメータの抽出
- 各特徴量に対して、
saturation_function(飽和関数のタイプ)を決定します。これはlogisticかexponentialのいずれかです。 - 飽和関数のタイプに応じて、適切なパラメータ(ロジスティック関数の場合は
L,k,x0、指数関数の場合はd)を取得します。 - 同様に、
fetch_params関数を使用して、これらのパラメータ値を取り出し、辞書形式で整理します。
- 各特徴量に対して、
- リッジ回帰の正則化パラメータの抽出
- Optunaの試行から
alphaパラメータを取得します。
- Optunaの試行から
- 返り値
- キャリオーバー効果に関連するハイパーパラメータのリスト
carryover_params - 飽和関数に関連するハイパーパラメータのリスト
curve_params - リッジ回帰モデルの正則化パラメータ
alpha
- キャリオーバー効果に関連するハイパーパラメータのリスト
この関数を使い、ハイパーパラメータの値を抽出しリストとして出力します。
以下、コードです。
# ハイパーパーパラメータ抽出 best_carryover_params, best_curve_params, best_alpha = get_optimal_hyperparameters(study.best_trial)
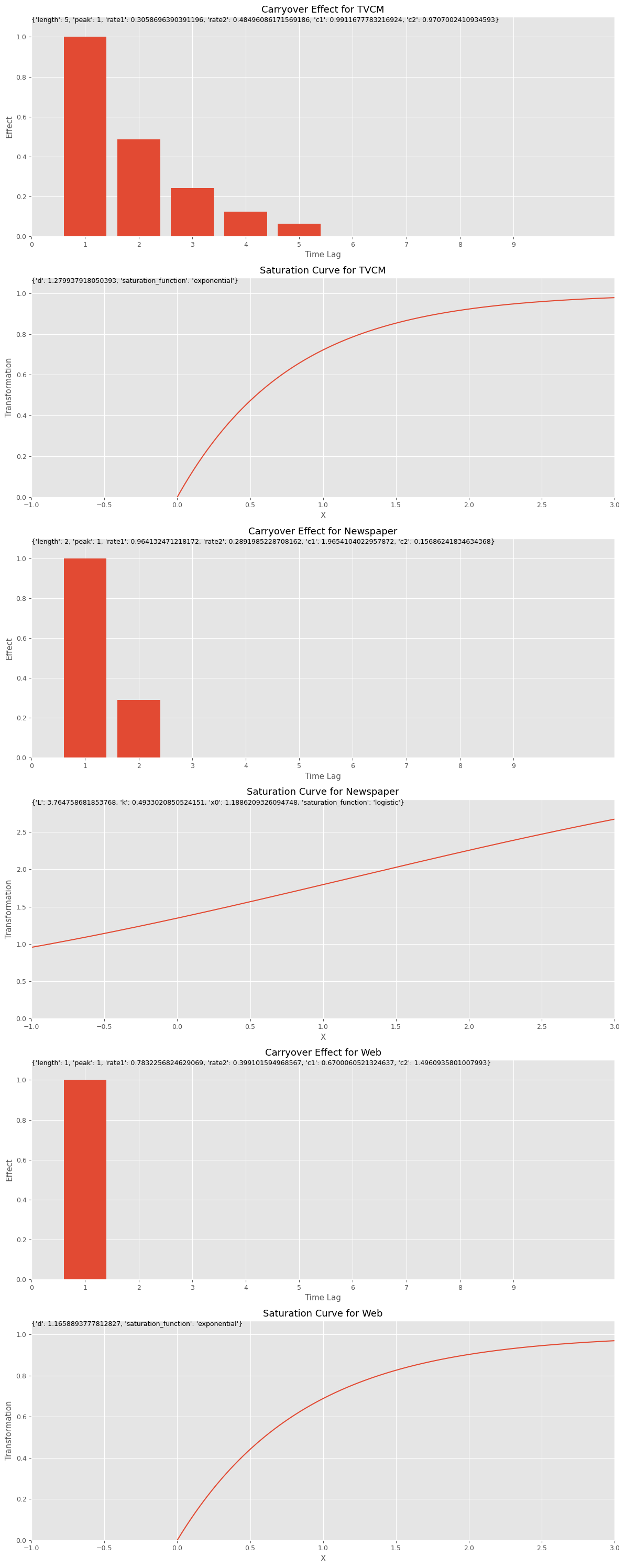
キャリーオーバー効果関数のハイパーパラメータのリストであるbest_carryover_paramsと、飽和関数のハイパーパラメータのリストであるbest_curve_paramsから、どのようなアドストック(キャリーオーバー効果関数と飽和関数)になったのかをグラフで確認してみます。
以下、コードです。
# グラフで確認 plot_effects(best_carryover_params, best_curve_params, X.columns)
以下、実行結果です。
MMM構築
このハイパーパラメータでMMMパイプラインを構築していきます。
以下、コードです。
# 最適なパイプラインの構築
MMM_pipeline = Pipeline(steps=[
('scaler', MinMaxScaler()),
('carryover', CustomCarryOverTransformer(carryover_params=best_carryover_params)),
('saturation', CustomSaturationTransformer(curve_params=best_curve_params)),
('ridge', Ridge(alpha=best_alpha))
])
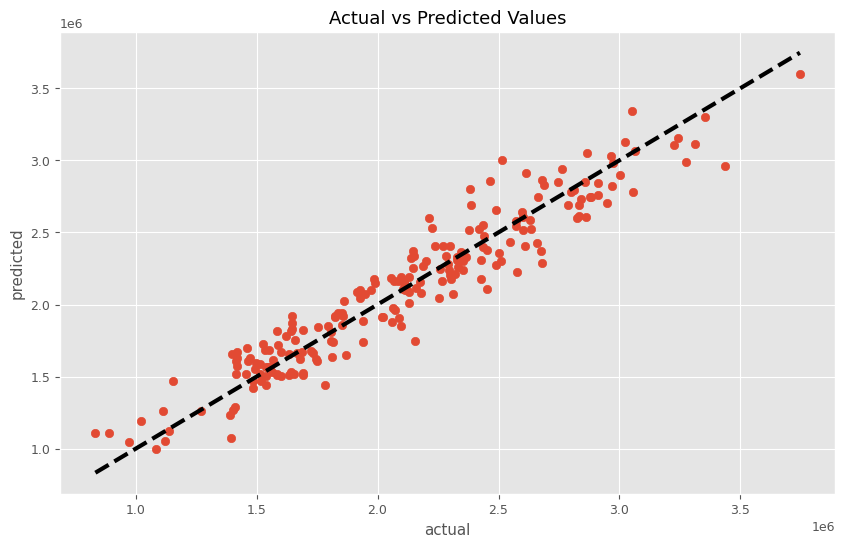
このMMMパイプラインを学習し、実測と予測の散布図を描いてみます。
以下、コードです。
# パイプラインを使って学習
MMM_pipeline.fit(X, y)
# 学習したモデルを使って予測
predictions = MMM_pipeline.predict(X)
# 予測結果の表示
plt.figure(figsize=(10, 6))
plt.scatter(y, predictions)
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=3)
plt.xlabel('actual')
plt.ylabel('predicted')
plt.title('Actual vs Predicted Values')
plt.show()
以下、実行結果です。
前々回作った以下の関数群を使い、MMMモデル構築から貢献度算出、マーケティングROIの計算をしていきます。
- MMM構築
train_and_evaluate_model:MMMの構築plot_actual_vs_predicted:構築したMMMの予測値の時系列推移
- 後処理(結果の出力)
calculate_and_plot_contribution:売上貢献度の算出(時系列推移)summarize_and_plot_contribution:売上貢献度構成比の算出calculate_marketing_roi:マーケティングROIの算出
繰り返しの説明になります。
以下からダウンロードできます。
mmm_functions.py ※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/oi17
mmm_functions.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。
以下のコードで呼び出せます。
from mmm_functions import *
上手くいかないときは、mmm_functions.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。
関数train_and_evaluate_modelを使い、MMMを評価します。
以下、コードです。
# MMMの構築 trained_model, pred = train_and_evaluate_model(MMM_pipeline, X, y)
以下、実行結果です。
RMSE: 164833.0016554395 MAE: 132411.15415897832 MAPE: 0.06688402717908698 R2: 0.9128397875306006
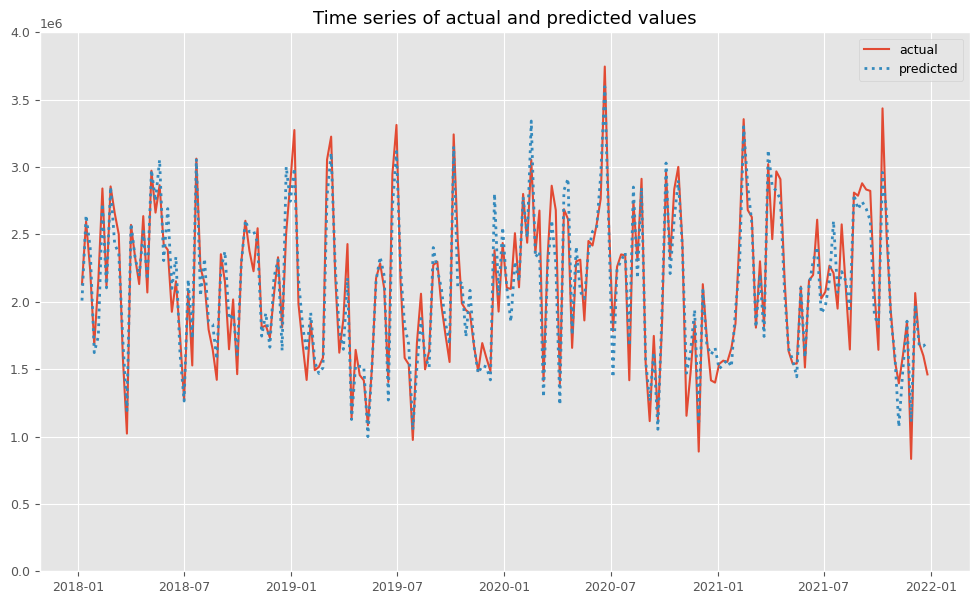
関数plot_actual_vs_predictedを使い、関数train_and_evaluate_modelで構築したMMMの予測値と実測値をプロットします。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 4e6))
以下、実行結果です。
後処理(結果の出力)
MMMを構築したら、貢献度やマーケティングROIなどを計算していきます。
先ずは、貢献度を計算します。
以下、コードです。
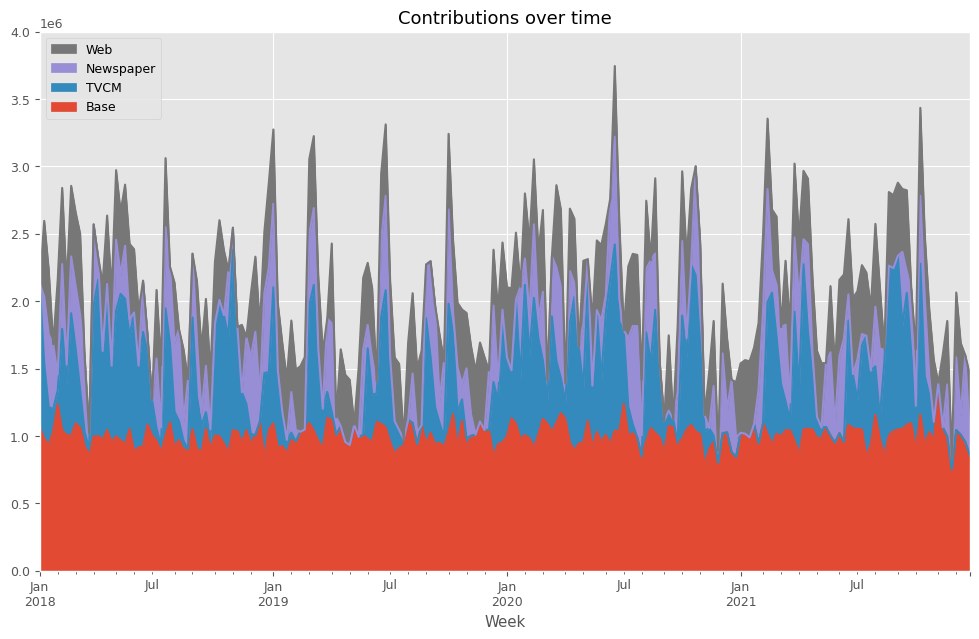
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 4e6))
以下、実行結果です。
Base TVCM Newspaper Web Week 2018-01-07 1.060201e+06 1.071799e+06 0.000000 0.000000 2018-01-14 9.815916e+05 5.580466e+05 495445.483949 561016.386398 2018-01-21 9.298335e+05 2.838515e+05 541002.159069 481512.807331 2018-01-28 1.035116e+06 1.653971e+05 480387.005819 0.000000 2018-02-04 1.234821e+06 1.021115e+05 118393.486033 700074.034556 ... ... ... ... ... 2021-11-28 7.515644e+05 0.000000e+00 82335.593959 0.000000 2021-12-05 1.043330e+06 0.000000e+00 541442.101120 479928.253036 2021-12-12 1.009185e+06 0.000000e+00 148247.812718 532066.714729 2021-12-19 9.565957e+05 0.000000e+00 643004.258865 0.000000 2021-12-26 8.582062e+05 0.000000e+00 162578.876379 440314.929153 [208 rows x 4 columns]
次に、貢献度の割合を計算します。
以下、コードです。
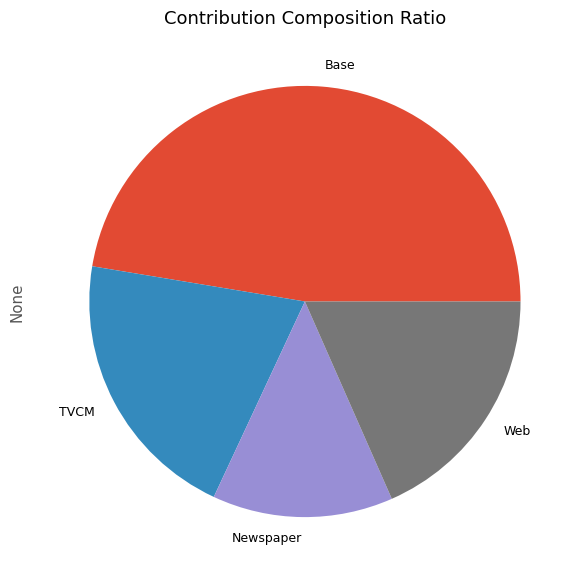
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution)
以下、実行結果です。
contribution ratio Base 2.078153e+08 0.473862 TVCM 9.064921e+07 0.206699 Newspaper 5.941148e+07 0.135471 Web 8.068015e+07 0.183968
最後に、各メディアのマーケティングROIを計算します。
以下、コードです。
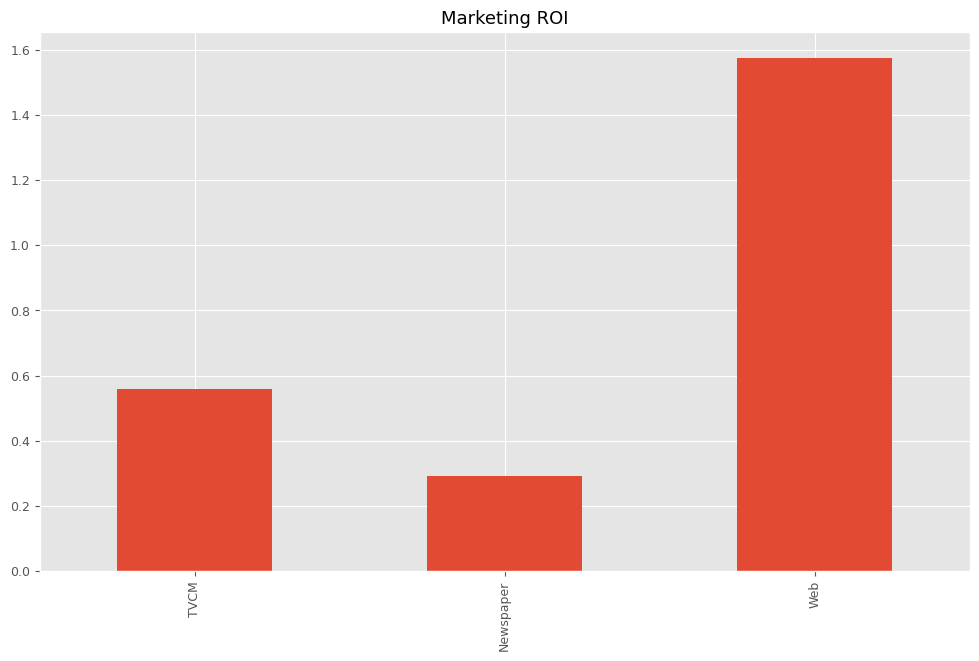
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution)
以下、実行結果です。
TVCM 0.558953 Newspaper 0.291942 Web 1.575230 dtype: float64
より発展させたい方へ
実は、他の飽和関数を含め3つにしても、4つにしてもても構いません。そこから最適なものを自動選択できるようにすればいいだけです。
代表的なところですと、例えば、シグモイド (S字曲線)系ですと……
- ロジスティック関数 ※今回利用
- 双曲線正接関数 (tanh)
- アークタンジェント関数
- ゴンペルツ関数
- ヒル関数
- ワイブル関数
- チャップマン関数
- ボルツマン関数
……などです。
もしろん、キャリーオーバー効果も1つではなく、2つにしても、3つにしても構いません。そこから最適なものを自動選択できるようにすればいいだけです。
代表的なところですと、例えば……
- 指数減衰モデル (Exponential Decay Model) ※最もシンプル
- 幾何減衰モデル (Geometric Decay Model) ※今回利用(減衰率一定)
- 分布遅延モデル (Distributed Lag Model) ※幾何減衰モデルの減衰率が一定ではない
- 多項式減衰モデル (Polynomial Decay Model) ※分布遅延モデルの多項式化
……などです。
興味のある方は、色々な飽和関数やキャリーオーバー効果関数をPython上で定義し、各クラスに追加し遊んでみてください。
まとめ
今回は、アドストックの飽和関数を自動選択し構築するMMMというお話しをしました。
具体的には、飽和関数(指数型)と飽和関数(ロジスティック型)のどちらかを自動選択できるように、アドストックのハイパーパラメータに、飽和関数の選択も含めました。
興味のある方は、色々な飽和関数やキャリーオーバー効果関数をPython上で定義し、各クラスに追加し遊んでみてください。
ただ、これだけだと変換器の自動選択・調整だけになってしまいます。
そこで次回は、ここに推定器の自動選択を含めたいと思います。
要するに、推定器自動選択を含めたMMMハイパーパラメータ自動調整です。
次回は単に、今回のコードに線形系の回帰モデル(一般的な線形回帰やRidge回帰、PLS回帰など)の自動選択を含めるだけです。
PythonによるMMM(マーケティングミックスモデリング)とビジネス活用- 振返り分析・線形回帰系モデル編(その5)-アドストック線形回帰系MMM(推定器自動選択)

