- 問題
- 答え
- 解説
Python コード:
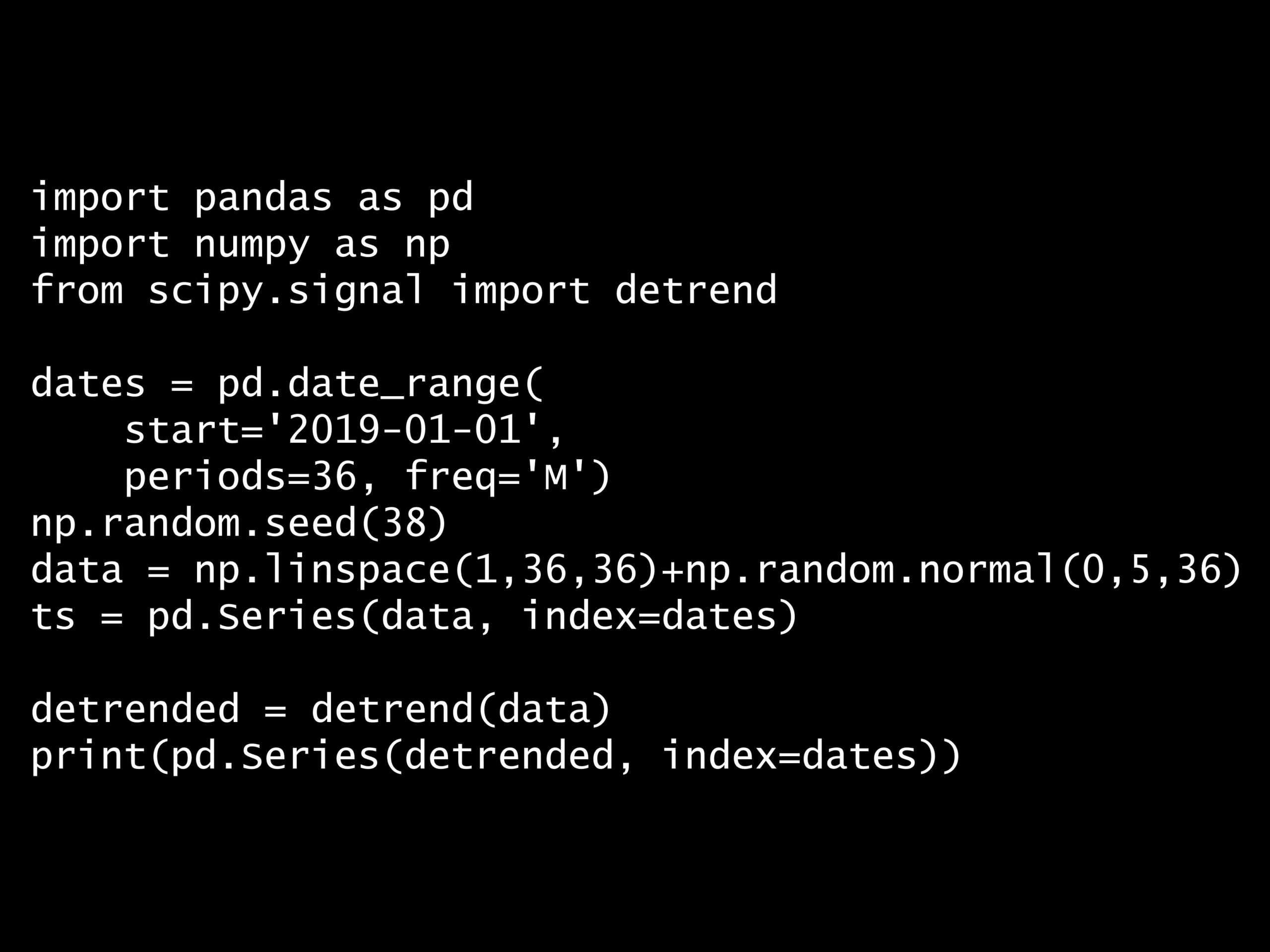
import pandas as pd
import numpy as np
from scipy.signal import detrend
dates = pd.date_range(
start='2019-01-01',
periods=36, freq='M')
np.random.seed(38)
data = np.linspace(1,36,36)+np.random.normal(0,5,36)
ts = pd.Series(data, index=dates)
detrended = detrend(data)
print(pd.Series(detrended, index=dates))
回答の選択肢:
(A) データのトレンド成分
(B) データの季節成分
(C) トレンド除去後の値
(D) トレンド成分と季節成分を除去した値
2019-01-31 3.524179 2019-02-28 -3.126401 2019-03-31 -0.863487 2019-04-30 -0.094790 2019-05-31 4.958568 2019-06-30 6.649957 2019-07-31 -3.813912 2019-08-31 -7.706396 2019-09-30 -2.752956 2019-10-31 -2.180017 2019-11-30 -3.834613 2019-12-31 -9.967262 2020-01-31 4.092844 2020-02-29 -1.658455 2020-03-31 11.310263 2020-04-30 4.657336 2020-05-31 8.313065 2020-06-30 -2.859799 2020-07-31 5.239384 2020-08-31 -1.257936 2020-09-30 1.084059 2020-10-31 -10.673638 2020-11-30 0.737457 2020-12-31 -0.612747 2021-01-31 -1.544773 2021-02-28 0.825589 2021-03-31 1.935144 2021-04-30 2.947404 2021-05-31 -0.330066 2021-06-30 2.225624 2021-07-31 -4.620637 2021-08-31 -5.013140 2021-09-30 6.651136 2021-10-31 -4.228006 2021-11-30 9.304012 2021-12-31 -7.316988 Freq: M, dtype: float64
正解: (C)
回答の選択肢:
(A) データのトレンド成分
(B) データの季節成分
(C) トレンド除去後の値
(D) トレンド成分と季節成分を除去した値
- コードの説明
-
このPythonコードは、時系列データからトレンドを除去するためのものです。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterimport pandas as pdimport numpy as npfrom scipy.signal import detrenddates = pd.date_range(start='2019-01-01',periods=36, freq='M')np.random.seed(38)data = np.linspace(1,36,36)+np.random.normal(0,5,36)ts = pd.Series(data, index=dates)detrended = detrend(data)print(pd.Series(detrended, index=dates))import pandas as pd import numpy as np from scipy.signal import detrend dates = pd.date_range( start='2019-01-01', periods=36, freq='M') np.random.seed(38) data = np.linspace(1,36,36)+np.random.normal(0,5,36) ts = pd.Series(data, index=dates) detrended = detrend(data) print(pd.Series(detrended, index=dates))
import pandas as pd import numpy as np from scipy.signal import detrend dates = pd.date_range( start='2019-01-01', periods=36, freq='M') np.random.seed(38) data = np.linspace(1,36,36)+np.random.normal(0,5,36) ts = pd.Series(data, index=dates) detrended = detrend(data) print(pd.Series(detrended, index=dates))詳しく説明します。
月ごとの日付を生成します。ここでは2019年1月開始で36個の月ごとの日付を生成しています。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterdates = pd.date_range(start='2019-01-01', periods=36, freq='M')dates = pd.date_range(start='2019-01-01', periods=36, freq='M')dates = pd.date_range(start='2019-01-01', periods=36, freq='M')
datesに格納されているデータは次のようになっています。DatetimeIndex(['2019-01-31', '2019-02-28', '2019-03-31', '2019-04-30', '2019-05-31', '2019-06-30', '2019-07-31', '2019-08-31', '2019-09-30', '2019-10-31', '2019-11-30', '2019-12-31', '2020-01-31', '2020-02-29', '2020-03-31', '2020-04-30', '2020-05-31', '2020-06-30', '2020-07-31', '2020-08-31', '2020-09-30', '2020-10-31', '2020-11-30', '2020-12-31', '2021-01-31', '2021-02-28', '2021-03-31', '2021-04-30', '2021-05-31', '2021-06-30', '2021-07-31', '2021-08-31', '2021-09-30', '2021-10-31', '2021-11-30', '2021-12-31'], dtype='datetime64[ns]', freq='M')トレンド(等間隔に増加する数列)とノイズ(正規分布に従うランダムな数)を組み合わせたデータ列を生成します。ノイズは
numpyの乱数生成器を使っています。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighternp.random.seed(38)data = np.linspace(1,36,36)+np.random.normal(0,5,36)np.random.seed(38) data = np.linspace(1,36,36)+np.random.normal(0,5,36)np.random.seed(38) data = np.linspace(1,36,36)+np.random.normal(0,5,36)
dataに格納されているデータは次のようになっています。[ 6.04352824 0.38438324 3.63873208 5.39886456 11.44365789 14.12648157 4.65404799 1.7529985 7.69787381 9.26224799 8.59908687 3.45787341 18.50941468 13.74955062 27.70970327 22.04821172 26.69537597 16.51394652 25.60456515 20.09867955 23.43211026 12.66584759 25.06837813 24.70960894 24.76901822 28.13081531 30.23180534 32.23550009 29.94946598 33.49659086 27.64176456 28.2406974 40.89640846 31.00870084 45.53215379 29.90258888]
日付(インデックス)
datesとデータ(値)dataから構成されるpandasのSeriesオブジェクトを作ります。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighternp.random.seed(38)data = np.linspace(1,36,36)+np.random.normal(0,5,36)np.random.seed(38) data = np.linspace(1,36,36)+np.random.normal(0,5,36)np.random.seed(38) data = np.linspace(1,36,36)+np.random.normal(0,5,36)
tsに格納されているデータは次のようになっています。2019-01-31 6.043528 2019-02-28 0.384383 2019-03-31 3.638732 2019-04-30 5.398865 2019-05-31 11.443658 2019-06-30 14.126482 2019-07-31 4.654048 2019-08-31 1.752998 2019-09-30 7.697874 2019-10-31 9.262248 2019-11-30 8.599087 2019-12-31 3.457873 2020-01-31 18.509415 2020-02-29 13.749551 2020-03-31 27.709703 2020-04-30 22.048212 2020-05-31 26.695376 2020-06-30 16.513947 2020-07-31 25.604565 2020-08-31 20.098680 2020-09-30 23.432110 2020-10-31 12.665848 2020-11-30 25.068378 2020-12-31 24.709609 2021-01-31 24.769018 2021-02-28 28.130815 2021-03-31 30.231805 2021-04-30 32.235500 2021-05-31 29.949466 2021-06-30 33.496591 2021-07-31 27.641765 2021-08-31 28.240697 2021-09-30 40.896408 2021-10-31 31.008701 2021-11-30 45.532154 2021-12-31 29.902589 Freq: M, dtype: float64
scipyのdetrend関数を使って、データから現行のトレンド(等間隔に増加する数列)を除去します。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterdetrended = detrend(data)detrended = detrend(data)detrended = detrend(data)
detrendedをpandas Series形式に変換し出力します。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterprint(pd.Series(detrended, index=dates))print(pd.Series(detrended, index=dates))print(pd.Series(detrended, index=dates))
2019-01-31 3.524179 2019-02-28 -3.126401 2019-03-31 -0.863487 2019-04-30 -0.094790 2019-05-31 4.958568 2019-06-30 6.649957 2019-07-31 -3.813912 2019-08-31 -7.706396 2019-09-30 -2.752956 2019-10-31 -2.180017 2019-11-30 -3.834613 2019-12-31 -9.967262 2020-01-31 4.092844 2020-02-29 -1.658455 2020-03-31 11.310263 2020-04-30 4.657336 2020-05-31 8.313065 2020-06-30 -2.859799 2020-07-31 5.239384 2020-08-31 -1.257936 2020-09-30 1.084059 2020-10-31 -10.673638 2020-11-30 0.737457 2020-12-31 -0.612747 2021-01-31 -1.544773 2021-02-28 0.825589 2021-03-31 1.935144 2021-04-30 2.947404 2021-05-31 -0.330066 2021-06-30 2.225624 2021-07-31 -4.620637 2021-08-31 -5.013140 2021-09-30 6.651136 2021-10-31 -4.228006 2021-11-30 9.304012 2021-12-31 -7.316988 Freq: M, dtype: float64
- 時系列データからトレンド成分を除去する方法
-
時系列データからトレンド成分を除去する方法はいくつかあります。ここでは、主に使われる方法をいくつか紹介します。
- 移動平均法(Moving Average)
- 差分法(Differencing)
- 季節調整とトレンド除去(Seasonal and Trend decomposition using Loess, STL)
- 回帰分析(Regression)
- HPフィルター(Hodrick-Prescott Filter)
scipyライブラリのdetrend関数は、回帰分析(Regression)による方法でトレンド成分を除去します。それぞれの方法について簡単に説明し、最後に
scipyライブラリのdetrend関数による方法にも簡単に触れます。Contents [hide]
移動平均法
移動平均法(Moving Average)は、時系列データ分析における基本的な手法の一つで、データの平滑化(スムージング)やトレンド成分の除去に用いられます。
この方法の目的は、時系列データ内の短期的な変動やノイズを減らし、データの基本的な動きやトレンドを明確にすることです。
移動平均法の種類
移動平均法には、主に以下の二つのタイプがあります。
- 単純移動平均(Simple Moving Average, SMA): これは、時系列データの各点について、その点とその周囲の点(前後の点を含む)の算術平均を計算する方法です。例えば、7日間の単純移動平均を求める場合、各点についてその日を含む前後3日間(合計7日間)のデータ点の平均を計算します。
- 指数移動平均(Exponential Moving Average, EMA): この方法では、最近のデータにより大きな重みを付け、過去に遡るにつれてその重みを指数的に減少させます。これにより、最新のトレンドや変動に対してより敏感な平滑化が可能となります。
移動平均法の実施手順
- 窓幅(window)の選択: 移動平均を計算する際には、どれだけの期間(窓幅)を平均化するかを決める必要があります。窓幅が大きいほど、平滑化の度合いは高くなりますが、データの細かい変動は失われやすくなります。
- 平均計算: 選択した窓幅に基づいて、各データ点についてその点とその周囲の点の平均を計算します。単純移動平均の場合、すべての点に同じ重みが与えられます。指数移動平均の場合、最新のデータにより大きな重みが与えられます。
- トレンド除去: 計算した移動平均を元のデータから引くことで、トレンド成分を除去します。この操作により、データから線形トレンドや緩やかなトレンド成分が取り除かれ、周期的な変動やランダムな変動がより明確に観察できるようになります。
移動平均法の利用
移動平均法は、金融市場の分析(株価や為替レートのトレンド分析)、気象データの分析、製造業における品質管理など、多岐にわたる分野で応用されています。
特に、短期的な変動や季節性の影響を除去し、長期的なトレンドやパターンを把握したい場合に有効です。また、移動平均線のクロスオーバーは、トレーディング戦略において重要なシグナルとして用いられることもあります。
差分法
差分法(Differencing)は、時系列データ分析における基本的な手法の一つで、データのトレンド成分を除去するために用いられます。
この方法は特に、データに含まれる線形トレンドや非線形トレンドを取り除くのに効果的です。差分法を用いることで、データの定常性を高め、時系列分析や予測モデル構築に適した形にデータを変換することができます。
差分法の基本
差分法では、時系列データの隣接する観測値間の差(差分)を計算します。具体的には、時刻
この一次差分は、時刻
差分法の応用
一次差分: 最も基本的な差分で、直前の観測値との差を取ります。線形トレンドに対して効果的です。
二次差分: 一次差分の差分を取ることで、より高度な非線形トレンドを除去することができます。具体的には、一次差分の結果に対して再度差分を取ります。
季節差分: 季節性を持つデータに対して行う差分で、例えば月次データの場合は12のラグを持つ差分を計算します。これにより、季節性の影響を除去することができます。
差分法の利点と制限
利点:
- 線形トレンドやある程度の非線形トレンドを簡単に除去できる。
- データの定常性を向上させ、時系列分析や予測モデル構築に適した形にすることができる。
制限:
- 差分を取ることでデータの情報が失われる可能性がある。
- 高次の差分を用いると、データのノイズが強調されることがある。
- 季節差分を適切に選択するには、データの季節性のパターンを理解している必要があります。
差分法は、ARIMA(自己回帰和分移動平均モデル)などの時系列予測モデルにおいて、データを定常化するための前処理ステップとして広く用いられています。また、トレンド成分の除去後に残るデータのパターンや周期性を分析することで、より深い洞察を得ることが可能になります。
季節調整とトレンド除去
季節調整とトレンド除去における「Seasonal and Trend decomposition using Loess (STL)」は、時系列データをトレンド成分、季節成分、そして残差成分に分解する強力な手法です。
この方法は、非常に柔軟性が高く、さまざまな種類の季節性パターンやトレンド変動に適応することができます。STLはロバストな局所回帰技術(LoessまたはLowessとも呼ばれる)を使用しており、その柔軟性と効果性から、実際のビジネスデータ分析において広く利用されています。
主な特徴
柔軟性: STLは、季節成分とトレンド成分の変動幅が時間とともに変化するデータに対しても、良好に機能します。また、季節パターンの周期が一定でない場合にも対応可能です。
ロバスト性: 外れ値や異常値の影響を受けにくい設計となっており、実際のビジネスデータによく見られる突発的な変動や非定型的なデータポイントを効果的に処理できます。
分解能: STLは時系列データを三つの明確な成分に分解します:トレンド成分(データの長期的な変化を示す)、季節成分(定期的なパターンや周期性を示す)、残差成分(トレンドや季節性によって説明されないデータの変動)。この分解により、データの背後にある構造をより明確に理解することができます。
STLのプロセス
- 季節成分の抽出: データから季節性パターンを識別し、抽出します。これは、データセット全体にわたる季節的な変動の平均を計算することで行われます。
- トレンド成分の抽出: 季節調整されたデータからトレンド成分を抽出します。これは、ロバストな局所回帰技術を使用して行われ、データの長期的な変化を捉えます。
- 残差成分の計算: 季節成分とトレンド成分をデータから除去した後に残る成分です。これは、トレンドや季節性によって説明されないデータの変動を示します。
STLの利用
STLは、経済データ、販売データ、交通データなど、季節性やトレンドが重要な役割を果たすあらゆる時系列データの分析に適しています。季節調整されたデータやトレンド調整されたデータを分析することで、データの背後にある真の動きやパターンをより明確に理解することができ、将来のトレンド予測や意思決定プロセスをサポートします。
STL分解は、時系列分析のための強力なツールであり、データの季節性とトレンドの両方を明確に分離することで、より深い洞察を提供し、より正確な予測を可能にします。
回帰分析
回帰分析は、統計学における強力なツールであり、特に時系列データのトレンド成分をモデル化し分析するのに有効です。
時系列データに対して回帰分析を適用することで、データの背後にあるトレンドを数学的に定式化し、そのトレンドを明確に理解することが可能になります。
このプロセスは、トレンドの推定と除去の両方を行うことができ、データの周期的な変動やランダムな変動に焦点を当てるための前処理ステップとしても役立ちます。
トレンドのモデル化
時系列データのトレンドをモデル化するために、時間を独立変数として、時系列データの観測値を従属変数とする回帰モデルを構築します。トレンドの形状に応じて、以下のような異なる回帰モデルが使用されます。
線形トレンド: 最も基本的な形式で、データが時間に対して直線的に増加または減少すると仮定します。モデルは
多項式トレンド: データがより複雑な曲線的なトレンドを示す場合、2次、3次、あるいはそれ以上の多項式を用いてモデル化することができます。例えば、2次の場合は
トレンドの推定と除去
回帰分析を用いてトレンド成分を推定した後、その推定されたトレンドを元の時系列データから引くことで、トレンドを除去することができます。
これにより、トレンドの影響を受けないデータを得ることが可能となり、データの周期的な変動やランダムな変動をより詳細に分析することができます。
回帰分析の利用
回帰分析を利用することで、以下のような分析が可能になります。
- トレンドの方向性と強度の定量的な評価
- データのトレンドからの偏差を示す残差の分析
- トレンドを考慮した上での将来のデータポイントの予測
回帰分析は、経済データ、販売データ、気象データなど、様々な時系列データに適用可能であり、ビジネスや科学研究における意思決定支援に貢献します。特に、データに含まれるトレンドを正確に理解し、除去することで、より純粋なデータ分析や予測モデリングを行うことができます。
HPフィルター
HPフィルター(Hodrick-Prescott Filter)は、時系列データ分析においてトレンド成分と周期成分を分離するために広く用いられる手法です。
特に経済学の分野で好んで使用され、マクロ経済学的な時系列データ(例えば、GDP、失業率など)のトレンドを抽出するのに効果的です。
このフィルターは、時系列データ内の長期的な動向を反映する滑らかなトレンド線を生成し、それによってデータの周期的な変動を明らかにします。
基本原理
HPフィルターの基本的な考え方は、時系列データをトレンド成分と周期成分の二つに分解することです。この分解は、以下の最適化問題を解くことによって実行されます。
ここで、
この最適化問題の第一項は、実際のデータとトレンド成分との二乗誤差の合計を最小化することを目的としています。第二項は、トレンド成分の二次差分の二乗和を最小化することで、トレンドの滑らかさを確保するためのペナルティ項です。パラメータ
HPフィルターの使用
HPフィルターは、特に経済時系列の分析において、景気循環の分析や経済成長のトレンドを把握する際に有効です。
例えば、経済成長率の時間的変動を分析する際に、HPフィルターを使用して長期的な成長トレンドを抽出し、その上で短期的な景気の変動を調査することができます。
利点と制限
利点: HPフィルターは、トレンドと周期成分を直感的に分離できるため、経済データの長期的な動向と短期的な変動を分析するのに非常に便利です。
制限: HPフィルターの主な批判点は、平滑化パラメータ
HPフィルターは、その直感的なアプローチと実装の容易さから、経済学をはじめとする多くの分野で広く用いられていますが、その適用に際しては、データの特性や分析の目的を考慮し、パラメータの選択に注意を払う必要があります。
scipyライブラリのdetrend関数scipyライブラリのdetrend関数は、時系列データや信号から線形トレンドを除去するために用いられます。この関数は、基本的にデータに対して線形回帰を行い、得られた線形トレンドをデータから引くことでトレンド成分を除去します。
具体的な手順は以下の通りです。
- データに対して線形モデル(
- 次に、この線形モデルによって予測される値(つまり、トレンド成分)を元のデータから引きます。この操作によって、データから線形トレンドが除去されます。
- 結果として、トレンド成分が取り除かれたデータが得られます。このデータは、もとの時系列データの周期的またはランダムな変動をより明確に表すことができるようになります。
scipy.signal.detrend関数は、特に時系列分析や信号処理で用いられるデータの前処理ステップとして便利です。この関数を使うことで、データから線形トレンドを簡単に除去し、データの他の特性(例えば、周期性やノイズ)に焦点を当てることが可能になります。この処理は、特に周期性の分析やノイズフィルタリングを行う前の準備として重要です。