データを活用したマーケティング戦略は、ビジネスの成功に不可欠です。その中心に位置するのが、マーケティングミックスモデリング(MMM)です。
マーケティングミックスモデリング(MMM)は、過去のデータを分析する「振り返り分析」と未来のトレンドを予測する「近未来分析」の両方で有効に活用される強力なツールです。
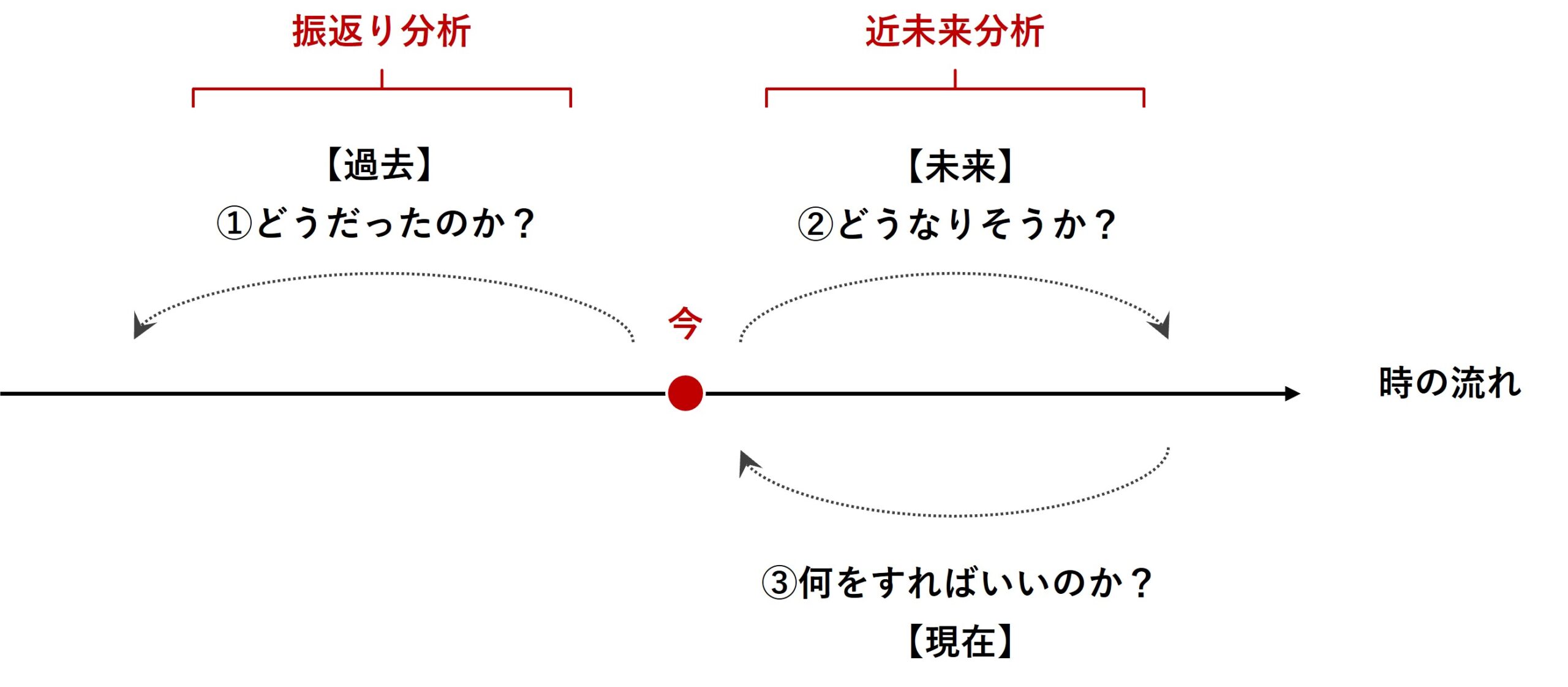
振返り分析のためのMMMは、各広告・販促の手段が、どのくらいの売上などに貢献し、それが効率的だったのかどうかを、明らかにすることでした。
さらに一歩先に話しを進め、どの広告・販促の手段に、どの程度のコストをかけて投資をするのが効率的なのか? を明らかにする振返り分析もあります。
要するに、広告・販促の手段にかけるコストの最適投資配分です。
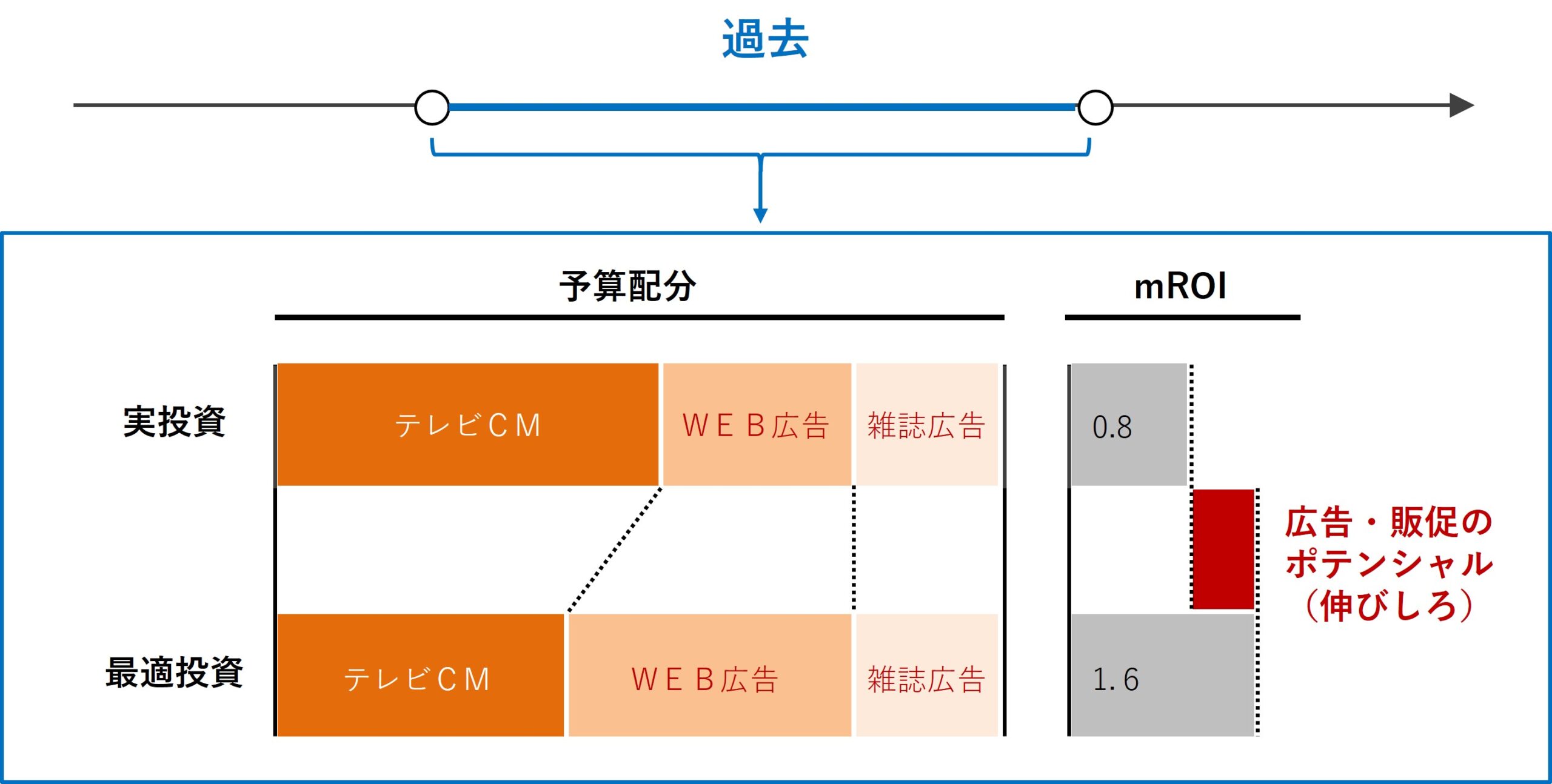
色々なアプローチがありますが、ストレートなのは非線形計画問題(非線形最適化)を定式化しソルバーで解くことです。具体的に言うと、PythonのScyPyである程度は実現することができます。
非線形計画問題などの数理最適化に関しては、以下で言及していますので、興味ある方は見ていただければと思います。
今回は、以下のRidge回帰ベースのアドストック付きMMM(Ridge MMMパイプライン)で、最適投資配分を求めていきます。
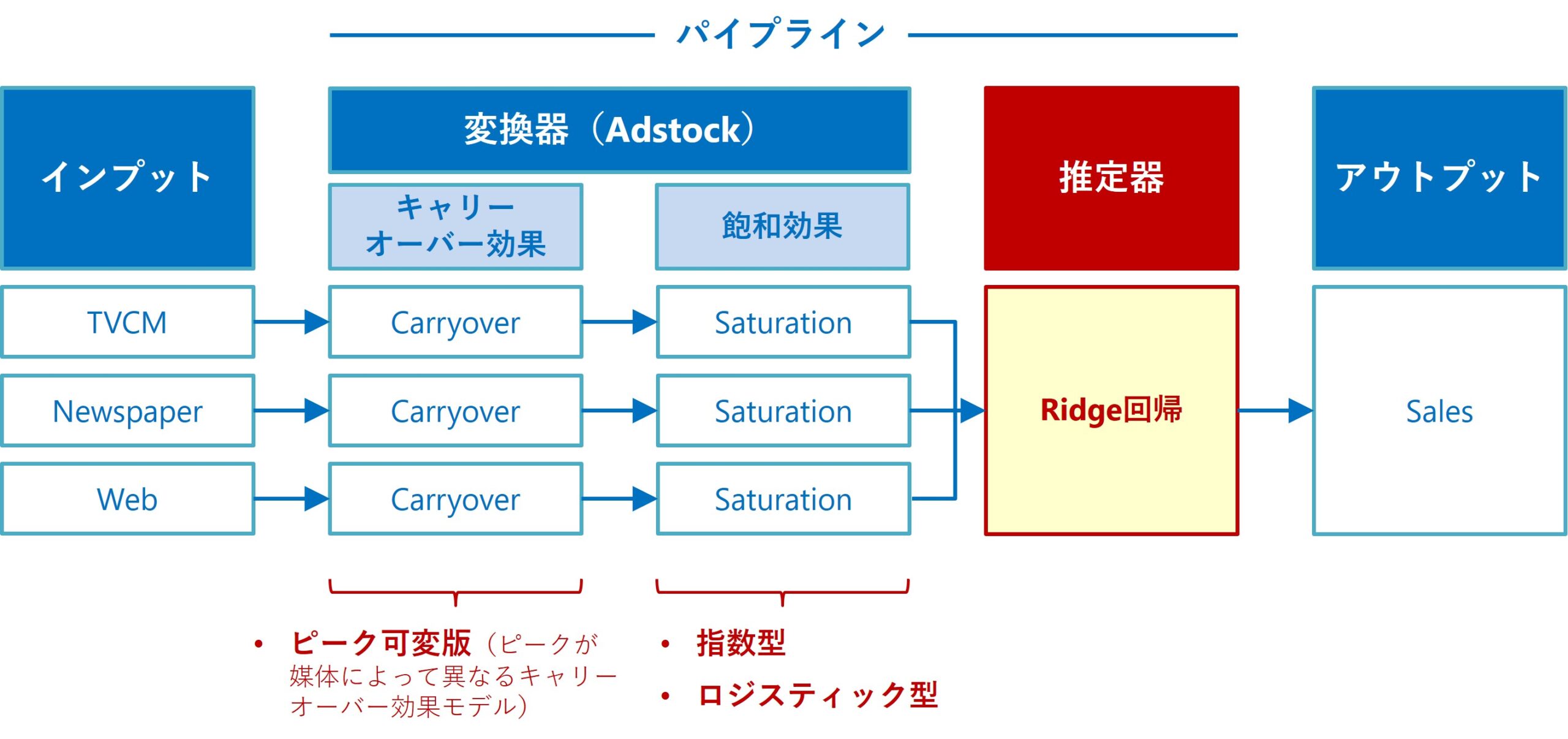
このRidge MMMパイプラインを、より知りたい方は以下の記事を読んでください。
PythonによるMMM(マーケティングミックスモデリング)とビジネス活用- 振返り分析・線形回帰系モデル編(その4)-アドストック線形回帰系MMM(飽和関数自動選択)
今回は、上記で利用した関数などをまとめた、Pythonファイルを使っていきます。
以下からダウンロードできます。
mmm_functions5.py ※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/uno8
mmm_functions5.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。
以下のコードで呼び出せます。
from mmm_functions5 import *
上手くいかないときは、mmm_functions5.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。
Contents
予算最適化問題の定式化
数理最適化は、ある制約条件のもとで、目的関数を最大化(もしくは最小化)する問題です。
数理最適化には、線形計画問題や非線形計画問題、混合整数計画問題などがあります。
MMM(マーケティングミックスモデリング)の予算最適化問題は、非線形計画問題として定式化することが多いです。
例えば、最適化する目的関数としてMMMそのものを設定し、制約条件としてコスト制約(全体のコストが決められている負のコストはない、など)を設定したりします。
その場合、全体コスト一定の下で売上を最大化する、広告・販促の手段に対するコストの最適配分を求める問題になります。

ちなみに、モデル構築で登場する目的変数と、数理最適化の目的関数は別物ですので、ご注意ください。
先ほどの例ですと、MMMそのものが目的関数、MMMの出力である売上が目的変数になります。
MMMのメジャーの最適化問題には、もう1つあります。
売上を落とさずに全体コストを最小化する問題です。
そのような、広告・販促の手段に対するコストの最適配分を求める問題もあります。

まとめると、メジャーなMMMの最適化問題は以下の2パターンです。
- 全体コスト一定の下で売上を最大化する、広告・販促の最適配分を求める問題
- 売上一定の下で全体コストを最小化する、広告・販促の最適配分を求める問題
今回は、「全体コスト一定の下で売上を最大化する、広告・販促の最適配分を求める問題」で行きます。
準備
モジュールの読み込み
先ず、必要なモジュールを読み込みます。
以下、コードです。
from mmm_functions5 import *
先ほども説明しましたが、再度説明します。
Pythonファイル(mmm_functions5.py)そのものは、以下からダウンロードできます。
mmm_functions5.py ※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/uno8
mmm_functions5.pyには、MMMで共通して利用する処理を関数化したものや、クラス、モジュール類などを記載しています。
mmm_functions5.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。
以下のコードで呼び出せます。
from mmm_functions5 import *
データセットの読み込み
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/4zdt'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
このデータセットの以下のデータセットを前提に説明します。
- y:目的変数 – 売上金額(Sales)
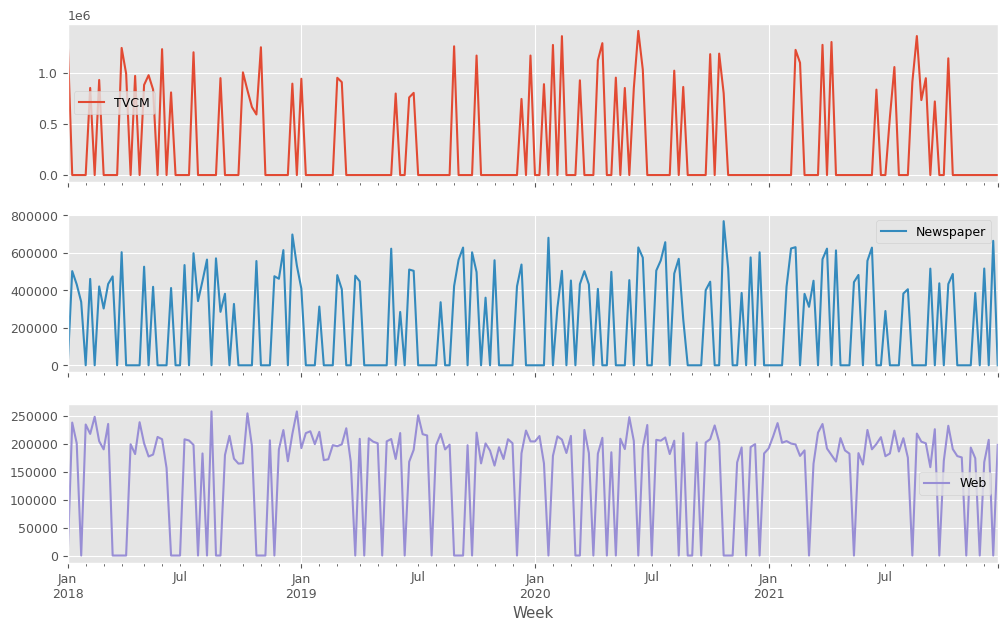
- X:特徴量(説明変数)- TVCM、Newspaper、Webのコスト
目的変数y(売上)をプロットします。
以下、コードです。
y.plot() plt.show()
以下、実行結果です。
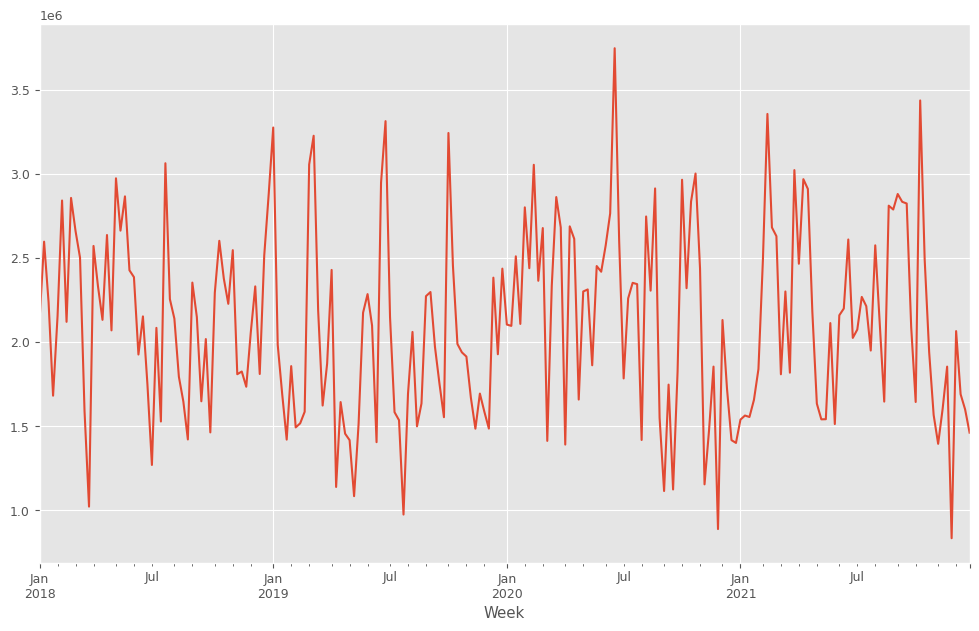
y.plot():y(目的変数)を折れ線グラフで表示します。plot()はPandasのデフォルトのグラフ化するためのプロット機能です。plt.show(): 作成されたグラフを画面に出力します。
説明変数X(各メディアのコスト)をまとめてプロットします。
以下、コードです。
X.plot(subplots=True) plt.show()
以下、実行結果です。
目的関数作り
今回の最適投資配分問題の目的関数は、Ridge MMMMパイプラインそのものになります。

OptunaでRidge MMMMパイプラインの最適なハイプ―パラメータを探索し、そのハイパーパラメータを使い構築&学習します。
最適なハイパーパラメータの探索
Ridge MMMパイプラインの最適なハイパーパラメータの探索をします。
以下、コードです。
# Optunaのスタディの作成と最適化の実行
study = optuna.create_study(direction='minimize')
objective_with_data = partial(ridge_objective, X=X, y=y)
study.optimize(objective_with_data, n_trials=10000, show_progress_bar=True)
print("Best trial:")
trial = study.best_trial
print(f"Value: {trial.value}")
print("Params: ")
for key, value in trial.params.items():
print(f"{key}: {value}")
以下、実行結果です。
Best trial: 9573. Best value: 86169.2: 100%|██████████| 10000/10000 [4:56:47<00:00, 1.78s/it]Best trial: Value: 86169.2253982674 Params: carryover_length_TVCM: 3 carryover_peak_TVCM: 2 carryover_rate1_TVCM: 0.999394872598024 carryover_rate2_TVCM: 0.09227343849257215 carryover_c1_TVCM: 1.5792733041946232 carryover_c2_TVCM: 1.438417229133962 saturation_function_TVCM: exponential curve_param_d_TVCM: 5.487040394160279 carryover_length_Newspaper: 2 carryover_peak_Newspaper: 1 carryover_rate1_Newspaper: 0.8159531072584766 carryover_rate2_Newspaper: 0.052935290552299286 carryover_c1_Newspaper: 0.4165107051515125 carryover_c2_Newspaper: 1.8855406581810146 saturation_function_Newspaper: exponential curve_param_d_Newspaper: 1.8816177530506872 carryover_length_Web: 1 carryover_peak_Web: 1 carryover_rate1_Web: 0.6214488386702899 carryover_rate2_Web: 0.3216984925931279 carryover_c1_Web: 0.2118410531764691 carryover_c2_Web: 1.8820013645044467 saturation_function_Web: exponential curve_param_d_Web: 6.782308480215278 alpha: 0.033769283029704444
探索し得られたハイパーパラメータを抽出します。
以下、コードです。
# ハイパーパーパラメータ抽出
best_carryover_params, best_curve_params, best_alpha = ridge_get_optimal_hyperparameters(
X.columns,
study.best_trial)
- best_carryover_params:キャリーオーバー効果関数のハイパーパラメータ
- best_curve_params:飽和関数のハイパーパラメータ
- best_alpha:Ridge回帰のハイパーパラメータ
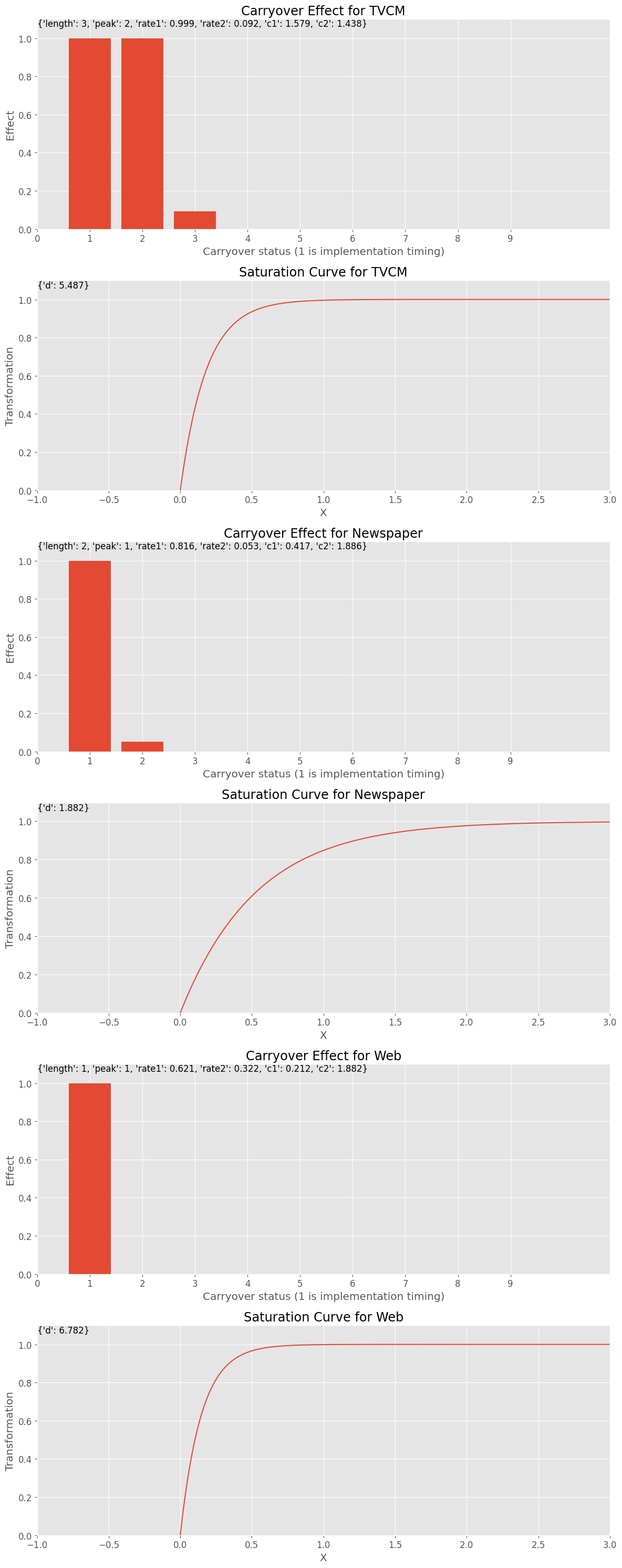
このハイパーパラメータで定義されるキャリーオーバー効果と飽和効果が、どういうものかを視覚的に見てみます。
以下、コードです。
# グラフで確認 plot_effects(best_carryover_params, best_curve_params, X.columns)
以下、実行結果です。
MMMパイプラインの構築
これらの最適なハイパーパラメータでMMMパイプラインを構築します。
以下、コードです。
# 最適なパイプラインの構築
MMM_pipeline = Pipeline(steps=[
('scaler', MinMaxScaler()),
('carryover', CustomCarryOverTransformer(carryover_params=best_carryover_params)),
('saturation', CustomSaturationTransformer(curve_params=best_curve_params)),
('estimator', Ridge(alpha=best_alpha))
])
このMMMパイプラインを学習します。
以下、コードです。
# パイプラインを使って学習 trained_model, pred = train_and_evaluate_model(MMM_pipeline, X, y)
以下、実行結果です。
RMSE: 83841.7135498238 MAE: 62032.898005372605 MAPE: 0.0300612256798814 R2: 0.9715326816442589
それぞれの指標を簡単に解釈していくと……
RMSE (Root Mean Squared Error): 83841.71
この値は平均二乗誤差の平方根を表しており、予測値と実際値の差の大きさを示します。値が小さいほど良いモデルということになります。
MAE (Mean Absolute Error): 62032.90
これは絶対誤差の平均値で、予測値と実際値の差の絶対値の平均を表します。値が小さいほど良いモデルです。
MAPE (Mean Absolute Percentage Error): 0.0301 (3.01%)
この指標はパーセンテージで表された絶対誤差の平均値です。100%に近づくほど予測精度が低くなります。
R2 (R-squared): 0.9715 (97.15%)
決定係数と呼ばれ、モデルの当てはまり具合を0から1の範囲で表します。1に近いほど当てはまりが良いことを意味します。
総合的に見ると、目的変数yが売上金額であると考えるとRMSEとMAEの値は大きすぎるとは言えず、MAPEが3%程度とかなり小さく、R2が97%と非常に高い値になっています。つまり、このモデルは全体として予測精度が高く、実際の値とよく一致していると判断できます。
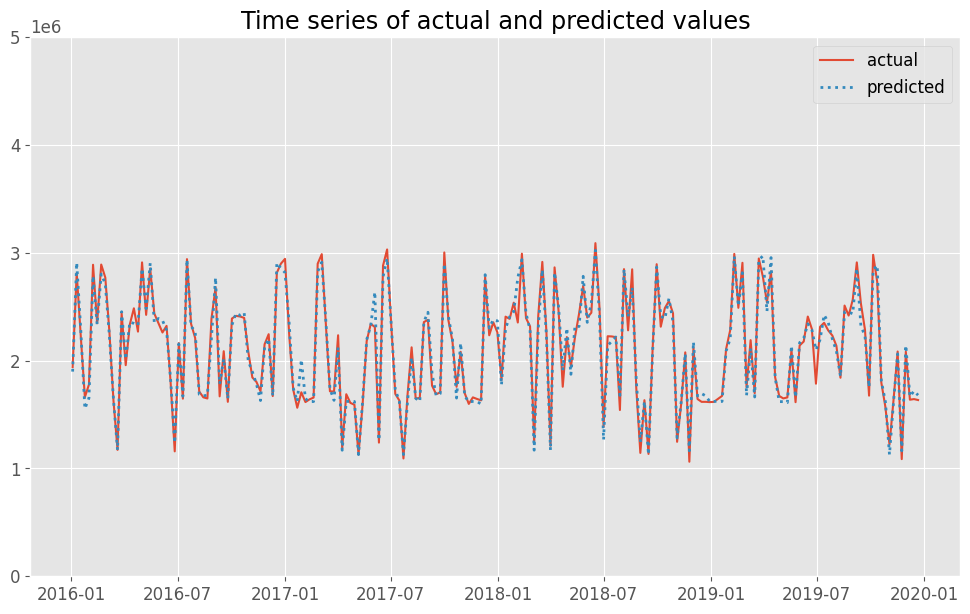
実測値と予測値の時系列推移を比較してみます。
以下、コードです。
# 実測値と予測値の時系列推移 plot_actual_vs_predicted(y.index, y.values, pred.y.values, (0, 5e6))
以下、実行結果です。actualが実測値で、predictedが予測値です。
学習済みモデルの保存と読み込み
必要があれば、学習済みのMMMパイプラインを外部ファイル(joblib形式)として保存しておくといいでしょう。
以下、コードです。
# 学習済みモデルtrained_modelを外部ファイルとして保存する model_path = 'ridgeMMM_trained_model.joblib' joblib.dump(trained_model, model_path)
joblib形式とは、scikit-learnの機械学習モデルやデータを保存するためのファイル形式のことです。
joblibを使うことで、学習済みモデルやデータを簡単にディスク上に保存/読み込みできます。
joblib形式のファイルには以下の利点があります。
- 高速シリアライズ/デシリアライズ:Python標準的な保存手段であるpickle形式よりも高速にシリアライズ(オブジェクトを保存をするためにバイト列に変換すること)できます。
- メモリ効率:joblibはメモリマップを使用するため、大規模なデータでもメモリ効率が良くなります。
- ランダムアクセス:joblibは入出力をバイト単位で処理できるので、特定の部分のみを読み込むランダムアクセスが可能です。
- 並列化:joblibは高度な並列化をサポートしているため、複数のCPUコアで並列に処理できます。
したがって、scikit-learnのモデルやデータをディスクに保存・読み込みする際は、joblib形式を利用することが一般的です。保存されたjoblibファイルから必要に応じてモデルやデータを復元することができます。
外部ファイル(joblib形式)として保存した学習済みのMMMパイプラインを読み込むとき、以下のコードで実施します。
以下、コードです。
# 外部ファイル(学習済みモデル)を読み込む model_path = 'ridgeMMM_trained_model.joblib' trained_model = joblib.load(model_path)
MMMパイプラインを得るのに、多大なる時間を消費することが多々あります。そのため、利用するMMMパイプラインは外部ファイルとして保存しておくことをお勧めします。
売上貢献度とマーケティングROI
このMMMパイプラインから、売上貢献度やマーケティングROIなどを求めていきます。
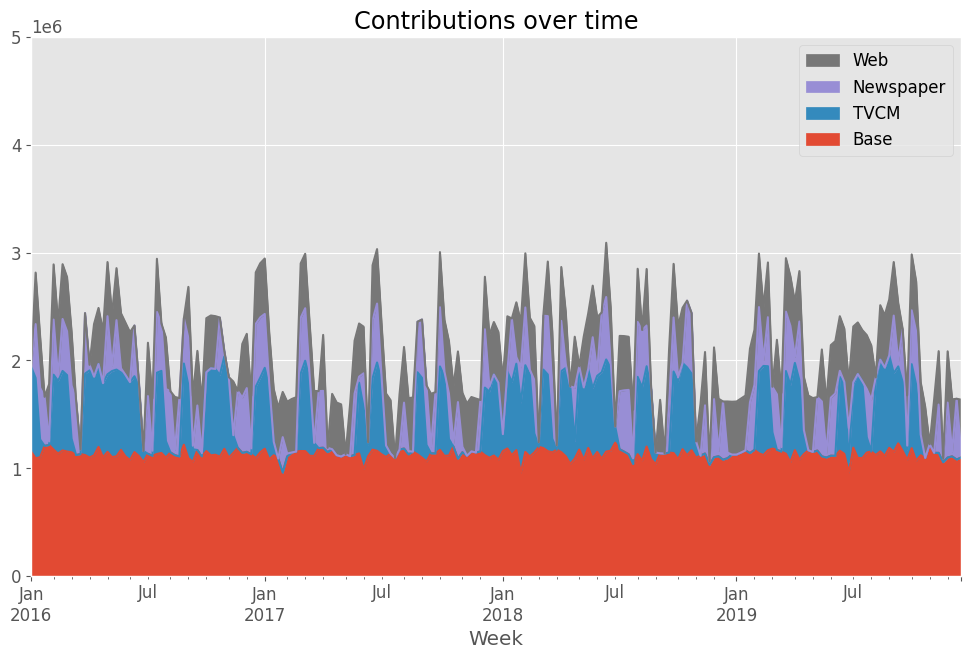
先ずは、貢献度の推移です。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 5e6)) print(contribution)
以下、実行結果です。
Base TVCM Newspaper Web Week 2016-01-03 1.153765e+06 786582.806062 0.000000 0.000000 2016-01-10 1.091884e+06 744500.213531 499690.004687 477766.726283 2016-01-17 1.100579e+06 165722.606634 479100.994561 480054.538237 2016-01-24 1.206391e+06 0.000000 455026.399407 0.000000 2016-01-31 1.214497e+06 0.000000 32868.842956 531321.798745 ... ... ... ... ... 2019-11-24 1.054343e+06 0.000000 32478.422969 0.000000 2019-12-01 1.098175e+06 0.000000 509725.183738 475503.781820 2019-12-08 1.108758e+06 0.000000 45322.640377 483981.857037 2019-12-15 1.079688e+06 0.000000 563911.592289 0.000000 2019-12-22 1.098651e+06 0.000000 57239.755864 479013.088702 [208 rows x 4 columns]
次に、貢献度の構成比を求めます。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution) print(contribution_results)
以下、実行結果です。
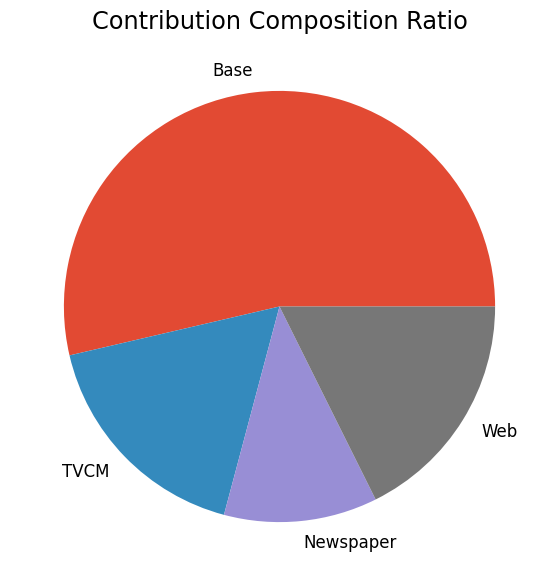
contribution ratio Base 2.348197e+08 0.536425 TVCM 7.533721e+07 0.172101 Newspaper 5.036019e+07 0.115044 Web 7.723204e+07 0.176430
売上貢献度とコストから、マーケティングROIを求めます。
以下、コードです。
# マーケティングROIの算出 ROI = calculate_marketing_roi(X, contribution) print(ROI)
以下、実行結果です。
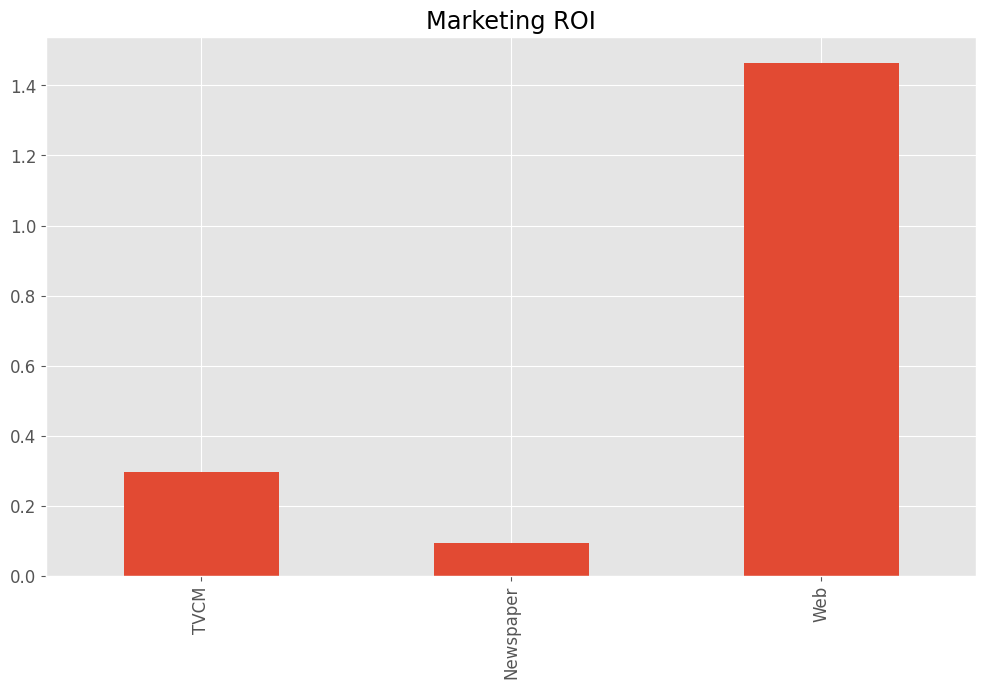
TVCM 0.295622 Newspaper 0.095115 Web 1.465170 dtype: float64
売上貢献度(横軸)×マーケティングROI(縦軸)のマップを描きます。円の大きさはコストを表します。
以下、コードです。
# 散布図作成(売上貢献度×マーケティングROI) data_to_plot = plot_scatter_of_contribution_and_roi(X, contribution) print(data_to_plot)
以下、実行結果です。
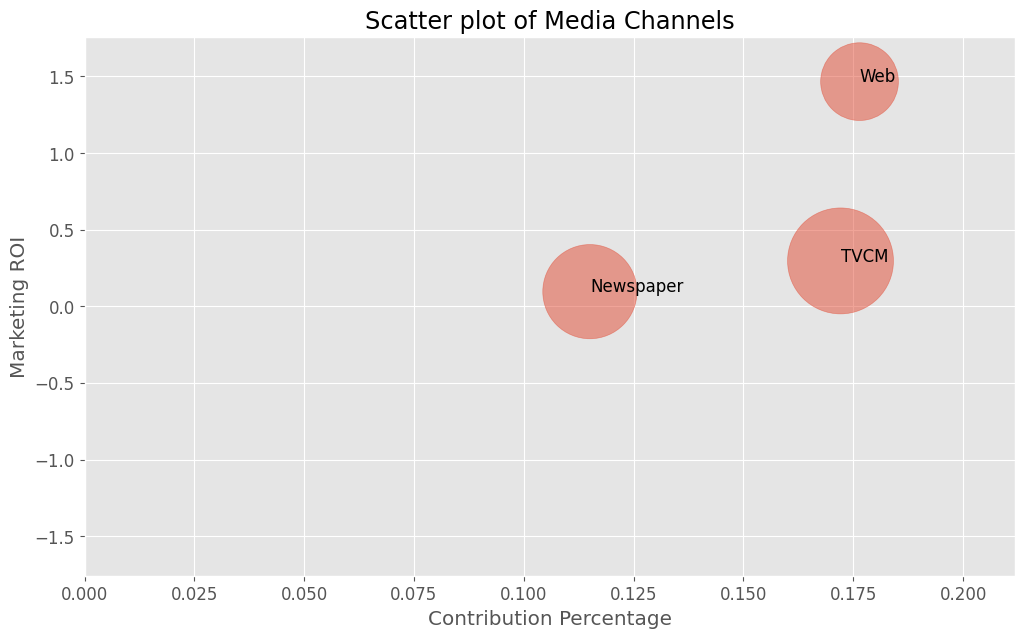
contribution_percentage ROI cost Newspaper 0.115044 0.095115 45986200.0 TVCM 0.172101 0.295622 58147500.0 Web 0.176430 1.465170 31329300.0
最適投資配分
構築したRidge MMMMパイプラインを最大化する最適投資配分問題を解き、広告・販促のコストの最適投資配分を求めます。
最後に、現状と最適化後の結果を比較し、どのような変化が起こるかを出力します。
最適化する期間は、直近1年間(52週間)です。
最適投資配分問題の設定と最適化
最適化する直近1年間(52週間)のデータを抽出します。
以下、コードです。
# 最適化期間を表す変数、ここでは直近1年間(52週間)を指定 term = 52 # 最適化期間における対象特徴量Xのデータを抽出 X_before = X[-term:] # 最適化期間における目的変数yのデータを抽出 y_before = y[-term:] # 総投資額(直近1年) cost_budget = X_before.values.ravel().sum()
- 最適化期間を表す変数の定義:
term = 52は最適化を行う期間を週単位で指定しています。- ここでは52週、つまり1年間を意味します。
- 対象特徴量Xのデータ抽出:
X_before = X[-term:]は、配列やリスト(またはPandasのDataFrameやSeriesのようなデータ構造)に含まれる対象特徴量Xから、最後のterm個の要素を抽出します。- この場合、直近52週間のデータを取り出します。
- 目的変数yのデータ抽出:
y_before = y[-term:]は、目的変数yからも同様に最後のterm個のデータを抽出します。- これにより、特徴量Xのデータと同じ期間の目的変数yのデータが得られます。
- 総投資額の計算:
cost_budget = X_before.values.ravel().sum()は、抽出した特徴量Xのデータ(X_before)から値を平坦化(ravel()を使用して1次元配列に変換)し、その合計を計算します。- この合計は
cost_budgetとして保存され、直近1年間の総投資額を表します。
ScyPyで、MMMパイプラインの出力である売上を全体コスト一定(現在のコストを合計した値)のもとで最大化する、非線形最適問題を定義し、最適解を求めます。
以下、コードです。
#
# 最適投資配分
#
niter=100
# プログレスバーを表示するための関数
def callback(xk, f, accept):
progression.update(1)
# プログレスバーを表示するためのインスタンス
progression = tqdm.tqdm(
total=niter, position=0, leave=True)
# 目的関数の定義
def objective_function(x):
# xをデータフレームに変換
x_pd = pd.DataFrame(
x.reshape(term, len(X_before.columns)),
index=X_before.index,
columns=X_before.columns)
# 予測値の計算
pred_value = trained_model.predict(x_pd)
# 目的関数の値(予測値の和の負値)を返す
return -1*pred_value.sum()
# 元の総投資額の計算
cost_all = cost_budget
# 制約条件の定義:総投資額が同じになるように
constraint = {"type":"eq","fun": lambda x: cost_all-x.sum()}
# 投資額の上限と下限の定義
lower = [0] * X_before.size
upper = [np.inf] * X_before.size
# minimizer_kwargsの設定
minimizer_kwargs = dict(
method="SLSQP",
bounds=Bounds(lower, upper),
constraints=(constraint))
# 初期解の設定
x_0 = X_before.values.ravel()
# 初期解の目的関数値の合計の負値
init_obj_value = -1 * objective_function(x_0)
# 目的関数の再定義(初期解より改善)
def revised_objective_function(x):
obj_value = objective_function(x)
return obj_value if obj_value <= init_obj_value else np.inf
# 最適化の実行
optimizeResult = basinhopping(
revised_objective_function,
x_0,
minimizer_kwargs=minimizer_kwargs,
niter=niter,
T=10,
stepsize=100000,
seed=0,
callback=callback)
# プログレスバーを閉じる
progression.close()
このコードは、特定の制約条件の下で目的関数を最適化するためのプロセスを示しています。
この場合、目的は最適な投資配分を見つけることであり、その過程で進捗状況を示すプログレスバーを使用しています。
初期設定
niter=100: 最適化処理を行う際の繰り返し回数を指定しています。progressionオブジェクト: 処理の進行状況を表示するためのプログレスバーを設定しています。
目的関数の定義
objective_function: この関数は、投資配分(x)を受け取り、その配分に基づいて予測される値(pred_value)の合計の負値を目的関数の値として返します。- 目的関数を最小化することで、予済みの値の合計を最大化します。
制約条件
- 総投資額が元の予算(
cost_budget)と同じになるように制約を設定しています。 - これは、投資額の合計が特定の予算内に収まるようにするためです。
最適化の設定
- 投資額の上限と下限: 投資額には下限(0)と上限(無限大)が設定されています。
minimizer_kwargs: 最適化手法(SLSQP)、境界条件、および制約条件を含む辞書型で、最適化関数に渡されます。basinhoppingアルゴリズムを使用して、与えられた目的関数を全局的に最適化します。このアルゴリズムは、局所最適解に陥ることなく、より良い解を探索するためにランダムなステップを使用します。
最適化の実行
basinhopping関数を使用して、目的関数の最適化を行います。ここでは、初期解からスタートして、設定された繰り返し回数(niter)、温度(T)、ステップサイズ(stepsize)、および乱数の種(seed)を基に最適化を実行します。- 最適化の進行状況は
callback関数によってプログレスバーに表示されます。 - 最適化が終了すると、プログレスバーは閉じられます。
このコードは、最適化プロセスの進行状況をユーザーに視覚的に示しながら、特定の制約条件の下で予測値の合計を最大化するような投資配分を見つけることを目的としています。最適化アルゴリズム、目的関数、制約条件の設定は、問題の性質や求める解に応じて調整することができます。
最適化の計算が終了したら、その最適解を取得します。
以下、コードです。
#
# 最適解の取得
#
# 予測結果から最適化後の値をDataFrameに変換
X_optimized = pd.DataFrame(
optimizeResult.x.reshape(len(X_before), len(X_before.columns)),
index=X_before.index,
columns=X_before.columns)
print(X_optimized)
このコードは、最適化プロセスを通じて得られた最適解(optimizeResult.x)を、元のデータと同じ形式のPandas DataFrameに変換し、表示するための処理です。
- 最適解の変換:
optimizeResult.x.reshape(len(X_before), len(X_before.columns)):optimizeResult.xには最適化アルゴリズムによって求められた最適解の値が格納されています。- この最適解は1次元の配列として得られますが、
reshapeメソッドを使用して元の特徴量データX_beforeと同じ形状(行数と列数)に変換します。 len(X_before)はX_beforeの行数、len(X_before.columns)は列数を示します。- これにより、最適化された投資配分を元のデータフレームの形式で再構成します。
- DataFrameへの変換:
pd.DataFrame(...): 変換した最適解の配列を、新しいPandas DataFrameに変換します。- このDataFrameは
X_optimizedとして保存され、index=X_before.indexとcolumns=X_before.columnsを使用して、元のデータフレームX_beforeのインデックス(行ラベル)とカラム(列ラベル)を維持します。 - これにより、最適化後のデータがどのように変更されたかを、元のデータの文脈で直接確認することができます。
- 最適化後のデータの表示:
print(X_optimized): 最終的に変換されたDataFrameX_optimizedを出力します。- これにより、最適化プロセスの結果として得られた投資配分を確認することができます。
以下、実行結果です。
TVCM Newspaper Web Week 2018-12-30 421879.259505 248446.938152 113025.249923 2019-01-06 215133.672095 203925.548971 103116.791237 2019-01-13 386674.296084 176923.092102 99362.917383 2019-01-20 294706.213830 210981.668473 112012.395489 2019-01-27 242397.437976 297574.358682 90725.744704 2019-02-03 360847.054197 229828.224229 88262.354769 2019-02-10 179725.680245 302523.189885 121060.062891 2019-02-17 350367.417719 242408.844987 94386.873288 2019-02-24 361590.825991 440799.870288 100479.853068 2019-03-03 292263.744815 169193.675243 87440.086544 2019-03-10 487151.541831 182855.037965 113321.506157 2019-03-17 77915.390661 267126.713238 96411.550915 2019-03-24 432156.033214 164290.946683 95389.124747 2019-03-31 188296.585178 229985.065370 108659.542430 2019-04-07 202031.947037 239709.612151 100117.829484 2019-04-14 584334.674557 210096.941371 107090.581867 2019-04-21 44403.102732 226814.947713 97343.796851 2019-04-28 398346.715539 304177.847549 95357.270075 2019-05-05 267296.875719 147014.770404 99036.536740 2019-05-12 378901.042386 194516.269158 100184.604006 2019-05-19 163034.387939 264784.052300 119623.420841 2019-05-26 256360.279216 281832.108960 92037.259233 2019-06-02 347421.649964 224534.759376 107970.923212 2019-06-09 314107.106905 262469.796653 90697.991473 2019-06-16 199484.501704 141146.960876 102436.110780 2019-06-23 324689.264091 236896.991331 113136.647032 2019-06-30 419942.071682 208591.912064 111021.623405 2019-07-07 373364.126358 257362.276486 100716.052098 2019-07-14 217294.635661 171205.722487 92799.760730 2019-07-21 452364.715788 246000.342588 94949.124080 2019-07-28 127883.458055 188893.668970 83237.511052 2019-08-04 410241.794253 222613.618865 100196.290270 2019-08-11 233266.936449 183411.699005 111961.592470 2019-08-18 338962.507001 271794.474876 114124.873658 2019-08-25 297369.016920 242560.252248 111233.777730 2019-09-01 293814.930024 269053.490689 112936.055803 2019-09-08 239572.022331 215001.902926 96148.391350 2019-09-15 449242.175368 222913.402263 85118.486961 2019-09-22 125534.758858 265040.967122 112740.504848 2019-09-29 419728.670677 250728.448144 114327.988367 2019-10-06 256400.475554 301157.519100 95056.739518 2019-10-13 209319.646246 213330.036451 98573.587268 2019-10-20 380423.426870 238469.837541 106287.654049 2019-10-27 186761.486108 210387.999438 91695.808198 2019-11-03 288181.616159 371865.973165 97705.877201 2019-11-10 374438.731433 209764.306806 93901.212565 2019-11-17 186034.713380 228694.065487 126304.075669 2019-11-24 537282.882838 295941.030788 87478.688795 2019-12-01 305122.039016 226632.479373 113007.085129 2019-12-08 260126.541572 231531.915762 99488.453464 2019-12-15 388427.195020 220199.420746 79055.884649 2019-12-22 52070.137148 254294.654650 100658.813489
最適投資配分の最適化結果の出力
現状と最適化の結果を比較していきます。
先ずは、売上金額です。
以下、コードです。
#
# 現状と最適配分時のyの比較
#
# 総投資額
cost_all = cost_budget
# yの実測値の合計
y_before_sum = round(y_before.sum())
# 修正比率の計算(実測のyと予測の比)
correction_ratio = y_before.sum()/trained_model.predict(X_before).sum()
# 最適配分時のyの合計
pred = trained_model.predict(X_optimized)
y_optimized_sum = round(pred.sum()*correction_ratio)
# 変化率の計算
y_change_percent = ((y_optimized_sum - y_before_sum) / y_before_sum) * 100
# 数字を表示(yの実測値と最適配分時のyの比較)
print(f"Actual - Sum of y: {y_before_sum}")
print(f"Optimized - Sum of y: {y_optimized_sum}")
sign = '+' if y_change_percent >= 0 else '-'
print(f"Percentage increase/decrease: {sign}{abs(y_change_percent):.2f}%")
# グラフ化(yの実測値と最適配分時のyの比較)
labels = ['Actual', 'Optimized']
values = [y_before_sum, y_optimized_sum]
plt.figure()
bars = plt.bar(labels, values, color=['blue', 'orange'])
plt.title('Comparison of y: Actual vs. Optimized')
plt.ylabel('y')
for bar in bars:
height = bar.get_height()
plt.text(bar.get_x() + bar.get_width() / 2.0, height, f'{int(height)}', ha='center', va='bottom')
plt.show()
このコードで、最適化前後の目的変数yの合計値を比較し、その変化率を計算して表示することで、最適化がyに与えた影響を評価するための処理します。
前提条件
cost_all = cost_budget: 総投資額が設定されています。これは、投資の制約として用いられる総予算です。y_before_sum: 現状の投資戦略におけるyの実測値の合計を計算しています。
修正比率の計算
- 修正比率を計算することで、予測モデルが出力する値と実際の値との間のスケールの違いを調整します。
- これは、モデルの予測値が実測値と完全に一致しない可能性があるため、予測値を修正するために使用されます。
最適配分時のyの合計
X_optimizedに基づいて予測されるyの合計を計算し、修正比率を適用して、最適配分時のyの合計値を修正します。
変化率の計算
- 現状の
yの合計値と最適化後のyの合計値の間の変化率を計算します。 - この変化率はパーセンテージで表され、最適化によって
yがどれだけ改善されるかを示します。
結果の表示
- 現状と最適化後の
yの合計値、およびその変化率を表示します。 - 変化率が正の場合は増加、負の場合は減少を示します。
グラフ化
- 最後に、
matplotlibライブラリを使用して、現状と最適化後のyの合計値を比較するバーグラフを描画します。 - このグラフは、数値的な比較に加えて視覚的な比較も提供し、最適化の影響を直感的に理解するのに役立ちます。
以下、実行結果です。
Actual - Sum of y: 109594445 Optimized - Sum of y: 129521041 Percentage increase/decrease: +18.18%
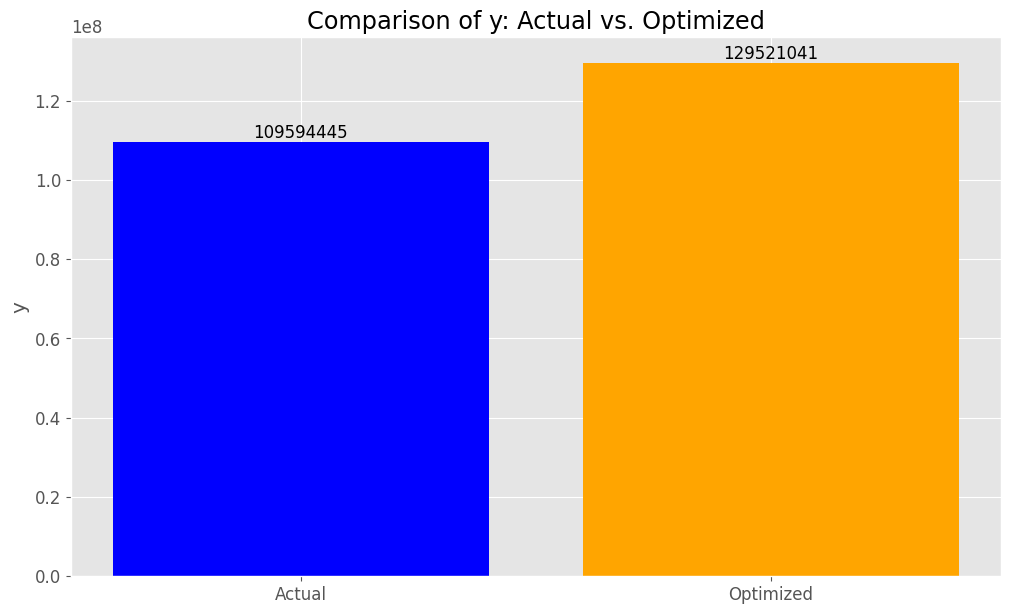
次に、マーケティングROIです。
以下、コードです。
#
# 現状と最適配分時のマーケティングROIの比較
#
# 現状のマーケティングROI
roi_actual = ((y_before_sum - cost_all) / cost_all)
# 最適配分時のマーケティングROI
roi_optimized = ((y_optimized_sum - cost_all) / cost_all)
# 変化ポイントの計算
roi_change_point = roi_optimized - roi_actual
# 数字を表示(現状と最適配分時のマーケティングROIの比較)
print(f"Actual - Marketing ROI: {roi_actual:.2f}")
print(f"Optimized - Marketing ROI: {roi_optimized:.2f}")
sign = '+' if roi_change_point >= 0 else '-'
print(f"Point increase/decrease: {sign}{abs(roi_change_point):.2f}point")
# グラフ化(現状と最適配分時のマーケティングROIの比較)
labels = ['Actual', 'Optimized']
values = [roi_actual, roi_optimized]
plt.figure(figsize=(10, 6))
bars = plt.bar(labels, values, color=['blue', 'orange'])
plt.title('Comparison of Marketing ROI: Actual vs. Optimized')
plt.ylabel('ROI')
for bar in bars:
height = bar.get_height()
plt.text(bar.get_x() + bar.get_width() / 2.0, height, f'{height:.2f}', ha='center', va='bottom')
plt.show()
このコードで、マーケティングの投資収益率(ROI)を最適化前(現状)と最適化後(最適配分時)で比較し、その変化を計算して表示します。
ここでのROIは、得られた利益(yの合計から総投資額を引いた値)を投資額で割ったものです。
現状のマーケティングROIの計算
roi_actual = ((y_before_sum - cost_all) / cost_all): 最適化前のyの合計値から総投資額を引き、その結果を再度総投資額で割ることで、現状のマーケティングROIを計算します。
最適配分時のマーケティングROIの計算
roi_optimized = ((y_optimized_sum - cost_all) / cost_all): 最適化後のyの合計値から総投資額を引き、その結果を再度総投資額で割ることで、最適配分時のマーケティングROIを計算します。
ROIの変化の計算
roi_change_point = roi_optimized - roi_actual: 最適化後のROIから最適化前のROIを引くことで、ROIの変化量を計算します。
結果の表示
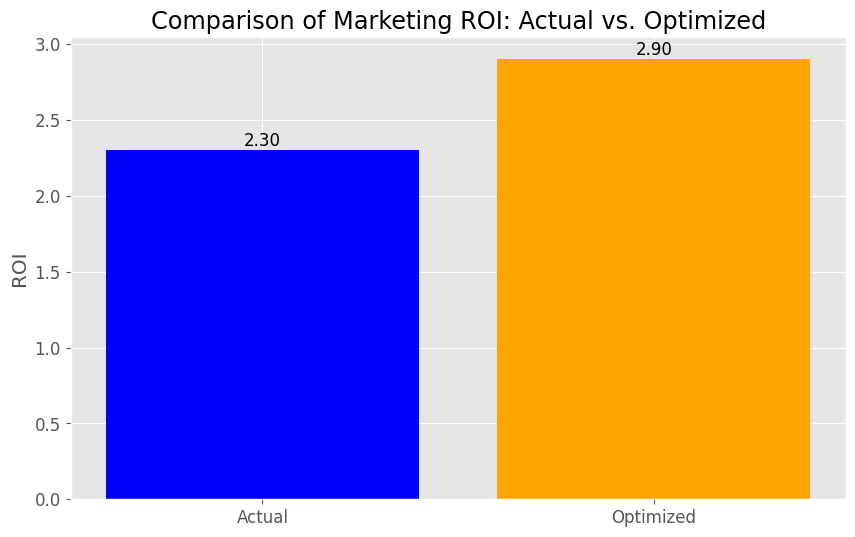
数値による比較: 現状のROI、最適化後のROI、およびROIの変化量(ポイントでの増減)を表示します。変化量が正の場合は+記号を、負の場合は-記号を付けて表示します。グラフによる比較: plt.barを使用して、最適化前後のマーケティングROIを棒グラフで比較します。各棒の上にはその高さ(ROI)を小数点以下2桁まで表示しています。
以下、実行結果です。
Actual - Marketing ROI: 2.30 Optimized - Marketing ROI: 2.90 Point increase/decrease: +0.60point
最後に、投資配分です。
以下、コードです。
#
# 投資配分構成比の比較
#
# 最適化前(実投資)の構成比
X_before_ratio = X_before.sum()/X_before.sum().sum()
# 最適投資の構成比
X_optimized_ratio = X_optimized.sum()/X_optimized.sum().sum()
# 構成比の表示
comparison_df = pd.DataFrame({
'Actual Allocation': X_before_ratio,
'Optimized Allocation': X_optimized_ratio})
print((comparison_df * 100).round(1).astype(str) + '%')
# グラフ化
fig, ax = plt.subplots()
bottom = np.zeros(2)
for value, feature in zip(comparison_df.values, X.columns):
ax.bar(['Actual', 'Optimized'], value, bottom=bottom, label=feature)
bottom += value
ax.set_title('Media Cost Allocation')
ax.set_ylabel('% of Total Investment')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles[::-1], labels[::-1])
ax.set_ylim([0, 1])
plt.show()
このコードで、最適化前と最適化後の投資配分の構成比を比較し、その差異を数値的および視覚的にアウトプットします。
具体的には、各特徴量(例えば、マーケティングメディアの種類など)に対する投資額の全投資額に占める割合(構成比)を計算し、これらの構成比を現状(実投資)と最適化後(最適投資)で比較します。
投資配分の構成比の計算
X_before_ratio = X_before.sum()/X_before.sum().sum(): 最適化前のデータフレームX_beforeにおける各列(特徴量)の合計を計算し、これらの合計値の総合計で割ることで、各特徴量の全投資額に占める割合を求めます。X_optimized_ratio = X_optimized.sum()/X_optimized.sum().sum(): 同様に、最適化後のデータフレームX_optimizedで各特徴量の構成比を計算します。
構成比の表示
次に、計算した構成比をpd.DataFrameを用いて1つのデータフレームにまとめ、'Actual Allocation'と'Optimized Allocation'の2列として整理します。(comparison_df * 100).round(1).astype(str) + '%': 構成比をパーセンテージ形式で表示しやすくするために、100を乗じてパーセント表示に変換し、小数点以下1位で四捨五入し、最後に%記号を追加して文字列としてフォーマットします。
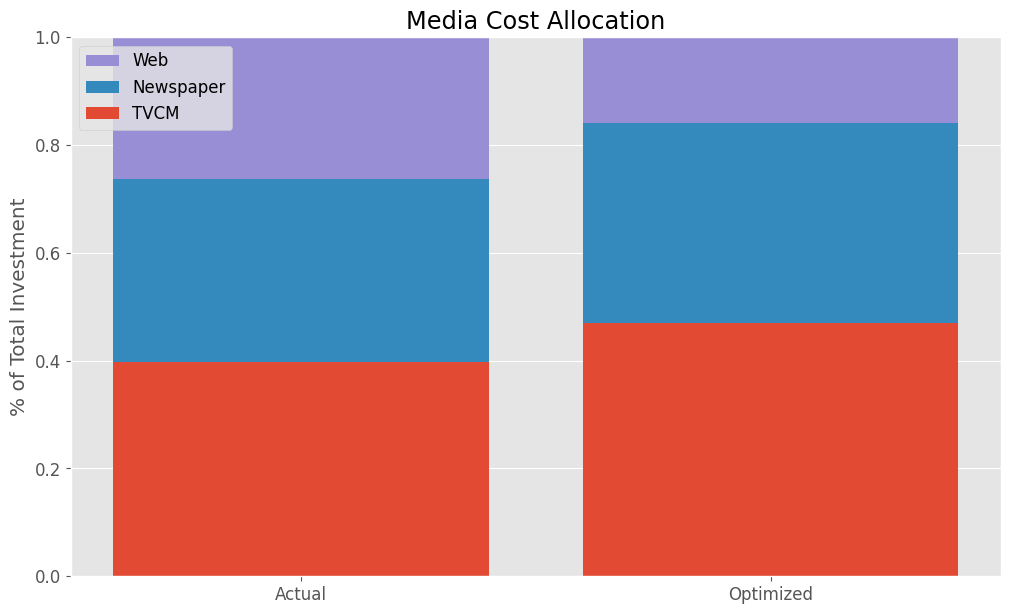
グラフ化
棒グラフを用いて、最適化前後の各特徴量の構成比を視覚的に比較します。ax.bar関数を使用して、'Actual'と'Optimized'の2つのカテゴリについて、各特徴量の構成比を積み上げ棒グラフとして描画します。bottomパラメータを使って各特徴量のバーを前のバーの上に積み上げていきます。凡例、タイトル、y軸ラベルを設定し、y軸の範囲を0から1(0%から100%)に設定しています。
以下、実行結果です。
Actual Allocation Optimized Allocation TVCM 39.7% 47.0% Newspaper 33.9% 37.1% Web 26.4% 15.9%
まとめ
今回は、線形回帰系MMM(Ridge MMMパイプライン)を構築した後に、特徴量(説明変数)Xである広告・販促コストの最適投資配分の求め方を説明しました。
具体的には、全体コスト一定のもとで売上を最大化する非線形計画問題を解きました。
ただ、特徴量(説明変数)Xのすべてが、アドストックを考慮し最適化すべき広告・販促コストのデータでないかもしれません。
例えば、カレンダー情報を元にした特徴量(例:クリスマス変数、初売り初日変数などの○○の日)や、季節性を表現する三角関数特徴量(SinとCosで表現)などは、アドストックを考慮すべきでないかもしれませんし、最適化対象となるコストデータでもありません。
要するに、各特徴量(説明変数)の特性に応じて、MMMを構築するときに「アドストックを考慮すべき or アドストックを考慮すべきでない」、「最適化対象となるコストデータ or そうではない」を選べるといいでしょう。
ということで、次回は「アドストックを考慮すべきどうか、コスト最適化の対象かどうか、特徴量を指定し構築する線形回帰系MMM」というお話しをします。
PythonによるMMM(マーケティングミックスモデリング)とビジネス活用- 振返り分析・最適投資配分編(その2)-線形回帰系MMMの最適投資配分(特徴量指定・ハイパラ付与)

