- 問題
- 答え
- 解説
Python コード:
from statsmodels.tsa.stattools import coint
import numpy as np
np.random.seed(42)
x = np.random.randn(100).cumsum()
y = x + np.random.randn(100)
coint_t, p_value, crit_value = coint(x, y)
print(f'Cointegration test statistic: {coint_t}')
print(f'p-value: {p_value}')
回答の選択肢:
(A) p値が0.01未満
(B) p値が0.01以上0.05未満
(C) p値が0.05以上0.10未満
(D) p値が0.10以上
Cointegration test statistic: -10.546923889518611 p-value: 1.0672395686753766e-17
正解: (A)
回答の選択肢:
(A) p値が0.01未満
(B) p値が0.01以上0.05未満
(C) p値が0.05以上0.10未満
(D) p値が0.10以上
- コードの解説
-
このコードは、Engle-Grangerの二変量共和分検定を実行しています。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterfrom statsmodels.tsa.stattools import cointimport numpy as npnp.random.seed(42)x = np.random.randn(100).cumsum()y = x + np.random.randn(100)coint_t, p_value, crit_value = coint(x, y)print(f'Cointegration test statistic: {coint_t}')print(f'p-value: {p_value}')from statsmodels.tsa.stattools import coint import numpy as np np.random.seed(42) x = np.random.randn(100).cumsum() y = x + np.random.randn(100) coint_t, p_value, crit_value = coint(x, y) print(f'Cointegration test statistic: {coint_t}') print(f'p-value: {p_value}')
from statsmodels.tsa.stattools import coint import numpy as np np.random.seed(42) x = np.random.randn(100).cumsum() y = x + np.random.randn(100) coint_t, p_value, crit_value = coint(x, y) print(f'Cointegration test statistic: {coint_t}') print(f'p-value: {p_value}')Engle-Grangerの共和分検定では、2つの時系列が共に1次の非定常過程である一方で、その間の線形組み合わせが定常過程であるかどうかを検定します。
これは、「一緒に動く」ことを示すことができるため、共和分は関連する時系列間の長期的な均衡関係を捉えるのに有用です。
詳しく説明します。
まず、
randomでランダムに生成された100要素の配列を生成します。cumsum()関数を使って累積和を取り、1次の非定常過程のデータ(ランダムウォーク)を生成します。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighternp.random.seed(42)x = np.random.randn(100).cumsum()np.random.seed(42) x = np.random.randn(100).cumsum()np.random.seed(42) x = np.random.randn(100).cumsum()
xに格納されているデータは次のようになっています。[ 0.49671415 0.35844985 1.00613839 2.52916825 2.29501487 2.06087791 3.64009073 4.40752546 3.93805107 4.48061112 4.01719342 3.55146367 3.79342594 1.8801457 0.15522787 -0.40705966 -1.41989078 -1.10564345 -2.01366753 -3.42597123 -1.96032246 -2.18609876 -2.11857056 -3.54331874 -4.08770147 -3.97677888 -5.12777245 -4.75207444 -5.35271313 -5.64440688 -6.24611349 -4.3938353 -4.40733253 -5.46504346 -4.64249854 -5.86334219 -5.6544786 -7.61414872 -8.94233477 -8.74547354 -8.00700696 -7.83563868 -7.95128696 -8.25239065 -9.73091264 -10.45075685 -10.91139562 -9.8542734 -9.51065511 -11.27369526 -10.94961129 -11.33469357 -12.01161557 -11.39993929 -10.36893976 -9.43765964 -10.27687717 -10.58608954 -10.25482611 -9.27928098 -9.75845522 -9.9441142 -11.05044917 -12.2466558 -11.43412997 -10.07788995 -10.14990007 -9.14636717 -8.78473114 -9.4298509 -9.06845529 -7.53041873 -7.56624477 -6.00160111 -8.62134621 -7.79944371 -7.71239664 -8.01140399 -7.91964322 -9.90721213 -10.12688402 -9.76977145 -8.2918774 -8.81014762 -9.61864122 -10.12039827 -9.20499615 -8.87624504 -9.40600524 -8.89273781 -8.79566026 -7.82701527 -8.52906836 -8.85673051 -9.24883866 -10.71235361 -10.41623333 -10.15517806 -10.15006461 -10.38465174]
2つ目の時系列
yは、最初の時系列xにランダムノイズ(ここでは0平均、標準偏差1の正規分布からのランダムな値)を追加することで生成されます。このノイズ項があることで、xとyの間にある程度のばらつきが生じます。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlightery = x + np.random.randn(100)y = x + np.random.randn(100)y = x + np.random.randn(100)
yに格納されているデータは次のようになっています。[ -0.91865659 -0.06219547 0.66342387 1.72689098 2.13372916 2.46492877 5.52627663 4.58210327 4.19560146 4.4061652 2.09842221 3.5249498 3.85365615 4.34338781 -0.0371331 -0.10551232 -1.45460255 -2.27432149 -0.87084471 -2.6740382 -1.16929051 -3.09548622 -0.71577624 -4.9451698 -3.50084437 -1.78632325 -6.11830878 -5.31837217 -5.25306176 -6.14788253 -7.79677692 -4.32527233 -5.46963624 -4.99145103 -5.56192278 -4.31340779 -6.43773189 -7.93621024 -8.12881756 -9.97633785 -7.77954702 -6.52849592 -9.55877019 -8.06775679 -9.47102985 -9.66893398 -12.14834633 -11.17473001 -8.98871354 -10.97671059 -10.69911844 -10.98824536 -12.6916403 -11.16768559 -10.07586729 -10.15201106 -8.41110266 -10.11225662 -11.44612961 -8.62272738 -10.73313689 -9.15702959 -9.89185359 -13.06733812 -10.47075385 -9.66510902 -9.32783991 -7.24957419 -9.03011926 -10.18358706 -9.95796972 -8.34622901 -7.64334648 -5.66044914 -8.34465542 -6.97226046 -7.69939475 -6.55786992 -8.18430005 -7.18704296 -9.50121667 -10.626929 -9.3627699 -8.32767521 -9.84210401 -9.40639777 -8.73175852 -8.94907395 -10.25279896 -10.40758503 -9.24217521 -6.97061648 -8.31497462 -10.10246929 -9.07565774 -10.32703623 -11.30009077 -10.00145296 -10.09185589 -11.52762204]
参考までに、
xとyの折れ線グラフです。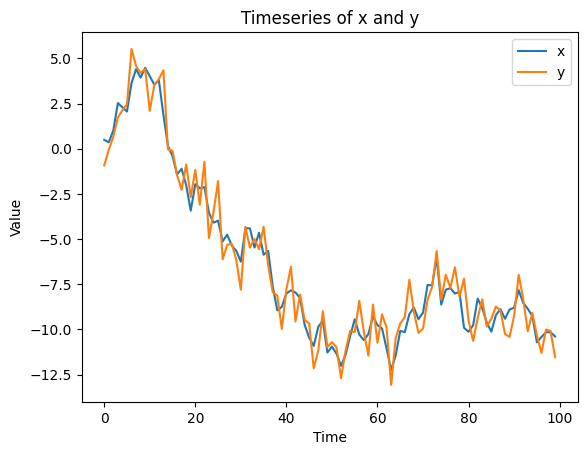
そのように作ったのですから当然ですが、明らかに
xとyは共和分の関係にあります。
statsmodelsのcoint関数を使って2つの時系列xとyの間のEngle-Grangerの二変量共和分検定を実行します。この関数は共和分統計量(そしてそれに対応するp値)と、様々な信頼度での臨界値を返します。Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlightercoint_t, p_value, crit_value = coint(x, y)coint_t, p_value, crit_value = coint(x, y)coint_t, p_value, crit_value = coint(x, y)
ちなみに、
coint関数の戻り値は次の3つです。coint_t:共和分検定統計量です。この値が小さいほど(負の大きいほど)、2つの時系列が共和分している可能性が高いです。p_value:p値です。この値が小さいほど(例えば0.05より小さい)、2つの時系列が共和分していると判断できます。crit_value:有意水準に対応する臨界値です。共和分検定統計量がこれらの値よりも小さい場合(絶対値が大きい場合)、対応する信頼水準で帰無仮説(つまり、データが共和分せず、個別に非定常である)を棄却することができます。
共和分検定の統計量とp値を出力します。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterprint(f'Cointegration test statistic: {coint_t}')print(f'p-value: {p_value}')print(f'Cointegration test statistic: {coint_t}') print(f'p-value: {p_value}')print(f'Cointegration test statistic: {coint_t}') print(f'p-value: {p_value}')Cointegration test statistic: -10.546923889518611 p-value: 1.0672395686753766e-17
出力結果から、共和分検定の統計量は約-10.55で、p値は約0.00となっています。p値が低い(例えば0.05以下)場合には帰無仮説(ここでは「2つの時系列は共和分していない」)を棄却します。
今回の結果はp値が約0.00となっているため、帰無仮説を棄却し「この2つの時系列が共和分する」と結論付けらます。
- 見せかけの回帰
-
Contents [hide]
見せかけの回帰とは?
見せかけの回帰(spurious regression)は、2つ以上の非定常な時系列データ間に偽の統計的関連性が存在するように見える現象です。
これは通常、データがランダムウォークプロセスや他の一般的な非定常なプロセスに従っている場合に発生します。
非定常な時系列データを回帰分析に使用すると、統計的推測が無効になる可能性があります。
具体的にはt統計量が正常に機能せず、β係数が有意であると誤って判断してしまう可能性があります。これが見せかけの回帰です。
簡単なPythonデモ
乱数で2つのランダムウォークの時系列データを作り、一方を目的変数、他方を説明変数とする回帰分析を実施します。
この2つのランダムウォークデータは本来は無関係ですので、回帰係数は有意でない(係数が0とみなせる)はずです。
先ず、乱数で2つのランダムウォークの時系列データを生成します。
以下、コードです。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterimport numpy as npimport matplotlib.pyplot as pltfrom statsmodels.api import OLSimport statsmodels.api as sm# 乱数で2つのランダムウォークの時系列データを生成np.random.seed(42)x = np.random.normal(0, 1, 100).cumsum()y = np.random.normal(0, 1, 100).cumsum()import numpy as np import matplotlib.pyplot as plt from statsmodels.api import OLS import statsmodels.api as sm # 乱数で2つのランダムウォークの時系列データを生成 np.random.seed(42) x = np.random.normal(0, 1, 100).cumsum() y = np.random.normal(0, 1, 100).cumsum()import numpy as np import matplotlib.pyplot as plt from statsmodels.api import OLS import statsmodels.api as sm # 乱数で2つのランダムウォークの時系列データを生成 np.random.seed(42) x = np.random.normal(0, 1, 100).cumsum() y = np.random.normal(0, 1, 100).cumsum()
プロットしてみます。
以下、コードです。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighterplt.figure(figsize=(12, 6))plt.plot(x, label='x')plt.plot(y, label='y')plt.title('Random walks x and y')plt.xlabel('Time')plt.ylabel('Value')plt.legend()plt.show()plt.figure(figsize=(12, 6)) plt.plot(x, label='x') plt.plot(y, label='y') plt.title('Random walks x and y') plt.xlabel('Time') plt.ylabel('Value') plt.legend() plt.show()plt.figure(figsize=(12, 6)) plt.plot(x, label='x') plt.plot(y, label='y') plt.title('Random walks x and y') plt.xlabel('Time') plt.ylabel('Value') plt.legend() plt.show()以下、実行結果です。
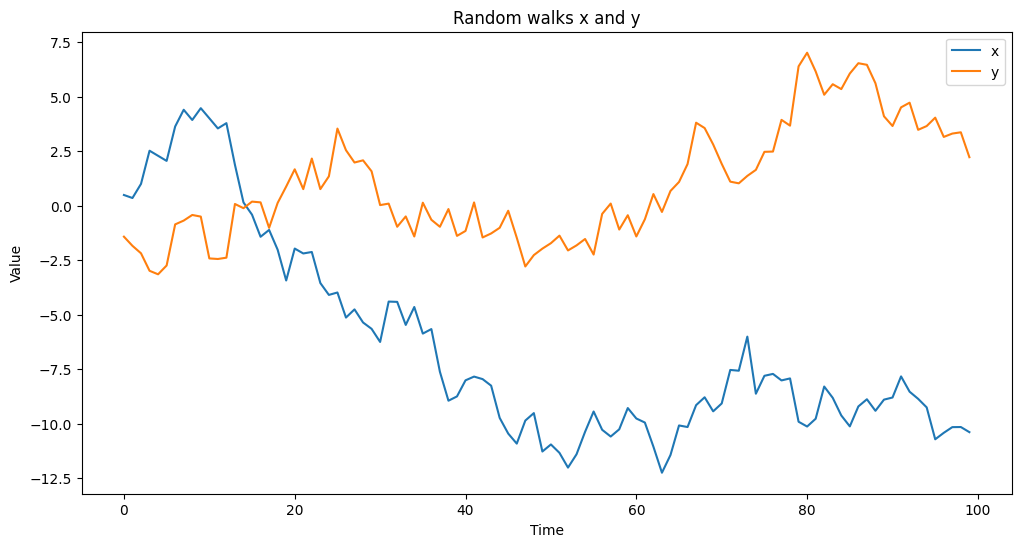
単回帰分析を実施します。
以下、コードです。
Plain textCopy to clipboardOpen code in new windowEnlighterJS 3 Syntax Highlighter# 単回帰分析X = sm.add_constant(x) # 切片追加model = OLS(y, X)results = model.fit()# 結果出力print(results.summary())# 単回帰分析 X = sm.add_constant(x) # 切片追加 model = OLS(y, X) results = model.fit() # 結果出力 print(results.summary())# 単回帰分析 X = sm.add_constant(x) # 切片追加 model = OLS(y, X) results = model.fit() # 結果出力 print(results.summary())
以下、実行結果です。
OLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.135 Model: OLS Adj. R-squared: 0.126 Method: Least Squares F-statistic: 15.32 Date: Mon, 04 Mar 2024 Prob (F-statistic): 0.000168 Time: 11:57:18 Log-Likelihood: -230.02 No. Observations: 100 AIC: 464.0 Df Residuals: 98 BIC: 469.2 Df Model: 1 Covariance Type: nonrobust ============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ const -0.3661 0.417 -0.879 0.382 -1.193 0.461 x1 -0.2065 0.053 -3.913 0.000 -0.311 -0.102 ============================================================================== Omnibus: 5.281 Durbin-Watson: 0.149 Prob(Omnibus): 0.071 Jarque-Bera (JB): 3.226 Skew: 0.248 Prob(JB): 0.199 Kurtosis: 2.273 Cond. No. 13.6 ==============================================================================x1行のcoef(単回帰係数)とP>|t|(p値)を見てみます。p値が0.00であることより、単回帰係数が有意であることが分かります。要するに、無関係な2つの時系列データの間に、関係性があるかのような結果になっています。
これが、見せかけの回帰です。
解決方法
これを解決する方法の一つが共和分の概念です。
共和分時間系列は、非定常な時系列ですが、一定の線形結合を通して定常な系列を生成します。言い換えれば、それらは長期的な均衡関係を共有します。
これが確認されれば、これらの変数間の回帰分析は有効となり、信頼できる結果を与えます(つまり、見せかけの回帰が避けられます)。
したがって、多変量の時系列分析を行う場合、定常性の確認と共和分の検定は重要です。これにより見せかけの回帰を避け、有効かつ信頼性のある統計的推測を行うことが可能になります。
Engle-Grangerの2変量共和分検定(`coint`関数)は、これらのステップを実行するのに役立つツールの一つです。
- 共和分検定
-
共和分とは?
平均や分散が時間とともに一定でない、つまり時間の経過とともにその統計的性質が変化する時系列のことを、非定常時系列と言います。例えば、株価や経済指標などの金融データは、トレンドや周期性などの時間依存性を持つことから、非定常な性質を持つといえます。
共和分とは、2つ以上の非定常な時系列からなるシステムがあるとき、それらの適切な線形組み合わせによって新たな時系列を生成し、その新たな時系列が定常である(つまり、その平均や分散などの統計的特性が時間とともに一定になる)場合を指します。
たとえば、2つの異なる非定常な株価時系列があるとき、一つの株価が上昇すると他の株価も上昇するというように、一方の動きが他方の動きと同期している場合、それらは共和分しているといえます。

その結果として新たに作られた時系列(つまり、一方の株価から他方の株価を引いたもの)は、時間を通じて一定の平均に戻そうとする特性を持つ、すなわち定常性を持つこともありえます。これは一種の「平均回帰」の現象で、一定の均衡状態を保とうとする経済的な力によるものと解釈することができます。
具体的には、たとえば非定常な時系列
共和分の条件では、この誤差項 ε の時系列が定常過程となる場合に、
どうやって共和分かどうかを見極めるのか?
共和分検定とは?
共和分検定(例えば、ジョハンセン検定やEngle-Grangerの2変量共和分検定など)は、指定された時系列が共和分関係性を持つかどうかを判定するために使用されます。
これらの検定は基本的に、異なる非定常時系列の線形組み合わせが定常になるかどうかをチェックします。
エンゲル・グレンジャーの二変量共和分検定
エンゲル・グレンジャーの二変量共和分検定(Engle-Granger two-step cointegration test)は、2つの時系列が共和分関係にあるかどうかを検定する方法です。
共和分関係にあるとは、2つ以上の非定常な時系列が一定の均衡関係にあるということを意味します。この関係がある場合、一つの時系列がランダムに動いても、他の時系列はそれに合わせて動き、全体としては一定の均衡状態が維持されます。
エンゲル・グレンジャーの二変量共和分検定は、以下の2つのステップからなります。
- ステップ1:まず、2つの時系列がそれぞれ単位根を持つ、つまり非定常であることを確認します。これは、通常、Dickey-FullerテストやAugmented Dickey-Fullerテストなどの単位根検定を使用して行います。
- ステップ2:ステップ1で非定常であることが確認された2つの時系列について、一方の時系列を他方の回帰変数とする線形回帰モデルを推定します。そして、その回帰残差が定常であるかどうかを再度単位根検定で確認します。もし回帰残差が定常であれば、元の2つの時系列は共和分関係にあると判断されます。
帰無仮説(H0)と対立仮説(H1)は以下のように定義されます。
- 帰無仮説(H0):2つの時系列が共和分していない。つまり、2つの時系列間に長期的な均衡関係が存在しない。
- 対立仮説(H1):2つの時系列が共和分している。つまり、2つの時系列間に長期的な均衡関係が存在する。
つまり、この検定は、帰無仮説が真である(つまり、2つの時系列が共和分していない)と仮定した場合に、観測されたデータがどれだけありえないものであるか(p値)を評価します。
もしp値が所定の有意水準(通常は5%または1%)を下回れば、帰無仮説を棄却し(つまり、2つの時系列が共和分していないという仮説を否定し)、対立仮説を採択します。
対で確認する
共和分検定を行う場合は、検定を行いたい各変数の対、つまり各組み合わせに対して独立に行います。
具体的には、一つの目的変数と一つの説明変数に対して共和分検定を行い、それを全ての説明変数に対して行います。
例えば、目的変数が一つで説明変数が3つある場合(Yに対してX1, X2, X3が存在する場合)、YとX1、YとX2、YとX3のそれぞれのペアに対して共和分検定を実行します。
ただし、これには注意が必要で、共和分検定が確認できたからといって、単純に全ての説明変数をモデルに含めるべきというわけではありません。それぞれの説明変数が目的変数に対して独立に影響を与えるわけではなく、他の説明変数と交互作用する場合もあるからです。
そのため、共和分関係を確認したあとでも、モデルの選択と調整は必要で、その一環として多重共線性のチェックなどを行うべきです。
共和分検定後
共和分検定結果をもとに時系列データのモデリングを行う方法は以下の通りです。
共和分関係が確認された場合(p値が有意水準以下)
元の時系列データは共和分関係にあります。つまり、これらの時系列は長期的な均衡関係を保つ傾向にあります。この共和分関係を利用することで、モデリングの正確性を向上させます。具体的には、誤差修正モデル(ECM: Error Correction Model)や時系列回帰モデルなどを構築します。共和分関係が確認されなかった場合(p値が有意水準を上回る)
元の時系列データは共和分関係にはありません。したがって、それぞれの時系列データは別々にモデリングするべきです。共和分関係を仮定するモデル(例えば、誤差修正モデルや時系列回帰モデルなど)を使用することは適切ではありません。このようなシナリオでよく使われるのは、ARIMA(自己回帰積分移動平均)モデルや状態空間モデルなどです。どのモデルを選択するかは、データの特性や分析の目的によります。必ずしも共和分が存在すればそのモデルを使用すべきというわけではありません。共和分が存在しない場合でも、他のモデリング手法を適切に使用すれば、有用な予測や分析を行うことができます。
- 時系列データのモデリング
-
モデルの構築手順
以下の3つの手順を踏むことで、非定常時間系列データに対する進んだレベルの分析と予測を行うことができます。
Step 1. 非定常であることを確認する
主に単位根検定(たとえば、ディッキー・フラー検定または拡張ディッキー・フラー検定)を使用して非定常性を確認します。
非定常時間系列は、時間に依存する統計的特性(たとえば、平均や分散)を持つため、これらの特性が一定(定常)であると仮定した通常の回帰分析では適切にモデリングできません。
Step 2. 共和分であることを確認する
2つ以上の非定常変数間の長期的な均衡関係を示すものを共和分と呼びます。
共和分検定は、これらの非定常な時系列変数が共和分関係にあるかどうかを検定します。一つの方法としてエングル・グレンジャーの方法などがあります。
Step 3. モデルを構築する
共和分関係が存在する場合、時系列回帰モデルや誤差修正モデル(Error Correction Model)などの共和分関係を考慮に入れたモデルを構築します。
誤差修正モデルは共和分関係を利用して、時系列の短期的な偏差と長期的な均衡状態の両方を捉えることができ、より洗練された予測が可能になります。
時系列回帰モデルと誤差修正モデル
時系列回帰モデルと誤差修正モデル(Error Correction Model, ECM)は両方とも時系列データのモデリングに使用されますが、その概念と用途は異なります。
簡潔に言うと、時系列回帰モデルは時系列データの一般的なモデリング手法であり、誤差修正モデルは特定の状況、具体的には共和分関係にある時系列をモデリングするための特化したモデルです。
時系列回帰モデル
一つの目的変数が一つまたは複数の説明変数によって予測または説明されるという基本的な回帰分析の概念を、時間オーダーに並んだデータ、すなわち時系列データに適用したものです。これは、目的変数と説明変数の両方が時間の経過とともに変化する可能性があり、これらの変化が目的変数にどのように影響するかを理解しようとするものです。
一番単純な形は単純な線形回帰モデルと同じ形式を取ります。ある時点
ただし、これは一番単純な形で、実際には自己相関や季節性などを考慮したARIMAモデルやARIMAXモデル等がよく用いられます。
誤差修正モデル(ECM)
時系列が共和分している場合、つまり共有の長期的な均衡関係が存在する場合に使用されるモデルです。ECMは、変数間の長期的な均衡関係と、その均衡からの短期的な逸脱(誤差)を同時にモデリングします。
このため、ECMは非定常な共和分シリーズをモデリングするために特に適しています。