データを活用したマーケティング戦略は、ビジネスの成功に不可欠です。その中心に位置するのが、マーケティングミックスモデリング(MMM)です。
マーケティングミックスモデリング(MMM)は、過去のデータを分析する「振り返り分析」と未来のトレンドを予測する「近未来分析」の両方で有効に活用される強力なツールです。
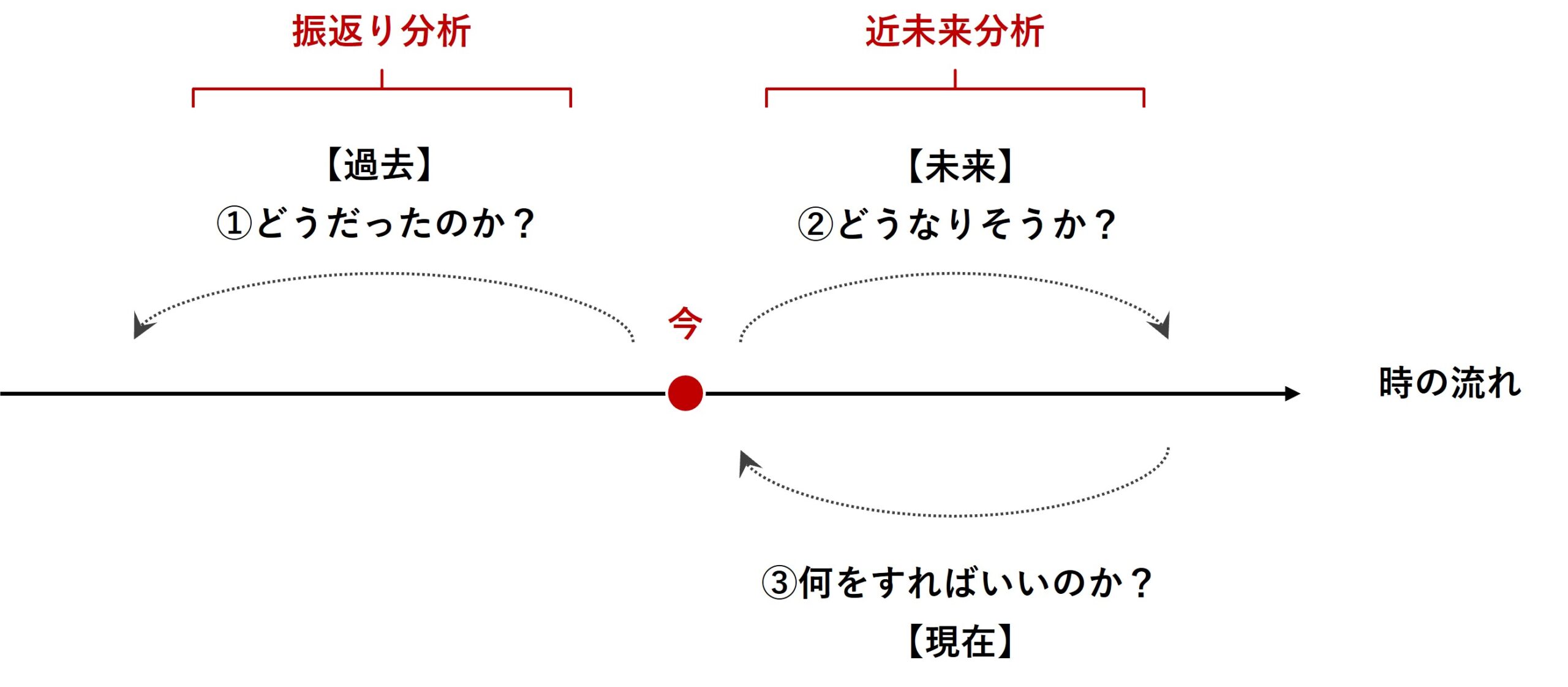
振返り分析のためのMMMは、各広告・販促の手段が、どのくらいの売上などに貢献し、それが効率的だったのかどうかを、明らかにすることでした。
さらに一歩先に話しを進め、どの広告・販促の手段に、どの程度のコストをかけて投資をするのが効率的なのか? を明らかにする振返り分析もあります。
要するに、広告・販促の手段にかけるコストの最適投資配分です。
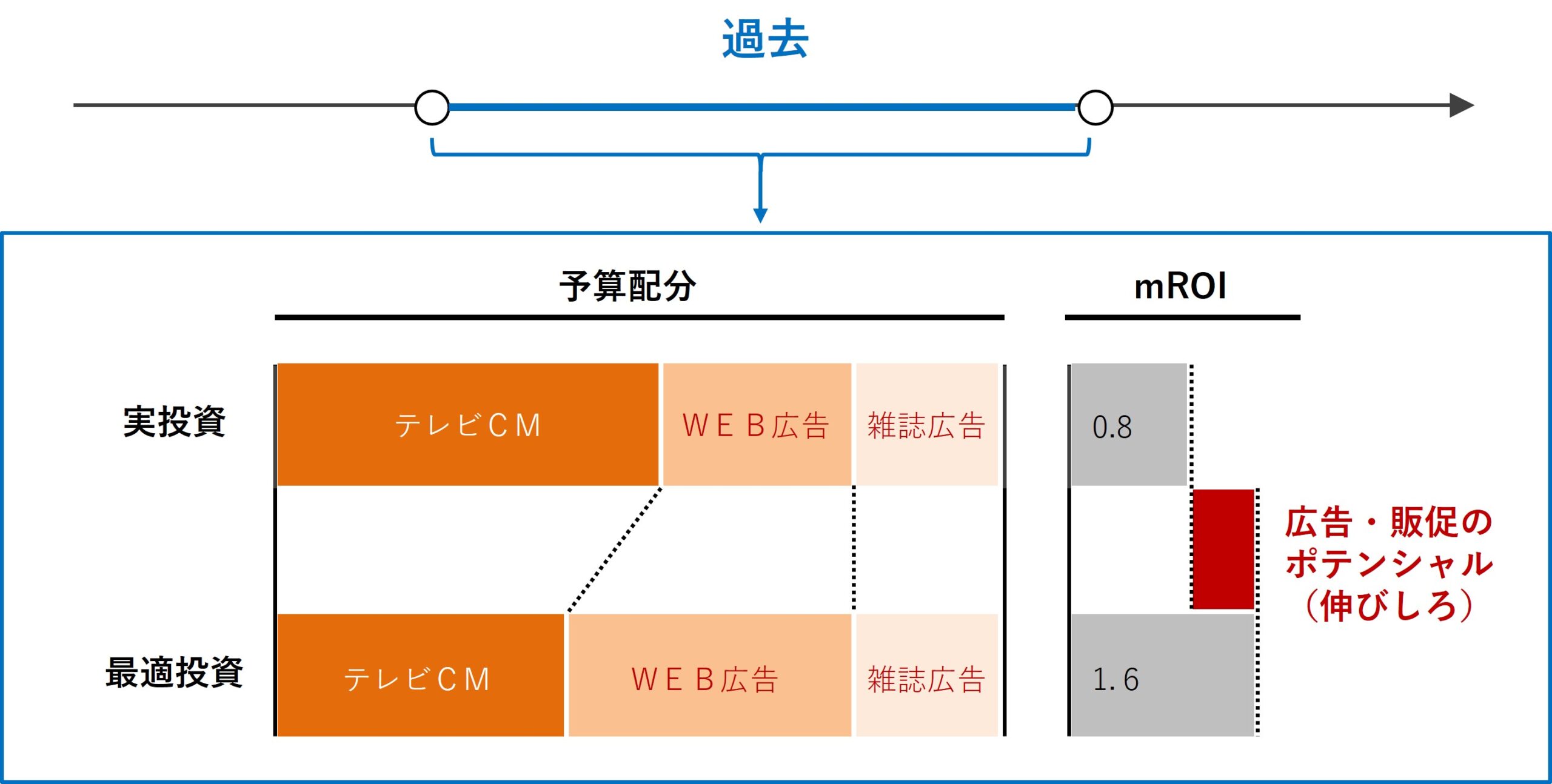
色々なアプローチがありますが、ストレートなのは非線形計画問題(非線形最適化)を定式化しソルバーで解くことです。具体的に言うと、PythonのScyPyである程度は実現することができます。
前回は「アドストックを考慮すべきどうか、コスト最適化の対象かどうか、特徴量を指定し構築する線形回帰系MMM」というお話しをします。
ただ、アドストックのハイパーパラメータを設定する方法で、Ridge MMMパイプラインを構築したため、MMMの精度がいまいちでした。
今回は、「Ridge MMMパイプラインのハイパーパラメータをOptunaで最適化し、アドストックを考慮すべきどうか、コスト最適化の対象かどうか、特徴量を指定し自動調整し構築する線形回帰系MMM」のお話しをします。
Contents [hide]
- (前回と同じ)データセットと最適投資配分
- 今回利用するデータセット
- 今回構築するMMMと最適化
- 準備
- モジュールの読み込み
- データセットの読み込み
- 目的関数作り
- アドストックを考慮する特徴量のリスト
- 最適なハイパーパラメータの探索
- (必要があれば)Optunaのstudyの保存と読み込み
- MMMパイプラインの構築
- (必要があれば)学習済みモデルの保存と読み込み
- 売上貢献度とマーケティングROI
- 最適投資配分
- 最適化する期間の設定
- パターン1:TVCM、Newspaper、Webのコストを最適化
- 最適化の実行
- (必要があれば)最適解の保存と読み込み
- 最適投資配分の最適化結果の出力
- パターン2:Newspaper、Webのコストを最適化
- 最適化の実行
- 最適投資配分の最適化結果の出力
- パターン3:TVCMのコストのみ最適化
- 最適化の実行
- 最適投資配分の最適化結果の出力
- まとめ
(前回と同じ)データセットと最適投資配分
今回利用するデータセット
以下のデータセットを利用します。
- 目的変数:売上金額(Sales)
- 説明変数:
- メディア:TVCM、Newspaper、Webのコスト
- イベント:XMas(クリスマス)フラグ(1: 12月25日、0: その他)
今回利用するデータセットは、以下からダウンロードできます。
MMM_xmas.csv
https://www.salesanalytics.co.jp/dcbd
今回は、以下のように設定しました。
- アドストックを考慮する:TVCM、Newspaper、Webのコスト
- アドストックを考慮しない:XMas(クリスマス)フラグ(1: 12月25日、0: その他)
今回構築するMMMと最適化
今回のMMM(マーケティングミックスモデリング)の予算最適化問題は、全体コスト一定の下で売上を最大化する、広告・販促の手段に対するコストの最適配分を求める問題になります。

MMMそのものが目的関数、MMMの出力である売上が目的変数になります。推定器にはRidge回帰を使います。
このRidge MMMパイプラインのハイパーパラメータは、Optunaで自動チューニングします。
特徴量は2つの視点で分けていきます。
- アドストックを考慮すべき特徴量 or そうでない特徴量
- アドストックを考慮する:TVCM、Newspaper、Webのコスト
- アドストックを考慮しない:XMas(クリスマス)フラグ(1: 12月25日、0: その他)
- 最適化対象となる特徴量 or そうではない特徴量
今回のケースですと、アドストックを考慮すべき特徴量=最適化対象となる特徴量ですが、必ずしもそうではありません。
そこで今回は、最適化対象となる特徴量を以下の3パターンを想定します。
- パターン1:TVCM、Newspaper、Webのコストを最適化
- パターン2:Newspaper、Webのコストを最適化
- パターン3:TVCMのコストのみ最適化
準備
モジュールの読み込み
先ず、必要なモジュールを読み込みます。
以下、コードです。
from mmm_functions5 import *
Pythonファイル(mmm_functions5.py)そのものは、以下からダウンロードできます。
mmm_functions5.py ※zipファイルを解凍してお使いください
https://www.salesanalytics.co.jp/uno8
mmm_functions5.pyには、MMMで共通して利用する処理を関数化したものや、クラス、モジュール類などを記載しています。前回作った最適化用の関数も含まれています。
mmm_functions5.pyを利用するときは、実行するPythonファイルやNotebookと同じフォルダに入れておいてください。
上手くいかないときは、mmm_functions5.pyをメモ帳などで開き内容をコピーし、実行するPythonファイルやNotebookにコードを張り付け、Pythonで関数を作ってからMMM構築などを行ってください。
データセットの読み込み
以下、コードです。
# データセット読み込み
dataset = 'https://www.salesanalytics.co.jp/dcbd'
df = pd.read_csv(
dataset,
parse_dates=['Week'],
index_col='Week',
)
# 説明変数Xと目的変数yに分解
X = df.drop(columns=['Sales'])
y = df['Sales']
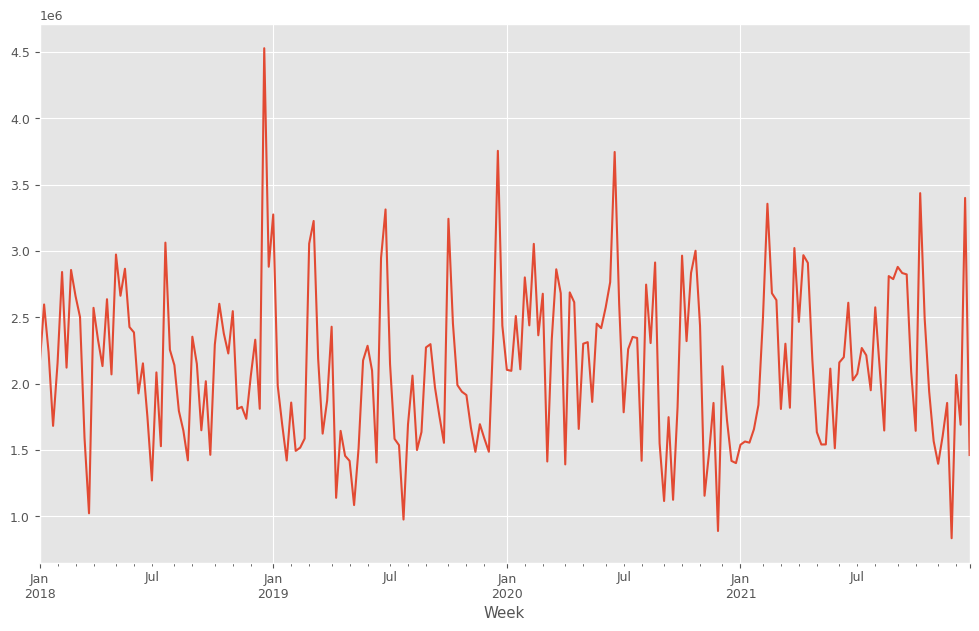
目的変数y(売上)をプロットします。
以下、コードです。
y.plot() plt.show()
以下、実行結果です。

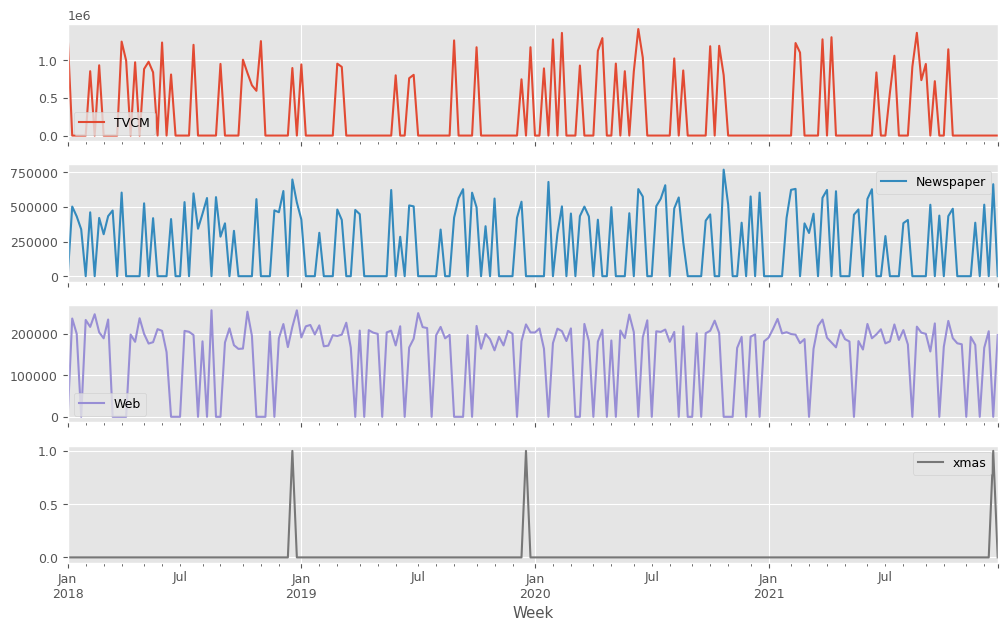
説明変数X(各メディアのコスト)をまとめてプロットします。
以下、コードです。
X.plot(subplots=True,figsize=(12,X.shape[1]*3)) plt.show()
以下、実行結果です。XMas変数は0-1変数(12月25日に1、その他の日は0)で、他の変数はコストデータです。

目的関数作り
今回の最適投資配分問題の目的関数は、Ridge MMMMパイプラインそのものになります。
アドストックを考慮する特徴量のリスト
先ず、アドストックを考慮する特徴量のリストを作ります。
以下、コードです。
# アドストックを考慮する特徴量のリストを作成 apply_effects_features = ['TVCM', 'Newspaper', 'Web']
最適なハイパーパラメータの探索
Ridge MMMパイプラインのハイパーパラメータをOptunaで探索します。
先ず、Optunaの目的関数を定義します。
以下、コードです。
#
# Optunaの目的関数
#
def ridge_objective_apply_effects(trial, X, y, apply_effects_features):
carryover_params = []
curve_params = []
# 列名リストからインデックスのリストを作成
apply_effects_indices = [X.columns.get_loc(column) for column in apply_effects_features]
no_effects_indices = list(set(range(X.shape[1])) - set(apply_effects_indices))
for feature in apply_effects_features:
carryover_length = trial.suggest_int(f'carryover_length_{feature}', 1, 10)
carryover_peak = trial.suggest_int(f'carryover_peak_{feature}', 1, carryover_length)
carryover_rate1 = trial.suggest_float(f'carryover_rate1_{feature}', 0, 1)
carryover_rate2 = trial.suggest_float(f'carryover_rate2_{feature}', 0, 1)
carryover_c1 = trial.suggest_float(f'carryover_c1_{feature}', 0, 2)
carryover_c2 = trial.suggest_float(f'carryover_c2_{feature}', 0, 2)
carryover_params.append({
'length': carryover_length,
'peak': carryover_peak,
'rate1': carryover_rate1,
'rate2': carryover_rate2,
'c1': carryover_c1,
'c2': carryover_c2,
})
saturation_function = trial.suggest_categorical(f'saturation_function_{feature}', ['logistic', 'exponential'])
if saturation_function == 'logistic':
curve_param_L = trial.suggest_float(f'curve_param_L_{feature}', 0, 10)
curve_param_k = trial.suggest_float(f'curve_param_k_{feature}', 0, 10)
curve_param_x0 = trial.suggest_float(f'curve_param_x0_{feature}', 0, 2)
curve_params.append({
'saturation_function': saturation_function,
'L': curve_param_L,
'k': curve_param_k,
'x0': curve_param_x0,
})
elif saturation_function == 'exponential':
curve_param_d = trial.suggest_float(f'curve_param_d_{feature}', 0, 10)
curve_params.append({
'saturation_function': saturation_function,
'd': curve_param_d,
})
alpha = trial.suggest_float('alpha', 1e-3, 1e+3)
preprocessor = ColumnTransformer(
transformers=[
('effects', Pipeline([
('carryover', CustomCarryOverTransformer(carryover_params=carryover_params)),
('saturation', CustomSaturationTransformer(curve_params=curve_params))
]), apply_effects_indices),
('no_effects', 'passthrough', no_effects_indices)
],
remainder='drop'
)
pipeline = Pipeline(steps=[
('scaler', MinMaxScaler()),
('preprocessor', preprocessor),
('ridge', Ridge(alpha=alpha))
])
tscv = TimeSeriesSplit(n_splits=5)
scores = cross_val_score(pipeline, X, y, cv=tscv, scoring='neg_mean_squared_error')
rmse = np.mean([np.sqrt(-score) for score in scores])
return rmse
この目的関数を使い、最適なハイパーパラメータを探索する関数を定義します。
以下、コードです。
#
# Optunaによる最適なハイパーパラメータの探索実行
#
def run_optimization(objective, X, y, apply_effects_features, n_trials=1000, study=None):
# Optunaのスタディの作成と最適化の実行
if study is None:
study = optuna.create_study(direction='minimize')
objective_with_data = partial(
objective,
X=X, y=y,
apply_effects_features=apply_effects_features)
study.optimize(
objective_with_data,
n_trials=n_trials,
show_progress_bar=True)
# 最適化の実行結果の表示
print("Best trial:")
trial = study.best_trial
print(f"Value: {trial.value}")
print("Params: ")
for key, value in trial.params.items():
print(f"{key}: {value}")
return study
この関数を実行し、最適なハイパーパラメータを探索します。
以下、コードです。
study = run_optimization(
ridge_objective_apply_effects,
X, y,
apply_effects_features,
n_trials=5000)
以下、実行結果です。
Best trial: 4501. Best value: 204788: 100%|██████████| 5000/5000 [41:54<00:00, 1.99it/s]Best trial: Value: 204788.44371312234 Params: carryover_length_TVCM: 4 carryover_peak_TVCM: 1 carryover_rate1_TVCM: 0.32819903336601947 carryover_rate2_TVCM: 0.4969553049890888 carryover_c1_TVCM: 0.6318981671828661 carryover_c2_TVCM: 0.9603003444386458 saturation_function_TVCM: exponential curve_param_d_TVCM: 1.5516303661805957 carryover_length_Newspaper: 2 carryover_peak_Newspaper: 1 carryover_rate1_Newspaper: 0.4535067838468354 carryover_rate2_Newspaper: 0.2975209559852316 carryover_c1_Newspaper: 1.1366865186930715 carryover_c2_Newspaper: 1.5685288408078186 saturation_function_Newspaper: logistic curve_param_L_Newspaper: 2.4563459432913817 curve_param_k_Newspaper: 3.4762655104119804 curve_param_x0_Newspaper: 0.5430944623066186 carryover_length_Web: 1 carryover_peak_Web: 1 carryover_rate1_Web: 0.893393586575752 carryover_rate2_Web: 0.015127230086579003 carryover_c1_Web: 0.6965309047325878 carryover_c2_Web: 1.4187849854952554 saturation_function_Web: exponential curve_param_d_Web: 5.218876060554834 alpha: 0.017681897520184946
(必要があれば)Optunaのstudyの保存と読み込み
Optunaのハイパーパラメータの探索は時間が掛かります。
その探索結果などが格納されているstudyを保存したり、保存したstudyを読み込みハイパーパラメータをさらに探索することができます。
以下は、optunaのstudyの保存する場合のコードです。
# optunaのstudyの保存 joblib.dump(study, 'ridgeMMM_study.joblib')
以下は、optunaの保存してあったstudyを読み込み、再度最適化の実行するときのコードです。
#
# 保存されたstudyを使い最適化の実行
#
# 保存されたstudyを読み込む
study = joblib.load('ridgeMMM_study.joblib')
# 読み込んだstudyをもとにOptunaによる最適なハイパーパラメータの探索実行
study = run_optimization(
ridge_objective_apply_effects,
X, y,
apply_effects_features,
n_trials=50,
study=study)
念のため、保存しておくことをお勧めします。
MMMパイプラインの構築
Optunaで探索し見つけたハイパーパラメータを取得し、Ridge MMMパイプラインを構築します。
そのための関数を定義します。
以下、コードです。
def create_model_from_trial_ridge(trial, X, y, apply_effects_features):
#
# Optunaの実行結果からハイパーパラメータを取得
#
carryover_keys = ['length', 'peak', 'rate1', 'rate2', 'c1', 'c2']
curve_keys_logistic = ['L', 'k', 'x0']
curve_keys_exponential = ['d']
# ハイパーパラメータを抽出しキーと値の辞書を作成
def fetch_params(prefix, feature_name, params, trial_params):
return {key: trial_params[f'{prefix}_{key}_{feature_name}'] for key in params}
# キャリーオーバー効果関数ハイパーパラメータを抽出
carryover_params = [fetch_params('carryover', feature_name, carryover_keys, trial.params) for feature_name in apply_effects_features]
# 飽和関数ハイパーパラメータを抽出
curve_params = []
for feature_name in apply_effects_features:
saturation_function = trial.params[f'saturation_function_{feature_name}']
curve_param = {'saturation_function': saturation_function}
if saturation_function == 'logistic':
curve_param.update(fetch_params('curve_param', feature_name, curve_keys_logistic, trial.params))
elif saturation_function == 'exponential':
curve_param.update(fetch_params('curve_param', feature_name, curve_keys_exponential, trial.params))
curve_params.append(curve_param)
# 推定器ハイパーパラメータを抽出
alpha = trial.params['alpha']
#
# MMMパイプラインの構築&学習
#
MMM_pipeline, trained_model, pred = build_MMM_pipeline_ridge(
X, y,
apply_effects_features,
carryover_params,
curve_params,
alpha)
# 最適ハイパーパラメータの集約
model_params = [
carryover_params,
curve_params,
alpha]
return trained_model,model_params
戻り値のtrained_modelが学習済みのRidge MMMパイプラインで、model_paramsがそのハイパーパラメータです。
では、この関数を実行します。
以下、コードです。
trained_model,model_params = create_model_from_trial_ridge(
study.best_trial,
X, y,
apply_effects_features)
以下、実行結果です。
RMSE: 166823.76823520425 MAE: 132263.27703129503 MAPE: 0.06663822033219063 R2: 0.9222550584365593
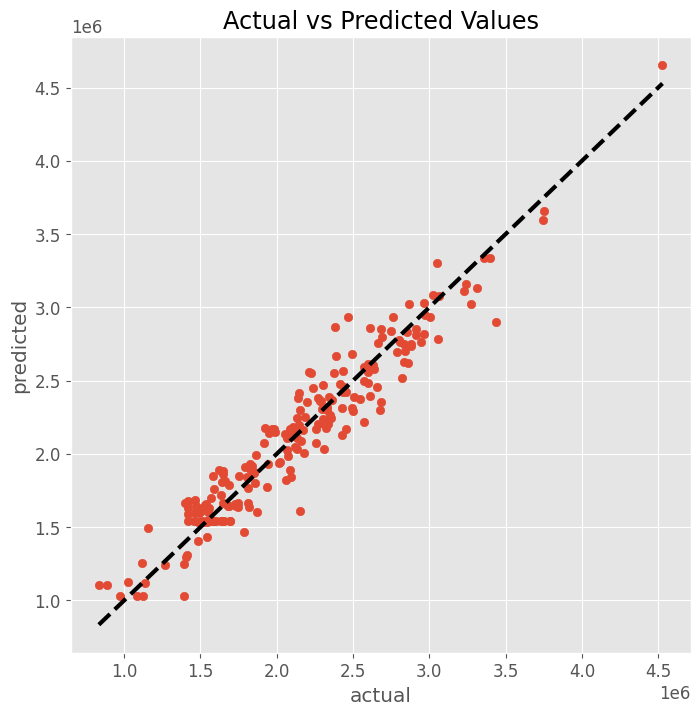
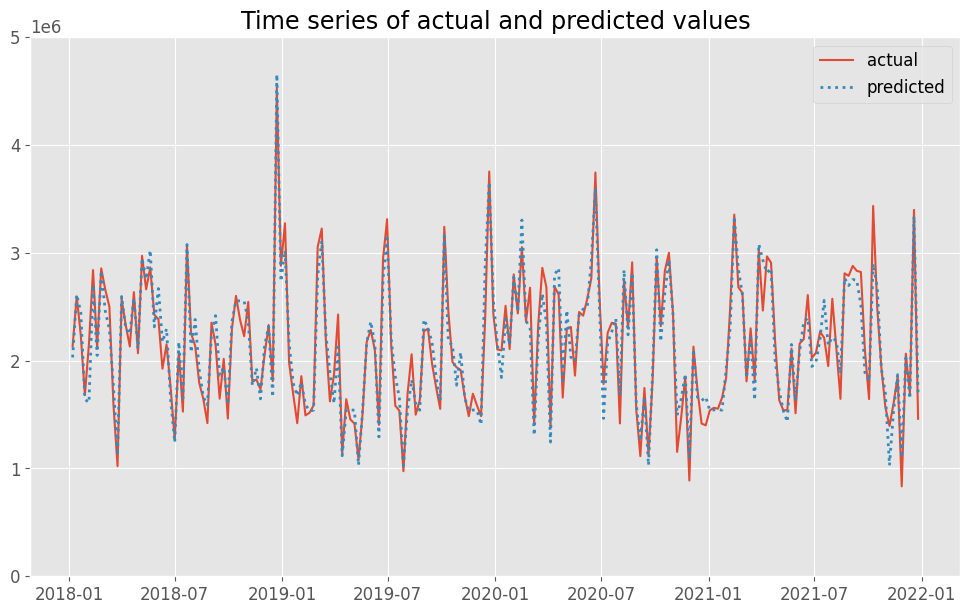
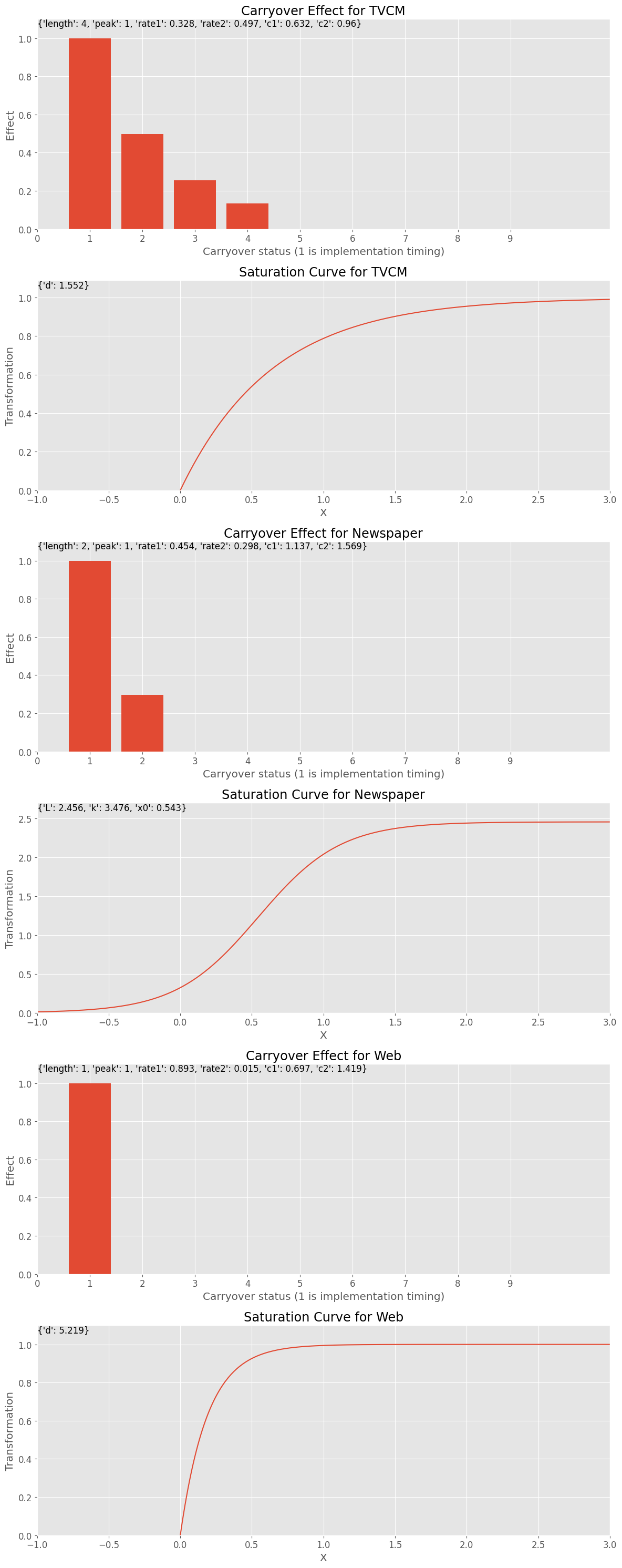
アドストックの状況をグラフで確認します。
以下、コードです。
# グラフで確認
best_carryover_params = model_params[0]
best_curve_params = model_params[1]
plot_effects(
best_carryover_params,
best_curve_params,
apply_effects_features)
以下、実行結果です。
(必要があれば)学習済みモデルの保存と読み込み
必要があれば、学習済みのMMMパイプラインを外部ファイル(joblib形式)として保存しておくといいでしょう。
以下、コードです。
# 学習済みモデルtrained_modelを外部ファイルとして保存する model_path = 'ridgeMMM_trained_model.joblib' joblib.dump(trained_model, model_path)
外部ファイル(joblib形式)として保存した学習済みのMMMパイプラインを読み込むとき、以下のコードで実施します。
以下、コードです。
# 外部ファイル(学習済みモデル)を読み込む model_path = 'ridgeMMM_trained_model.joblib' trained_model = joblib.load(model_path)
売上貢献度とマーケティングROI
このMMMパイプラインから、売上貢献度やマーケティングROIなどを求めていきます。
先ずは、貢献度の推移です。
以下、コードです。
# 貢献度の算出 contribution = calculate_and_plot_contribution(y, X, trained_model,(0, 5e6)) print(contribution)
以下、実行結果です。
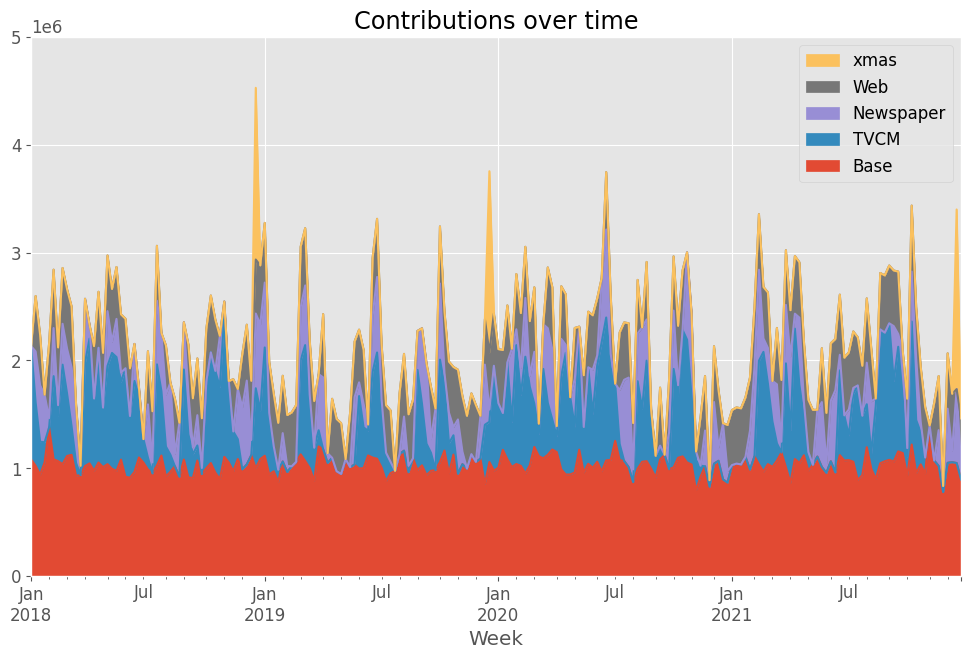
Base TVCM Newspaper Web \
Week
2018-01-07 1.080521e+06 1.051479e+06 0.000000 0.000000
2018-01-14 1.021997e+06 5.881997e+05 472301.737648 513601.745299
2018-01-21 9.399495e+05 3.047772e+05 523392.421779 468080.933370
2018-01-28 1.052595e+06 1.869167e+05 441387.833033 0.000000
2018-02-04 1.377201e+06 0.000000e+00 86495.001993 691704.166803
... ... ... ... ...
2021-11-28 7.772009e+05 0.000000e+00 56699.132728 0.000000
2021-12-05 1.049066e+06 0.000000e+00 502174.282635 513459.505109
2021-12-12 1.055146e+06 0.000000e+00 107858.694624 526495.595001
2021-12-19 1.047147e+06 0.000000e+00 685176.579736 0.000000
2021-12-26 8.932214e+05 0.000000e+00 123553.559520 444325.026272
xmas
Week
2018-01-07 0.000000e+00
2018-01-14 0.000000e+00
2018-01-21 0.000000e+00
2018-01-28 0.000000e+00
2018-02-04 0.000000e+00
... ...
2021-11-28 0.000000e+00
2021-12-05 0.000000e+00
2021-12-12 0.000000e+00
2021-12-19 1.666877e+06
2021-12-26 0.000000e+00
[208 rows x 5 columns]
次に、貢献度の構成比を求めます。
以下、コードです。
# 貢献度構成比の算出 contribution_results = summarize_and_plot_contribution(contribution) print(contribution_results)
以下、実行結果です。
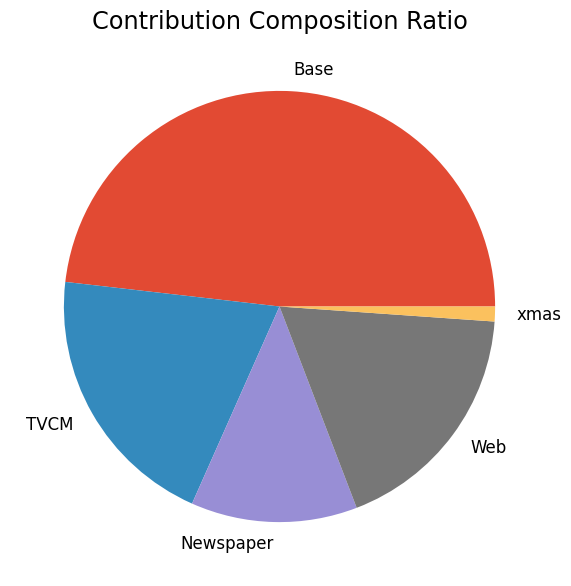
contribution ratio Base 2.140160e+08 0.481805 TVCM 8.960626e+07 0.201727 Newspaper 5.540727e+07 0.124736 Web 8.022569e+07 0.180608 xmas 4.941457e+06 0.011124
売上貢献度とコストから、マーケティングROIを求めます。
以下、コードです。
# マーケティングROIの算出
ROI = calculate_marketing_roi(
X[apply_effects_features],
contribution[apply_effects_features]
)
# 数値を表示
print(ROI)
以下、実行結果です。
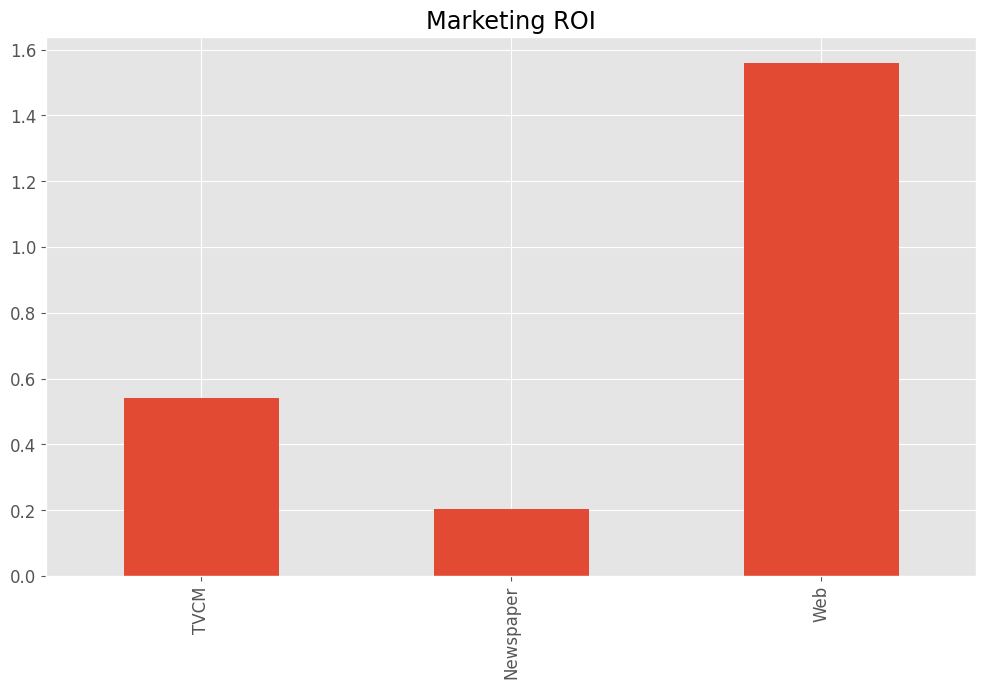
TVCM 0.541017 Newspaper 0.204867 Web 1.560724 dtype: float64
売上貢献度(横軸)×マーケティングROI(縦軸)のマップを描きます。円の大きさはコストを表します。
以下、コードです。
# 散布図作成(売上貢献度×マーケティングROI)
data_to_plot = plot_scatter_of_contribution_and_roi(
X[apply_effects_features],
contribution[apply_effects_features]
)
# 散布図の数値を表示
print(data_to_plot)
以下、実行結果です。
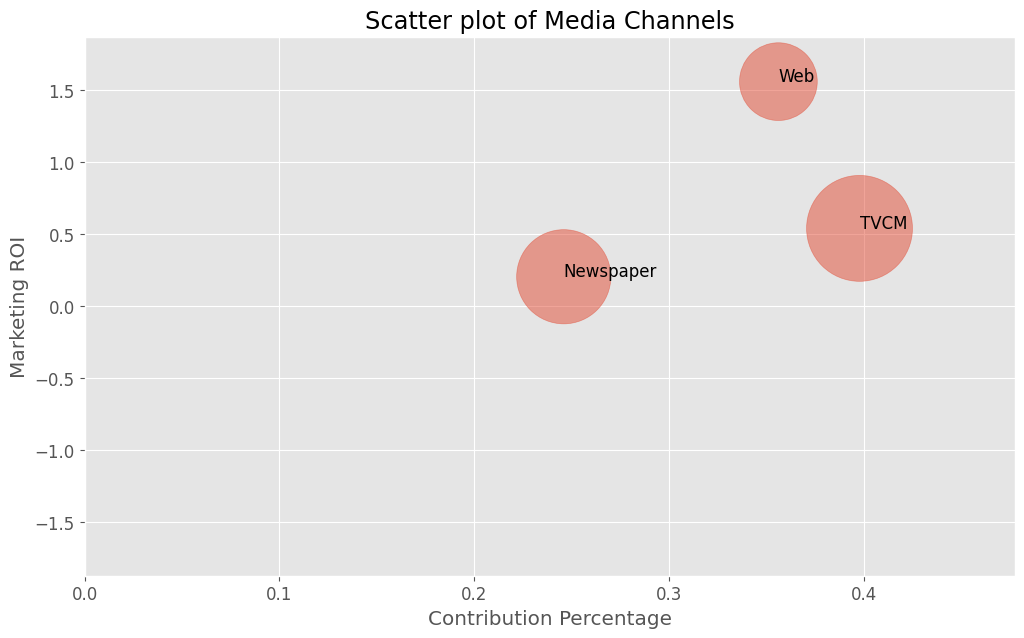
contribution_percentage ROI cost TVCM 0.397827 0.541017 58147500 Newspaper 0.245993 0.204867 45986200 Web 0.356180 1.560724 31329300
最適投資配分
構築したRidge MMMMパイプラインを最大化する最適投資配分問題を解き、広告・販促のコストの最適投資配分を求めます。
最後に、現状と最適化後の結果を比較し、どのような変化が起こるかを出力します。
最適化する期間の設定
最適化する期間は、直近1年間(52週間)です。
以下、コードです。
# 最適化期間を表す変数、ここでは直近1年間(52週間)を指定 term = 52 # 最適化期間における対象特徴量Xのデータを抽出 X_actual = X[-term:] # 最適化期間における目的変数yのデータを抽出 y_actual = y[-term:]
今回は、最適化対象となる特徴量を以下の3パターンを想定します。
- パターン1:TVCM、Newspaper、Webのコストを最適化
- パターン2:Newspaper、Webのコストを最適化
- パターン3:TVCMのコストのみ最適化
パターン1:TVCM、Newspaper、Webのコストを最適化
以下を最適対象の特徴量とします。
- TVCM:最適対象の特徴量
- Newspaper:最適対象の特徴量
- Web:最適対象の特徴量
以下、コードです。
# 最適化対象の特徴量のリストを作成 optimized_features = ['TVCM', 'Newspaper', 'Web']
最適化の実行
MMMパイプラインの出力である売上を全体コスト一定(現在のコストを合計した値)のもとで最大化する、非線形最適問題を定義し、最適解を求めます。
以下、コードです。
#
# 最適投資配分
#
opt_results = optimize_investment(
trained_model,
X_actual,
optimized_features,
niter = 100)
最適化の計算が終了したら、その最適解を取得します。
以下、コードです。
# # 最適解の取得 # X_optimized = opt_results['X_optimized'] # 最適化後の特徴量を表示 print(X_optimized)
以下、実行結果です。
TVCM Newspaper Web xmas Week 2021-01-03 386109.709759 1396.048701 114409.813596 0 2021-01-10 368747.070430 1046.365404 122764.200664 0 2021-01-17 199335.743966 27582.927177 120114.326286 0 2021-01-24 680289.895220 0.000100 99540.388782 0 2021-01-31 141089.740497 434412.513033 111025.907257 0 2021-02-07 30560.886451 639621.878164 104567.873456 0 2021-02-14 523573.876952 411604.439283 108730.488319 0 2021-02-21 561833.091365 236726.146332 100822.532452 0 2021-02-28 116926.987898 439290.683694 135342.011145 0 2021-03-07 115723.361772 29709.757199 106787.063994 0 2021-03-14 337817.364044 443.129734 115503.631931 0 2021-03-21 243955.340059 76195.984534 118283.895938 0 2021-03-28 546453.955700 736558.706184 105643.919636 0 2021-04-04 110373.913474 180644.549527 100347.140411 0 2021-04-11 865680.399831 3484.359591 95752.733826 0 2021-04-18 143331.897594 12977.662990 97681.243961 0 2021-04-25 330855.256465 4269.937355 109647.418286 0 2021-05-02 164865.054702 0.000193 117886.458028 0 2021-05-09 494951.184328 24028.502011 93200.463905 0 2021-05-16 302342.840453 704268.607161 119215.579769 0 2021-05-23 406217.812107 484336.459130 109890.339151 0 2021-05-30 383899.180243 29862.939291 101752.035487 0 2021-06-06 461699.843831 164693.322685 97189.642346 0 2021-06-13 312277.182816 462501.892020 100342.476269 0 2021-06-20 431481.242431 1383.053848 93385.623661 0 2021-06-27 352889.832110 10302.154141 102202.218650 0 2021-07-04 21066.645959 10.067654 128588.358409 0 2021-07-11 617971.836328 16327.591968 109074.989271 0 2021-07-18 702380.633923 1479.181054 98632.783503 0 2021-07-25 154060.721060 998313.635555 106333.441821 0 2021-08-01 47371.851620 347230.823188 109876.465995 0 2021-08-08 257769.450829 22693.005676 100783.471344 0 2021-08-15 698952.170867 5378.367165 122894.438093 0 2021-08-22 676769.332394 2148.705553 109902.044558 0 2021-08-29 49824.631769 1645.584217 106816.352656 0 2021-09-05 931694.692335 54313.382991 112663.128617 0 2021-09-12 203102.920604 493929.994842 111002.708947 0 2021-09-19 349250.067937 366950.723146 115193.964633 0 2021-09-26 240012.253004 499077.783019 116368.361687 0 2021-10-03 256060.602943 362831.614928 97262.712872 0 2021-10-10 496012.718807 10.066864 106703.059162 0 2021-10-17 99629.545409 680462.052545 110738.752036 0 2021-10-24 146891.849200 15.170111 113006.703606 0 2021-10-31 322345.499886 986.622633 100788.741676 0 2021-11-07 257109.964537 5584.171434 106454.084482 0 2021-11-14 412875.109144 43597.932421 93308.710199 0 2021-11-21 370524.826274 9305.213550 114264.747758 0 2021-11-28 383033.275884 256.199290 101272.382577 0 2021-12-05 478450.712673 667936.738247 95021.249495 0 2021-12-12 414391.846600 7543.397928 110764.766109 0 2021-12-19 67710.005742 213699.391946 91827.478422 1 2021-12-26 0.000017 1441.236068 111770.171150 0
(必要があれば)最適解の保存と読み込み
必要があれば、最適解を保存しておきましょう。通常のPandasのデータフレームの保存です。
以下、コードです。
# (必要があれば)最適解の保存 X_optimized_path = 'X_optimized.csv' X_optimized.to_csv(X_optimized_path)
保存したファイルを読み込むときは、以下です。
#(必要があれば)最適解の読み込み X_optimized_path = 'X_optimized.csv' X_optimized = pd.read_csv(X_optimized_path, index_col=0)
最適投資配分の最適化結果の出力
現状と最適化の結果を比較していきます。
先ずは、売上金額とマーケティングROIです。
以下、コードです。
#
# 現状と最適配分時の比較(yとマーケティングROI)
#
result = compare_y_and_marketing_roi(
X_optimized,
X_actual,
y_actual,
trained_model,
apply_effects_features)
# 数値の表示
for key,value in result.items():
print(f"{key}: {value}")
以下、実行結果です。
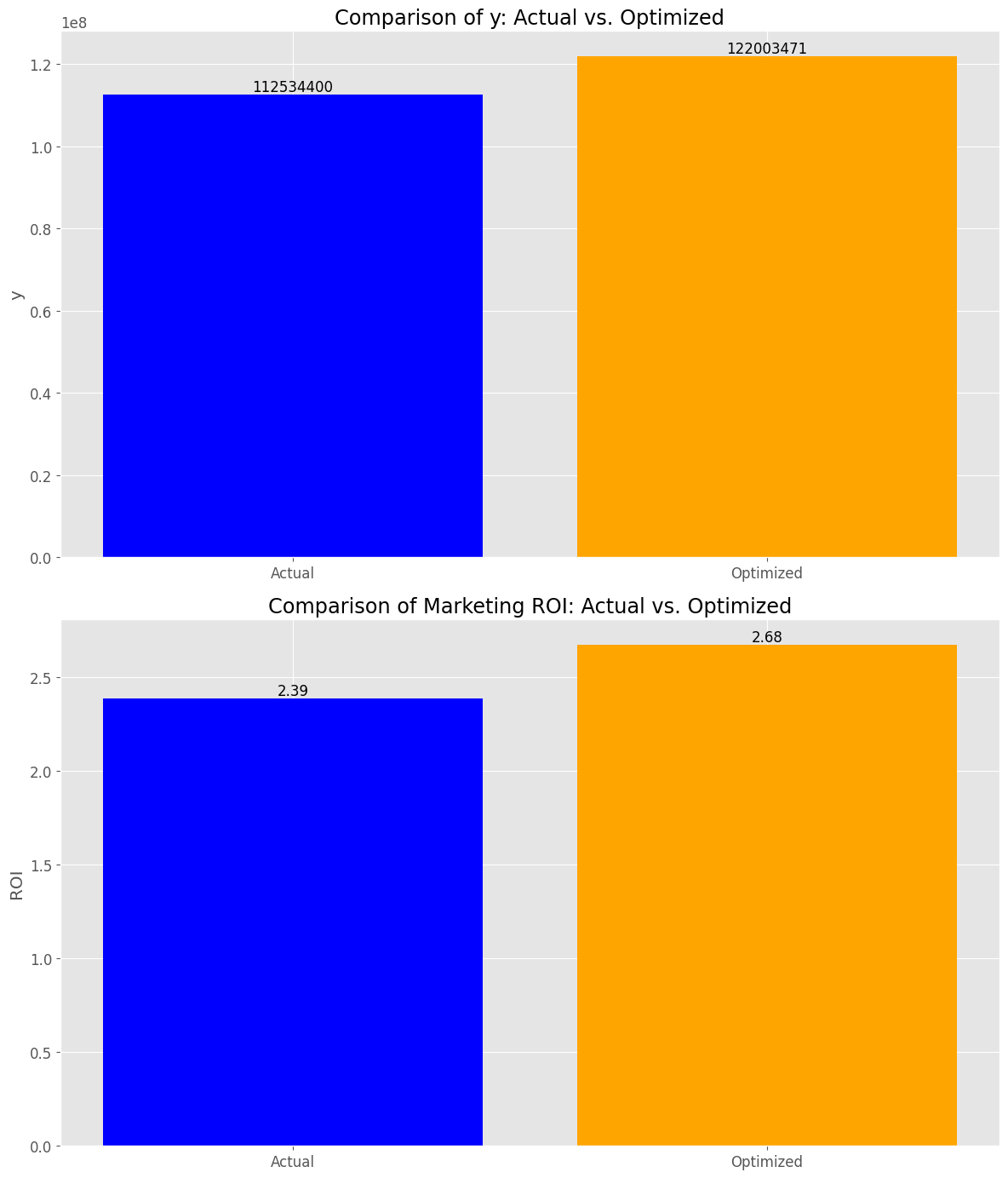
y_actual_sum: 112534400 y_optimized_sum: 122003471 y_change_percent: +8.41 % roi_actual: 2.39 roi_optimized: 2.68 roi_change_point: +0.29 points
次に、投資配分です。
以下、コードです。
#
# 投資配分構成比の比較
#
comparison_df = plot_comparative_allocation(
X_actual,
X_optimized,
apply_effects_features)
# 数値の表示
print(comparison_df)
以下、実行結果です。
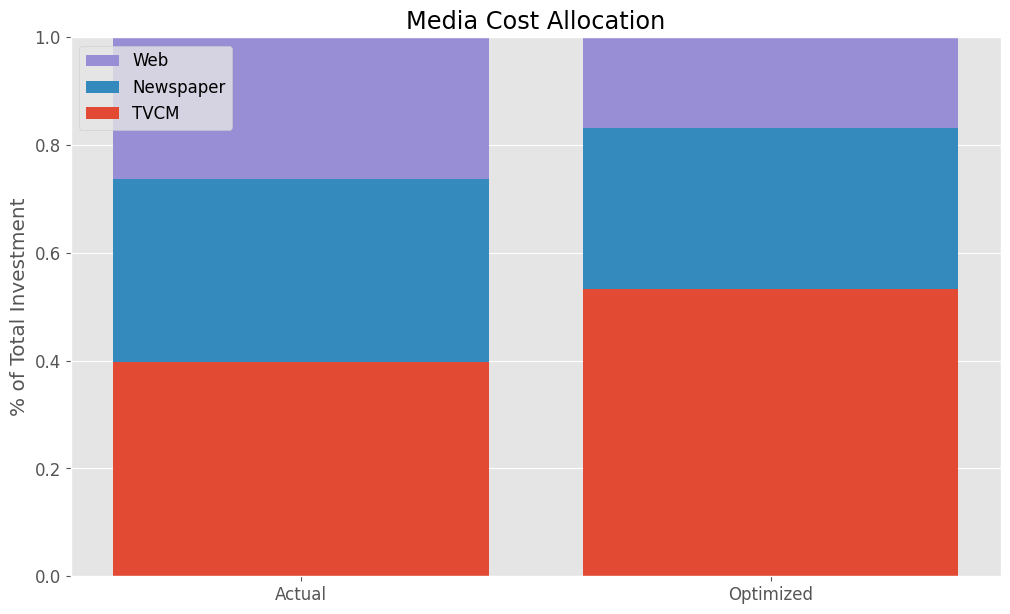
Actual Allocation Optimized Allocation TVCM 0.397076 0.532307 Newspaper 0.339156 0.298879 Web 0.263768 0.168814
パターン2:Newspaper、Webのコストを最適化
以下を最適対象の特徴量とします。
- TVCM:最適対象外
- Newspaper:最適対象の特徴量
- Web:最適対象の特徴量
以下、コードです。
# 最適化対象の特徴量のリストを作成 optimized_features = ['Newspaper', 'Web']
最適化の実行
MMMパイプラインの出力である売上を全体コスト一定(現在のコストを合計した値)のもとで最大化する、非線形最適問題を定義し、最適解を求めます。
以下、コードです。
#
# 最適投資配分
#
opt_results = optimize_investment(
trained_model,
X_actual,
optimized_features,
niter = 100)
最適化の計算が終了したら、その最適解を取得します。
以下、コードです。
# # 最適解の取得 # X_optimized = opt_results['X_optimized'] # 最適化後の特徴量を表示 print(X_optimized)
以下、実行結果です。TVCMの特徴量の値が変わっていないことが確認できます。
TVCM Newspaper Web xmas Week 2021-01-03 0 508.864503 99255.751765 0 2021-01-10 0 242.000410 102226.196677 0 2021-01-17 0 682.035291 101034.421565 0 2021-01-24 0 3843.639729 106085.746920 0 2021-01-31 0 498928.295939 83945.521462 0 2021-02-07 0 323022.353990 140843.871095 0 2021-02-14 1225600 503217.898205 99271.467935 0 2021-02-21 1098900 349812.305820 99935.937785 0 2021-02-28 0 448198.774896 108546.825550 0 2021-03-07 0 749032.738312 116116.369312 0 2021-03-14 0 407088.701786 100758.846343 0 2021-03-21 0 57668.666371 109521.437520 0 2021-03-28 1274700 832005.722858 90220.827473 0 2021-04-04 0 319191.447310 85479.779290 0 2021-04-11 1302600 36265.560945 105026.935194 0 2021-04-18 0 746331.622358 118541.115534 0 2021-04-25 0 9825.330670 108285.019479 0 2021-05-02 0 3367.458697 138544.297153 0 2021-05-09 0 150955.462951 119340.122980 0 2021-05-16 0 675617.412301 97605.752468 0 2021-05-23 0 524182.279637 100278.426542 0 2021-05-30 0 458544.221528 83688.813786 0 2021-06-06 0 698538.413072 107323.696112 0 2021-06-13 0 343183.607982 123796.602021 0 2021-06-20 836300 226176.984401 110142.546931 0 2021-06-27 0 396966.959513 98088.356360 0 2021-07-04 0 527546.988277 106098.560537 0 2021-07-11 566400 48224.301183 131959.119776 0 2021-07-18 1057500 4588.457027 97128.312835 0 2021-07-25 0 7744.027404 81608.587457 0 2021-08-01 0 321688.444856 93628.410264 0 2021-08-08 0 7296.467629 112841.393170 0 2021-08-15 911700 8200.678291 112771.641193 0 2021-08-22 1360900 36690.226008 112682.840133 0 2021-08-29 734000 6654.442655 102195.516629 0 2021-09-05 948100 2911.016455 95800.931710 0 2021-09-12 0 794572.349171 88721.244998 0 2021-09-19 720400 359148.276131 127101.542993 0 2021-09-26 0 555571.775013 122486.662127 0 2021-10-03 0 42373.864699 110524.004753 0 2021-10-10 1142800 730586.784640 104667.967797 0 2021-10-17 0 487733.551897 92107.107100 0 2021-10-24 0 0.000000 105193.350239 0 2021-10-31 0 1146.906149 101723.435382 0 2021-11-07 0 5528.402330 119171.669595 0 2021-11-14 0 2229.745246 127170.273329 0 2021-11-21 0 3003.816233 107508.408307 0 2021-11-28 0 310835.526919 120973.985296 0 2021-12-05 0 609639.748157 114783.231211 0 2021-12-12 0 132803.162434 96762.730626 0 2021-12-19 0 676073.622918 112874.572104 1 2021-12-26 0 84.102961 113834.371033 0
最適投資配分の最適化結果の出力
現状と最適化の結果を比較していきます。
先ずは、売上金額とマーケティングROIです。
以下、コードです。
#
# 現状と最適配分時の比較(yとマーケティングROI)
#
result = compare_y_and_marketing_roi(
X_optimized,
X_actual,
y_actual,
trained_model,
apply_effects_features)
# 数値の表示
for key,value in result.items():
print(f"{key}: {value}")
以下、実行結果です。
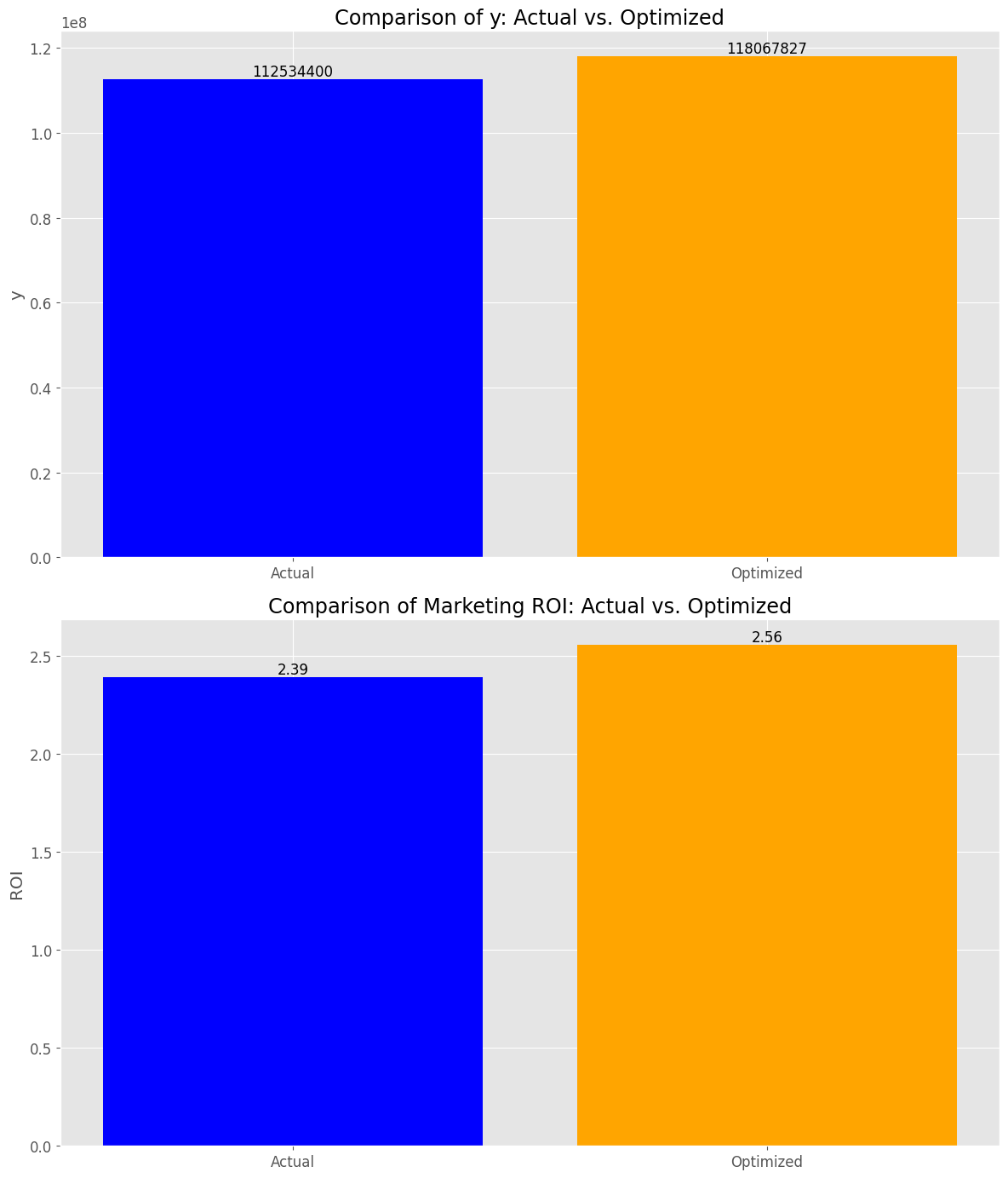
y_actual_sum: 112534400 y_optimized_sum: 118067827 y_change_percent: +4.92 % roi_actual: 2.39 roi_optimized: 2.56 roi_change_point: +0.17 points
次に、投資配分です。
以下、コードです。
#
# 投資配分構成比の比較
#
comparison_df = plot_comparative_allocation(
X_actual,
X_optimized,
apply_effects_features)
# 数値の表示
print(comparison_df)
以下、実行結果です。
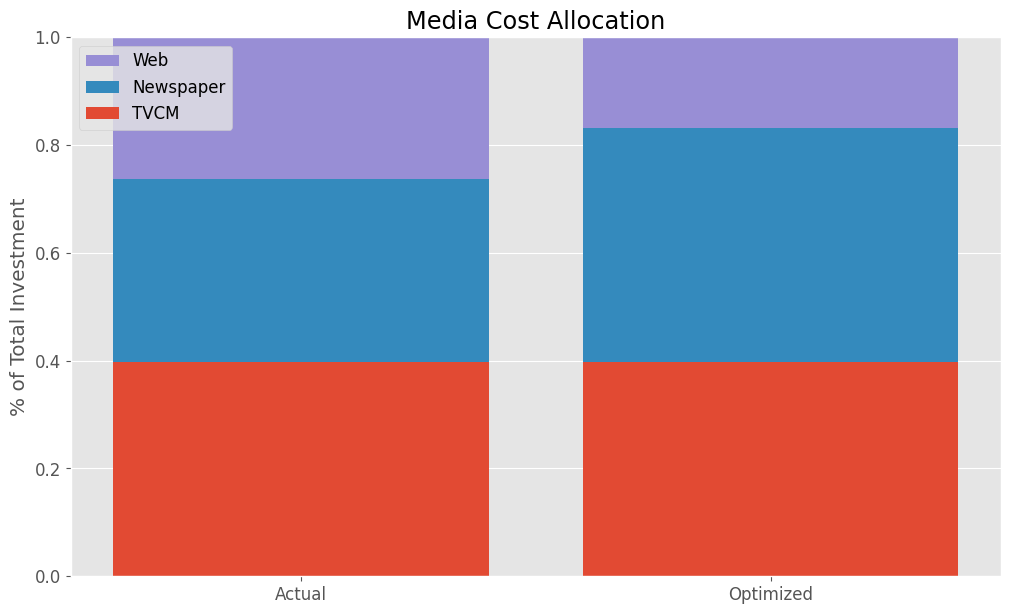
Actual Allocation Optimized Allocation TVCM 0.397076 0.397076 Newspaper 0.339156 0.435228 Web 0.263768 0.167696
TVCMの割合だけ変化していないことが分かります。
パターン3:TVCMのコストのみ最適化
以下を最適対象の特徴量とします。
- TVCM:最適対象の特徴量
- Newspaper:最適対象外
- Web:最適対象外
以下、コードです。
# 最適化対象の特徴量のリストを作成 optimized_features = ['TVCM']
最適化の実行
MMMパイプラインの出力である売上を全体コスト一定(現在のコストを合計した値)のもとで最大化する、非線形最適問題を定義し、最適解を求めます。
以下、コードです。
#
# 最適投資配分
#
opt_results = optimize_investment(
trained_model,
X_actual,
optimized_features,
niter = 100)
最適化の計算が終了したら、その最適解を取得します。
以下、コードです。
# # 最適解の取得 # X_optimized = opt_results['X_optimized'] # 最適化後の特徴量を表示 print(X_optimized)
以下、実行結果です。TVCMのみ変化しています。
TVCM Newspaper Web xmas Week 2021-01-03 385212.523540 0 191200 0 2021-01-10 160493.747565 0 212500 0 2021-01-17 351781.226165 0 236500 0 2021-01-24 238920.908995 0 201400 0 2021-01-31 259530.097812 420300 204400 0 2021-02-07 262138.577031 623800 200000 0 2021-02-14 383455.452634 630800 198400 0 2021-02-21 254290.336840 0 177900 0 2021-02-28 189904.625892 381500 187800 0 2021-03-07 126433.823696 312200 0 0 2021-03-14 265226.742118 451400 164000 0 2021-03-21 216903.259045 0 219500 0 2021-03-28 333261.479156 566400 234900 0 2021-04-04 165784.529309 622900 191100 0 2021-04-11 465672.424203 0 179600 0 2021-04-18 242570.130262 613600 167800 0 2021-04-25 272384.950885 0 209700 0 2021-05-02 143809.037169 0 187700 0 2021-05-09 251258.257899 0 181900 0 2021-05-16 198640.887279 444000 0 0 2021-05-23 587918.593877 482300 182900 0 2021-05-30 84785.693521 0 162500 0 2021-06-06 102963.834106 558100 224300 0 2021-06-13 443981.440325 628400 189700 0 2021-06-20 236054.470058 0 199200 0 2021-06-27 168743.087625 0 211400 0 2021-07-04 268016.626978 289800 177400 0 2021-07-11 246387.735580 0 182200 0 2021-07-18 318307.864063 0 223100 0 2021-07-25 270123.745739 0 185700 0 2021-08-01 321689.023317 383200 209500 0 2021-08-08 206196.828542 406100 174800 0 2021-08-15 315720.477855 0 0 0 2021-08-22 233948.378874 0 217800 0 2021-08-29 17068.750560 0 203300 0 2021-09-05 445065.417387 0 200400 0 2021-09-12 366835.763649 516100 157800 0 2021-09-19 119261.796796 0 225600 0 2021-09-26 245043.742374 437700 0 0 2021-10-03 246328.326017 0 169200 0 2021-10-10 290801.974924 433800 231700 0 2021-10-17 248594.704368 487500 190000 0 2021-10-24 315236.594133 0 177600 0 2021-10-31 347843.046176 0 175200 0 2021-11-07 220100.709087 0 0 0 2021-11-14 205520.303338 0 192800 0 2021-11-21 276653.045069 386300 173700 0 2021-11-28 231562.556755 0 0 0 2021-12-05 262974.999643 516700 166800 0 2021-12-12 361665.199177 0 206600 0 2021-12-19 623.027726 664500 0 1 2021-12-26 6209.224867 0 197600 0
最適投資配分の最適化結果の出力
現状と最適化の結果を比較していきます。
先ずは、売上金額とマーケティングROIです。
以下、コードです。
#
# 現状と最適配分時の比較(yとマーケティングROI)
#
result = compare_y_and_marketing_roi(
X_optimized,
X_actual,
y_actual,
trained_model,
apply_effects_features)
# 数値の表示
for key,value in result.items():
print(f"{key}: {value}")
以下、実行結果です。
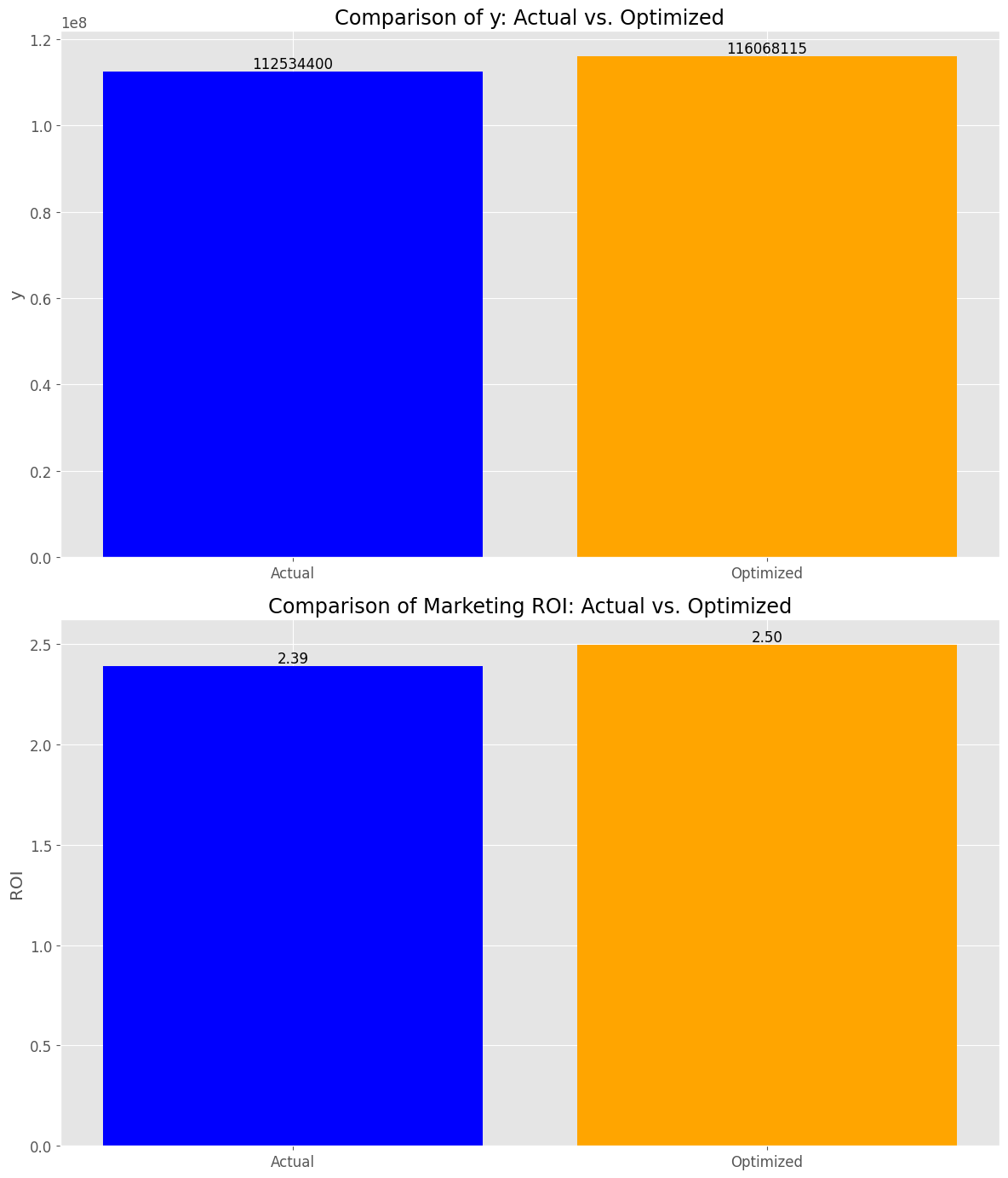
y_actual_sum: 112534400 y_optimized_sum: 116068115 y_change_percent: +3.14 % roi_actual: 2.39 roi_optimized: 2.50 roi_change_point: +0.11 points
次に、投資配分です。
以下、コードです。
#
# 投資配分構成比の比較
#
comparison_df = plot_comparative_allocation(
X_actual,
X_optimized,
apply_effects_features)
# 数値の表示
print(comparison_df)
以下、実行結果です。
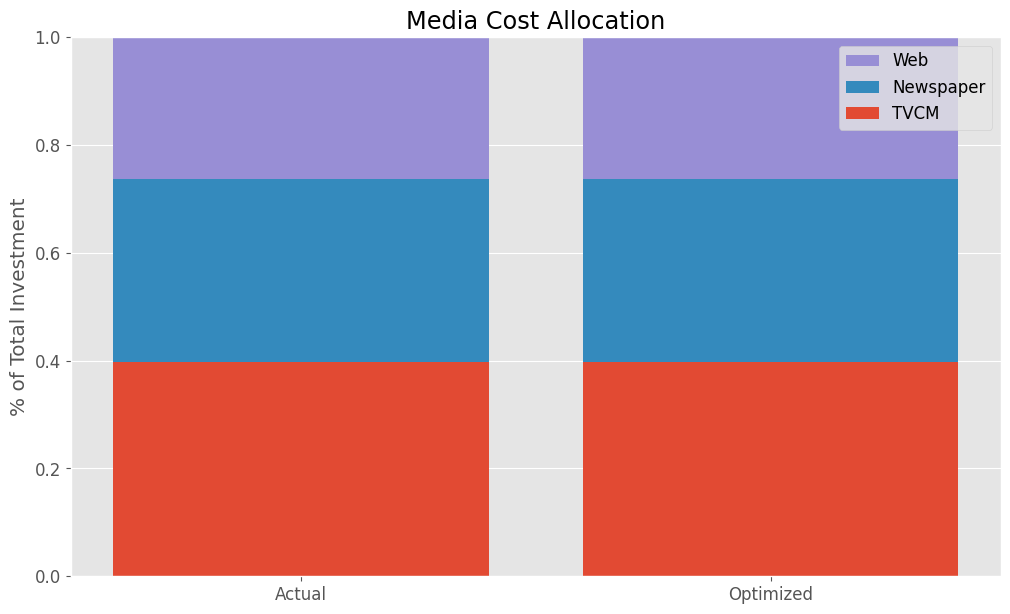
Actual Allocation Optimized Allocation TVCM 0.397076 0.397076 Newspaper 0.339156 0.339156 Web 0.263768 0.263768
集計値のため構成比に変化はありません。先ほど見た通り、TVCMの詳細を見ると異なってきます。
まとめ
今回は、「Ridge MMMパイプラインのハイパーパラメータをOptunaで最適化し、アドストックを考慮すべきどうか、コスト最適化の対象かどうか、特徴量を指定し構築する線形回帰系MMM」のお話しをしました。
MMMの最適投資配分の問題は、非線形計画問題のため、得られた解が大域的最適解ではなく局所的最適解に陥ることがあります。
ちなみに、大域的最適解は、探索空間全体において目的関数の最適値(最大値または最小値)を与える解のことです。要するに、本当の最適解のことです。
一方、局所的最適解というのがあります。
局所的最適解とは、この解の近傍においてのみ目的関数が最適値をとる解であり、必ずしも大域的な最適解とは限りません。つまり、探索範囲全体を見渡せば、さらに良い解が存在する可能性があります。
多くの最適化手法は、局所的な最適解に陥りやすいため、大域的最適解を得るためには、特別な工夫が必要となります。
たとえば、局所最適解をすべて探し出し、その中でも最も良い局所最適解は大域最適解です。
ただし、そのような方法は膨大な時間が掛かるため、工夫が必要になってきます。
今回までは、そのような工夫をScipyの最適化の機能で実施していましたが、十分ではない可能性があります。
別の機会に、Scipy以外のライブラリーを使い、大域的最適解を得るための手段を紹介します。
次回は、季節性などを考慮する方法を説明します。

