【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！

– 【第1回】非線形計画問題と大域的最適化の基礎 –

4068
【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！– 【第1回】非線形計画問題と大域的最適化の基礎 –

最適化問題は、工学、経済学、物理学など様々な分野で登場します。機械学習のハイパーパラメータチューニング、構造設計の最適化、リソース配分の最適化など、最適な解を求めることは、多くの問題解決に不可欠です。

最適化問題の中でも、特に非線形計画問題は現実世界の複雑な問題を表現するのに適しています。

非線形計画問題は実社会のさまざまな分野で応用されています。

例えば、スマホアプリの経路検索や電車の乗り換え検索などの身近なものから、宇宙開発や核融合研究などの最新のもの、さらには機械学習の根幹にかかわる学習（実際は何かしら最適化を行っている）まで、人類にとってなくてはならないものです。

ここで、いくつか代表的な例を挙げます。

分野 適用例
マーケティング 価格最適化, 広告予算配分の最適化, など
営業 営業担当の割り当て最適化, クロスセリング戦略の最適化, など
生産 生産計画の最適化, 設備のメンテナンススケジューリング, 品質管理パラメータの最適化, など
サプライチェーン サプライチェーンネットワーク設計, 在庫配置の最適化, 調達計画の最適化, など
人事 人員配置の最適化, シフトスケジューリング, 人材育成計画の最適化, など
ファイナンス ポートフォリオ最適化, オプション価格決定, 年金運用の最適化, など
エネルギー 電力システムの最適化, ガスパイプラインの最適運用, 石油化学プラントの最適運転, など
水資源管理 ダムの放流量最適化, 地下水揚水の最適化, 上下水道ネットワークの最適設計, など
機械学習 サポートベクターマシンの学習, ニューラルネットワークの学習, ロジスティック回帰の学習, など
構造設計 トラス構造の最適設計, 板厚の最適設計, 形状最適設計, など
輸送・ロジスティクス 輸送ネットワークの設計, 配送ルートの最適化, 在庫管理の最適化, など
通信ネットワーク 通信ネットワークの最適設計, 周波数割り当ての最適化, 送信電力の最適制御, など
画像・信号処理 PET画像の再構成, スパース信号の復元, 画像の超解像, など
航空宇宙 衛星の軌道設計, ロケットの打ち上げ最適化, 航空機の飛行経路最適化, など
ロボティクス ロボットの動作計画, ロボットアームの軌道最適化, 脚ロボットの歩行パターン生成, など
バイオインフォマティクス タンパク質の立体構造予測, 遺伝子ネットワークの推定, 薬物の分子設計, など
材料科学 材料の組成最適化, 結晶成長プロセスの最適化, 3Dプリンティングでの形状最適化, など
環境科学 大気汚染物質の拡散モデリング, 生態系モデリング, 気候変動対策の最適化, など
スポーツ分析 選手の戦略最適化, チームの編成最適化, トレーニング計画の最適化, など
ゲーム理論 ナッシュ均衡の計算, メカニズムデザイン, 複雑なゲームの戦略最適化, など

 

このように、非線形性を含む最適化問題は実社会のさまざまな意思決定に現れており、非線形計画法はそれらを解決するための強力なツールとなっています。

ただ、知らないがために、多くの人がこの恩恵に預かれず、感覚で「えぃ！」と物事を決めているような気がします。

この機会にマスターしましょう！ そこまで大げさなものではありません。ただし、深みにはまるとどこまでのはまれるので、ほどほどにしましょう。

非線形計画問題とは？

　最適化問題の種類

最適化問題は、目的関数を最小化（または最大化）する変数の値を見つける問題です。

最適化問題は、制約条件の有無や目的関数・制約条件の性質によって、いくつかの種類に分類されます。

  • 線形計画問題（LP）：目的関数と制約条件がすべて線形
  • 非線形計画問題（NLP）：目的関数または制約条件が非線形
  • 混合整数計画問題（MIP）：変数の一部が整数値をとる

 

線形計画問題は、シンプレックス法などの効率的なアルゴリズムで解くことができます。

一方、非線形計画問題は、一般に解くことが難しく、大域的最適解を見つけることが保証されていません。

 

例えば、以下の右のRastrigin関数は非線形性が強く、多数の局所最適解を持つことが知られています。

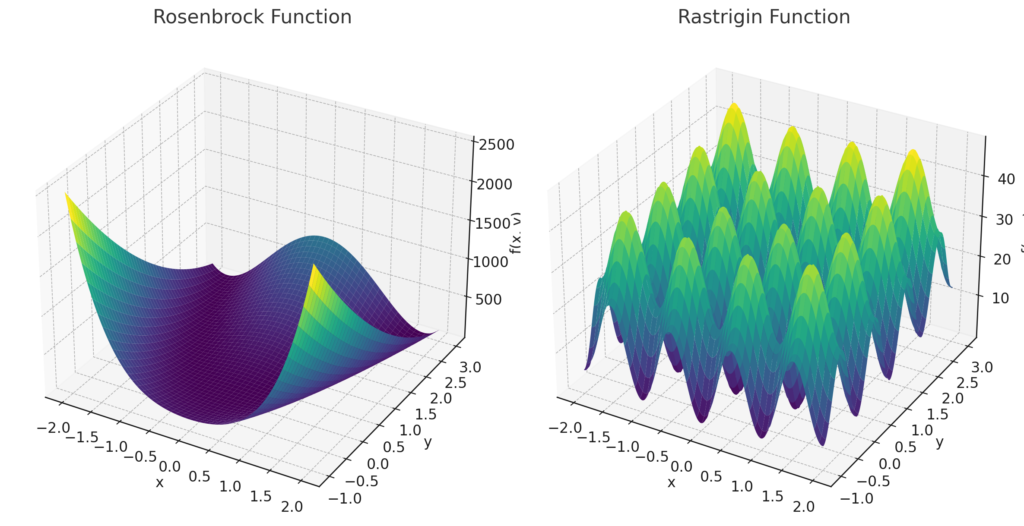
上の左のRosenbrock関数は、局所的最適解が1つありそれが大域的最適解ですが、Rosenbrockの谷の影響で最適解にたどり着けず、アルゴリズムの探索停止点が最適解として表示されます。非線形最適化問題で広く使用される、アルゴリズムの性能テストで利用される関数の一つです。

 

　非線形計画問題の定式化

非線形計画問題を定式化すると、以下のようになります。

\displaystyle \begin{matrix} \displaystyle \min_{x \in \mathbb{R}^n} \quad & f(x) \\ \text{subject to} \quad & g_i(x) \leq 0, \quad i = 1, \ldots, m \\ & h_j(x) = 0, \quad j = 1, \ldots, p \end{matrix}

ここで、f(x)は目的関数、g_i(x)は不等式制約、h_j(x)は等式制約を表します。

非線形計画問題は、現実世界の複雑な問題をモデル化するのに適していますが、その解法は容易ではありません。

 

　局所最適解と大域的最適解

非線形計画問題を解く際に、局所最適解と大域的最適解の概念を理解することが重要です。

ある解 \hat{x} が局所最適解であるとは、\hat{x} の十分小さな近傍内 \mathcal{B}(\hat{x}, \epsilon) で、\hat{x} が最適解となることを指します。

\displaystyle \exists \epsilon > 0 \, s.t. \, f(\hat{x}) \leq f(x), \forall x \in \mathcal{B}(\hat{x}, \epsilon)

ある解 \hat{x} が大域的最適解であるとは、実行可能領域全体 \mathcal{D} で、\hat{x} が最適解となることを指します。

\displaystyle f(x^*) \leq f(x), \forall x \in \mathcal{D}

局所最適解は、近傍内では最適ですが、実行可能領域全体で最適であるとは限りません。一方、大域的最適解は、実行可能領域全体で最適です。

非線形計画問題では、複数の局所最適解が存在する可能性があり、それらの中から大域的最適解を見つけることが目標となります。なぜならば、局所最適解の中に大域的最適解があるからです。

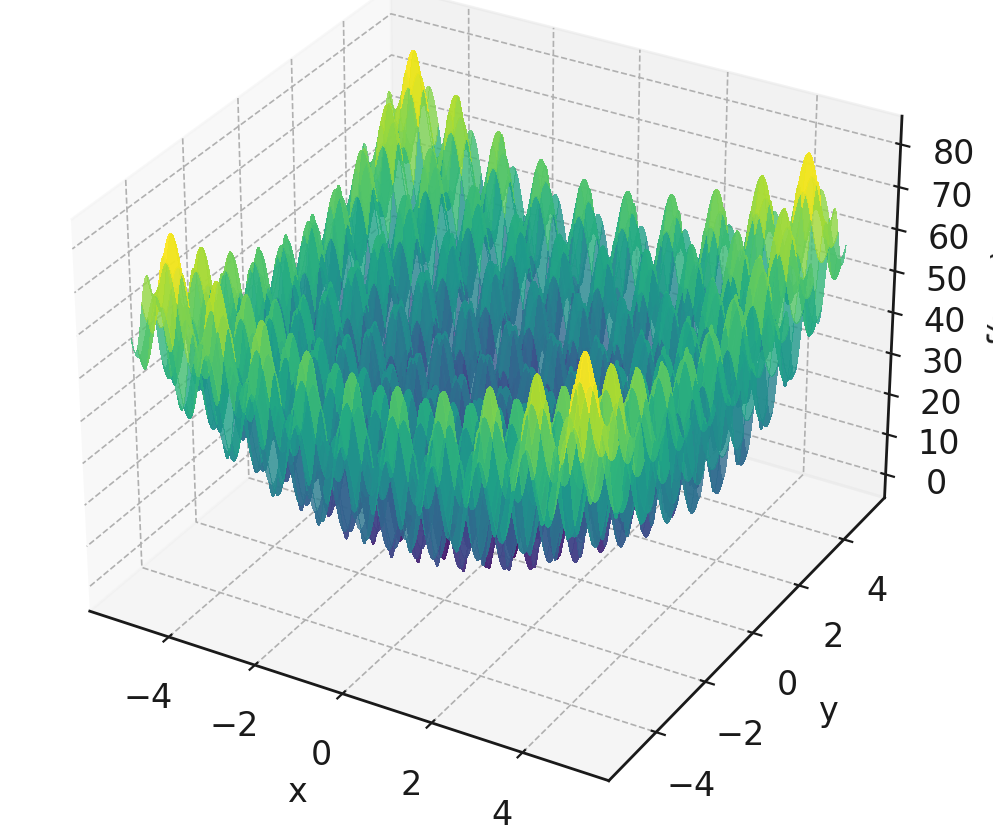
例えば、先ほどのレーストリガン関数 f(x, y) = 20 + x^2 + y^2 - 10(\cos(2\pi x) + \cos(2\pi y)は、多数の局所最適解を持ちます。その中に大域的最適解があり f(0, 0) = 0 です。

勾配ベースの最適化手法を使うと最適解を見つけることができます。しかし、初期点に応じて異なる局所最適解に収束します。運よく f(0, 0) = 0 に収束すれば大域的最適解が見つかります。

ここである問題が起きます。f(0, 0) = 0 が単なる局所的最適解なのか、それとも大域的最適解なのか、というも問題です。他のすべての局所的最適解と比べなければ分かりません。問題によっては、すべての局所的最適解を見つけ出し列挙するのが困難な場合もあります。

 

　凸最適化問題と非凸最適化問題

最適化問題は、線形なのか非線形なのか、という分類の仕方以外に、凸最適化なのか非凸最適化なのか、という分類の仕方もあります。

ここでは、凸関数や凸集合の定義や説明は省きます。気になる方は、最適化理論の教科書などを一読ください。難しいものではございません。

凸最適化問題は、目的関数が凸関数、実行可能領域が凸集合であり、任意の局所最適解が大域的最適解となります。

線形計画問題は凸最適化問題です。非線形計画問題はどうかというと、凸計画最適化問題の非線形計画問題もあります。その場合、非常にラッキーです。「局所最適解＝大域的最適解」だからです。

一方、非凸最適化問題は、複数の局所最適解が存在する可能性があり、大域的最適解を見つけることが困難です。

非線形計画問題の多くは非凸最適化問題であり、大域的最適解を求めることは容易ではありません。

要するに、多くの非線形計画問題の目的関数は非凸関数、もしくは、実行可能領域（制約条件により定義された領域）が非凸集合だということです。

 

大域的最適化の難しさ

非線形計画問題の大域的最適化は、非線形性、非凸性、多峰性、次元の呪いなどの理由から、本質的に難しい問題となっています。

ちなみに、さらに整数性が組み込まれる（例：非線形な混合整数計画問題）とさらに難しくなります。

 

　非線形性と非凸性

非線形関数は、複雑な形状を持ち、複数の極値（局所最適解）を持つ可能性があります。

また、非凸関数では、大域的最適解の存在や一意性が保証されていません。

これらの性質が、大域的最適化を困難にしています。

 

　多峰性と局所解の存在

多峰性（multimodality）は、関数が複数の極値を持つ性質を指します。

非線形関数は多峰性を示すことが多く、これにより複数の局所最適解が存在します。

局所最適解は、大域的最適解ではないにもかかわらず、局所的には最適であるため、最適化アルゴリズムが局所最適解に収束してしまう可能性があります。

 

　次元の呪い

最適化問題の変数の数（次元）が増加すると、探索すべき空間が指数的に増大します。

これを「次元の呪い」と呼びます。

次元の呪いにより、大域的最適解を見つけるために必要な計算量が爆発的に増加し、現実的な時間で解を得ることが困難になります。

 

　計算量の爆発

大域的最適解を保証するためには、原理的には実行可能領域全体を探索する必要があります。

しかし、実行可能領域が広く、次元が高い場合、全探索は現実的ではありません。

また、非線形性や非凸性により、効率的な探索が困難になります。

 

　大域的最適性の保証の難しさ

非線形計画問題では、大域的最適性を保証することが難しいという本質的な問題があります。

ある解が大域的最適解であることを証明するためには、実行可能領域全体を調べる必要がありますが、それは一般に不可能です。

そのため、多くの大域的最適化手法は、確率的に大域的最適解を見つけることを目指しますが、完全な保証を与えることはできません。

つまり、非常に簡単な問題でない限り、大域的最適化を見つけること、もしくは、その局所的最適解が大域的最適解であることを保証することも、できません。

そこで、妥協解という概念が登場します。人間に見つけられる最適解は、今のコンピュータサイエンスの技術では妥協解どまりです。現在の玩具のような量子コンピュータではなく、本格的な量子コンピュータが実現されれば可能かもしれません。

 

Pythonで制約付き非線形計画問題を解く（SciPy版）

ここでは、Pythonでよく使われる科学計算ライブラリであるScipyを使って非線形計画問題を定式化する方法について簡単に説明します。

 

　取り扱う非線形計画問題

今回は、以下の非線形計画問題を扱います。

\displaystyle \begin{array}{ll} \displaystyle \min_{x \in \mathbb{R}^2} \quad & f(x_0,x_1) = (1 - x_0)^2 + 100 (x_1 - x_0^2)^2 \\ \text{subject to} \quad & x_0-2x_1 - 2 \leq 0 \\ & e^{x_1}- 8 \leq 0 \\ & x_0^2 + x_1^2 - 10 \leq 0 \\ & -5 \leq x_0 \leq 5 \\ & -5 \leq x_1 \leq 5 \end{array}

 

目的関数はRosenbrock関数と呼ばれる、大域的最適解を求めるのが非常に難しい問題です。ちなみに解は、(x_0,x_1)=(1,1)です。おそらく、SciPyでは上手くいきません。

 

　目的関数の定義

目的関数は、最適化したい関数です。Pythonでは、目的関数を関数オブジェクトとして定義します。

Pythonの関数はオブジェクトとして扱うことができます。これにより、関数を変数に代入したり、他の関数の引数として渡したりできます。

NumPyは、多次元配列を効率的に処理するためのPythonライブラリです。目的関数の計算をベクトル化することで、計算速度を向上させることができます。

以下、コードです。

def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

 

　制約条件の定義

制約条件は、変数が満たすべき条件です。制約条件には、等式制約と不等式制約があります。

制約条件で利用する関数を定義した後に、制約条件を定義します。

以下、コードです。

# 制約条件の定義
def constraint1(x):
    return x[0] - 2 * x[1] - 2

def constraint2(x):
    return np.exp(x[1]) - 8

def constraint3(x):
    return x[0]**2 + x[1]**2 - 10

cons = ({'type': 'ineq', 'fun': constraint1},
        {'type': 'ineq', 'fun': constraint2},
        {'type': 'ineq', 'fun': constraint3})

 

この例では、3つの不等式制約の関数を定義し、consリストにまとめています。

  • 等式制約：constraint関数の戻り値が0になるように定義します。consリストの type は eq です。
  • 不等式制約：constraint関数の戻り値が0以下になるように定義します。consリストの type は ineq です。

 

関数を定義せず、制約条件を定義することもできます。

以下、コードです。

# 制約条件の定義
cons = ({'type': 'ineq', 'fun': lambda x: x[0] - 2 * x[1] + 2},
        {'type': 'ineq', 'fun': lambda x: np.exp(x[1]) - 8},
        {'type': 'ineq', 'fun': lambda x: x[0]**2 + x[1]**2 - 10})

 

どちらも同じ制約条件です。

 

　ペナルティ関数によるソフト制約の導入

ハードな制約条件の代わりに、制約条件の違反に対してペナルティを課すことで、ソフトな制約条件を導入できます。

ペナルティ関数を目的関数に加えることで、制約条件を満たさない解を避けるようにできます。

最初に、ペナルティ関数を定義し、それを目的関数に追加し定義します。

以下は、変数が-2から2の範囲を超えた場合にペナルティを課すコード例です。

def penalty(x):
    penalty = max(abs(x[0]) - 2, 0) + max(abs(x[1]) - 2, 0)
    return penalty

def objective_with_penalty(x):
    return objective(x) + 1e+10 * penalty(x)

 

1e+10 は 1 の 10乗 を意味し、10,000,000,000 に相当する。

 

　変数の上下限制約

変数の取り得る値の範囲を指定します。bounds で、各変数の下限と上限を指定します。

以下は、下限を-5、上限を5に設定した場合のコード例です。

bounds = ((-5, 5), (-5, 5))

 

　変数変換

スケーリングや正規化などの変数変換を実施したい場合があります。そのときは、変数変換用の関数を定義し、それを利用します。

変数変換用の関数は、データから学習したもの（例：機械学習モデルや主成分モデルなど）でも構いません。多くの場合、そのまま利用できます。

以下は、スケーリング用の関数を定義した後に、目的変数に利用した場合のコード例です。

def scale(x):
    return [2 * (x[0] + 5) / 10, 2 * (x[1] + 5) / 10]

def objective_scaled(x):
    x_scaled = scale(x)
    return objective(x_scaled)

 

　コードの全体像

変数変換やソフト制約を付けていない場合の、コード全体です。

from scipy.optimize import minimize
import numpy as np

# 目的関数の定義
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約条件の定義
def constraint1(x):
    return x[0] - 2 * x[1] - 2

def constraint2(x):
    return np.exp(x[1]) - 8

def constraint3(x):
    return x[0]**2 + x[1]**2 - 10

cons = ({'type': 'ineq', 'fun': constraint1},
        {'type': 'ineq', 'fun': constraint2},
        {'type': 'ineq', 'fun': constraint3})
        
# 最適化する変数の下限と上限
bounds = ((-5, 5), (-5, 5))

# 初期値
x0 = [0, 0]

# 最適化
res = minimize(
    objective, 
    x0, 
    method='SLSQP', 
    constraints=cons, 
    bounds=bounds)

# 最適解
print(res.x)

 

以下、実行結果です。

[<span>1.99999999e+00 -6.09215107e-16</span>]

 

最適解は(x_0,x_1)=(1,1)ですが、異なるようです。SciPyの限界です。初期値を上手く選ぶと到達できます。

 

ソフト制約のみを付けた場合の、コード全体です。

from scipy.optimize import minimize
import numpy as np

# 目的関数の定義
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# ペナルティ関数付き目的関数の定義
def penalty(x):
    penalty = max(abs(x[0]) - 2, 0) + max(abs(x[1]) - 2, 0)
    return penalty

def objective_with_penalty(x):
    return objective(x) + 1e+10 * penalty(x)

# 制約条件の定義
def constraint1(x):
    return x[0] - 2 * x[1] - 2

def constraint2(x):
    return np.exp(x[1]) - 8

def constraint3(x):
    return x[0]**2 + x[1]**2 - 10

cons = ({'type': 'ineq', 'fun': constraint1},
        {'type': 'ineq', 'fun': constraint2},
        {'type': 'ineq', 'fun': constraint3})
        
# 最適化する変数の下限と上限
bounds = ((-5, 5), (-5, 5))

# 初期値
x0 = [0, 0]

# 最適化
res = minimize(
    objective_with_penalty, 
    x0, 
    method='SLSQP', 
    constraints=cons, 
    bounds=bounds)

# 最適解
print(res.x)

 

以下、実行結果です。

[<span>1.99999999e+00 -6.09215107e-16</span>]

 

変数変換を組み込んだ場合の、コード全体です。

from scipy.optimize import minimize
import numpy as np

# 目的関数の定義
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 変数変換用の関数の定義
def scale(x):
    return [2 * (x[0] + 5) / 10, 2 * (x[1] + 5) / 10]

# 目的関数の再定義
def objective_scaled(x):
    x_scaled = scale(x)
    return objective(x_scaled)

def objective_with_penalty(x):
    return objective(x) + 1e+10 * penalty(x)

# 制約条件の定義
def constraint1(x):
    return x[0] - 2 * x[1] + 2

def constraint2(x):
    return np.exp(x[1]) - 8

def constraint3(x):
    return x[0]**2 + x[1]**2 - 10

cons = ({'type': 'ineq', 'fun': constraint1},
        {'type': 'ineq', 'fun': constraint2},
        {'type': 'ineq', 'fun': constraint3})
        
# 最適化する変数の下限と上限
bounds = ((-5, 5), (-5, 5))

# 初期値
x0 = [0, 0]

# 最適化
res = minimize(
    objective_scaled, 
    x0, 
    method='SLSQP', 
    constraints=cons, 
    bounds=bounds)

# 最適解
print(res.x)

 

以下、実行結果です。

[<span>0. 0.</span>]

 

　多峰性関数であるAckley関数を目的関数にした例

多数の局所最適解を持つことが知られている以下のAckley関数を目的関数にし最小化する例を示します。最適解は (x_0,x_1)=(-3,4) で、最適値は 0 です。

 

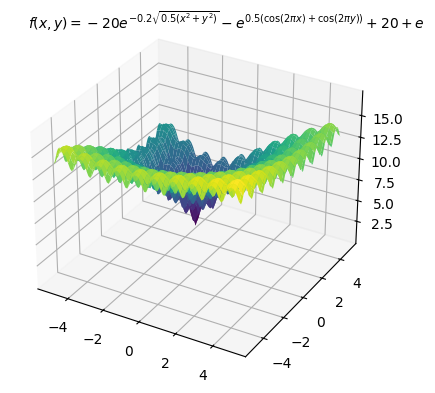
以下、コードです。変数の上下限制約のみ入れています。

from scipy.optimize import minimize
import numpy as np

# 目的関数の定義
def objective(x):
    a = 20
    b = 0.2
    c = 2 * np.pi
    n = len(x)
    x_offset = np.array([x[0] + 3, x[1] - 4])
    sum_sq_term = -a * np.exp(-b * np.sqrt(sum(x_offset**2) / n))
    cos_term = -np.exp(sum(np.cos(c * x_offset) / n))
    return sum_sq_term + cos_term + a + np.e
        
# 最適化する変数の下限と上限
bounds = ((-5, 5), (-5, 5))

# 初期値
x0 = [0, 0]

# 最適化
res = minimize(
    objective, 
    x0, 
    method='SLSQP', 
    bounds=bounds)

# 最適解
print(res.x)
print(res.fun)

 

以下、実行結果です。

[-2.99995187  3.04773342]
2.5799278583650787

 

最適解は(x_0,x_1)=(-3,4)ですが、到達できませんでした。SciPyの限界です。初期値を上手く選ぶと到達できます。

 

SciPyによる最適化は手軽だが限界もある

SciPyは、Pythonの科学計算ライブラリの中で最も広く使われているものの1つで、最適化問題を解くための様々な手法を提供しています。

SciPyを使った最適化は、比較的簡単に実装できるため、多くの場合に適しています。

 

　SciPyによる最適化の特徴

SciPyの最適化モジュール（scipy.optimize）は、以下のようなメリットを持っています。

  • 豊富な最適化アルゴリズム
    • 局所最適化手法（BFGS, L-BFGS-B, SLSQP, Nelder-Meadなど）
    • 大域的最適化手法（Basin-hopping, Differential Evolutionなど）
    • 最小二乗問題用の手法（least_squares）
  • 簡潔で直感的なインターフェース
    • 目的関数や制約条件をPythonの関数で定義
    • 最適化の設定をキーワード引数で指定
  • NumPyとの親和性
    • NumPyの配列を直接扱える
    • 目的関数や制約条件の計算をベクトル化できる
アルゴリズム 分類 特徴 適用問題
BFGS 局所最適化
  •  準ニュートン法の一種
  • 関数の勾配情報を利用
  • 二次収束性がある
  • 制約条件のない最適化問題
  • 範囲制約（変数の上限下限）には対応
  • 大規模な問題
L-BFGS-B 局所最適化
  • BFGSの低メモリ版
  • 変数の範囲制約に対応
  • 関数の勾配情報を利用
  • 制約条件のない最適化問題
  • 範囲制約（変数の上限下限）には対応
  • 大規模な問題
SLSQP 局所最適化
  • 逐次二次計画法
  • 非線形の等式・不等式制約に対応
  • 関数の勾配情報を利用
  • 制約条件のある最適化問題
  • 中小規模の問題
Nelder-Mead 局所最適化
  • シンプレックス法の一種
  • 関数の勾配情報不要
  • 収束性が遅い
  • 制約条件のない最適化問題
  • 低次元の問題
Basin-hopping 大域的最適化
  • マルチスタート法の一種
  • 局所最適化とランダムな摂動を組み合わせ
  • 関数の勾配情報不要
  • 複数の局所的最適解がある問題
  • 低次元の問題
Differential Evolution 大域的最適化
  • 進化的アルゴリズムの一種
  • 集団ベースの探索
  • 関数の勾配情報不要
  • 複数の局所的最適解がある問題
  • 中高次元の問題
least_squares 最小二乗問題
  • 非線形最小二乗問題に特化
  • ヤコビアン行列の情報を利用可能
  • 信頼領域反射法や犬足法など複数のアルゴリズムを選択可能
  • 非線形最小二乗問題
  • 中小規模の問題

 

ただし、SciPyの最適化モジュールには以下のようなデメリットもあります。

  • 大規模な問題には不向き
    • 変数の数が多い場合、収束が遅くなる
    • スパース行列を利用した大規模最適化には対応していない
  • 高度なカスタマイズが難しい
    • アルゴリズムの詳細設定を変更するのが難しい
    • 特殊な問題構造を利用した最適化手法を実装するのが難しい

 

問題の規模が大きい場合や、高度な設定が必要な場合は、他の最適化ライブラリを検討する必要があります。

しかし、多くの中小規模の問題では、SciPyが最も簡単で効果的な選択肢と言えます。

 

（参考）Python SciPyで手を動かしながら学ぶ数理最適化

SciPyの最適化問題の解き方については、以下の一連の記事（Python SciPyで手を動かしながら学ぶ数理最適化）で、ちょっとだけ詳しく説明していますので、興味ある方は参考にしてください。

 

Pythonの最適化ライブラリの紹介

Pythonには、非線形最適化問題を解くための様々なライブラリが存在します。ここでは、代表的なライブラリを紹介します。

 

　SciPy.optimize

先ずは、先ほど紹介したSciPyです。

SciPyは、科学技術計算のためのPythonライブラリです。SciPyのoptimizeモジュールには、様々な最適化アルゴリズムが実装されています。

BFGS法やL-BFGS-B法は、準ニュートン法の一種で、目的関数の勾配情報を利用して最適解を探索します。SLSQP法は、逐次二次計画法の一種で、制約条件付き最適化問題に適しています。

Basinhopping法は、マルチスタート局所探索法の一種で、ランダムに初期点を生成し、局所探索を繰り返すことで大域的最適解を探索します。Differential Evolution法は、進化計算の一種で、集団を進化させることで大域的最適解を探索します。

 

　CyIPOPT

CyIPOPTは、非線形最適化ソルバーIPOPTのPythonインターフェースです。IPOPTは、内点法を用いた大規模な非線形最適化問題に適したソルバーです。

CyIPOPTは、IPOPTソルバーのC++コードをPythonから直接呼び出し使用します。これにより、IPOPTの機能を簡単にPythonから利用できるのが特徴です。

そのため、CyIPOPTを使うことで、大規模な問題をPythonで扱うことができます。

 

　PyGMO

PyGMOは、大域的最適化のためのオープンソースライブラリで、様々な大域的最適化アルゴリズムが実装されています。

PyGMOには、遺伝的アルゴリズム、差分進化、粒子群最適化、暗黒物質探索など、様々な大域的最適化アルゴリズムが実装されています。

 

　その他の最適化問題に利用できるPythonライブラリ

  • Pyomo: 最適化モデリング言語のPythonインターフェース
  • DEAP: 進化計算のためのPythonライブラリ
  • Platypus: 多目的最適化のためのPythonライブラリ
  • OpenOpt: 非線形最適化のためのPythonフレームワーク
  • GPflowOpt: ベイズ最適化のためのPythonライブラリ

これらのライブラリは、それぞれ異なる特徴を持っています。問題の性質や要件に応じて、適切なライブラリを選択することが重要です。

 

まとめ

今回は、非線形計画問題と大域的最適化の基礎について説明しました。

まず、非線形計画問題とは何か、局所最適解と大域的最適解の違い、大域的最適化の難しさについて説明しました。次に、Pythonを使って非線形計画問題を定式化し解く方法を紹介しました。一番簡単なSciPyを使った方法です。

最後に、Pythonの代表的な最適化ライブラリについて紹介しました。SciPy.optimize、CyIPOPT、PyGMOなどのライブラリの特徴と使い方について解説しました。取り急ぎ、実務的にはこの3つのライブラリで十分です。

非線形計画問題は、現実世界の様々な問題を数理的にモデル化するのに適しています。しかし、その解法は一般に困難で、大域的最適解を求めることは容易ではありません。Pythonの最適化ライブラリを使うことで、非線形計画問題に対して効率的に解を求めることができます。

次回以降、Pythonを使った大域的最適化手法の実装と応用について、解説していきます。

次回は、メタヒューリスティクスによる大域的最適化手法を実践するお話しをいたします。

【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！– 【第2回】Pythonによる大域的最適化手法の実装（メタヒューリスティクス編） –