前回は、非線形計画問題の基礎と、Pythonを使った定式化の方法について学びました。

非線形計画問題は、現実世界の様々な問題を数理的にモデル化するのに適していますが、その解法は一般に困難で、大域的最適解を求めることは容易ではありません。

【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！– 【第1回】非線形計画問題と大域的最適化の基礎 –

そこで、今回は、非線形計画問題の大域的最適解に挑戦するための手法として、メタヒューリスティクスに着目します。

メタヒューリスティクスは、問題依存性が低く、大域的最適解の探索に適した最適化手法の総称です。代表的なメタヒューリスティクスとして、遺伝的アルゴリズム（GA）や粒子群最適化（PSO）などがあります。

まずメタヒューリスティクスの概要と特徴について説明します。次に、GAとPSOの基本的な流れとPythonでの実装例を紹介します。

さらに、大域的最適化ライブラリであるPyGMOを用いて、GAとPSOを非線形計画問題に適用する方法を解説します。最後に、メタヒューリスティクスの長所と短所、チューニングのコツについても議論します。

メタヒューリスティクスは、非線形計画問題の大域的最適化に有効なアプローチですが、その性能はアルゴリズムのパラメータ設定に大きく依存します。

メタヒューリスティクスとは？

メタヒューリスティクスは、問題固有の知識を利用せずに、探索空間を効率的に探索するための、最適化問題を解くための汎用的な手法の総称です。

局所的な探索と大域的な探索のバランスを取ることで、大域的最適解の発見を目指します。

 

　メタヒューリスティクスの特徴

問題依存性が低い
メタヒューリスティクスは、問題の特性に依存しない一般的な探索戦略を提供します。そのため、様々な問題に適用可能です。

大域的最適解の探索に適している
メタヒューリスティクスは、局所的な探索と大域的な探索のバランスを取ることで、大域的最適解の発見を目指します。これは、非線形計画問題のような複雑な問題に対して特に有効です。

局所解からの脱出メカニズムを持つ
メタヒューリスティクスは、局所解に陥った場合でも、そこから脱出するためのメカニズムを持っています。これにより、探索が局所解に停滞することを防ぎます。

 

　代表的なメタヒューリスティクス

遺伝的アルゴリズム（GA）
生物の進化過程を模倣した探索手法。選択、交叉、突然変異の操作を繰り返すことで、良好な解を探索します。

粒子群最適化（PSO）
鳥や魚の群れの行動を模倣した探索手法。粒子が個々の最良解と全体の最良解の情報を共有しながら、探索空間を移動します。

シミュレーテッドアニーリング（SA）
金属の焼きなまし過程を模倣した探索手法。温度パラメータを徐々に下げながら、確率的に解を更新します。

タブーサーチ（TS）
局所解からの脱出を目的とした探索手法。直前の探索で訪れた解への移動を禁止（タブー）することで、サイクルに陥ることを防ぎます。

アントコロニー最適化（ACO）
アリの集団行動を模倣した探索手法。フェロモンの濃度に基づいて確率的に解を構築します。

これらのメタヒューリスティクスは、それぞれ独自の探索戦略を持っていますが、いずれも大域的最適解の発見を目指すという共通の目的を持っています。

 

PyGMOライブラリ

PyGMOは、大域的最適化ライブラリです。PyGMOには、様々なメタヒューリスティクスが実装されており、並列化にも対応しています。

　PyGMOの概要

PyGMOの主な特徴は以下の通りです。

• 大域的最適化ライブラリ：PyGMOは、大域的最適化問題を解くために設計されたライブラリです。
• 様々なアルゴリズムを提供：PyGMOには、GA、PSO、Differential Evolution (DE)、Ant Colony Optimization (ACO)など、多数のメタヒューリスティクスが実装されています。
• 並列化にも対応：PyGMOは、島モデルと呼ばれる並列化手法を用いることで、効率的に最適化を行うことができます。

 

　PyGMOのインストール

PyGMOは、pip（Pythonのパッケージ管理システム）を使ってインストールできます。

以下のコマンドを実行してください。

pip install pygmo

 

Anacondaなどのconda環境を使っている場合は、以下のコマンドでインストールすることもできます。

conda install -c conda-forge pygmo

 

　利用可能な主な最適化アルゴリズム

PyGMOで利用可能な主な最適化アルゴリズムの一覧表です。

アルゴリズム名	分類	特徴	メリット	デメリット
(μ+λ)-ES	進化戦略	複数の親個体から子個体を生成し、親個体と子個体の中から選択	探索効率が高い	パラメータ設定が複雑
CMA-ES	進化戦略	共分散行列適応戦略を使用	高次元の問題に対応可能	パラメータ設定が複雑
Simple Genetic Algorithm (SGA)	遺伝的アルゴリズム	基本的な遺伝的アルゴリズム	シンプルで実装が容易	探索効率が低い
Particle Swarm Optimization (PSO)	群知能	粒子の集団が協調して最適解を探索	実装が容易で収束が速い	局所解に陥りやすい
Differential Evolution (DE)	差分進化	個体間の差分を利用して新しい個体を生成	連続最適化問題に適している	局所解に陥りやすい
Simulated Annealing (SA)	確率的アルゴリズム	金属の焼きなましを模倣して最適解を探索	大域的最適解の探索に適している	収束速度が遅い
NSGA-II	その他	多目的最適化アルゴリズム	パレート最適解の探索に適している	計算コストが高い
MOEA/D	その他	多目的最適化アルゴリズム	パレート最適解の探索に適している	パラメータ設定が複雑

 

他にもたくさん実装されています。

各アルゴリズムには、それぞれ特徴やメリット・デメリットがあるため、問題の性質に応じて適切なアルゴリズムを選択することが重要です。

アルゴリズムのパラメータ設定も、最適化の性能に大きな影響を与えるため、適切なパラメータを見つけることも重要です。

 

PyGMOを使用した一般的なプロセス

PyGMOを使用した大域的最適化の一般的なプロセスを、具体的な例を用いて説明します。

 

　ステップ1: 問題の定義

最初に、最適化したい問題を定義します。

ここでは、単純な2次関数の最小化を例として使用します。この関数は任意の次元で定義され、目的は変数の二乗の合計を最小化することです。

import pygmo as pg
import numpy as np

class CustomProblem:
    # 初期化
    def __init__(self, dim):
        self.dim = dim
    # 目的関数
    def fitness(self, x):
        return [sum(np.array(x)**2)]
    # 各変数（次元）の範囲
    def get_bounds(self):
        return ([-5] * self.dim, [5] * self.dim)
    # 目的変数の数
    def get_nobj(self):
        return 1
    # 問題名
    def get_name(self):
        return "Custom Quadratic Problem"

 

PyGMOではCustomProblemクラスを使って、ユーザー独自の最適化問題を定義します。

CustomProblemクラスを定義することで、ユーザーは最適化したい独自の目的関数、制約条件、変数の範囲などを指定することができます。

これにより、PyGMOの最適化アルゴリズムを使用して、その問題を効率的に解くことが可能になります。

 

CustomProblemクラスを定義する際には、以下のメソッドを実装する必要があります。

• fitness(self, x): このメソッドは、解候補xに対する目的関数の値（または複数の目的関数の値のリスト）を計算し、返します。
• get_bounds(self): このメソッドは、最適化する各変数の下限と上限を定義し、それらの値のタプルを返します。

必要に応じて、以下のメソッドも実装することができます：

• get_nobj(self): 問題が持つ目的関数の数を返します（デフォルトは1）。
• get_nic(self): 問題が持つ不等式制約の数を返します（デフォルトは0）。
• get_nec(self): 問題が持つ等式制約の数を返します（デフォルトは0）。

これらのメソッドを通じて、PyGMOは与えられた最適化問題の構造を理解し、適切なアルゴリズムを用いて解を求めることができます。

 

　ステップ2: アルゴリズムの選択

次に、問題を解くためのアルゴリズムを選択します。

PyGMOには多くの大域的最適化アルゴリズムが実装されており、ここでは差分進化（DE）を使用します。差分進化は、特に連続変数の最適化問題に対して効果的なアルゴリズムです。

algo = pg.algorithm(pg.de(gen=1000))

 

pg.algorithm()は、PyGMOでアルゴリズムを作成するためのコンストラクタ関数です。

この関数により、指定されたアルゴリズムに基づいて最適化プロセスを実行するオブジェクトが生成されます。

• pg.algorithm()の引数としてアルゴリズムを指定します。この例では差分進化アルゴリズムpg.de()を指定しています。
• pg.de()の引数として世代数gen=1000を指定しています。アルゴリズムが1000世代にわたって進化させることを意味しています。

この例ではalgoが、そのオブジェクトです。その後のステップで、特定の最適化問題（pg.problemオブジェクト）に適用され、最適解の探索を行います。

 

ちなみに、他のアルゴリズムを指定するときには、pg.algorithm()の引数の指定を変えるだけです。

以下一例です。

# 粒子群最適化（Particle Swarm Optimization, PSO）
algo = pg.algorithm(pg.pso(gen=1000))

# 遺伝的アルゴリズム（Genetic Algorithm, GA）
algo = pg.algorithm(pg.sga(gen=1000))

# シミュレーテッドアニーリング（Simulated Annealing, SA）
algo = pg.algorithm(pg.simulated_annealing())

# 共分散行列適応進化戦略（Covariance Matrix Adaptation Evolution Strategy, CMA-ES）
algo = pg.algorithm(pg.cmaes(gen=1000))

 

　ステップ3: 初期個体群の生成と進化

問題とアルゴリズムを設定したら、初期個体群を生成し、進化させることで問題の解を探索します。

個体群のサイズや進化の世代数は、問題の難易度や次元数に応じて調整することができます。

# 問題の次元を設定
dim = 5
prob = pg.problem(CustomProblem(dim))

# 初期個体群を生成
pop = pg.population(prob, 100)

# 個体群を進化させる
pop = algo.evolve(pop)

 

最初に言葉の定義です。

問題の次元とは、最適化を行う際に調整可能な変数（もしくはパラメータ）の数を指します。

状況の応じて最適化対象が変わるため（例：特徴量、モデルパラメータ、ハイーパラメータなど）、次元という表現がなされます。

例えば、線形回帰モデルを最小二乗法でモデルパラメータを学習するとき、最適化対象はモデルパラメータです。例えば、学習済みの機械学習モデルを使い、最適な特徴量（説明変数）の値を求めるとき、最適化対象は特徴量（説明変数）になります。

 

次に、コードの説明を簡単にします。

pg.problem(CustomProblem(dim))は、CustomProblemクラスのインスタンスを作成し、それをPyGMOの問題として設定しています。このインスタンスprobは、5次元（dim = 5）の特定の最適化問題を表しています。

pg.population(prob, 100)は、定義した問題probに対して、100個の解候補（個体）からなる初期個体群を生成します。個体群の各個体は、問題の潜在的な解を表し、最適化プロセスを通じて改善されます。

algo.evolve(pop)は、事前に選択された最適化アルゴリズム（このコードではalgoに割り当てられています）を使用して、初期個体群popを進化させ、より良い解へと進化していきます。

 

　ステップ4: 結果の表示

最適化プロセスの後、最良の解（champion_x）とその適応度（champion_f）を表示します。

print(f"Best solution: {pop.champion_x}")
print(f"Best fitness: {pop.champion_f}")

 

このプロセスでは、PyGMOを使用して、カスタムの問題に対する大域的最適化を行います。

PyGMOに実装されている多様なアルゴリズムを利用することで、様々な種類の最適化問題に対して効果的な解法を見つけることができます。問題の性質や要求される精度に応じて、適切なアルゴリズムとパラメータを選択することが重要です。

 

次から、比較的メジャーな遺伝的アルゴリズム（GA）と粒子群最適化(PSO)について、PyGMOの使い方とともに説明します。

その後、前回取り扱ったRosenbrock関数を最小化する制約付き非線形計画問題の解き方を簡単に説明します。

 

遺伝的アルゴリズム(GA)の概要とPython実装

遺伝的アルゴリズム（GA）は、生物の進化過程を模倣した代表的なメタヒューリスティクスです。GAは、選択、交叉、突然変異の操作を繰り返すことで、良好な解を探索します。

 

　GAの基本的な流れ

GAの基本的な流れは以下の通りです。

1. 初期集団の生成：探索空間上にランダムに個体を配置し、初期集団を生成します。
2. 適応度の評価：各個体の適応度を評価します。適応度は、問題の目的関数に基づいて計算されます。
3. 選択：適応度の高い個体を優先的に選択します。選択された個体は、次世代に受け継がれます。
4. 交叉：選択された個体の一部をペアにして、遺伝子を交換します。これにより、新しい個体が生成されます。
5. 突然変異：一定の確率で、個体の遺伝子を変異させます。これにより、探索の多様性が維持されます。

これらの操作を繰り返すことで、集団全体の適応度が徐々に向上し、最終的に良好な解が得られます。

 

　GAの特徴

GAには以下のような特徴があります。

生物の進化過程を模倣
GAは、生物の進化過程における自然選択と遺伝的な変化を模倣しています。

集団ベースの探索
GAは、複数の個体からなる集団を用いて探索を行います。これにより、探索空間を効率的に探索できます。

確率的な遷移ルール
GAでは、選択、交叉、突然変異といった操作が確率的に行われます。これにより、通常の決定的探索（Deterministic Search）では見落とされがちな解も発見できます。

 

ちなみに、決定的探索（Deterministic Search）とは、アルゴリズムの実行結果が初期状態とアルゴリズム自体にのみ依存し、ランダム性がない探索方法を指します。多くの最適化アルゴリズムは決定的探索です。

これは、ランダムな要素を含む確率的探索（Stochastic Search）とは対照的です。遺伝的アルゴリズムのような確率的探索アルゴリズムは、ランダムな要素（たとえば交叉、突然変異）を利用して解の探索空間を広く探索し、多様な解を見つけることが可能です。

これに対して、決定的探索アルゴリズムは、探索パスが固定されているため、局所最適解に陥りやすいという欠点がありますが、その一方で、解が一意に定まるという利点もあります。

 

　PyGMOによるGAの適用例

PyGMOを用いてGAを適用する例を示します。

最小化する目的関数は f(x)=x^Tx で要素の二乗の総和です。 この目的関数を最小化する5次元ベクトル x=\left( x_1,x_2,x_3,x_4,x_5 \right)^T を探します。話しを簡単にするため、制約条件は設けていません。

以下、コードです。

import pygmo as pg
import numpy as np

# 問題を定義
class CustomProblem:
    # 初期化
    def __init__(self, dim):
        self.dim = dim 
    # 目的関数
    def fitness(self, x):
        return [sum(np.array(x)**2)]
    # 各変数（次元）の範囲
    def get_bounds(self):
        return ([-5]*self.dim, [5]*self.dim) 
    # 問題名
    def get_name(self):
        return "Custom Quadratic Problem"  

# 問題の次元を設定
dim = 5
prob = pg.problem(CustomProblem(dim))

# 遺伝的アルゴリズムの設定
algo = pg.algorithm(pg.sga(gen=1000))  # 遺伝的アルゴリズムのインスタンスを作成
pop = pg.population(prob, 100)  # 初期個体群を生成
pop = algo.evolve(pop)  # 進化プロセスを実行

# 結果の表示
print(f"Best solution: {pop.champion_x}")  # 最適解を表示
print(f"Best fitness: {pop.champion_f}")  # 最適解の適応度を表示

 

このコードは、PyGMOを使ってカスタムの2次関数問題を定義し、その問題に対して遺伝的アルゴリズム（SGA: Simple Genetic Algorithm）を適用して最適解を探索するプロセスを実装しています。

問題を定義

• CustomProblemクラスを定義しています。このクラスはPyGMOの問題クラスを継承していませんが、PyGMOのproblemクラスに必要なメソッドを備えているので、PyGMOで問題として扱うことができます。
  • __init__メソッドで、問題の次元（dim）を設定します。
  • fitnessメソッドでは、与えられた解xに対する目的関数の値を計算します。この場合、目的関数はxの要素の二乗和で、単純な2次関数です。
  • get_boundsメソッドでは、問題の変数が取りうる範囲を指定します。この例では、すべての変数が-5から5の範囲内であると設定しています。
  • get_nameメソッドでは、問題の名前を返します。

遺伝的アルゴリズムの設定

• algo変数に、PyGMOのsgaアルゴリズムを指定しています。ここでgen=1000は、アルゴリズムが1000世代にわたって進化を行うことを意味します。
• pop変数で、定義した問題probに対する初期個体群を生成しています。この例では、個体群のサイズを100としています。
• algo.evolve(pop)によって、初期個体群popを進化させ、問題の解を探索します。

結果の表示

• pop.champion_xで最適解、pop.champion_fでその解の適応度（目的関数の値）を表示しています。

 

以下、実行結果です。

Best solution: [ 0.00018064 -0.00453676 -0.00047497  0.00013129  0.00147305]
Best fitness: [2.30274866e-05]

 

粒子群最適化(PSO)の概要とPython実装

粒子群最適化（PSO）は、鳥や魚の群れの行動を模倣した代表的なメタヒューリスティクスです。

PSOでは、粒子と呼ばれる個体が、個々の最良解と全体の最良解の情報を共有しながら、探索空間を移動します。

 

　PSOの基本的な流れ

PSOの基本的な流れは以下の通りです。

Step.1　初期粒子群の生成
探索空間上にランダムに粒子を配置し、初期粒子群を生成します。

Step.2　粒子の位置と速度の更新
各粒子は、自身の最良解（pbest）と全体の最良解（gbest）の情報を用いて、速度\vec{v}と\vec{x}位置を更新します。更新式は以下の通りです。

速度の更新式
\displaystyle \vec{v}_{\mathrm{new}} = w \vec{v} + c_1 r_1 (\vec{p}_{\mathrm{best}} - \vec{x}) + c_2 r_2 (\vec{g}_{\mathrm{best}} - \vec{x})

位置の更新式
\displaystyle \vec{x}_{\mathrm{new}} = \vec{x} + \vec{v}_{\mathrm{new}}

• \vec{v}_{\mathrm{new}} は粒子の新しい速度ベクトル
• \vec{v} は粒子の現在の速度ベクトル
• w は慣性項（慣性の重み）
• c_1 と c_2 は加速度定数
• r_1 と r_2 は0から1の乱数
• \vec{p}_{\mathrm{best}} は粒子の最良解の位置ベクトル
• \vec{g}_{\mathrm{best}} は全体の最良解の位置ベクトル
• \vec{x} は粒子の現在の位置ベクトル
• \vec{x}_{\mathrm{new}} は粒子の新しい位置ベクトル

速度の更新式では、粒子の現在の速度に慣性項（w \vec{v}）を加え、粒子の最良解と全体の最良解に向かう方向に加速度（c_1 r_1 (\vec{p}{\mathrm{best}} - \vec{x}) と c_2 r_2 (\vec{g}{\mathrm{best}} - \vec{x})）を加えています。

位置の更新式では、粒子の現在の位置に新しい速度を加えることで、粒子の位置を更新しています。

Step.3　粒子の最良位置と全体の最良位置の更新
各粒子の新しい位置における適応度を評価し、必要に応じてpbestとgbestを更新します。

これらの操作を繰り返すことで、粒子群全体が徐々に最適解に向かって収束します。

 

　PSOの特徴

PSOには以下のような特徴があります。

鳥や魚の群れの行動を模倣
PSOは、鳥や魚の群れにおける個体間の情報共有と協調的な行動を模倣しています。

粒子の協調と情報共有
PSOでは、粒子が個々の最良解と全体の最良解の情報を共有しながら探索を行います。これにより、効率的に最適解を見つけることができます。

簡潔で実装が容易
PSOは、アルゴリズムが非常にシンプルで、実装が容易です。また、パラメータの数も比較的少ないため、チューニングが行いやすいです。

 

　PyGMOによるPSOの適用例

PyGMOを用いてPSOを適用する例を示します。

先ほどと同じ最適化問題で、最小化する目的関数は f(x)=x^Tx で要素の二乗の総和です。

以下、コードです。

import pygmo as pg
import numpy as np

# 問題を定義
class CustomProblem:
    # 初期化
    def __init__(self, dim):
        self.dim = dim
    # 目的関数
    def fitness(self, x):
        return [sum(np.array(x)**2)]
    # 各変数（次元）の範囲
    def get_bounds(self):
        return ([-5] * self.dim, [5] * self.dim) 
    # 問題名
    def get_name(self):
        return "Custom Quadratic Problem"

# 問題の次元を設定
dim = 5
prob = pg.problem(CustomProblem(dim))

# 粒子群最適化アルゴリズムの設定
algo = pg.algorithm(pg.pso(gen=1000))  # PSOアルゴリズムを設定、生成回数もここで指定しています。
pop = pg.population(prob, 100)  # 初期個体群を生成
pop = algo.evolve(pop)  # 個体群を進化させる

# 結果の表示
print(f"Best solution: {pop.champion_x}")  # 最適解を出力
print(f"Best fitness: {pop.champion_f}")  # 最適解の適応度を出力

 

このコードは、PyGMOライブラリを使用して、2次関数の最小化問題に粒子群最適化（PSO）アルゴリズムを適用するプロセスを示しています。

問題を定義

• CustomProblemクラスを定義しています。このクラスは、PyGMOの問題インターフェイスを実装しており、最適化したい具体的な問題を表します。
  • __init__メソッドで問題の次元数dimを受け取り、内部で保持しています。これは、最適化する変数の数を意味します。
  • fitnessメソッドでは、解候補x（numpy配列）の各要素の二乗和を計算しています。この値が最小化されるべき目的関数の値です。
  • get_boundsメソッドで、最適化する変数の取りうる範囲を指定しています。この例では、すべての変数が-5から5の間で変化すると設定されています。
  • get_nameメソッドでは、この問題に名前を付けています。この名前は任意です。

粒子群最適化アルゴリズムの設定

• pg.algorithmを使用して、粒子群最適化（PSO）アルゴリズムのインスタンスを作成しています。gen=1000は、アルゴリズムが1000世代にわたって進化を行うことを意味します。
• pg.populationで、定義した問題に基づいて初期個体群を生成しています。個体群のサイズは100と設定されています。これは、最適化プロセスを開始するための初期解候補の集合です。

結果の出力

• algo.evolve(pop)により、定義された問題に対してPSOアルゴリズムを適用し、個体群を進化させます。このプロセスを通じて、目的関数を最小化する解を探索します。
• pop.champion_xとpop.champion_fで、最適化プロセスを通じて見つかった最適解とその時の目的関数の値（適応度）を出力しています。これらは、PSOアルゴリズムが見つけた最良の解とその適応度を示しています。

 

以下、実行結果です。

Best solution: [ 8.62741828e-28 -1.03217592e-27  2.24642150e-28 -2.49533630e-28
 -9.34650042e-28]
Best fitness: [2.79601243e-54]

 

PyGmoで解く制約付き非線形計画問題

　取り扱う非線形計画問題

今回は、以下の非線形計画問題を扱います。前回取り扱った問題です。SciPyでは上手く解けませんでした。

\displaystyle \begin{array}{ll} \displaystyle \min_{x \in \mathbb{R}^2} \quad & f(x_0,x_1) = (1 - x_0)^2 + 100 (x_1 - x_0^2)^2 \\ \text{subject to} \quad & x_0-2x_1 - 2 \leq 0 \\ & e^{x_1}- 8 \leq 0 \\ & x_0^2 + x_1^2 - 10 \leq 0 \\ & -5 \leq x_0 \leq 5 \\ & -5 \leq x_1 \leq 5 \end{array}

 

目的関数はRosenbrock関数と呼ばれる、大域的最適解を求めるのが非常に難しい問題です。ちなみに解は、(x_0,x_1)=(1,1)です。

 

　制約条件を組み込み

最適化問題の制約条件の組み込み方には幾つか方法があります。ハードな方法とソフトな方法です。

ソフトな方法の1つに、制約条件の違反に対してペナルティを課す方法があります。

具体的には、ペナルティ関数を目的関数に加えることで、制約条件を満たさない解を避けるようにします。

今回は、このソフトな方法を採用します。

 

本来の目的関数を定義した後に、制約条件を組み込んだ目的関数（本来の目的関数＋違反ペナルティ関数）を再定義します。

以下、コードです。

# 目的関数
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約関数
def constraint_functions(x):
    c1 = x[0] - 2 * x[1] - 2
    c2 = np.exp(x[1]) - 8
    c3 = x[0]**2 + x[1]**2 - 10
    return c1, c2, c3

# 制約違反のペナルティを計算する関数
def calculate_penalty(x):
    c1, c2, c3 = constraint_functions(x)
    penalty = max(0, c1) + max(0, c2) + max(0, c3)
    return penalty

# PyGMOで使用するカスタム問題クラス
class CustomProblem:
    def fitness(self, x):
        # 目的関数値とペナルティを合計
        obj = objective(x)
        penalty = calculate_penalty(x)
        return [obj + penalty * 1e10]  # ペナルティの重みを調整

    def get_bounds(self):
        return ([-5, -5], [5, 5])

    def get_nobj(self):
        return 1

 

このコードは、目的関数、制約条件、そして制約違反のペナルティを考慮して問題を定義し、その問題を解くためのカスタム問題クラスを実装しています。

各部分について簡単に説明します。

目的関数

def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

ここで定義されているのは、ローゼンブロック関数です。

\displaystyle  f(x_0,x_1) = (1 - x_0)^2 + 100 (x_1 - x_0^2)^2

これは、非線形最適化問題でよく使用されるテスト関数の一つで、大域的最適解に向かう狭く深い谷が特徴です。最適解はx[0] = 1、x[1] = 1のときで、そのときの関数値は0です。

制約関数

def constraint_functions(x):
    c1 = x[0] - 2 * x[1] - 2
    c2 = np.exp(x[1]) - 8
    c3 = x[0]**2 + x[1]**2 - 10
    return c1, c2, c3

3つの制約条件を定義しています。これらは問題における制約を表し、最適化プロセスではこれらの制約を満たす解を探索します。

\displaystyle \begin{array}{l} x_0-2x_1 - 2 \leq 0 \\ e^{x_1}- 8 \leq 0 \\ x_0^2 + x_1^2 - 10 \leq 0 \end{array}

制約違反のペナルティ計算

def calculate_penalty(x):
    c1, c2, c3 = constraint_functions(x)
    penalty = max(0, c1) + max(0, c2) + max(0, c3)
    return penalty

制約違反のペナルティを計算しています。各制約について、制約違反がある場合（制約関数の値が正の場合）のみペナルティに加算されます。これにより、制約を満たす解が優遇されます。

PyGMOカスタム問題クラス

class CustomProblem:
    def fitness(self, x):
        obj = objective(x)
        penalty = calculate_penalty(x)
        return [obj + penalty * 1e10]  # ペナルティの重みを調整
    def get_bounds(self):
        return ([-5, -5], [5, 5])
    def get_nobj(self):
        return 1

• カスタム問題クラスです。fitnessメソッドでは、目的関数の値に制約違反のペナルティを加算しています。ペナルティには大きな重み（この場合は1e10）が掛けられており、制約違反が大きくペナルティ化されることで、制約を満たさない解が選択されにくくなります。
• get_boundsメソッドで、最適化変数の範囲を指定しています。この例では、両変数ともに-5から5の範囲内で変化すると設定されています。
• get_nobjメソッドで、問題が単一の目的関数を持つことを指定しています。

ローゼンブロック関数を目的関数とする制約付き最適化問題をPyGMOで解くための準備がこれで整いました。後は、これは最適化アルゴリズムで解くだけです。

 

　PyGMOのGAで解く

では、遺伝的アルゴリズム（GA）で解きます。

以下、コードです。

import pygmo as pg
import numpy as np

# 目的関数
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約関数
def constraint_functions(x):
    c1 = x[0] - 2 * x[1] - 2
    c2 = np.exp(x[1]) - 8
    c3 = x[0]**2 + x[1]**2 - 10
    return c1, c2, c3

# 制約違反のペナルティを計算する関数
def calculate_penalty(x):
    c1, c2, c3 = constraint_functions(x)
    penalty = max(0, c1) + max(0, c2) + max(0, c3)
    return penalty

# PyGMOで使用するカスタム問題クラス
class CustomProblem:
    def fitness(self, x):
        # 目的関数値とペナルティを合計
        obj = objective(x)
        penalty = calculate_penalty(x)
        return [obj + penalty * 1e10]  # ペナルティの重みを調整

    def get_bounds(self):
        return ([-5, -5], [5, 5])

    def get_nobj(self):
        return 1

# PyGMO問題オブジェクトを作成
prob = pg.problem(CustomProblem())

# 解くためのアルゴリズムを選択（ここでは遺伝的アルゴリズムを使用）
algo = pg.algorithm(pg.sga(gen=1000))

# 初期個体群を生成
pop = pg.population(prob, size=1000)

# 最適化を実行
pop = algo.evolve(pop)

# 結果を表示
best_sol = pop.champion_x
best_fitness = pop.champion_f
print("Best solution:", best_sol)
print("Best fitness:", best_fitness)

 

このコードを簡単に説明します。

目的関数と制約関数の定義

• objective(x)関数
  • ローゼンブロック関数を定義しています。
  • これは典型的な最適化テスト関数で、非凸で狭く深い谷を持つことから、最適化アルゴリズムの性能試験によく用いられます。
  • 最適解はx[0]=1、x[1]=1のときで、このときの目的関数の値は0です。
• constraint_functions(x)関数
  • 3つの不等式制約を定義しています。
  • これらの制約は、解候補が満たすべき条件を示しており、最適化プロセスではこれらの制約を考慮する必要があります。

制約違反のペナルティ計算

• calculate_penalty(x)関数は、与えられた解候補xについて、制約違反のペナルティを計算します。
• 制約が満たされない（つまり、制約関数の値が正である）場合、その制約違反量に応じてペナルティが加算されます。

カスタム問題クラスの定義

• CustomProblemクラスは、PyGMOで最適化を行うための問題を定義します。
• このクラスは、fitnessメソッド内で目的関数と制約違反のペナルティを合計することにより、制約付き最適化問題を処理します。
• また、変数の取りうる範囲をget_boundsメソッドで指定しています。

最適化の実行

• ここでは、遺伝的アルゴリズム（SGA: Simple Genetic Algorithm）を使用して最適化を行っています。pg.algorithm(pg.sga(gen=1000))により、1000世代にわたって進化を行う設定です。
• pg.population(prob, size=1000)により、定義した問題に対する初期個体群を1000個生成しています。
• algo.evolve(pop)で、初期個体群を用いて最適化プロセスを実行し、最適解を探索しています。

結果の表示

• pop.champion_xで最適化の結果得られた最適解の変数値を表示しています。
• pop.champion_fでそのときの目的関数の値（最良の適応度）を表示しています。

 

以下、実行結果です。

Best solution: [1.0574453  1.11842275]
Best fitness: [0.00330535]

 

最適解は(x_0,x_1)=(1,1) なので、多少誤差はありますが上手くいっていることが分かります。アルゴリズムの収束条件などを変えることでより解に近づきます。

 

　PyGMOのPSOで解く

次に、粒子群最適化（PSO）で解きます。

以下、コードです。

import pygmo as pg
import numpy as np

# 目的関数
def objective(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約関数
def constraint_functions(x):
    c1 = x[0] - 2 * x[1] - 2
    c2 = np.exp(x[1]) - 8
    c3 = x[0]**2 + x[1]**2 - 10
    return c1, c2, c3

# 制約違反のペナルティを計算する関数
def calculate_penalty(x):
    c1, c2, c3 = constraint_functions(x)
    penalty = max(0, c1) + max(0, c2) + max(0, c3)
    return penalty

# PyGMOで使用するカスタム問題クラス
class CustomProblem:
    def fitness(self, x):
        # 目的関数値とペナルティを合計
        obj = objective(x)
        penalty = calculate_penalty(x)
        return [obj + penalty * 1e10]  # ペナルティの重みを調整

    def get_bounds(self):
        return ([-5, -5], [5, 5])

    def get_nobj(self):
        return 1

# PyGMO問題オブジェクトを作成
prob = pg.problem(CustomProblem())

# 解くためのアルゴリズムを選択（ここでは粒子群最適化(PSO)を使用）
algo = pg.algorithm(pg.pso(gen=1000))

# 初期個体群を生成
pop = pg.population(prob, size=1000)

# 最適化を実行
pop = algo.evolve(pop)

# 結果を表示
best_sol = pop.champion_x
best_fitness = pop.champion_f
print("Best solution:", best_sol)
print("Best fitness:", best_fitness)

 

このコードを簡単に説明します。

目的関数と制約関数

• objective(x)関数
  • ローゼンブロック関数を定義しています。
  • これは典型的な最適化テスト関数で、非凸で狭く深い谷を持つことから、最適化アルゴリズムの性能試験によく用いられます。
  • 最適解はx[0]=1、x[1]=1のときで、このときの目的関数の値は0です。
• constraint_functions(x)関数
  • 3つの不等式制約を定義しています。
  • これらの制約は、解候補が満たすべき条件を示しており、最適化プロセスではこれらの制約を考慮する必要があります。

制約違反のペナルティ計算

• calculate_penalty(x)関数は、与えられた解候補xについて、制約違反のペナルティを計算します。
• 制約が満たされない（つまり、制約関数の値が正である）場合、その制約違反量に応じてペナルティが加算されます。

カスタム問題クラス

• CustomProblemクラスは、PyGMOで最適化を行うための問題を定義します。
• このクラスは、fitnessメソッド内で目的関数と制約違反のペナルティを合計することにより、制約付き最適化問題を処理します。
• また、変数の取りうる範囲をget_boundsメソッドで指定しています。

最適化プロセス

• pg.algorithm(pg.pso(gen=1000))によって、1000世代にわたる粒子群最適化（PSO）アルゴリズムを選択しています。PSOは、粒子の集団（個体群）を通じて解空間を探索するメタヒューリスティックな最適化アルゴリズムです。
• pg.population(prob, size=1000)で、選択した問題に対する1000個の解候補からなる初期個体群を生成しています。
• algo.evolve(pop)によって、初期個体群を進化させ、最適化を実行しています。

結果の表示

• pop.champion_xで最適化の結果得られた最適解の変数値を表示しています。
• pop.champion_fでそのときの目的関数の値（最良の適応度）を表示しています。

 

以下、実行結果です。

Best solution: [1. 1.]
Best fitness: [1.00205056e-27]

 

最適解は(x_0,x_1)=(1,1) なので、上手くいっていることが分かります。

 

多峰性関数であるAckley関数を目的関数にした例

多数の局所最適解を持つことが知られている以下のAckley関数を目的関数にし最小化する例を示します。最適解は (x_0,x_1)=(-3,4) で、最適値は 0 です。

 

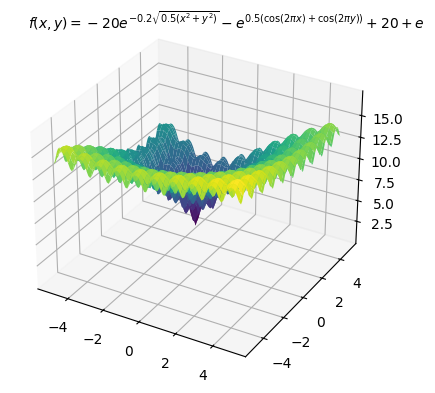
　PyGMOのGAで解く

では、遺伝的アルゴリズム（GA）で解きます。変数の上下限制約のみ入れています。

以下、コードです。

import pygmo as pg
import numpy as np

# 目的関数の定義
def objective(x):
    a = 20
    b = 0.2
    c = 2 * np.pi
    n = len(x)
    x_offset = np.array([x[0] + 3, x[1] - 4])
    sum_sq_term = -a * np.exp(-b * np.sqrt(sum(x_offset**2) / n))
    cos_term = -np.exp(sum(np.cos(c * x_offset) / n))
    return sum_sq_term + cos_term + a + np.e

# PyGMOで使用するカスタム問題クラス
class CustomProblem:
    def fitness(self, x):
        # 目的関数値
        obj = objective(x)
        return [obj]
        return objective

    def get_bounds(self):
        return ([-5, -5], [5, 5])

    def get_nobj(self):
        return 1

# PyGMO問題オブジェクトを作成
prob = pg.problem(CustomProblem())

# 解くためのアルゴリズムを選択（ここでは遺伝的アルゴリズムを使用）
algo = pg.algorithm(pg.sga(gen=1000))

# 初期個体群を生成
pop = pg.population(prob, size=1000)

# 最適化を実行
pop = algo.evolve(pop)

# 結果を表示
best_sol = pop.champion_x
best_fitness = pop.champion_f
print("Best solution:", best_sol)
print("Best fitness:", best_fitness)

 

以下、実行結果です。

Best solution: [-3.00031396  3.99987634]
Best fitness: [0.00095743]

 

最適解は(x_0,x_1)=(-3,4) なので、多少誤差はありますが上手くいっていることが分かります。アルゴリズムの収束条件などを変えることでより解に近づきます。

 

　PyGMOのPSOで解く

次に、粒子群最適化（PSO）で解きます。

以下、コードです。

import pygmo as pg
import numpy as np

# 目的関数の定義
def objective(x):
    a = 20
    b = 0.2
    c = 2 * np.pi
    n = len(x)
    x_offset = np.array([x[0] + 3, x[1] - 4])
    sum_sq_term = -a * np.exp(-b * np.sqrt(sum(x_offset**2) / n))
    cos_term = -np.exp(sum(np.cos(c * x_offset) / n))
    return sum_sq_term + cos_term + a + np.e

# PyGMOで使用するカスタム問題クラス
class CustomProblem:
    def fitness(self, x):
        # 目的関数値
        obj = objective(x)
        return [obj]
        return objective

    def get_bounds(self):
        return ([-5, -5], [5, 5])

    def get_nobj(self):
        return 1

# PyGMO問題オブジェクトを作成
prob = pg.problem(CustomProblem())

# 解くためのアルゴリズムを選択（ここでは粒子群最適化(PSO)を使用）
algo = pg.algorithm(pg.pso(gen=1000))

# 初期個体群を生成
pop = pg.population(prob, size=1000)

# 最適化を実行
pop = algo.evolve(pop)

# 結果を表示
best_sol = pop.champion_x
best_fitness = pop.champion_f
print("Best solution:", best_sol)
print("Best fitness:", best_fitness)

 

以下、実行結果です。

Best solution: [-3.  4.]
Best fitness: [4.4408921e-16]

 

最適解は(x_0,x_1)=(-3,4) なので、上手くいっていることが分かります。

 

メタヒューリスティクスの特徴とチューニング

メタヒューリスティクスは、大域的最適化に有効なアプローチですが、その性能はアルゴリズムの選択とパラメータ設定に大きく依存します。

ここでは、メタヒューリスティクスの特徴と、チューニングのコツについて説明します。

 

　メタヒューリスティクスの特徴

メタヒューリスティクスには、以下のような長所があります。

大域的最適解の探索能力
メタヒューリスティクスは、局所解からの脱出メカニズムを持つため、大域的最適解の探索に適しています。

問題依存性の低さ
メタヒューリスティクスは、問題の特性に依存しない一般的な探索戦略を提供するため、様々な問題に適用可能です。

 

一方で、メタヒューリスティクスには以下のような短所もあります。

収束速度と解の質のトレードオフ
メタヒューリスティクスは、大域的探索と局所的探索のバランスを取る必要があるため、収束速度と解の質はトレードオフの関係になります。

アルゴリズムパラメータの設定の難しさ
メタヒューリスティクスの性能は、アルゴリズムパラメータの設定に大きく依存します。適切なパラメータを見つけるためには、試行錯誤が必要です。

 

　メタヒューリスティクスの適用のポイント

メタヒューリスティクスを実際の問題に適用する際には、以下のようなポイントに注意が必要です。

問題の適切な定式化
メタヒューリスティクスを適用するためには、問題を適切に定式化する必要があります。目的関数や制約条件の設定が不適切だと、良い解が得られない可能性があります。

アルゴリズムの選択
問題の特性に合ったアルゴリズムを選択することが重要です。例えば、組合せ最適化問題にはACOが、連続最適化問題にはDEが適しています。

パラメータのチューニング
アルゴリズムのパラメータは、問題ごとに適切にチューニングする必要があります。チューニングには時間がかかりますが、探索性能を大きく向上させることができます。

結果の評価と解釈
メタヒューリスティクスは確率的な手法であるため、結果の評価と解釈には注意が必要です。複数回の試行を行い、統計的な評価を行うことが重要です。

 

　メタヒューリスティクスのチューニング

メタヒューリスティクスの性能を最大限に引き出すためには、以下のようなポイントを押さえたチューニングが重要です。

パラメータの影響の理解
各パラメータが探索性能にどのような影響を与えるかを理解することが重要です。例えば、GAの交叉率を上げると探索の多様性が増しますが、突然変異率を上げすぎると収束が遅くなります。

適応的なパラメータ調整
探索の過程に応じてパラメータを適応的に調整することで、探索性能を向上させることができます。例えば、探索の初期段階では多様性を重視し、後期段階では収束を重視するなどの戦略が考えられます。

複数のアルゴリズムの組み合わせ
複数のメタヒューリスティクスを組み合わせることで、それぞれの長所を活かした探索が可能になります。例えば、PSOとGAを組み合わせることで、PSOの収束速度とGAの探索の多様性を両立させることができます。

問題の特性に合わせたカスタマイズ
問題の特性を考慮して、アルゴリズムをカスタマイズすることが重要です。例えば、制約条件の取り扱い方や、解の表現方法などを工夫することで、探索性能を向上させることができます。

 

まとめ

今回は、Pythonを使った非線形計画問題の大域的最適化について、メタヒューリスティクスを中心に解説してきました。

メタヒューリスティクスは、大域的最適化に有効なアプローチであり、代表的な手法としてGAとPSOを紹介しました。

また、PyGMOは様々なメタヒューリスティクスを提供する強力なPythonライブラリであることを示しました。

ただし、メタヒューリスティクスの性能は、アルゴリズムの選択とパラメータ設定に大きく依存するため、適切なチューニングと適用のポイントに注意が必要です。

次回は、決定論的な大域的最適化手法について解説します。お楽しみに！

【Pythonで学ぶ】非線形計画問題の大域的最適化に挑む！– 【第3回】Pythonによる大域的最適化手法の実装（決定論的手法編） –