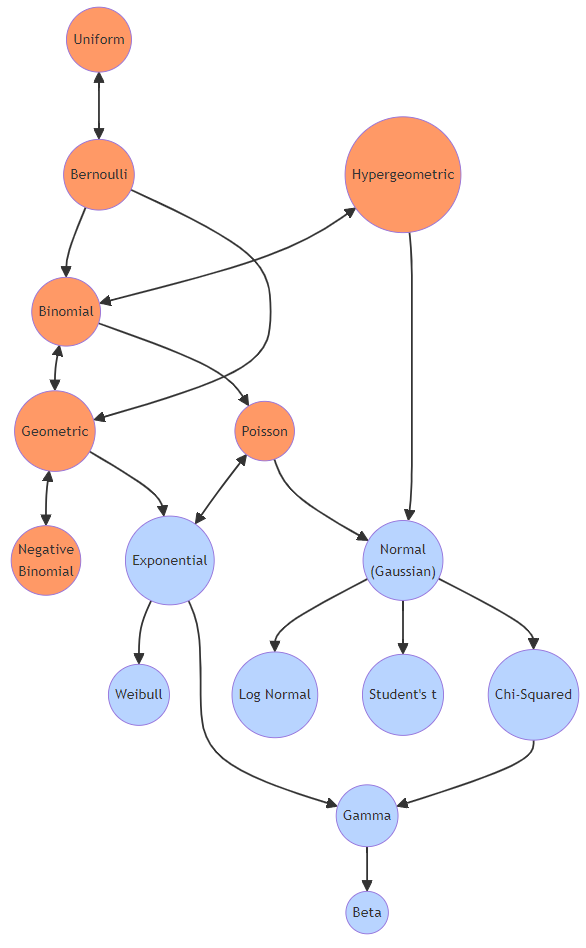
前回のブログでは、以下の確率分布の基礎から離散分布のビジネス応用について解説しました。
- 離散一様分布
- 二項分布
- ポアソン分布
- 幾何分布
- 負の二項分布
- 超幾何分布
それぞれの分布について、定義、確率関数、期待値と分散、そしてビジネス応用例を紹介しました。
離散分布は、例えばマーケティングキャンペーンの成功率や製品の品質管理など、様々なビジネスシーンで活用されています。
今回は、連続分布に焦点を当て、その基本的な概念からビジネスでの応用例までを簡単に紹介します。
連続分布は、データ分析やモデル構築において欠かせない重要なツールです。
Contents [hide]
- 連続分布とは
- 連続分布の定義
- 離散分布との違い
- 連続分布の重要性
- 主要な連続分布の一覧
- 連続一様分布
- 連続一様分布とは
- 確率密度関数
- 期待値と分散
- ビジネス活用事例
- 背景
- 一様分布を選ぶ理由
- 実施手順
- 期待される効果
- 指数分布
- 指数分布とは
- 確率密度関数
- 期待値と分散
- ビジネス活用事例
- 背景
- 指数分布を選ぶ理由
- 実施手順
- 期待される効果
- 正規分布
- 正規分布とは
- 確率密度関数
- 期待値と分散
- ビジネス活用事例
- 背景
- 正規分布を選ぶ理由
- 実施手順
- 期待される効果
- カイ二乗分布
- カイ二乗分布とは
- 確率密度関数
- 期待値と分散
- ビジネス活用事例
- 背景
- カイ二乗分布を選ぶ理由
- 実施手順
- 期待される効果
- ガンマ分布
- ガンマ分布とは
- 確率密度関数
- 期待値と分散
- ビジネス活用事例
- 背景
- ガンマ分布を選ぶ理由
- 実施手順
- 期待される効果
- ベータ分布
- ベータ分布とは
- 確率密度関数
- 期待値と分散
- ビジネス活用事例
- 背景
- ベータ分布を選ぶ理由
- 実施手順
- 期待される効果
- 今回のまとめ
連続分布とは
連続分布の定義
連続分布とは、確率変数が連続的に取りうる値を表す確率分布です。
これは、変数が特定の範囲内で無限の値を取り得る場合に適用されます。
例えば、身長や体重のような物理的な量は連続分布に従います。
連続分布の特徴は、個々の値の確率は0であり、特定の範囲に属する確率が重要となる点です。
離散分布との違い
離散分布は、変数が取りうる値が個別に区切られている場合に用いられます。
例えば、サイコロの目のように、1、2、3、4、5、6という具体的な値を取ります。
一方、連続分布では、変数が取りうる値は無限に存在し、その範囲内で任意の値を取ることができます。
確率密度関数(PDF)を用いて、特定の範囲内の確率を計算します。
連続分布の重要性
連続分布は、現実世界の多くのデータ分析やモデル構築において非常に重要です。
例えば、金融市場での価格変動、製造業での測定誤差、医学における生体データの解析など、多くの分野で連続分布が利用されています。
連続分布を理解することで、データの特性を正確に把握し、適切な統計的手法を適用することが可能になります。
主要な連続分布の一覧
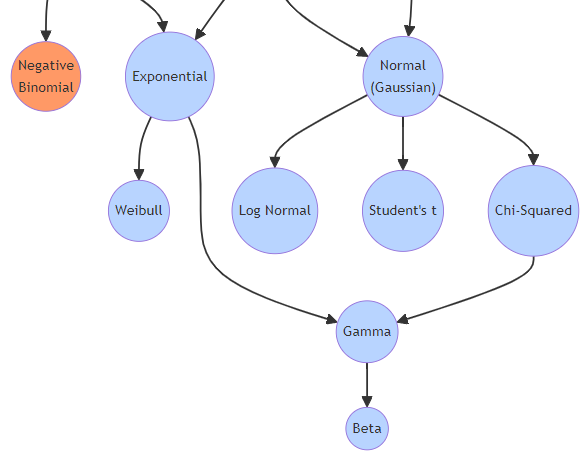
連続分布には多くの種類があり、それぞれ異なる特性を持っています。
以下に、ビジネスでよく利用される主要な連続分布を紹介します。
| 分布名 | 定義 | 例 |
|---|---|---|
| 連続一様分布 Uniform |
すべての区間が等しい確率で発生する分布 | 0から1までの範囲でランダムに値を取る場合 |
| 指数分布 Exponential |
ランダムな出来事の発生間隔をモデル化する分布 | 電話センターでの次の電話がかかってくるまでの時間 |
| 正規分布 Normal |
多くの自然現象や測定データに見られるベル型の分布 | 身長や体重、テストの点数 |
| カイ二乗分布 Chi-Squared |
確率変数が自由度の数だけの独立した標準正規分布に従う場合に用いられる分布 | 統計的検定やモデルの適合度検定 |
| ガンマ分布 Gamma |
指数分布を一般化した分布。待ち時間や寿命などをモデル化する | 機械の故障までの時間やプロジェクト完了までの時間 |
| ベータ分布 Beta |
確率変数が0から1の間にある場合に用いられる分布 | 確率の分布を表す場合、ベイズ統計での事前分布 |
連続一様分布
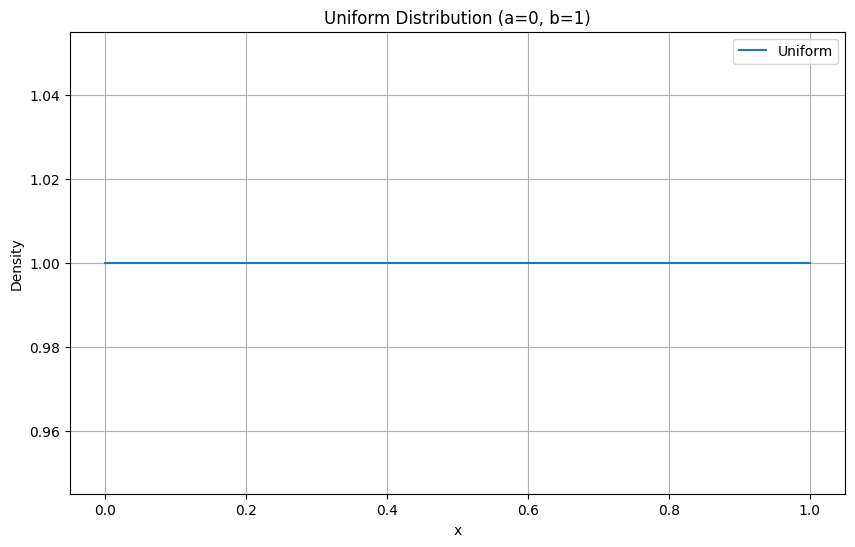
連続一様分布とは
連続一様分布は、ある区間内のすべての値が同じ確率で現れる分布です。
この分布では、特定の範囲
例えば、乱数生成やシミュレーションにおいて広く利用されます。
確率密度関数
連続一様分布の確率密度関数 (PDF) は次のように定義されます。
期待値と分散
期待値 (E(X))
分散 (V(X))
ビジネス活用事例
背景
ある企業が新しい市場に進出しようとしています。
この市場では、未知の要因が多いため、売上の予測が困難です。
市場のリスクを評価するために、連続一様分布を用いて売上の範囲を予測します。
一様分布を選ぶ理由
シンプルな仮定
一様分布は、すべての値が等しい確率で発生するというシンプルな仮定に基づいています。これにより、複雑なデータが不足している場合や、初期のリスク評価に適しています。
不確実性の反映
未知の市場や新しいビジネス領域では、データが十分に揃っていないことが多いため、各結果が均等に発生するという仮定が適しています。これにより、不確実性を均等に扱うことができます。
初期モデルの構築
一様分布は初期モデルの構築に適しており、追加のデータが得られるまでの間、合理的な予測を提供します。将来的には、より詳細なデータに基づいてモデルを改善することが可能です。
実施手順
ステップ1:データ収集
過去の市場データや類似市場のデータを収集し、売上の範囲 a と b を設定します。
ステップ2:モデル構築
連続一様分布を用いて売上の予測モデルを構築します。
ステップ3:リスク評価
モデルに基づき、売上が特定の範囲に収まる確率を評価し、リスクを分析します。
ステップ4:戦略策定
リスク評価の結果を基に、進出戦略を策定します。例えば、最悪のケースに備えたリスクヘッジ策を講じます。
期待される効果
リスクの定量化
売上の範囲を設定することで、リスクを定量的に評価できます。
戦略的意思決定
リスク評価の結果を基に、より適切な市場進出戦略を策定できます。
予測精度の向上
市場の不確実性を考慮した予測モデルにより、予測精度が向上します。
指数分布
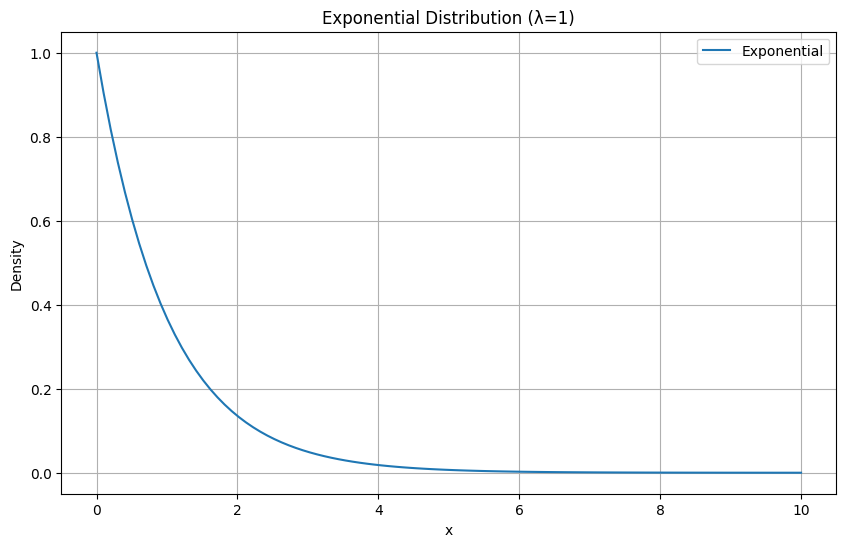
指数分布とは
指数分布は、ランダムな出来事の発生間隔をモデル化するための分布です。
特に、ポアソン過程における事象間の時間間隔を表す場合に用いられます。
例えば、一定の時間内に発生する電話の呼び出しや機械の故障までの時間などが指数分布に従います。
確率密度関数
指数分布の確率密度関数 (PDF) は次のように定義されます。
期待値と分散
期待値 (E(X))
分散 (V(X))
ビジネス活用事例
背景
あるコールセンターが、顧客からの問い合わせに対する待ち時間を短縮しようとしています。
待ち時間の予測と管理を効率化するために、指数分布を用いて待ち時間をモデル化します。
指数分布を選ぶ理由
メモリーレス性
指数分布はメモリーレス特性を持っており、これにより前の出来事からの経過時間が次の出来事の発生に影響を与えないことを示します。コールセンターの問い合わせ間隔など、過去の問い合わせのタイミングが次の問い合わせのタイミングに影響しない場合に適しています。
自然な適合
コールセンターやサービス業における顧客の問い合わせや到着時間は、多くの場合、ランダムであり、一定の平均発生率に従います。このような状況では、指数分布が自然にデータに適合します。
単純で効果的なモデリング
指数分布は単純でありながら、実用的なモデリングが可能です。少ないパラメータで待ち時間の予測を行うことができるため、実装が容易です。
実施手順
ステップ1:データ収集
過去の問い合わせデータを収集し、各問い合わせの間隔時間を記録します。
ステップ2:モデル構築
収集したデータを基に、指数分布のレートパラメータ λ を推定します。
ステップ3:待ち時間の予測
推定されたレートパラメータを用いて、次の問い合わせまでの待ち時間を予測します。
ステップ4:リソース管理
予測された待ち時間に基づいて、スタッフのシフトやリソースの最適化を行います。
期待される効果
待ち時間の短縮
待ち時間の予測精度が向上することで、顧客の待ち時間を短縮できます。
リソースの最適化
適切なスタッフ配置により、コスト削減とサービス品質の向上が可能です。
顧客満足度の向上
迅速な対応により、顧客満足度が向上します。
正規分布
正規分布とは
正規分布(Normal Distribution)は、自然現象や人間の行動など、多くの現象に広く見られる分布です。
ベル型の曲線を描くこの分布は、平均値を中心に対称に広がり、多くの統計分析の基礎となります。
確率密度関数
正規分布の確率密度関数 (PDF) は次のように定義されます。
期待値と分散
期待値 (E(X))
分散 (V(X))
ビジネス活用事例
背景
正規分布(Normal Distribution)は、自然現象や人間の行動など、多くの現象に広く見られる分布です。
ベル型の曲線を描くこの分布は、平均値を中心に対称に広がり、多くの統計分析の基礎となります。
正規分布を選ぶ理由
自然現象の多くが正規分布に従う
正規分布は、多くの自然現象や人間の行動に見られるパターンです。これは、中心極限定理によって、独立したランダム変数の和が正規分布に近づくためです。例えば、製品の寸法や重量、売上データなど、多くのデータセットが正規分布に近似されます。
データの対称性と中央集中性
正規分布は平均値を中心に対称であり、データが中心に集中している場合に適しています。製品の品質データや売上データは、一般的に中央に集中する傾向があり、この特性が正規分布に適合します。
異常値検出の容易さ
正規分布を用いることで、データの異常値を検出しやすくなります。標準偏差を利用して、平均からの逸脱がどの程度異常であるかを定量的に評価できます。
広範な統計手法の適用
多くの統計手法や品質管理手法が正規分布を前提としています。正規分布に従うデータであれば、これらの手法を適用することで、効果的な分析が可能になります。
実施手順
ステップ1:データ収集
過去の品質検査データと売上データを収集し、各データの平均値 (μ) と標準偏差 (σ) を算出します。
ステップ2:モデル構築
正規分布を用いて品質データと売上データをモデル化し、確率密度関数を構築します。
ステップ3:異常値の検出
モデルを用いて、品質データの異常値を検出し、不良品の早期発見を行います。
ステップ4:売上予測
売上データを基に、正規分布モデルを用いて将来の売上を予測します。
ステップ5:戦略策定
異常値の検出結果と売上予測を基に、品質改善策やマーケティング戦略を策定します。
期待される効果
品質管理の強化
正規分布を用いた異常値検出により、不良品の早期発見と品質管理の強化が可能になります。
予測精度の向上
売上予測モデルの精度が向上し、適切な在庫管理や生産計画が立てられます。
コスト削減
品質管理の強化により、不良品の削減と関連コストの削減が期待されます。
カイ二乗分布
カイ二乗分布とは
カイ二乗分布(Chi-Squared Distribution)は、確率変数が独立した標準正規分布に従う場合の二乗和として定義されます。
この分布は、統計的検定やデータの適合度検定などに広く使用されます。
確率密度関数
カイ二乗分布の確率密度関数 (PDF) は次のように定義されます。
期待値と分散
期待値 (E(X))
分散 (V(X))
ビジネス活用事例
背景
ある小売業者が、新しいマーケティングキャンペーンの効果を評価するために、顧客の購買データを分析しています。
カイ二乗検定を用いて、キャンペーン前後の購買行動の変化が統計的に有意かどうかを判断します。
カイ二乗分布を選ぶ理由
カテゴリー変数の分析
カイ二乗検定は、カテゴリー変数の独立性を評価するために広く使用されます。例えば、顧客の購買データを製品カテゴリーや購入頻度などのカテゴリーごとに整理し、それらの変化を評価するのに適しています。
適合度検定
観測データが期待される分布にどの程度適合しているかを評価するためにカイ二乗検定が用いられます。これにより、キャンペーンの前後で購買行動に有意な変化があるかを判断できます。
標準正規分布に基づく
カイ二乗分布は、標準正規分布に従う独立した変数の二乗和として定義されます。これにより、標準化されたデータを使って簡単に検定を行うことができます。
自由度の調整
カイ二乗分布は自由度を持ち、データのサンプルサイズやカテゴリー数に応じて適用範囲が広いです。これにより、実際のビジネスデータに柔軟に対応できます。
実施手順
ステップ1:データ収集
キャンペーン前後の購買データを収集し、各カテゴリー(例:製品タイプ、購入頻度など)ごとに整理します。
ステップ2:期待値の計算
各カテゴリーの期待される購買数を計算します。期待値は、キャンペーン前のデータに基づきます。
ステップ3:カイ二乗検定の実施
観測データと期待値を比較し、カイ二乗統計量を計算します。
ステップ4:有意性の判断
カイ二乗分布を用いて、統計量の有意性を判断します。特定の信頼水準で、有意な差があるかどうかを確認します。
期待される効果
キャンペーン効果の定量化
カイ二乗検定により、キャンペーンの効果を統計的に有意に評価できます。
データ駆動型の意思決定
統計的な検証に基づいたデータ分析により、より正確なマーケティング戦略を策定できます。
リソースの最適配分
有意性が確認された場合、リソースを効果的に配分し、ROI(投資収益率)を最大化します。
ガンマ分布
ガンマ分布とは
ガンマ分布(Gamma Distribution)は、待ち時間や寿命などのデータをモデル化するための分布です。
特に、指数分布の一般化として知られ、幅広い形状を持つため、さまざまな応用が可能です。
確率密度関数
ガンマ分布の確率密度関数 (PDF) は次のように定義されます。
ここで、
期待値と分散
期待値 (E(X))
分散 (V(X))
ビジネス活用事例
背景
あるIT企業が、ソフトウェア開発プロジェクトの完了までの時間を予測し、リソースを効率的に配分したいと考えています。
ガンマ分布を用いて、プロジェクトのリードタイムをモデル化し、予測精度を向上させます。
ガンマ分布を選ぶ理由
待ち時間や寿命データのモデル化
ガンマ分布は、待ち時間や寿命のデータをモデル化するのに適しています。これは、プロジェクト完了までの時間や製品の寿命などのデータに対して自然に適合します。
柔軟な形状
ガンマ分布は形状パラメータ k と尺度パラメータ θ により、幅広い形状を取ることができます。これにより、データの特性に合わせて柔軟にモデルを構築できます。
指数分布の一般化
ガンマ分布は指数分布の一般化であり、複数の独立した指数分布に従う変数の和としても表現されます。これにより、プロジェクトの各フェーズの完了時間をモデル化するのに適しています。
実施手順
ステップ1:データ収集
過去のプロジェクトデータを収集し、各プロジェクトのリードタイムを記録します。
ステップ2:モデル構築
収集したデータを基に、ガンマ分布の形状パラメータ k と尺度パラメータ θ を推定します。
ステップ3:リードタイムの予測
推定されたパラメータを用いて、現在進行中のプロジェクトのリードタイムを予測します。
ステップ4:リソース管理
予測されたリードタイムに基づいて、適切なリソースの割り当てやスケジュールの調整を行います。
期待される効果
予測精度の向上
ガンマ分布を用いることで、プロジェクト完了までの時間の予測精度が向上します。
効率的なリソース配分
予測されたリードタイムに基づいてリソースを効率的に配分することで、コスト削減と生産性の向上が期待されます。
プロジェクト管理の改善
リードタイム予測に基づくスケジュール調整により、プロジェクトの遅延を防止し、納期遵守率を向上させます。
ベータ分布
ベータ分布とは
ベータ分布(Beta Distribution)は、確率変数が0から1の間にある場合に適用される分布です。
主に、確率や割合をモデル化するために使用されます。ベータ分布は、2つのパラメータ(形状パラメータ
確率密度関数
ベータ分布の確率密度関数 (PDF) は次のように定義されます。
ここで、
期待値と分散
期待値 (E(X))
分散 (V(X))
ビジネス活用事例
背景
あるマーケティングチームが、新製品の市場浸透率を予測し、販売戦略を策定するためにベータ分布を使用しています。
市場浸透率のような確率や割合をモデル化する際に、ベータ分布は非常に適しています。
ベータ分布を選ぶ理由
確率や割合のモデリング
ベータ分布は、確率変数が0から1の間にある場合に適しています。例えば、市場浸透率や製品の故障確率などをモデル化する際に利用できます。
柔軟な形状
ベータ分布は2つの形状パラメータ (α と β) により、多様な形状を取ることができます。これにより、データの特性に合わせて適切なモデルを構築できます。
ベイズ推定
ベータ分布はベイズ推定において、事前分布として広く使用されます。これにより、事後分布の計算が簡便になり、確率モデルの更新が容易です。
実施手順
ステップ1:データ収集
過去の販売データや市場調査データを収集し、市場浸透率に関する情報を整理します。
ステップ2:事前分布の設定
ベータ分布を事前分布として設定し、初期の形状パラメータ α と β を決定します。
ステップ3:データに基づく更新
新しいデータが得られるたびに、ベイズ推定を用いて形状パラメータを更新し、事後分布を計算します。
ステップ4:確率モデルの構築
更新されたベータ分布に基づいて、市場浸透率の予測モデルを構築します。
ステップ5:戦略策定
予測モデルに基づき、販売戦略やマーケティングキャンペーンを策定します。
期待される効果
予測精度の向上
ベータ分布を用いることで、確率や割合の予測精度が向上します。
動的なモデル更新
ベイズ推定を利用することで、データに基づく動的なモデル更新が可能となり、迅速な意思決定が可能です。
リスク管理の強化
市場浸透率の予測精度が向上することで、リスク管理が強化され、効果的な戦略策定が可能です。
今回のまとめ
今回は、連続分布に焦点を当て、その基本的な概念からビジネスでの応用例までを簡単に紹介しました。
- 連続一様分布
- 指数分布
- 正規分布
- カイ二乗分布
- ガンマ分布
- ベータ分布
連続分布は、ビジネスのさまざまな分野で欠かせないツールです。
正規分布や指数分布、ガンマ分布など、連続分布を活用することで、データの特性を正確に把握し、精度の高い予測や効果的な意思決定が可能になります。
これにより、リスクの管理や品質の向上、リソースの最適化など、多くのメリットを享受できます。
ビッグデータや機械学習の進展により、より複雑なデータ解析や高度なモデリングが求められる中で、連続分布の理解と活用はますます重要になります。
特に、リアルタイムデータの解析や予測、異常検知などの分野では、連続分布を基盤とした技術が不可欠です。
確率分布の基礎とビジネス応用についての理解を深めることは、現代のデータドリブンなビジネス環境において極めて重要です。
今回のブログを通じて、連続分布の基本的な概念から具体的なビジネス応用例までを学びました。今後もこの知識を活用し、データ解析の精度を高め、ビジネスの成功に繋げていただければ幸いです。

