Python 時系列分析 1,000本ノック– ノック61: 時系列モデル –

問題
答え
解説

次の Python コードは、どの種類のモデルを実装していますか？

Python コード:

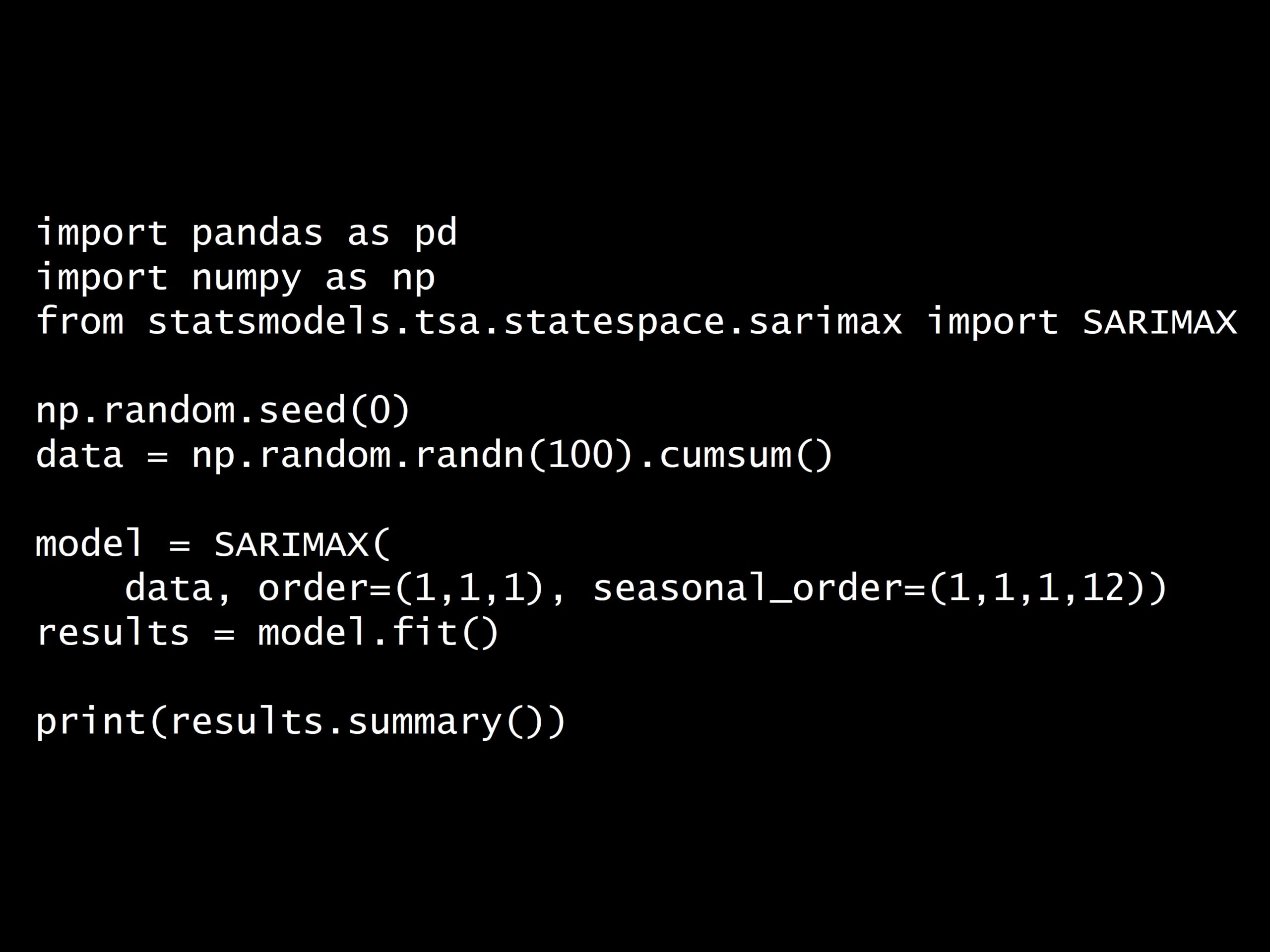
import pandas as pd
import numpy as np
from statsmodels.tsa.statespace.sarimax import SARIMAX

np.random.seed(0)
data = np.random.randn(100).cumsum()

model = SARIMAX(
    data, order=(1,1,1), seasonal_order=(1,1,1,12))
results = model.fit()

print(results.summary())

回答の選択肢:

(A) 単純移動平均モデル
(B) 調整移動平均モデル
(C) 自己回帰移動平均モデル
(D) 状態空間モデル

出力例:

                                     SARIMAX Results                                      
==========================================================================================
Dep. Variable:                                  y   No. Observations:                  100
Model:             SARIMAX(1, 1, 1)x(1, 1, 1, 12)   Log Likelihood                -132.907
Date:                            Mon, 08 Jul 2024   AIC                            275.813
Time:                                    09:43:55   BIC                            288.143
Sample:                                         0   HQIC                           280.778
                                            - 100                                         
Covariance Type:                              opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1          0.9830      0.129      7.645      0.000       0.731       1.235
ma.L1         -0.9136      0.109     -8.350      0.000      -1.128      -0.699
ar.S.L12       0.1951      0.212      0.919      0.358      -0.221       0.611
ma.S.L12      -0.9992     70.641     -0.014      0.989    -139.452     137.454
sigma2         0.9865     69.503      0.014      0.989    -135.236     137.209
===================================================================================
Ljung-Box (L1) (Q):                   0.12   Jarque-Bera (JB):                 0.39
Prob(Q):                              0.73   Prob(JB):                         0.82
Heteroskedasticity (H):               0.67   Skew:                            -0.15
Prob(H) (two-sided):                  0.29   Kurtosis:                         2.85
===================================================================================

正解: (D)

回答の選択肢:

(A) 単純移動平均モデル
(B) 調整移動平均モデル
(C) 自己回帰移動平均モデル
(D) 状態空間モデル

コードの解説

このコードは、状態空間モデルの1つである SARIMAX（Seasonal AutoRegressive Integrated Moving Average with eXogenous regressors）モデルを使用して時系列データを分析する方法を示しています。

import pandas as pd
import numpy as np
from statsmodels.tsa.statespace.sarimax import SARIMAX

np.random.seed(0)
data = np.random.randn(100).cumsum()

model = SARIMAX(
    data, order=(1,1,1), seasonal_order=(1,1,1,12))
results = model.fit()

print(results.summary())

詳しく説明します。

データを生成しdataに格納します。ランダムな値の累積和を持つ時系列データです。

np.random.seed(0)
data = np.random.randn(100).cumsum()

SARIMAXモデルを構築します。結果は、resultsに格納します。

model = SARIMAX(
    data, order=(1,1,1), seasonal_order=(1,1,1,12))
results = model.fit()

モデルのサマリーを表示します。これには、係数の推定値、標準誤差、z値、p値などが含まれます。

print(results.summary())

                                     SARIMAX Results                                      
==========================================================================================
Dep. Variable:                                  y   No. Observations:                  100
Model:             SARIMAX(1, 1, 1)x(1, 1, 1, 12)   Log Likelihood                -132.907
Date:                            Mon, 08 Jul 2024   AIC                            275.813
Time:                                    09:43:55   BIC                            288.143
Sample:                                         0   HQIC                           280.778
                                            - 100                                         
Covariance Type:                              opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1          0.9830      0.129      7.645      0.000       0.731       1.235
ma.L1         -0.9136      0.109     -8.350      0.000      -1.128      -0.699
ar.S.L12       0.1951      0.212      0.919      0.358      -0.221       0.611
ma.S.L12      -0.9992     70.641     -0.014      0.989    -139.452     137.454
sigma2         0.9865     69.503      0.014      0.989    -135.236     137.209
===================================================================================
Ljung-Box (L1) (Q):                   0.12   Jarque-Bera (JB):                 0.39
Prob(Q):                              0.73   Prob(JB):                         0.82
Heteroskedasticity (H):               0.67   Skew:                            -0.15
Prob(H) (two-sided):                  0.29   Kurtosis:                         2.85
===================================================================================

状態空間モデルとは？