データの海に潜む異彩の輝き、それが「外れ値」です。
多くの人がノイズとして見過ごしがちなこの存在こそ、実はデータ分析における貴重な宝石なのです。
ビッグデータ時代の今だからこそ注目すべき外れ値の重要性と、それを見つけ出すための様々な手法(統計的手法から最新の機械学習アルゴリズムまで)をご紹介します。
今回は、データ分析における重要なテーマである外れ値検出について、基本的な概念から高度な手法まで幅広くお話しします。
Contents
- はじめに
- 外れ値検出の4つのカテゴリー
- 統計的手法
- クラスタリング手法(近接性ベース)
- 時系列分析手法
- 機械学習手法
- 統計的手法:箱ひげ図とIQR法
- 概要
- 外れ値の定義
- 利点と注意点
- 適用例1:異常な取引や市場動向の検出
- 適用例2:製造プロセスにおける異常値の特定
- 適用例3:異常気象や汚染レベルの検出
- 近接性ベースの手法:K近傍法
- 概要
- 検知ステップ
- 利点と注意点
- 適用例1:不正取引の検出、リスク評価
- 適用例2:異常な検査結果や症状の特定
- 適用例3:異常なネットワークトラフィックの検出
- 適用例4:製品品質の異常値検出
- 時系列データにおける外れ値検出
- 概要
- 外れ値検出の手順
- その他の時系列外れ値検出手法
- 利点と注意点
- 適用例1:株価や為替レートの急激な変動の特定
- 適用例2:機器の異常動作や故障の早期発見
- 適用例3:サイトへの異常アクセスやDDoS攻撃の検出
- 適用例4:異常気象や気候変動の兆候の特定
- 機械学習を用いた外れ値検出:Isolation Forest
- 概要
- 外れ値検知アルゴリズム
- 利点と注意点
- 適用例1:異常なネットワークトラフィックや不正アクセスの検出
- 適用例2:不正取引の検出、リスク評価
- 適用例3:製品品質の異常値検出、設備の故障予測
- 適用例4:画像診断における異常な所見の検出、稀少な症例の特定
- 今回のまとめ
はじめに
私たちの周りには、日々膨大なデータが生成されています。
そのデータの海の中で、時として「普通」から大きく外れた値に遭遇することがあります。これらの値、すなわち「外れ値」は、多くの場合、データ分析において重要な意味を持っています。
外れ値とは、簡単に言えば「他の観測値と著しく異なるデータポイント」のことです。
統計学的には、データの分布から大きく逸脱した値として定義されます。例えば、クラスの平均身長が170cmの中で、220cmという身長データがあれば、それは外れ値と考えられるでしょう。
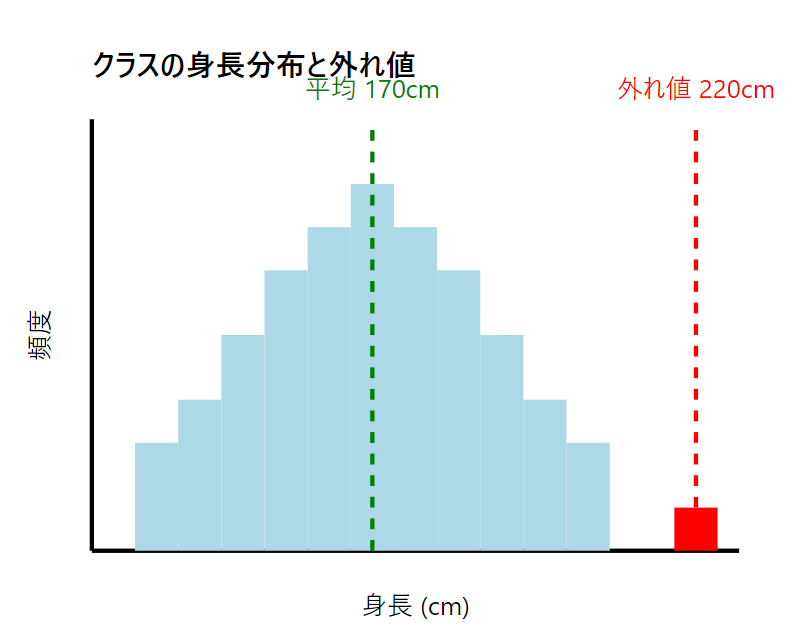
一見すると、これらの外れ値は「誤差」や「ノイズ」として扱われがちです。しかし、実はこれらの値こそが、重要な洞察や意味のある事象を示している可能性が高いのです。
例えば……
- 金融分野では、通常とは異なる取引パターンが不正行為を示唆するかもしれません。
- 医療分野では、通常の範囲を超えた検査結果が重大な健康問題を示すサインかもしれません。
- 製造業では、製品の品質データにおける外れ値が、製造プロセスの問題点を明らかにするかもしれません。
このように、外れ値は単なる「異常」ではなく、重要な情報源となり得るのです。そのため、データ分析において外れ値を適切に検出し、解釈することは非常に重要です。
しかし、外れ値の検出は簡単ではありません。データの性質や分析の目的によって、適切な検出方法は異なります。また、真の外れ値と単なる測定誤差を区別することも重要です。
外れ値検出の4つのカテゴリー
外れ値検出の手法は多岐にわたりますが、大きく分けて4つのカテゴリーに分類することができます。
これらの手法は、データの性質や分析の目的に応じて使い分けることが重要です。ここでは、それぞれのカテゴリーの特徴と適用場面について解説します。
統計的手法
統計的手法は、データの分布や統計量を利用して外れ値を検出します。この手法の最大の利点は、データの基本的な特性を理解しやすく、結果の解釈が比較的容易なことです。
特徴
- データの分布を基に判断
- 比較的シンプルで解釈しやすい
- 大規模なデータセットにも適用可能
代表的な手法
- 箱ひげ図(Box Plot)とIQR法
- Z-スコア法
- グラブス検定
適用例
- 金融データの異常取引検出
- 製造業の品質管理
- 気象データの異常値検出
クラスタリング手法(近接性ベース)
クラスタリング手法は、データポイント間の距離や密度を利用して外れ値を検出します。この手法は、データの局所的な構造を考慮できる点が特徴です。
特徴
- データポイント間の関係性を考慮
- 多次元データにも適用可能
- 非線形の関係性も捉えられる
代表的な手法
- K近傍法(K-Nearest Neighbors, KNN)
- DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
- LOF(Local Outlier Factor)
適用例
- 顧客セグメンテーション
- 画像処理における異常検出
- ネットワークトラフィック分析
時系列分析手法
時系列データは、時間の経過に伴う傾向や季節性を持つため、特別な扱いが必要です。時系列分析手法は、これらの特性を考慮して外れ値を検出します。
特徴
- 時間的な連続性を考慮
- トレンドや季節性の影響を除去可能
- 予測モデルとの組み合わせが可能
代表的な手法
- STL(Seasonal and Trend decomposition using Loess)分解
- 指数平滑法
- ARIMA(AutoRegressive Integrated Moving Average)モデル
適用例
- 株価の異常変動検出
- IoTセンサーデータの異常検知
- webトラフィックの異常検出
機械学習手法
機械学習を用いた手法は、複雑なパターンを学習し、高度な外れ値検出を行うことができます。大規模で複雑なデータセットに適しています。
特徴
- 複雑なパターンの検出が可能
- 高い精度と柔軟性
- 教師なし学習と教師あり学習の両方が適用可能
代表的な手法
- Isolation Forest
- One-Class SVM(Support Vector Machine)
- オートエンコーダー
適用例
- 不正検知
- 異常行動の検出
- 産業機器の故障予測
これらの4つのカテゴリーは、それぞれ異なる特徴と長所を持っています。実際のデータ分析では、これらの手法を単独で使用するだけでなく、複数の手法を組み合わせて使用することも多々あります。
データの性質や分析の目的、そして利用可能なリソースに応じて、適切な手法を選択することが重要です。
統計的手法:箱ひげ図とIQR法
概要
統計的手法の中でも、箱ひげ図(Box Plot)とIQR(Interquartile Range)法は、外れ値検出において非常に効果的かつ広く使用されている手法です。この方法は、データの分布を視覚化し、統計的な基準に基づいて外れ値を特定します。
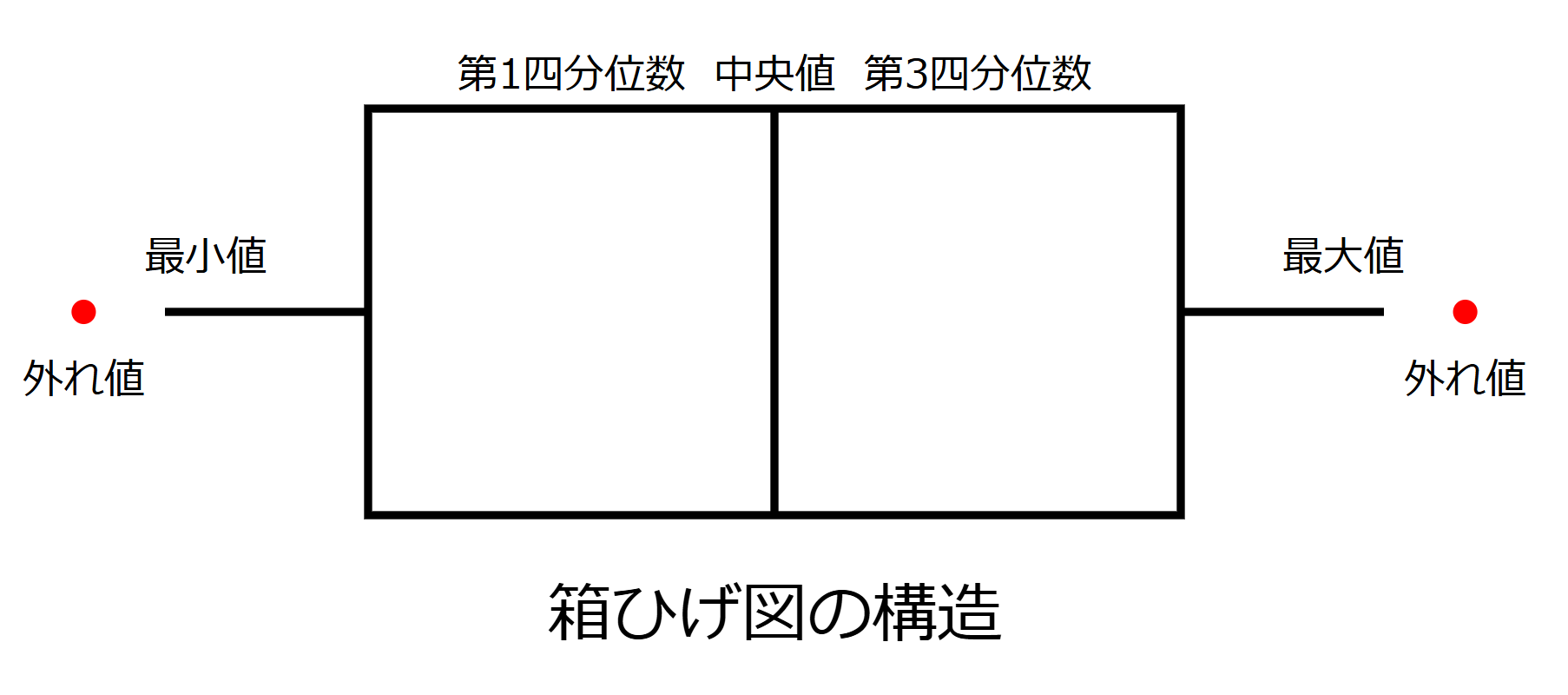
上記の図は箱ひげ図の基本構造を示しています。各要素の説明は以下の通りです。
- 箱:データの中央50%を表す。上端が第3四分位数(Q3)、下端が第1四分位数(Q1)。
- 箱の中の線:中央値(メディアン)を示す。
- ひげ:箱から伸びる線。通常のデータの範囲を示す。
- 点:外れ値を表す。ひげの外側にプロットされる。
外れ値の定義
IQR法は、箱ひげ図の構造を利用し外れ値を検知します。
Step 1 IQRの計算
- IQR = Q3 – Q1
Step 2 外れ値の定義
- 下限:Q1 – 1.5 * IQR
- 上限:Q3 + 1.5 * IQR
これらの限界を超えるデータポイントは、潜在的な外れ値として識別されます。
利点と注意点
以下、利点です。
- 視覚的理解が容易:データの分布や外れ値を一目で把握できる。
- ロバスト性:極端な値に影響されにくい。
- 計算が簡単:複雑な統計知識がなくても適用可能。
- 大規模データにも適用可能:計算効率が高い。
以下、注意点です。
- データの性質によっては過度に敏感:正規分布から大きく外れたデータでは誤検出の可能性がある。
- 単変量分析:複数の変数間の関係を考慮しない。
- コンテキストの考慮が必要:統計的に外れ値と判定されても、実際の文脈では正常な場合もある。
適用例1:異常な取引や市場動向の検出
金融分野では、箱ひげ図とIQR法を用いて、株価の変動、取引量、または取引金額などの異常を検出することができます。
例えば、日次の株価変動率の分析です。
- 過去1年間の日次株価変動率データを収集します。
- このデータに対して箱ひげ図を作成し、IQR(四分位範囲)を計算します。
- 上限値(Q3 + 1.5 * IQR)と下限値(Q1 – 1.5 * IQR)を超える変動率を異常として検出します。
このことによって、市場の通常の変動を考慮しつつ、極端な変動を客観的に特定できます。長期的なトレンドや季節性の影響を受けにくいため、真の異常を検出しやすいです。
ただし、金融市場は非常に複雑で、外部要因(例:政治的イベント、経済指標の発表)によって大きな変動が起こることがあります。そのため、検出された異常値の背景を常に調査する必要があります。
高頻度取引のデータなど、非常に大量のデータを扱う場合は、計算効率を考慮する必要があります。
適用例2:製造プロセスにおける異常値の特定
製造業では、製品の品質指標や生産ラインのパラメータを監視するために箱ひげ図とIQR法を利用できます。
例えば、自動車エンジン部品の寸法精度の管理です。
- 生産された部品のサンプルから寸法データを収集します。
- 箱ひげ図を作成し、IQRを計算して正常な寸法範囲を定義します。
- この範囲から外れる部品を異常として検出し、詳細な検査や製造プロセスの調整を行います。
このことによって、製造プロセスの安定性を視覚的に把握できます。品質管理の自動化が容易になり、人的エラーを減らすことができます。
ただし、製造プロセスに意図的な変更(例:新しい材料の導入、機械の調整)があった場合、それを考慮して基準を再設定する必要があります。
非常に厳密な許容範囲が要求される製品では、IQR法だけでなく、より厳格な管理図法(例:シューハート管理図)と組み合わせて使用することが望ましいです。
適用例3:異常気象や汚染レベルの検出
環境分野では、気温、降水量、大気汚染物質濃度などのデータに対して箱ひげ図とIQR法を適用し、異常な環境条件を検出できます。
例えば、都市の大気汚染モニタリングです。
- 複数の測定地点から日次のPM2.5濃度データを収集します。
- 各測定地点ごとに箱ひげ図を作成し、IQRを用いて正常範囲を定義します。
- この範囲を超える濃度を異常として検出し、詳細な調査や対策の必要性を判断します。
このことによって、長期的なデータから季節変動を考慮しつつ、真の異常を検出できます。複数の測定地点のデータを同時に分析し、地域間の比較が容易です。
ただし、環境データは往々にして季節性や長期的トレンドを持つため、これらの要因を考慮した分析(例:月別や季節別の箱ひげ図)が必要な場合があります。
極端な気象イベント(例:熱波、豪雨)は統計的には外れ値として検出されますが、環境変動の重要な指標である可能性があります。したがって、検出された異常値の解釈には慎重を要します。
近接性ベースの手法:K近傍法
概要
近接性ベースの手法は、データポイント間の距離や密度を利用して外れ値を検出します。その代表的な手法であるK近傍法(K-Nearest Neighbors, KNN)です。
K近傍法は、各データポイントの「近さ」を基準に外れ値を判定します。
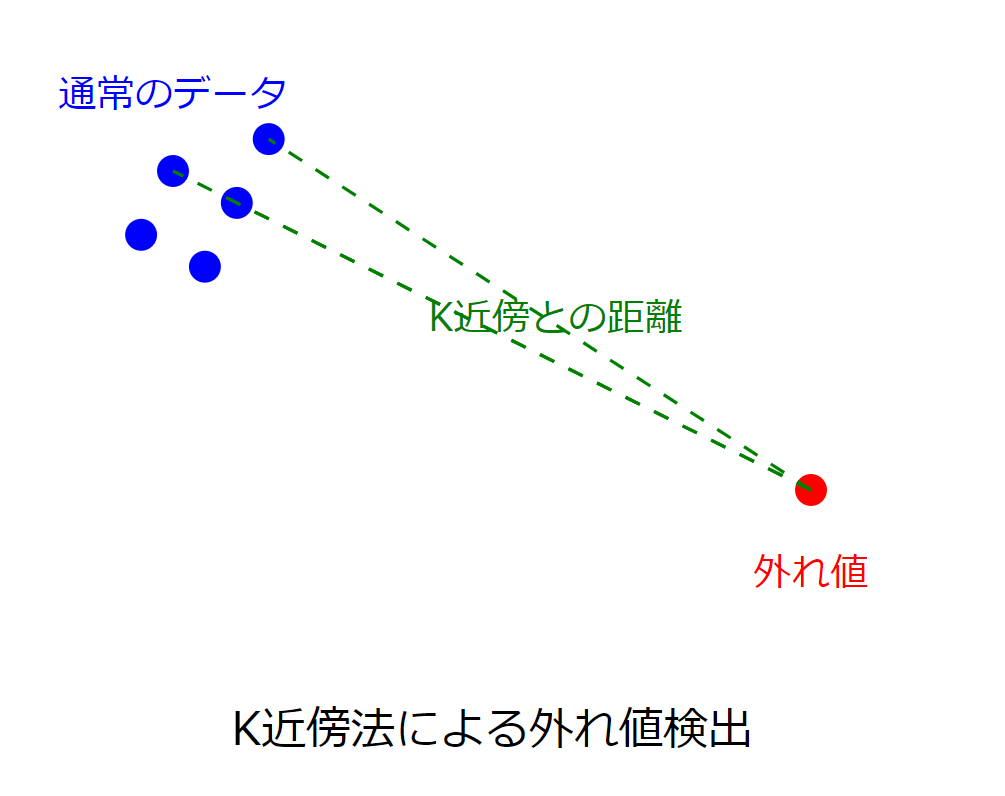
上図は、K近傍法による外れ値検出の概念を示しています。赤い点(外れ値)は他のデータポイント(青い点)から離れており、その最近傍との距離(緑の破線)が大きくなっています。
検知ステップ
Step 1 距離の計算
- ユークリッド距離やマンハッタン距離などを使用してデータポイント間の距離を計算。
Step 2 K値の選択
- データセットのサイズや次元に応じて選択(一般的には√n、nはデータ点の数)。
Step 3 近傍スコアの計算
- 各点についてK個の最近傍との平均距離や最大距離を計算。
Step 4 閾値の設定
- スコアの分布を考慮して外れ値を判定する閾値を設定。
Step 5 外れ値の判定
- スコアが閾値を超えるデータポイントを外れ値として識別。
利点と注意点
以下、利点です。
- 直感的で理解しやすい:概念が簡単で、結果の解釈が容易。
- モデルフリー:データの分布に関する事前の仮定が不要。
- 多次元データに適用可能:複数の特徴を持つデータセットにも効果的。
- 局所的な構造を考慮:データの局所的な密度を反映した判定が可能。
以下、注意点です。
- 計算コスト:大規模データセットでは計算時間が増大する可能性がある。
- K値の選択:適切なK値の選択が結果に大きく影響する。
- スケーリングの影響:特徴量のスケールが異なる場合、正規化が必要。
- 高次元データでの課題:次元の呪いにより、高次元空間では距離の概念が曖昧になる。
適用例1:不正取引の検出、リスク評価
金融分野では、K近傍法を用いて取引パターンの異常を検出し、不正取引やリスクの高い取引を特定することができます。
例えば、クレジットカード取引の不正検出です。
- 各取引を特徴量空間(例:取引金額、頻度、場所、商品カテゴリ)にマッピングします。
- 新しい取引に対して、K近傍法を適用し、最も近い既知の取引を特定します。
- 近傍の取引との類似度が低い場合、その取引を潜在的な不正としてフラグ付けし、詳細な検査する対象とします。
このことによって、複雑な取引パターンを考慮できるため、精緻な不正検出が可能です。しい不正パターンにも適応しやすく、進化する不正手法に対応できます。
ただし、適切なKの値の選択が重要で、データの特性に応じて調整が必要です。高次元データでは「次元の呪い」の影響を受ける可能性があるため、特徴量の選択や次元削減が重要です。
適用例2:異常な検査結果や症状の特定
医療分野では、K近傍法を使用して患者の検査結果や症状の異常を検出し、早期診断や治療に役立てることができます。
例えば、血液検査結果の異常検出です。
- 患者の血液検査結果(例:白血球数、赤血球数、血小板数など)を多次元空間にマッピングします。
- 新しい患者の検査結果に対してK近傍法を適用し、類似した過去の症例を特定します。
- 近傍の症例と大きく異なる結果を示す患者を、詳細な検査が必要な対象として特定します。
このことによって、複数の検査項目間の複雑な関係性を考慮した異常検出が可能です。稀少な疾患や新しい症状パターンの早期発見に役立ちます。
ただし、医療データは個人差が大きいため、年齢、性別、既往歴などの要因を考慮した分析が必要です。プライバシーとデータセキュリティの確保が極めて重要です。
適用例3:異常なネットワークトラフィックの検出
ネットワークセキュリティでは、K近傍法を使用して通常のネットワークトラフィックパターンから逸脱した異常を検出し、潜在的な脅威を特定することができます。
例えば、DDoS攻撃の検出です。
- ネットワークトラフィックデータ(例:パケット数、データ量、接続先IPアドレスの多様性)を特徴量として抽出します。
- 正常なトラフィックパターンをK近傍法でモデル化します。
- 新しいトラフィックデータに対してK近傍法を適用し、正常パターンから大きく逸脱するものを潜在的なDDoS攻撃として検出します。
このことによって、リアルタイムで大量のトラフィックデータを処理し、迅速に異常を検出できます。新しい種類の攻撃パターンにも適応しやすいです。
ただし、ネットワークトラフィックは時間帯や曜日によって大きく変動する可能性があるため、これらの要因を考慮したモデリングが必要です。
誤検知(false positives)を最小限に抑えるため、検出閾値の慎重な設定が重要です。
適用例4:製品品質の異常値検出
製造業では、K近傍法を用いて生産ラインの様々なセンサーデータから製品品質の異常を検出し、不良品の発生を未然に防ぐことができます。
例えば、半導体製造プロセスの品質管理です。
- 製造プロセスの各段階で収集されるセンサーデータ(温度、圧力、ガス流量など)を多次元空間にマッピングします。
- 良品の製造時のデータパターンをK近傍法でモデル化します。
- 新しい製造バッチのデータに対してK近傍法を適用し、通常のパターンから逸脱するものを潜在的な品質問題としてフラグ付けし、詳細な検査する対象とします。
このことによって、複数のプロセスパラメータ間の複雑な相互作用を考慮した品質管理が可能です。リアルタイムのモニタリングにより、問題の早期発見と対応が可能になります。
ただし、製造プロセスの意図的な変更(例:新しい材料の導入、設備の更新)があった場合、モデルの再学習が必要です。
製品の種類や製造条件によって正常範囲が異なる場合、それぞれに適したモデルを構築する必要があります。
時系列データにおける外れ値検出
概要
時系列データは、時間の経過に伴って収集されるデータであり、その特殊性ゆえに外れ値検出にも独自のアプローチが必要となります。
以下、時系列データの特徴により、通常の外れ値検出手法をそのまま適用すると、誤検出や見逃しが発生する可能性があります。
- 時間的依存性:データポイントが時間順に並び、互いに独立ではない。
- トレンド:長期的な上昇や下降傾向のある場合がある。
- 季節性:一定の周期で繰り返されるパターンがある場合がある。
- ノイズ:ランダムな変動がある。
時系列データの外れ値検出によく用いられる手法の一つが、STL分解です。
この方法は、時系列データを以下の3つの成分に分解します。
- 季節性(Seasonal)
- トレンド(Trend)
- 残差(Residual)
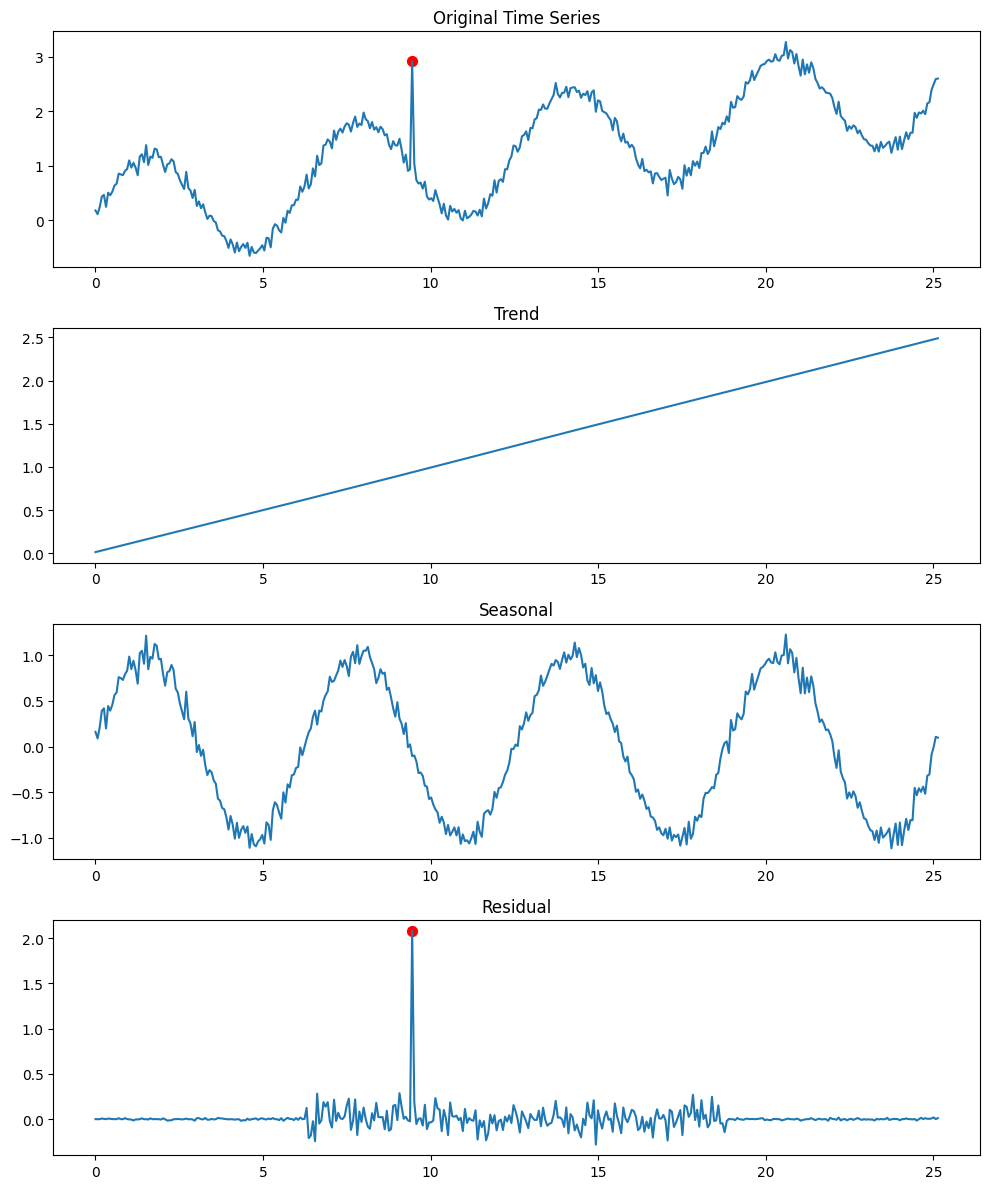
上図はSTL分解の概念を示しています。一番上の折れ線グラフが原系列、二番目がトレンド、三番目が季節性、四番目(一番下)が残差です。残差成分で外れ値(赤い点)が検出されています。
外れ値検出の手順
Step 1 データの分解
- 時系列データをSTL分解し、季節性、トレンド、残差の3成分に分ける。
Step 2 残差の分析
- 残差成分に対して、統計的手法(例:IQR法)を適用して外れ値を検出する。
Step 3 コンテキストの考慮
- 検出された外れ値を原系列と照らし合わせ、真の異常かどうかを判断する。
その他の時系列外れ値検出手法
移動平均法
- 一定期間の移動平均を計算し、それから大きく逸脱するポイントを外れ値とする。
指数平滑法
- 過去のデータに重みをつけて予測し、実際の値との差が大きいものを外れ値とする。
ARIMA(AutoRegressive Integrated Moving Average)モデル
- 時系列の自己回帰性と移動平均を考慮したモデルを構築し、予測値との差が大きいものを外れ値とする。
時系列機械学習アプローチ
- Long Short-Term Memory (LSTM) ネットワークなどの深層学習モデルを使用して、異常を検出する。
利点と注意点
以下、利点です。
- 時間的文脈の考慮:データの時間的な特性を反映した検出が可能。
- トレンドと季節性の分離:長期的傾向や周期的パターンの影響を除去できる。
- 動的な閾値:データの変化に応じて柔軟に閾値を調整できる。
以下、注意点です。
- パラメータ設定の重要性:STL分解やARIMAモデルのパラメータ選択が結果に大きく影響する。
- 計算コスト:複雑なモデルでは計算時間が増大する可能性がある。
- 非定常性への対応:強い非定常性を持つデータでは、追加の前処理が必要な場合がある。
適用例1:株価や為替レートの急激な変動の特定
経済指標の分析では、時系列データの特性を考慮しつつ、急激な変動を検出することが重要です。
例えば、日次の為替レート変動の異常検出です。
- 過去数年分の日次為替レートデータを収集します。
- STL(Seasonal and Trend decomposition using Loess)分解を適用し、データをトレンド、季節性、残差成分に分解します。
- 残差成分に対して、移動平均と移動標準偏差を計算し、信頼区間を設定します。
- この信頼区間を超える変動を異常として検出します。
このことによって、長期的なトレンドや季節性の影響を除去した上で、真の異常を検出できます。市場の通常の変動性を考慮しつつ、異常な変動を特定できます。
ただし、経済指標は外部イベント(政策変更、地政学的リスクなど)に敏感であるため、検出された異常の背景を常に調査する必要があります。
金融市場の変動性自体が時間とともに変化する可能性があるため、モデルの定期的な再評価と調整が必要です。
適用例2:機器の異常動作や故障の早期発見
IoTデバイスから収集される大量の時系列データを分析し、機器の異常を早期に発見することができます。
例えば、工場の生産設備のセンサーデータ分析です。
- 設備から継続的に収集される温度、振動、電力消費などのデータを時系列として扱います。
- 各センサーデータに対してSTL分解を適用し、トレンドと季節性を除去します。
- 残差成分に対して、動的閾値(例:指数移動平均法を用いた予測区間)を設定します。
- この閾値を超えるデータポイントを異常として検出し、潜在的な故障や異常動作を早期に特定します。
このことによって、機器の通常の動作パターン(例:稼働時間による温度変化)を考慮しつつ、真の異常を検出できます。リアルタイムでの監視が可能で、問題の早期発見と対応が可能になります。
ただし、機器のメンテナンスや設定変更などの計画的な変更を考慮に入れる必要があります。複数のセンサー間の相関関係も考慮することで、より精度の高い異常検出が可能になります。
適用例3:サイトへの異常アクセスやDDoS攻撃の検出
Webサイトのトラフィックデータは典型的な時系列データであり、その分析によって異常なアクセスパターンを検出できます。
例えば、Webサーバーのアクセスログ分析です。
- サーバーのアクセスログから、時間単位のリクエスト数、ユニークIPアドレス数などの時系列データを作成します。
- これらのデータに対してSTL分解を適用し、通常の日内変動やトレンドを分離します。
- 残差成分に対して、統計的管理図(例:CUSUM管理図)を適用し、異常を検出します。
- 急激なリクエスト数の増加や通常とは異なるアクセスパターンを示すデータポイントを、潜在的なDDoS攻撃や異常アクセスとしてフラグ付けし、詳細な検査する対象とします。
このことによって、サイトの通常のトラフィックパターン(例:業務時間中の増加、週末の減少)を考慮しつつ、異常を検出できます。リアルタイムでの監視が可能で、攻撃の早期検出と対応が可能になります。
ただし、正当な大規模イベント(例:大規模セールの開始、人気コンテンツの公開)による一時的なトラフィック増加を、誤って攻撃と判断しないよう注意が必要です。
トラフィックパターンは時間とともに進化する可能性があるため、モデルの定期的な再学習が必要です。
適用例4:異常気象や気候変動の兆候の特定
長期的な気象データの分析により、異常気象イベントの検出や気候変動の兆候を特定することができます。
例えば、日平均気温データの長期分析です。
- 数十年分の日平均気温データを収集します。
- STL分解を適用して、長期的なトレンド、季節変動、および残差成分に分解します。
- トレンド成分の変化率を分析し、気候変動の兆候を特定します。
- 残差成分に対して、外れ値検出手法(例:修正されたZ-スコア法)を適用し、異常気象イベントを検出します。
このことによって、季節変動や長期的なトレンドを考慮しつつ、真の異常気象イベントを特定できます。気候変動の長期的な兆候を定量的に分析することができます。
ただし、気象データは地理的な要因に大きく影響されるため、地域ごとの分析が必要です。気候変動自体が「新しい正常」を生み出す可能性があるため、「異常」の定義を定期的に見直す必要があります。
極端な気象イベントは統計的には外れ値として検出されますが、気候変動の重要な指標である可能性があるため、慎重な解釈が必要です。
機械学習を用いた外れ値検出:Isolation Forest
概要
機械学習アルゴリズムは、複雑なパターンを学習し、高度な外れ値検出を可能にします。
Isolation Forestは、外れ値が「他のデータポイントから孤立している」という特性を利用します。
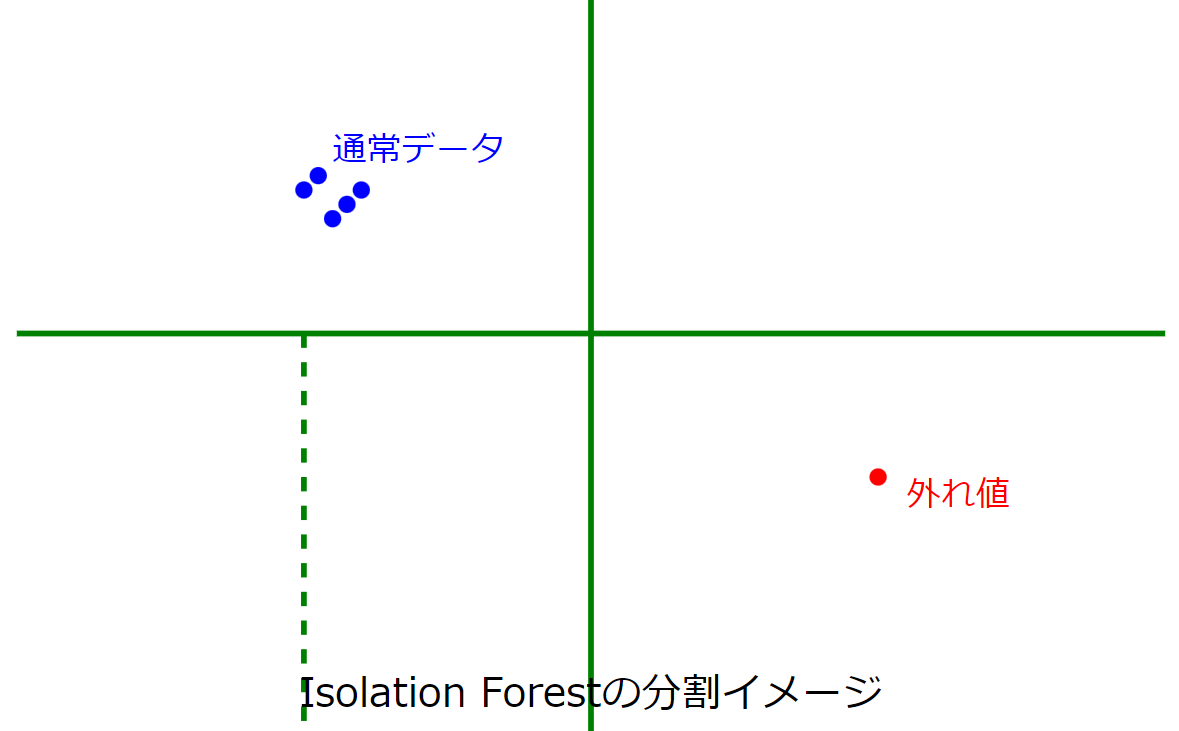
上図は、Isolation Forestの基本的な考え方を示しています。通常のデータ(青い点)は密集しているため、多くの分割(緑の線)が必要ですが、外れ値(赤い点)は少ない分割で孤立します。
外れ値検知アルゴリズム
Step 1 サブサンプリング
- データセットからランダムにサブサンプルを抽出。
Step 2 iTreeの構築
- 各サブサンプルに対して、ランダムな特徴と分割点を選択。
- データポイントが1つになるまで、または最大深さに達するまで再帰的に分割。
Step 3 アノマリースコアの計算
- 各データポイントについて、複数のiTreeでの平均パス長を計算。
- パス長が短いほど、そのデータポイントは外れ値である可能性が高い。
Step 4 外れ値の判定
- スコアに基づいて閾値を設定し、外れ値を判定。
利点と注意点
以下、利点です。
- 高い効率性:計算量がO(n log n)と比較的低く、大規模データセットにも適用可能。
- 次元の呪いに強い:高次元データでも効果的に機能する。
- モデルフリー:データの分布に関する事前の仮定が不要。
- 解釈可能性:各特徴の重要度を評価できる。
以下、注意点です。
- ランダム性の影響:結果が実行ごとに若干異なる可能性がある。
- 密度ベースの異常に弱い:非常に密集したクラスター内の異常を見逃す可能性がある。
- パラメータ調整:サブサンプルサイズや木の数などのパラメータ調整が必要。
適用例1:異常なネットワークトラフィックや不正アクセスの検出
サイバーセキュリティ分野では、Isolation Forestを用いて大量のネットワークトラフィックデータから異常を効率的に検出することができます。
例えば、ネットワーク侵入検知システム(IDS)の強化です。
- ネットワークパケットから特徴量を抽出します(例:送信元/送信先IPアドレス、ポート番号、プロトコル、パケットサイズ、接続持続時間など)。
- これらの特徴量を用いてIsolation Forestモデルを学習させます。
- リアルタイムで新しいネットワークトラフィックデータに対してモデルを適用し、異常スコアを計算します。
- 高い異常スコアを持つトラフィックを潜在的な脅威としてフラグ付けし、詳細な調査を行います。
このことによって、高次元データを効率的に処理できるため、多様な特徴量を考慮した分析が可能です。
新しい種類の攻撃パターンに対しても効果的に機能する可能性があります。計算効率が良いため、大量のリアルタイムデータ処理に適しています。
ただし、正常なトラフィックパターンが時間とともに変化する可能性があるため、モデルの定期的な再学習が必要です。
誤検知を減らすため、検出された異常に対する人間の専門家による検証プロセスを組み込むことが重要です。
適用例2:不正取引の検出、リスク評価
金融分野では、Isolation Forestを使用して大量の取引データから不正や高リスクの取引を効率的に検出することができます。
例えば、クレジットカード取引の不正検出システムです。
- 各取引から多数の特徴量を抽出します(例:取引額、時間、場所、商品カテゴリ、過去の取引パターンなど)。
- これらの特徴量を用いてIsolation Forestモデルを学習させます。
- 新しい取引が発生するたびに、モデルを適用して異常スコアを計算します。
- 高い異常スコアを持つ取引を潜在的な不正としてフラグ付けし、追加の認証や調査を行います。
このことによって、多様な特徴量を考慮できるため、複雑な不正パターンの検出が可能です。
モデルの学習と予測が高速であるため、リアルタイムでの不正検出に適しています。新しい種類の不正パターンに対しても一定の効果を発揮する可能性があります。
ただし、正常な取引パターンが季節性や特別なイベントにより変化する可能性があるため、これらの要因を考慮したモデリングが必要です。
誤って正常な取引を不正と判断することによる顧客体験の低下を防ぐため、適切な閾値設定が重要です。
適用例3:製品品質の異常値検出、設備の故障予測
製造業では、Isolation Forestを用いて生産ラインの多様なセンサーデータから品質異常や設備故障の予兆を検出することができます。
例えば、半導体製造プロセスの品質管理と設備故障予測です。
- 製造プロセスの各段階で収集される多数のセンサーデータ(温度、圧力、ガス流量、電流値など)を特徴量として使用します。
- これらの特徴量を用いてIsolation Forestモデルを学習させます。
- 新しい製造バッチのデータに対してリアルタイムでモデルを適用し、異常スコアを計算します。
- 高い異常スコアを示すデータポイントを、潜在的な品質問題や設備故障の予兆としてフラグ付けし、詳細な検査の対象とします。
このことによって、多数のセンサーデータを同時に考慮できるため、複雑な相互作用を持つ異常を検出できます。
計算効率が良いため、リアルタイムのモニタリングが可能です。新しい種類の異常パターンに対しても一定の検出能力を持つ可能性があります。
ただし、製造プロセスの意図的な変更(新しい製品ライン、設備のアップグレードなど)があった場合、モデルの再学習が必要です。
検出された異常の原因特定のため、機械学習の専門家と製造プロセスの専門家の協力が重要です。
適用例4:画像診断における異常な所見の検出、稀少な症例の特定
医療分野では、Isolation Forestを画像診断や症例データの分析に適用し、異常な所見や稀少な症例を効率的に検出することができます。
例えば、MRI画像からの異常所見の自動検出です。
- MRI画像から多数の特徴量を抽出します(例:テクスチャ特徴、形状特徴、位置情報など)。
- 正常な画像データを用いてIsolation Forestモデルを学習させます。
- 新しいMRI画像に対してモデルを適用し、異常スコアを計算します。
- 高い異常スコアを示す画像や画像の特定部分を、詳細な検査が必要な潜在的な異常としてフラグ付けします。
このことによって、高次元の画像データを効率的に処理できるため、多様な特徴を考慮した分析が可能です。
稀少な異常パターンの検出に優れているため、珍しい疾患の早期発見に役立つ可能性があります。教師なし学習アプローチのため、ラベル付きデータが少ない稀少疾患の検出にも適用できます。
ただし、医療画像の複雑性を考慮し、適切な特徴抽出方法の選択が重要です。
検出された異常の臨床的意義を判断するため、医療専門家による検証が不可欠です。患者のプライバシーとデータセキュリティの確保には特に注意が必要です。
今回のまとめ
今回は、データ分析における重要なテーマである外れ値検出について、基本的な概念から高度な手法まで幅広く解説しました。
外れ値は単なるノイズではなく、重要な洞察や異常を示す可能性があります。適切に検出し解釈することで、ビジネスや研究に大きな価値をもたらします。
外れ値は、単一の手法に頼るのではなく、複数の手法を組み合わせることで、より信頼性の高い結果が得られます。
- 統計的手法(箱ひげ図、IQR法):データの分布に基づく伝統的なアプローチ
- 近接性ベース手法(K近傍法):データポイント間の距離や密度を利用
- 時系列分析(STL分解):時間的特性を考慮した手法
- 機械学習アプローチ(Isolation Forest):複雑なパターンを学習し、高度な検出を実現
そして、単にアルゴリズムにだけに頼るのではなく、データの性質やドメイン知識を考慮し、検出された外れ値の意味を適切に解釈することが重要です。
外れ値検出は、データ分析の重要な要素であり、適切に実施することで隠れた問題や機会を発見できます。紹介した手法とアプローチを基に、皆さんのデータ分析プロジェクトでより深い洞察を得られることを願っています。
最後に、外れ値検出はツールであり、目的ではありません。検出された外れ値に対して適切なアクションを取ることで、初めて真の価値が生まれます。
常に批判的思考を保ち、検出結果の意味を深く考察することを忘れないでください。

