A/Bテストは、マーケティングや製品開発において重要な手法の一つです。
異なる施策を比較し、その効果を評価するために使用されます。
しかし、A/Bテストを正確に実施するためには、適切な統計検定を選ぶことが不可欠です。
今回は、どのような条件下でどの統計検定を使用すべきかをフローチャートを使って解説します。
Contents [hide]
- A/Bテストの基本的な概念
- A/Bテストとは
- A/Bテストの目的
- A/Bテストの一般的なプロセス
- 統計検定の選択ガイド
- 問1)計測対象はカテゴリカル(質的)ですか?
- 問2-1)[カテゴリカル(質的)] サンプルサイズは大きいですか?
- 問2-2)[ニューメリカル(量的)] サンプルサイズは小さいですか?
- 問3)正規分布ではないですか?
- 問4)分散が既知ですか?
- 問5) 分散が類似していますか?
- 各統計検定手法
- Pearsonのカイ二乗検定
- Fisherの正確確率検定
- Z検定
- Studentのt検定
- Welchのt検定
- Mann-WhitneyのU検定
- A/Bテストの最適化方法
- Step 1 明確な目標設定
- Step 2 適切なサンプルサイズの計算
- Step 3 テストの期間を適切に設定
- Step 4 複数の指標をモニタリング
- Step 5 継続的なテストと改善
- Step 6 高度なテスト手法の活用
- Step 7 ツールの活用
- 今回のまとめ
A/Bテストの基本的な概念
A/Bテストとは
A/Bテストは、二つの異なるバージョン(AとB)の施策を比較し、その効果を評価するための実験手法です。
例えば、新しいウェブサイトのデザインや広告のコピー、プロモーションの内容などをテストし、どちらがより良い結果をもたらすかを確認するために使用されます。
A/Bテストの目的
A/Bテストの主な目的は、エビデンスに基づいた意思決定を行うことです。
直感や経験だけでなく、データに基づいて最適な施策を選択することで、ビジネスの成果を最大化することができます。
A/Bテストは、マーケティング、ユーザーエクスペリエンスの改善、プロダクト開発など、さまざまな分野で活用されています。
A/Bテストの一般的なプロセス
A/Bテストを実施する際の一般的なプロセスは以下の通りです。
Step 1 目的の設定
- テストの目的を明確にする。
- 例えば、「新しいデザインがコンバージョン率を改善するかどうかを確認する」といった具体的な目的を設定します。
Step 2 仮説の立案
- テストする施策(AとB)についての仮説を立てます。
- 例えば、「新しいデザインBは、現行のデザインAよりもコンバージョン率が高い」と仮定します。
Step 3 サンプルの選定
- テスト対象となるユーザーグループをランダムに分け、グループAとグループBに割り当てます。
- これにより、バイアスを排除し、公平な比較が可能になります。
Step 4 テストの実施
- 両グループに対して異なるバージョンの施策を提示し、一定期間データを収集します。
Step 4 データの分析
- テスト終了後、収集したデータを統計的に分析し、仮説が正しいかどうかを検証します。
- このステップで適切な統計検定を選ぶことが重要です。
Step 5 結果の解釈と結論
- 分析結果に基づき、どちらの施策がより効果的かを判断します。
- そして、その結果を基に意思決定を行い、実際の施策に反映します。
A/Bテストは、データに基づいた意思決定を支援するための強力なツールです。
基本的なプロセスを理解し、適切に実施することで、ビジネスの成果を向上させることができます。
統計検定の選択ガイド
A/Bテストにおいて、適切な統計検定を選ぶことは、テスト結果の信頼性を確保するために非常に重要です。
統計検定は、データの性質や条件に基づいて選択されるべきです。
フローチャートを使用して統計検定の選択ガイドを説明します。
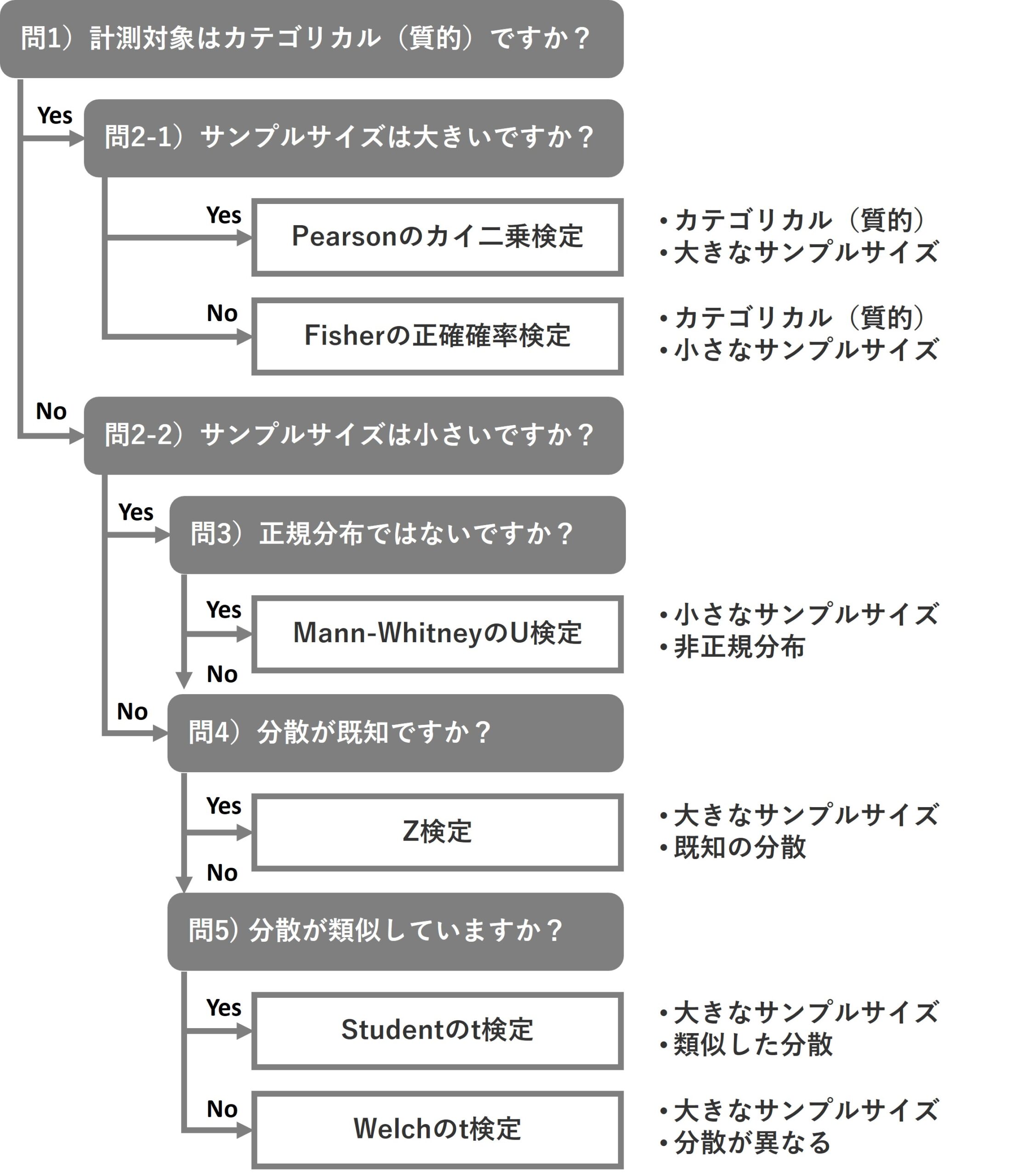
問1)計測対象はカテゴリカル(質的)ですか?
まず、計測する変数はカテゴリカル(質的)かどうかを確認します。例えば、クリックの有無や購入の有無などがあります。
- Yes(はい): 問2-1)に進みます。
- No(いいえ): そうでない場合は、問2-2)に進みます。
問2-1)[カテゴリカル(質的)] サンプルサイズは大きいですか?
サンプルサイズが十分に大きいかどうかを確認します。一般的に、各グループで30以上のサンプルがあれば「大きい」とされます。
- Yes(はい): サンプルサイズが大きい場合は、Pearsonのカイ二乗検定を使用します。
- No(いいえ): そうでない場合は、Fisherの正確確率検定を使用します。
問2-2)[ニューメリカル(量的)] サンプルサイズは小さいですか?
サンプルサイズが十分に大きいかどうかを確認します。一般的に、各グループで30以上のサンプルがあれば「大きい」とされます。
- Yes(はい): サンプルサイズが小さい場合は、問3)に進みます。
- No(いいえ): そうでない場合は、問4)に進みます。
問3)正規分布ではないですか?
正規分布と見なせるかどうかを確認します。
- Yes(はい): 正規分布と見なせない場合は、Mann-WhitneyのU検定を使用します。
- No(いいえ): そうでない場合(正規分布と見なせる場合)は、問4)に進みます。
問4)分散が既知ですか?
両グループのデータの分散が既知かどうかを確認します。これは、事前に分散が分かっている場合や、過去のデータから推測できる場合に適用されます。
- Yes(はい): 分散が分かっている場合は、Z検定を使用します。
- No(いいえ): そうでない場合は、問5)に進みます。
問5) 分散が類似していますか?
両グループのデータの分散が類似しているかどうかを確認します。分散が類似している場合、より一般的なt検定が使用されます。
- Yes(はい): 分散が類似している場合は、Studentのt検定を使用します。
- No(いいえ): そうでない場合は、Welchのt検定を使用します。
各統計検定手法

基本的な統計検定手法を簡単に説明します。
Pearsonのカイ二乗検定
Pearsonのカイ二乗検定は、カテゴリーデータの独立性を検定する方法です。
- 帰無仮説 (H0): 二つのカテゴリ変数は独立している。
- 対立仮説 (H1): 二つのカテゴリ変数は独立していない。
例えば、広告のクリック率が異なるバージョン間で独立しているかどうかを確認するために使用されます。
例として、ウェブサイトのA/Bテストで、広告のクリック率を比較します。
データ
- Aグループ: クリック数 = 300, 非クリック数 = 700
- Bグループ: クリック数 = 350, 非クリック数 = 650
結果の解釈
- p値が0.05未満の場合、広告のクリック率に有意な差があると結論付けます。
Fisherの正確確率検定
Fisherの正確確率検定は、小さなサンプルサイズでのカテゴリーデータの独立性を検定する方法です。クロス集計表の各セルに小さな値が含まれている場合に適しています。
- 帰無仮説 (H0): 二つのカテゴリ変数は独立している。
- 対立仮説 (H1): 二つのカテゴリ変数は独立していない。
少数のサンプルによる広告のクリック率を比較します。
データ
- Aグループ: クリック数 = 10, 非クリック数 = 30
- Bグループ: クリック数 = 15, 非クリック数 = 25
結果の解釈
- p値が0.05未満の場合、広告のクリック率に有意な差があると結論付けます。
Z検定
Z検定は、二つの独立したサンプルの平均値の差を検定する方法です。分散が既知の場合に適しています。
- 帰無仮説 (H0): 二つのサンプルの平均値に差はない。
- 対立仮説 (H1): 二つのサンプルの平均値に差がある。
平均売上を比較します。
データ
- Aグループ: 平均売上 = 200, 標準偏差 = 50, サンプル数 = 100
- Bグループ: 平均売上 = 210, 標準偏差 = 50, サンプル数 = 100
結果の解釈
- p値が0.05未満の場合、平均売上に有意な差があると結論付けます。
Studentのt検定
Studentのt検定は、二つの独立したサンプルの平均値の差を検定する方法です。分散が類似している場合に適しています。
- 帰無仮説 (H0): 二つのサンプルの平均値に差はない。
- 対立仮説 (H1): 二つのサンプルの平均値に差がある。
サンプル間の平均値を比較します。
データ
- Aグループ: 平均 = 50, 標準偏差 = 10, サンプル数 = 30
- Bグループ: 平均 = 55, 標準偏差 = 10, サンプル数 = 30
結果の解釈
- p値が0.05未満の場合、平均値に有意な差があると結論付けます。
Welchのt検定
Welchのt検定は、二つの独立したサンプルの平均値の差を検定する方法です。分散が異なる場合に適しています。
- 帰無仮説 (H0): 二つのサンプルの平均値に差はない。
- 対立仮説 (H1): 二つのサンプルの平均値に差がある。
異なる条件下での平均収入を比較します。
データ
- Aグループ: 平均 = 50, 標準偏差 = 15, サンプル数 = 30
- Bグループ: 平均 = 55, 標準偏差 = 20, サンプル数 = 30
結果の解釈
- p値が0.05未満の場合、平均収入に有意な差があると結論付けます。
Mann-WhitneyのU検定
Mann-WhitneyのU検定は、二つの独立したサンプルの順位データを比較する非パラメトリック検定です。サンプルサイズが小さく、正規分布に従わない場合に適しています。
- 帰無仮説 (H0): 二つのサンプルの中央値に差はない。
- 対立仮説 (H1): 二つのサンプルの中央値に差がある。
ランキングデータの比較を行います。
データ
- Aグループ: [1, 3, 5, 7, 9]
- Bグループ: [2, 4, 6, 8, 10]
結果の解釈
- p値が0.05未満の場合、ランキングデータに有意な差があると結論付けます。
A/Bテストの最適化方法

A/Bテストの基本を理解し、実施することができるようになったら、次はそのプロセスを最適化することで、より効果的で効率的なテストを実現できます。
明確な目標設定から始まり、適切なサンプルサイズの計算、テスト期間の設定、複数の指標のモニタリング、継続的な改善、高度なテスト手法の活用、そして適切なツールの使用を含みます。
これらの方法を駆使することで、テストの精度と効率を向上させ、より確実な意思決定をサポートすることができます。
Step 1 明確な目標設定
A/Bテストを実施する前に、明確な目標を設定することが重要です。
テストの目的が明確であればあるほど、適切な指標を選び、結果を正確に評価することができます。
たとえば……
- コンバージョン率の向上
- 平均注文額の増加
- ユーザーエンゲージメントの向上
Step 2 適切なサンプルサイズの計算
サンプルサイズが小さすぎると、結果が統計的に有意でにくい可能性があり、大きすぎるとリソースの無駄になります。
適切なサンプルサイズを計算することで、効率的なテストを実現できます。
例えば、パワーアナリシスを使用して、必要なサンプルサイズを計算します。
これは、期待される効果の大きさ(エフェクトサイズ)と望む信頼水準(通常95%)を基に計算されます。
Step 3 テストの期間を適切に設定
テスト期間が短すぎると、データが不十分であり、長すぎると環境の変化が影響を与える可能性があります。
適切な期間を設定し、テストを実施することが重要です。
例えば、テスト期間は少なくとも1~2週間とし、曜日や時間帯の影響を考慮します。
Step 4 複数の指標をモニタリング
主要な指標だけでなく、関連するサブ指標もモニタリングすることで、テストの影響を総合的に評価できます。
これにより、予期しない影響を早期に発見することができます。
例えば、コンバージョン率だけでなく、バウンス率やページビュー数もモニタリングする。
Step 5 継続的なテストと改善
A/Bテストは一度実施して終わりではなく、継続的に実施し、改善を続けることが重要です。
常に新しい仮説を立て、テストを繰り返すことで、最適な結果を追求します。
例えば、テスト結果に基づいて新たな仮説を立て、次のテストを計画します。
Step 6 高度なテスト手法の活用
基本的なA/Bテストに加え、以下のような高度なテスト手法を活用することで、より精緻な分析が可能になります。
- 多変量テスト(MVT): 複数の要素を同時にテストし、それぞれの要素がどのように影響するかを分析します。
- ベイジアンA/Bテスト: ベイジアン統計を用いたテスト手法で、結果の不確実性を考慮しながらテストを進めます。
- セグメント別分析: ユーザーセグメントごとにテスト結果を分析し、特定のユーザーグループに対する効果を評価します。
Step 7 ツールの活用
A/Bテストを効率的に実施するために、専門的なツールを活用することも重要です。
例えば、次のようなツールがあります。
- Google Optimize: 無料で使用できるA/Bテストツール。
- Optimizely: 高機能なA/Bテストと多変量テストのツール。
今回のまとめ
今回は、「A/Bテストをするとき、どの統計検定を使うべきか?」というテーマで、A/Bテストの基本概念から適切な統計検定の選び方を簡易的に説明しました。
A/Bテストの重要性について説明しました。A/Bテストは異なる施策を比較して効果を評価するための重要な手法であり、データに基づいた意思決定を行うために欠かせないものです。
適切な統計検定を選ぶことの重要性に触れました。正しい検定を選ぶことで、テスト結果の信頼性が向上し、より確実な結論を導き出すことができます。
どの統計検定を選ぶべきかを、フローチャートを使って具体的な条件に基づいた統計検定の選び方をガイドし、各検定につてい示しました。
A/Bテストを成功させるためには、適切な検定を選び、テスト結果の信頼性を高めることで、データに基づいた意思決定が可能となり、ビジネスの成果を向上させることができます。