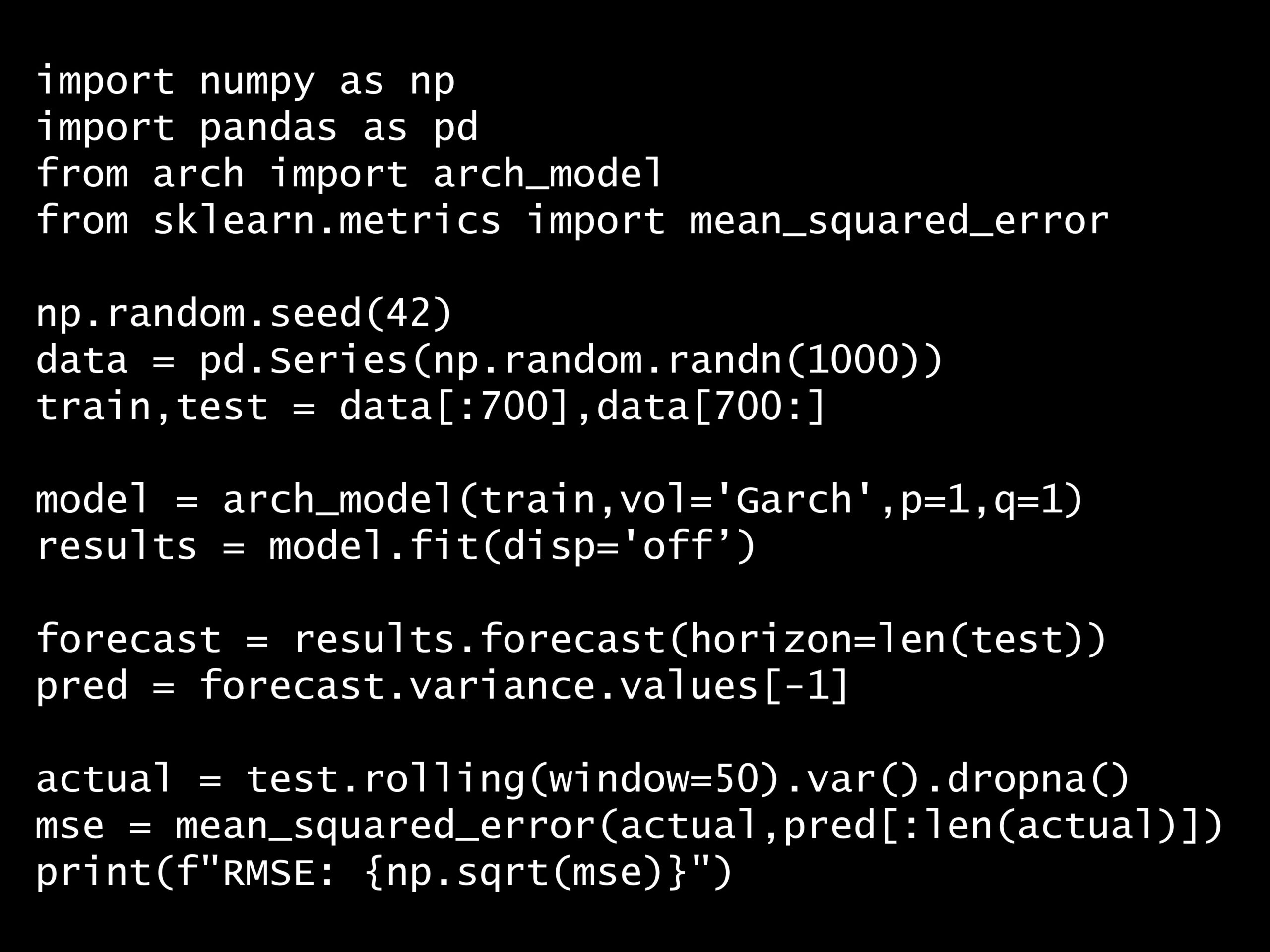
Python 時系列分析 1,000本ノック– ノック65: 時系列の分散予測精度評価 –

問題
答え
解説

次の Python コードは、どの評価方法を実施していますか？

Python コード:

import numpy as np

import pandas as pd

from arch import arch_model

from sklearn.metrics import mean_squared_error

np.random.seed(42)

data = pd.Series(np.random.randn(1000))

train,test = data[:700],data[700:]

model = arch_model(train,vol='Garch',p=1,q=1)

results = model.fit(disp='off')

forecast = results.forecast(horizon=len(test))

pred = forecast.variance.values[-1]

actual = test.rolling(window=50).var().dropna()

mse = mean_squared_error(actual,pred[:len(actual)])

print(f"RMSE: {np.sqrt(mse)}")

import numpy as np import pandas as pd from arch import arch_model from sklearn.metrics import mean_squared_error np.random.seed(42) data = pd.Series(np.random.randn(1000)) train,test = data[:700],data[700:] model = arch_model(train,vol='Garch',p=1,q=1) results = model.fit(disp='off') forecast = results.forecast(horizon=len(test)) pred = forecast.variance.values[-1] actual = test.rolling(window=50).var().dropna() mse = mean_squared_error(actual,pred[:len(actual)]) print(f"RMSE: {np.sqrt(mse)}")

import numpy as np
import pandas as pd
from arch import arch_model
from sklearn.metrics import mean_squared_error

np.random.seed(42)
data = pd.Series(np.random.randn(1000))
train,test = data[:700],data[700:]

model = arch_model(train,vol='Garch',p=1,q=1)
results = model.fit(disp='off')

forecast = results.forecast(horizon=len(test))
pred = forecast.variance.values[-1]

actual = test.rolling(window=50).var().dropna()

mse = mean_squared_error(actual,pred[:len(actual)])
print(f"RMSE: {np.sqrt(mse)}")

回答の選択肢:

(A) ヒットレート
(B) 逆分散比率検定
(C) バックテスト
(D) 交差検証

出力例:

RMSE: 0.17436399336238564

正解: (C)
回答の選択肢:

(A) ヒットレート
(B) 逆分散比率検定
(C) バックテスト
(D) 交差検証

コードの解説

このコードは、時系列データの分散予測精度を評価するためのものです。

import numpy as np

import pandas as pd

from arch import arch_model

from sklearn.metrics import mean_squared_error

np.random.seed(42)

data = pd.Series(np.random.randn(1000))

train,test = data[:700],data[700:]

model = arch_model(train,vol='Garch',p=1,q=1)

results = model.fit(disp='off')

forecast = results.forecast(horizon=len(test))

pred = forecast.variance.values[-1]

actual = test.rolling(window=50).var().dropna()

mse = mean_squared_error(actual,pred[:len(actual)])

print(f"RMSE: {np.sqrt(mse)}")

import numpy as np
import pandas as pd
from arch import arch_model
from sklearn.metrics import mean_squared_error

np.random.seed(42)
data = pd.Series(np.random.randn(1000))
train,test = data[:700],data[700:]

model = arch_model(train,vol='Garch',p=1,q=1)
results = model.fit(disp='off')

forecast = results.forecast(horizon=len(test))
pred = forecast.variance.values[-1]

actual = test.rolling(window=50).var().dropna()

mse = mean_squared_error(actual,pred[:len(actual)])
print(f"RMSE: {np.sqrt(mse)}")

詳しく説明します。

1000個の標準正規分布に従う乱数データを生成します。

np.random.seed(42)

data = pd.Series(np.random.randn(1000))

np.random.seed(42) data = pd.Series(np.random.randn(1000))

np.random.seed(42)
data = pd.Series(np.random.randn(1000))

データを訓練データ（最初の700個）とテストデータ（最後の300個）に分割します。

train,test = data[:700],data[700:]

train,test = data[:700],data[700:]

訓練データに対してGARCH(1,1)モデルを定義し、フィッティングします。

model = arch_model(train,vol='Garch',p=1,q=1)

results = model.fit(disp='off')

model = arch_model(train,vol='Garch',p=1,q=1) results = model.fit(disp='off')

model = arch_model(train,vol='Garch',p=1,q=1)
results = model.fit(disp='off')

テストデータの長さに基づいて分散の予測を行います。

forecast = results.forecast(horizon=len(test))

pred = forecast.variance.values[-1]

forecast = results.forecast(horizon=len(test)) pred = forecast.variance.values[-1]

forecast = results.forecast(horizon=len(test))
pred = forecast.variance.values[-1]

実際の分散を計算するために、テストデータに対して50期間の移動分散を計算します。

actual = test.rolling(window=50).var().dropna()

actual = test.rolling(window=50).var().dropna()

予測された分散と実際の分散を比較し、平均二乗誤差（MSE）を計算します。

mse = mean_squared_error(actual,pred[:len(actual)])

mse = mean_squared_error(actual,pred[:len(actual)])

MSEの平方根（RMSE）を出力します。

print(f"RMSE: {np.sqrt(mse)}")

print(f"RMSE: {np.sqrt(mse)}")

RMSE: 0.17436399336238564

GARCHモデルとは？

GARCHモデル（Generalized Autoregressive Conditional Heteroskedasticityモデル）について説明します。

GARCHモデルは、時系列データの分散（ボラティリティ）が時間とともに変動することを捉えるための統計的手法です。特に金融データにおいて、価格の変動性を予測するために広く使用されます。

GARCHモデルは、ARCHモデル（Autoregressive Conditional Heteroskedasticityモデル）を一般化したもので、過去の分散も考慮に入れることで、より柔軟なモデル化が可能です。

GARCHモデルの基本的なアイデアは、現在の分散が過去の誤差項と過去の分散の線形結合で表されるというものです。具体的には、GARCH(p, q)モデルでは、pは過去の分散のラグ数、qは過去の誤差項のラグ数を示します。

GARCH(1,1)モデルの数式は以下の通りです。

平均方程式

\displaystyle y_t = \mu + \epsilon_t

ここで、 $y_t$ は時系列データ、 $\mu$ は定数、 $\epsilon_t$ は誤差項です。

分散方程式

\displaystyle \sigma_t^2 = \alpha_0 + \alpha_1 \epsilon_{t-1}^2 + \beta_1 \sigma_{t-1}^2

ここで、 $\sigma_t^2$ は時点tにおける分散、 $\alpha_0$ 、 $\alpha_1$ 、 $\beta_1$ はモデルのパラメータです。

GARCHモデルの利点は、金融市場の価格変動やリスク管理、ポートフォリオの最適化などにおいて重要な役割を果たすことです。

ボラティリティモデルを使用することで、将来の価格変動の予測やリスク評価が可能となり、投資戦略の策定やリスク管理に役立ちます。

分散の予測精度評価方法

GARCHモデルの分散予測精度を評価するための方法には、以下のようなものがあります。

バックテスト

過去のデータを使用してモデルを訓練し、その後、未知のデータに対して予測を行い、実際の結果と比較する手法です。
予測された分散と実際の分散を比較することで、モデルの予測精度を評価します。

ヒットレート

予測された分散が実際の分散をどれだけ正確に捉えているかを評価する方法です。
具体的には、予測された分散が実際の分散の範囲内に収まる割合を計算します。

逆分散比率検定

予測された分散と実際の分散の比率を計算し、その逆数を取ることで、予測精度を評価します。
この方法は、予測された分散が実際の分散に対してどれだけ過大または過小評価されているかを示します。

交差検証

データを複数の部分に分割し、各部分をテストデータとして使用し、残りの部分を訓練データとして使用する方法です。
これにより、モデルの予GARCHモデルの分散予測精度を評価するための方法には、以下のようなものがあります：

これらの方法を組み合わせて使用することで、GARCHモデルの分散予測精度を総合的に評価することができます。

Pythonの実装例

Contents [hide]

バックテスト
ヒットレート
逆分散比率検定
交差検証

バックテスト

過去のデータを使用してモデルを訓練し、その後、未知のデータに対して予測を行い、実際の結果と比較する手法です。予測された分散と実際の分散を比較することで、モデルの予測精度を評価します。

以下、コード例です。

import numpy as np

import pandas as pd

from arch import arch_model

from sklearn.metrics import mean_squared_error

# バックテスト

np.random.seed(42)

data = pd.Series(np.random.randn(1000))

train, test = data[:700], data[700:]

model = arch_model(train, vol='Garch', p=1, q=1)

results = model.fit(disp='off')

forecast = results.forecast(horizon=len(test))

pred = forecast.variance.values[-1]

actual = test.rolling(window=50).var().dropna()

mse = mean_squared_error(actual, pred[:len(actual)])

rmse = np.sqrt(mse)

print(f"RMSE: {rmse}")

import numpy as np import pandas as pd from arch import arch_model from sklearn.metrics import mean_squared_error # バックテスト np.random.seed(42) data = pd.Series(np.random.randn(1000)) train, test = data[:700], data[700:] model = arch_model(train, vol='Garch', p=1, q=1) results = model.fit(disp='off') forecast = results.forecast(horizon=len(test)) pred = forecast.variance.values[-1] actual = test.rolling(window=50).var().dropna() mse = mean_squared_error(actual, pred[:len(actual)]) rmse = np.sqrt(mse) print(f"RMSE: {rmse}")

import numpy as np
import pandas as pd
from arch import arch_model
from sklearn.metrics import mean_squared_error

# バックテスト
np.random.seed(42)
data = pd.Series(np.random.randn(1000))
train, test = data[:700], data[700:]

model = arch_model(train, vol='Garch', p=1, q=1)
results = model.fit(disp='off')

forecast = results.forecast(horizon=len(test))
pred = forecast.variance.values[-1]

actual = test.rolling(window=50).var().dropna()

mse = mean_squared_error(actual, pred[:len(actual)])
rmse = np.sqrt(mse)
print(f"RMSE: {rmse}")

以下、実行結果です。

RMSE: 0.17436399336238564

ヒットレート

予測された分散が実際の分散をどれだけ正確に捉えているかを評価する方法です。具体的には、予測された分散が実際の分散の範囲内に収まる割合を計算します。

以下、コード例です。

from scipy.stats import norm

# ヒットレートの閾値の計算

diff_train = train.rolling(window=50).var().dropna() - results.conditional_volatility[:len(train.rolling(window=50).var().dropna())]

mean_diff_train = np.mean(diff_train)

std_diff_train = np.std(diff_train)

z = norm.ppf(0.975)

upper_threshold = mean_diff_train + z * std_diff_train

lower_threshold = mean_diff_train - z * std_diff_train

# テストデータのヒットレート

diff = pred[:len(actual)] - actual

hit_rate = np.mean((diff >= lower_threshold) & (diff <= upper_threshold))

print(f"Hit Rate: {hit_rate}")

from scipy.stats import norm # ヒットレートの閾値の計算 diff_train = train.rolling(window=50).var().dropna() - results.conditional_volatility[:len(train.rolling(window=50).var().dropna())] mean_diff_train = np.mean(diff_train) std_diff_train = np.std(diff_train) z = norm.ppf(0.975) upper_threshold = mean_diff_train + z * std_diff_train lower_threshold = mean_diff_train - z * std_diff_train # テストデータのヒットレート diff = pred[:len(actual)] - actual hit_rate = np.mean((diff >= lower_threshold) & (diff <= upper_threshold)) print(f"Hit Rate: {hit_rate}")

from scipy.stats import norm

# ヒットレートの閾値の計算
diff_train = train.rolling(window=50).var().dropna() - results.conditional_volatility[:len(train.rolling(window=50).var().dropna())]
mean_diff_train = np.mean(diff_train)
std_diff_train = np.std(diff_train)
z = norm.ppf(0.975) 
upper_threshold = mean_diff_train + z * std_diff_train
lower_threshold = mean_diff_train - z * std_diff_train

# テストデータのヒットレート
diff = pred[:len(actual)] - actual
hit_rate = np.mean((diff >= lower_threshold) &amp; (diff <= upper_threshold))
print(f"Hit Rate: {hit_rate}")

以下、実行結果です。

Hit Rate: 0.9601593625498008

逆分散比率検定

予測された分散と実際の分散の比率を計算し、その逆数を取ることで、予測精度を評価します。この方法は、予測された分散が実際の分散に対してどれだけ過大または過小評価されているかを示します。

以下、コード例です。

# 逆分散比率検定

inverse_variance_ratio = np.mean(actual / pred[:len(actual)])

print(f"Inverse Variance Ratio: {inverse_variance_ratio}")

# 逆分散比率検定 inverse_variance_ratio = np.mean(actual / pred[:len(actual)]) print(f"Inverse Variance Ratio: {inverse_variance_ratio}")

# 逆分散比率検定
inverse_variance_ratio = np.mean(actual / pred[:len(actual)])
print(f"Inverse Variance Ratio: {inverse_variance_ratio}")

以下、実行結果です。

Inverse Variance Ratio: 0.8762250502601119

交差検証

データを複数の部分に分割し、各部分をテストデータとして使用し、残りの部分を訓練データとして使用する方法です。これにより、モデルの予測精度をより一般化された形で評価できます。

以下、コード例です。

from sklearn.model_selection import TimeSeriesSplit

# 交差検証

n_splits = 5

splits = TimeSeriesSplit(n_splits=n_splits)

rmse_scores = []

for train_index, test_index in splits.split(data):

train, test = data[train_index], data[test_index]

model = arch_model(train, vol='Garch', p=1, q=1)

results = model.fit(disp='off')

forecast = results.forecast(horizon=len(test))

pred = forecast.variance.values[-1]

actual = test.rolling(window=50).var().dropna()

mse = mean_squared_error(actual, pred[:len(actual)])

rmse_scores.append(np.sqrt(mse))

mean_rmse = np.mean(rmse_scores)

print(f"Mean RMSE from Cross-Validation: {mean_rmse}")

from sklearn.model_selection import TimeSeriesSplit # 交差検証 n_splits = 5 splits = TimeSeriesSplit(n_splits=n_splits) rmse_scores = [] for train_index, test_index in splits.split(data): train, test = data[train_index], data[test_index] model = arch_model(train, vol='Garch', p=1, q=1) results = model.fit(disp='off') forecast = results.forecast(horizon=len(test)) pred = forecast.variance.values[-1] actual = test.rolling(window=50).var().dropna() mse = mean_squared_error(actual, pred[:len(actual)]) rmse_scores.append(np.sqrt(mse)) mean_rmse = np.mean(rmse_scores) print(f"Mean RMSE from Cross-Validation: {mean_rmse}")

from sklearn.model_selection import TimeSeriesSplit

# 交差検証
n_splits = 5
splits = TimeSeriesSplit(n_splits=n_splits)
rmse_scores = []

for train_index, test_index in splits.split(data):
    train, test = data[train_index], data[test_index]
    model = arch_model(train, vol='Garch', p=1, q=1)
    results = model.fit(disp='off')
    forecast = results.forecast(horizon=len(test))
    pred = forecast.variance.values[-1]
    actual = test.rolling(window=50).var().dropna()
    mse = mean_squared_error(actual, pred[:len(actual)])
    rmse_scores.append(np.sqrt(mse))

mean_rmse = np.mean(rmse_scores)
print(f"Mean RMSE from Cross-Validation: {mean_rmse}")

以下、実行結果です。

Mean RMSE from Cross-Validation: 0.19149435190259217