計算結果をわかりやすく表示することは、ビジネスや教育、技術計算の場面で非常に重要です。特に複雑な数式や計算過程を伝えるとき、視覚的に見やすい形式で表示することが理解を助け、コミュニケーションを円滑にします。ここで役立つのが「Handcalcs」というライブラリです。
Handcalcsを使用するためには、Python環境にライブラリをインストールする必要があります。以下のコマンドをターミナルやコマンドプロンプトで実行してください。
pip install handcalcs
Handcalcsは、Jupyter Notebook内で手書き風の数式を表示するだけでなく、LaTeX形式での数式表示もサポートしています。LaTeXは学術論文や技術レポートで使われる数式フォーマットで、非常に美しい数式を生成するため、プロフェッショナルな場面でも役立ちます。
Jupyter Notebookでの%%renderマジックコマンド
Handcalcsを使う際、Jupyter Notebookなどの環境では、%%renderマジックコマンドを使用して、数式の計算過程を表示することができます。
%%renderは、セル全体で行われた計算を視覚化する便利なコマンドです。これを使うことで、複雑な数式もスムーズに可視化できます。
まず、モジュールを読み込みます。
以下、コードです。
import handcalcs.render
%%renderで、セル全体で行われた計算を視覚化する、簡単な使用例です。
以下、コードです。
%%render x = 10 y = 5 z = x * y
以下、実行結果です。
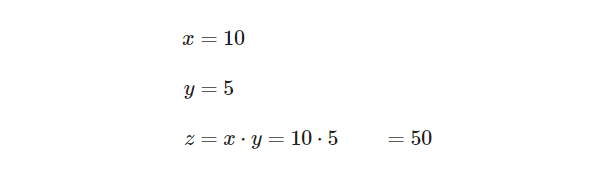
この表示のLaTexコードを出力することもできます。
以下、コードです。
%%tex x = 10 y = 5 z = x * y
以下、実行結果です。LaTexコードです。
\[
\begin{aligned}
x &= 10 \;
\\[10pt]
y &= 5 \;
\\[10pt]
z &= x \cdot y = 10 \cdot 5 &= 50
\end{aligned}
\]
このLaTexコードを表示すると、以下のようになります。
\displaystyle \begin{array}{ll}x &= 10 \; \\[10pt]y &= 5 \; \\[10pt]z &= x \cdot y = 10 \cdot 5 &= 50 \end{array}
@handcalcデコレータを使った数式の表示
@handcalcデコレータを使った基本的な使い方を紹介します。Handcalcsでは、数式をそのまま手書き風に可視化でき、計算結果だけでなく、計算過程もわかりやすく表示することができます。
LaTeX形式の数式を表示するには、@handcalc(jupyter_display=True)を使います。このオプションを指定すると、関数内の計算結果がLaTeX形式で表示されます。
以下、コードです。
from handcalcs.decorator import handcalc
from math import sqrt, pi, exp
@handcalc(jupyter_display=True)
def normal_distribution(mean, variance, x):
std_dev = sqrt(variance)
coefficient = 1 / (std_dev * sqrt(2 * pi))
exponent = exp(-0.5 * ((x - mean) / std_dev) ** 2)
pdf = coefficient * exponent
return pdf
normal_distribution(0, 1, 3)
以下、実行結果です。
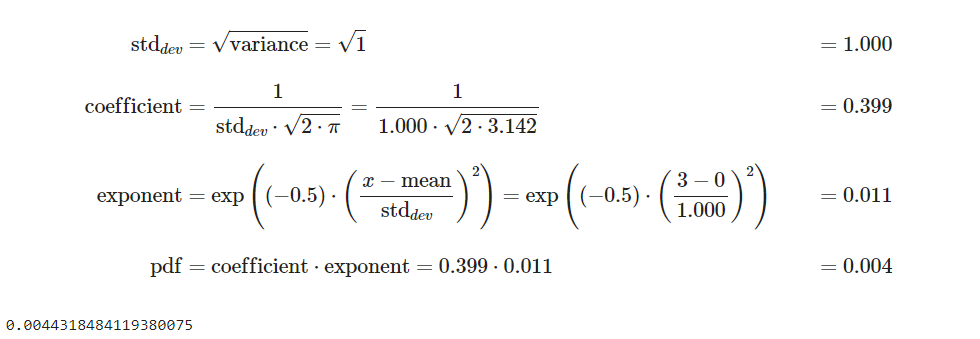
計算で利用する数学の関数はnumpyではなくmathライブラリーのものを利用すると、きれいに表示されます。
次に、LaTexコードと関数の結果を分けて出力します。@handcalc()の引数にjupyter_display=Trueを指定しません。
以下、コードです。
from handcalcs.decorator import handcalc
from math import sqrt, pi, exp
@handcalc()
def normal_distribution(mean, variance, x):
std_dev = sqrt(variance)
coefficient = 1 / (std_dev * sqrt(2 * pi))
exponent = exp(-0.5 * ((x - mean) / std_dev) ** 2)
pdf = coefficient * exponent
return pdf
latex_code, result = normal_distribution(0, 1, 3)
latex_codeにLaTexコードが、resultに関数の結果が格納されています。
resultの中を見てみます。
以下、コードです。
print(result)
以下、実行結果です。
0.0044318484119380075
latex_codeの中を見てみます。
以下、コードです。
print(latex_code)
以下、実行結果です。LaTexコードです。
\begin{aligned}
\mathrm{std}_{dev} &= \sqrt { \mathrm{variance} } = \sqrt { 1 } &= 1.000
\\[10pt]
\mathrm{coefficient} &= \frac{ 1 }{ \mathrm{std}_{dev} \cdot \sqrt { 2 \cdot \pi } } = \frac{ 1 }{ 1.000 \cdot \sqrt { 2 \cdot 3.142 } } &= 0.399
\\[10pt]
\mathrm{exponent} &= \exp \left( \left( - 0.5 \right) \cdot \left( \frac{ x - \mathrm{mean} }{ \mathrm{std}_{dev} } \right) ^{ 2 } \right) = \exp \left( \left( - 0.5 \right) \cdot \left( \frac{ 3 - 0 }{ 1.000 } \right) ^{ 2 } \right) &= 0.011
\\[10pt]
\mathrm{pdf} &= \mathrm{coefficient} \cdot \mathrm{exponent} = 0.399 \cdot 0.011 &= 0.004
\end{aligned}
このLaTexコードを表示すると、以下のようになります。
\displaystyle \begin{array}{ll} \mathrm{std}_{dev} &= \sqrt { \mathrm{variance} } = \sqrt { 1 } &= 1.000 \\[10pt]\mathrm{coefficient} &= \frac{ 1 }{ \mathrm{std}_{dev} \cdot \sqrt { 2 \cdot \pi } } = \frac{ 1 }{ 1.000 \cdot \sqrt { 2 \cdot 3.142 } } &= 0.399 \\[10pt]\mathrm{exponent} &= \exp \left( \left( - 0.5 \right) \cdot \left( \frac{ x - \mathrm{mean} }{ \mathrm{std}_{dev} } \right) ^{ 2 } \right) = \exp \left( \left( - 0.5 \right) \cdot \left( \frac{ 3 - 0 }{ 1.000 } \right) ^{ 2 } \right) &= 0.011 \\[10pt]\mathrm{pdf} &= \mathrm{coefficient} \cdot \mathrm{exponent} = 0.399 \cdot 0.011 &= 0.004 \end{array}
まとめ
Handcalcsは、シンプルでありながら非常に強力なツールです。
計算式の可視化や数式の美しい表示は、ビジネスや教育、技術分野で幅広く活用できます。
より効率的に計算結果を伝えるための手段として、Handcalcsを積極的に活用してください。
