Python 時系列分析 1,000本ノック– ノック72: コレログラム –

問題
答え
解説

次の Python コードを実行した場合に得られる情報は？

Python コード:

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from statsmodels.graphics.tsaplots import plot_acf

np.random.seed(42)

data = pd.Series(np.random.randn(100).cumsum())

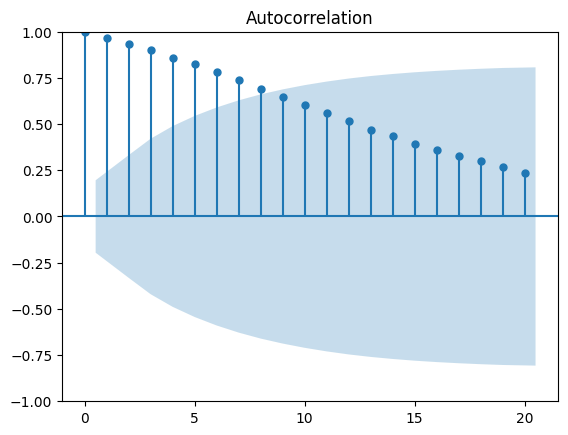
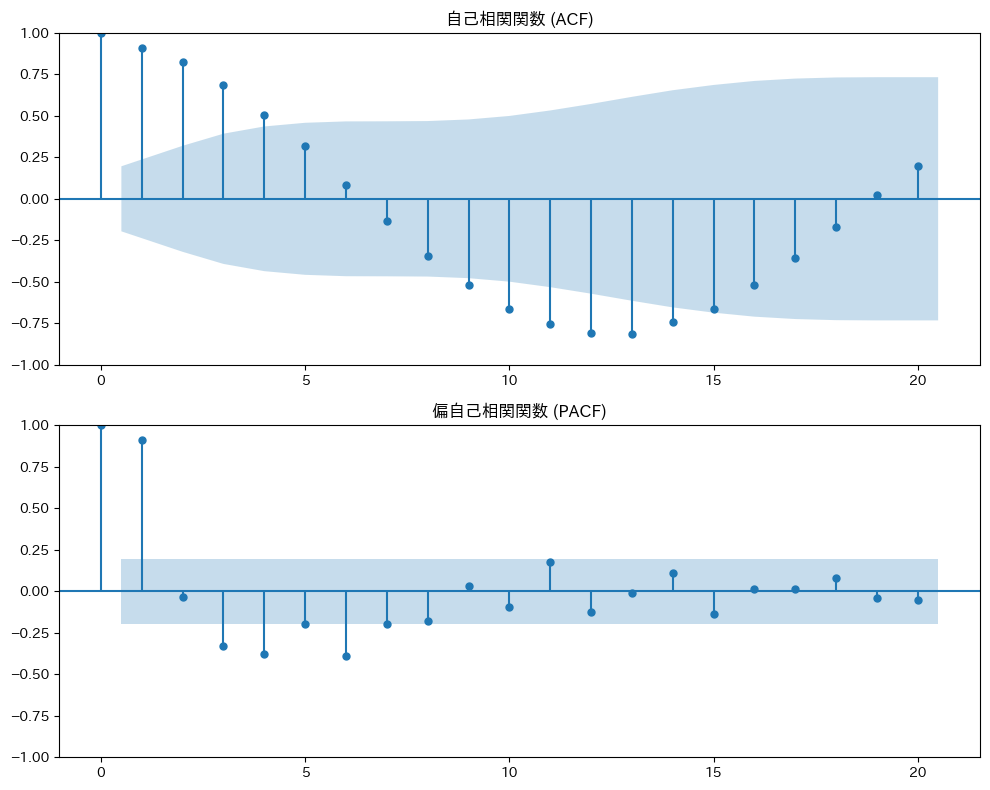
plot_acf(data, lags=20)

plt.show()

import numpy as np import pandas as pd import matplotlib.pyplot as plt from statsmodels.graphics.tsaplots import plot_acf np.random.seed(42) data = pd.Series(np.random.randn(100).cumsum()) plot_acf(data, lags=20) plt.show()

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf

np.random.seed(42)
data = pd.Series(np.random.randn(100).cumsum())

plot_acf(data, lags=20)
plt.show()

回答の選択肢:

(A) 時系列データの分布に関する情報
(B) 時系列データの各ラグ間の相関関係
(C) 時系列データの平均と分散の安定性
(D) 時系列データの長期的なトレンド

出力例:

正解: (B)
このコードは、時系列データの自己相関を視覚化するためのコレログラム（Correlogram）を作成しています。自己相関関数（ACF）は、時系列データ内の異なるラグ間の相関関係を出力関数です。ACFのプロットを見ることで、データに周期性や自己相関の強さがあるかどうかを判断できます。

回答の選択肢:

コードの解説

このコードは、時系列データの自己相関を視覚化するためのコレログラム（Correlogram）を作成しています。

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from statsmodels.graphics.tsaplots import plot_acf

np.random.seed(42)

data = pd.Series(np.random.randn(100).cumsum())

plot_acf(data, lags=20)

plt.show()

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf

np.random.seed(42)
data = pd.Series(np.random.randn(100).cumsum())

plot_acf(data, lags=20)
plt.show()

詳しく説明します。

ライブラリのインポート

numpy と pandas はデータ操作のために使用されます。
matplotlib.pyplot はグラフを描画するために使用されます。
statsmodels.graphics.tsaplots.plot_acf は自己相関関数（ACF: Autocorrelation Function）をプロットするために使用されます。

データの生成

np.random.seed(42) は乱数のシードを設定し、再現性を確保します。
np.random.randn(100).cumsum() はランダムな正規分布に従う100個の値を生成し、それを累積和に変換します。この結果、ランダムウォークのような時系列データが作成されます。
pd.Series を使って、このデータをPandasのシリーズ形式に変換します。

コレログラムの作成

plot_acf(data, lags=20) は、データの自己相関を計算し、ラグ（遅れ）の数を20まで指定してプロットします。
自己相関は、時系列データの現在の値と過去の値との相関を測定します。

グラフの表示

plt.show() を使って、プロットされたコレログラムを表示します。

このコードの結果として、時系列データの自己相関を視覚的に確認できるコレログラムが表示されます。

コレログラムとは？

Contents [hide]

簡単な例を作って見てみよう
自己相関（ACF）とは？
偏自己相関（PACF）とは？
実践的な使い方

簡単な例を作って見てみよう

コレログラムとは、自己相関（ACF）と偏自己相関（PACF）の結果をプロットしたもので、横軸がラグ、縦軸がラグとの相関もしくは偏相関を表します。

ちなみに、例えば「ラグ1との相関」とは「1期前の自分自身との相関」、「ラグ2との相関」とは「2期前の自分自身との相関」、……です。

statsmodelsライブラリのplot_acfとplot_pacfを使って、簡単に作成できます。

以下、コードです。

import numpy as np

import pandas as pd

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

import matplotlib.pyplot as plt

import japanize_matplotlib

# 例として、季節性のある時系列データを作成

np.random.seed(42)

n_points = 100

seasonal_pattern = np.sin(np.linspace(0, 8*np.pi, n_points)) # 周期的なパターン

noise = np.random.normal(0, 0.2, n_points) # ランダムなノイズ

data = seasonal_pattern + noise

# プロットの作成

fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))

# 自己相関（ACF）のプロット

plot_acf(data, lags=20, ax=ax1)

ax1.set_title('自己相関関数 (ACF)')

# 偏自己相関（PACF）のプロット

plot_pacf(data, lags=20, ax=ax2)

ax2.set_title('偏自己相関関数 (PACF)')

plt.tight_layout()

plt.show()

import numpy as np import pandas as pd from statsmodels.graphics.tsaplots import plot_acf, plot_pacf import matplotlib.pyplot as plt import japanize_matplotlib # 例として、季節性のある時系列データを作成 np.random.seed(42) n_points = 100 seasonal_pattern = np.sin(np.linspace(0, 8*np.pi, n_points)) # 周期的なパターン noise = np.random.normal(0, 0.2, n_points) # ランダムなノイズ data = seasonal_pattern + noise # プロットの作成 fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8)) # 自己相関（ACF）のプロット plot_acf(data, lags=20, ax=ax1) ax1.set_title('自己相関関数 (ACF)') # 偏自己相関（PACF）のプロット plot_pacf(data, lags=20, ax=ax2) ax2.set_title('偏自己相関関数 (PACF)') plt.tight_layout() plt.show()

import numpy as np
import pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
import japanize_matplotlib

# 例として、季節性のある時系列データを作成
np.random.seed(42)
n_points = 100
seasonal_pattern = np.sin(np.linspace(0, 8*np.pi, n_points))  # 周期的なパターン
noise = np.random.normal(0, 0.2, n_points)  # ランダムなノイズ
data = seasonal_pattern + noise

# プロットの作成
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))

# 自己相関（ACF）のプロット
plot_acf(data, lags=20, ax=ax1)
ax1.set_title('自己相関関数 (ACF)')

# 偏自己相関（PACF）のプロット
plot_pacf(data, lags=20, ax=ax2)
ax2.set_title('偏自己相関関数 (PACF)')

plt.tight_layout()
plt.show()

以下、実行結果です。