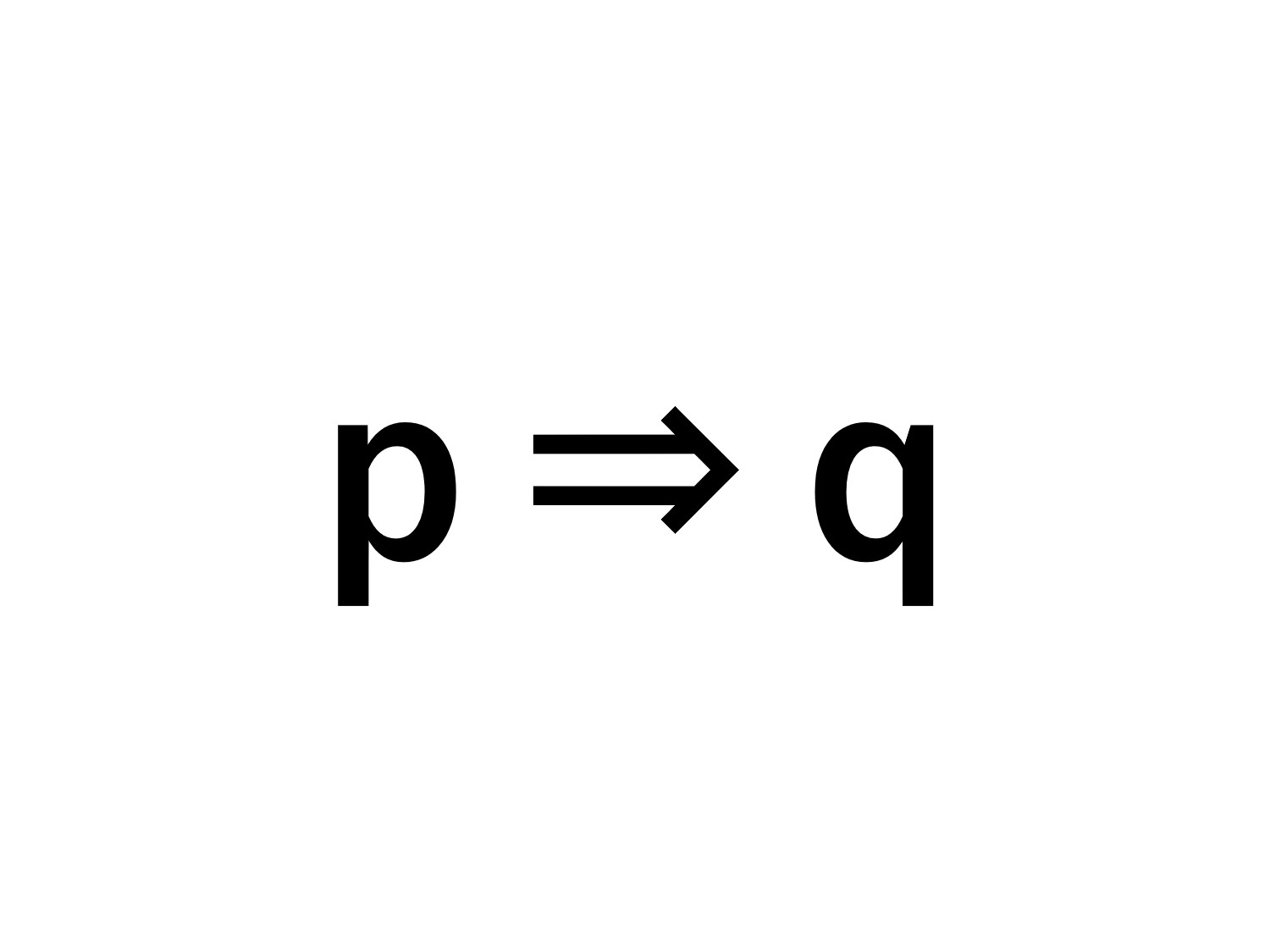ジョン・スチュアート・ミルの著書『論理学体系』の中に、因果関係の問題を解明するための5つの方法論があります。
その中で、簡単で知っていて損のないのが、「一致法」と「差異法」です。
現代のデータ分析だけでなく、ビジネス上のスキルとしても有効です。
今回は、「古くても知っていて損のないミルの比較分析(一致法と差異法など諸々)」というお話しをします。
Contents [hide]
ジョン・スチュアート・ミルの著書『論理学体系』

論理学が、哲学なのか数学なのかわかりませんが、『論理学体系』は哲学者のイメージの強いジョン・スチュアート・ミルが19世紀に執筆し出版した書籍です。
因果関係を解明するための5つの方法が述べられています。
- 一致法(method of agreement)
- 差異法(method of difference)
- 共変法(method of concomitant variations)
- 一致差異併用法(joint method of agreement and difference)
- 剰余法(method of residues)
その中で知っていて損がなく、比較的簡単に理解できるのが以下の2つです。
- 一致法(method of agreement)
- 差異法(method of difference)
簡単に言うと、高校数学(確か高校1年生)で登場する、「必要条件」と「十分条件」に関するものです。
単に、定性的に物事を分析するときに、非常に有効です。
定量的なデータ分析の「結果」も、その「結果」は定性的に人間が分析する必要があるため、定量的なデータ分析をする人も、知っていて損はありません。
「必要条件」と「十分条件」

「必要条件」や「十分条件」というワードを聞くと、頭痛のする人もいるかもしれません。
雰囲気だけ掴んでもらえればと思います。
一般的には……
- 条件「p」と「q」があるとする
- 「p⇒q」が真であるとする
- qは、pであるための必要条件
- pは、qであるための十分条件
……といった感じでしょうか。
海に生息するタコ(蛸)で考えてみます。
- p:タコ
- q:軟体動物
このとき……
- p⇒q
……は「タコは軟体動物である」ということを示しています。
逆にするとどうでしょうか。
- q⇒p
これは、「軟体動物はタコである」となり可笑しいですね。なぜならば、タコ以外にも軟体動物が存在するからです。
要するに……
- p:タコ
- q:軟体動物
のとき……
- p⇒q
となり……
- 軟体動物(q)は、タコ(p)であるための必要条件
- タコ(p)は、軟体動物(q)であるための十分条件
となります。
もう少し砕けた言い方をすると……
- 色々な軟体動物(q)がいるが、その中にタコ(p)もいる
- タコ(p)であるならば、それは軟体動物(q)である
ビジネス的に「十分条件」を考える

新規受注のためのマーケティング&営業活動を実施しているとしましょう。
このとき、新規受注のための「十分条件」が分かると嬉しいです。
- 十分条件 ⇒ 新規受注
新規受注のための「十分条件」とは、受注するための条件のことです。
データ分析や数理モデル的に考えれば、受注するための「説明変数の値」になります。
受注の予測モデルという視点で考えると、受注確率に効いている「説明変数」のことです。
「十分条件」は、本来であれば100%受注となりますが、現実はそうはならないので、「十分条件のような説明変数」といったところです。
ビジネス的に「必要条件」を考える

同じ例で、「必要条件」の場合はどうでしょうか。
- 新規受注 ⇒ 必要条件
新規受注顧客を調べてみたら、ある共通の特徴を見いだせることは、よくあります。
この共通の特徴が、「必要条件」です。
例えば……
- この商材Aは、大手建設業に売れている
- この商品Bは、20代女性の購入者が多い
- このサービスCは、地方の小規模な小売りが定期購入している
……などです。
このとき……
- 商材Aの新規受注 ⇒ 大手建設業
であっても……
- 大手建設業 ⇒ 商材Aの新規受注
ではないということです。
商材Aの新規受注顧客の特徴として「大手建設業」があげられるが、大手建設業であれば必ず新規受注できるわけではないし、新規受注確率が必ずしも高いわけでもない、ということです。
必要条件を炙り出す「一致法」
前置きが長くなりましたが、ジョン・スチュアート・ミルの「一致法」です。
「一致法」とは、必要条件を炙り出す方法です。
具体的には、同じ結果(例:新規受注)を示す複数の事例(例:新規受注顧客の属性など)を比較し、共通する要因(例:大手建設業)を探ります。
要するに、共通の結果(例:新規受注)をもたらした要因(例:新規受注顧客の属性など)を考える方法です。
十分条件を炙り出す「差異法」
ジョン・スチュアート・ミルの「差異法」です。
「差異法」とは、十分条件を炙り出す方法です。
具体的には、異なる結果(例:受注と失注)を比較します。
異なる結果(例:受注と失注)を比較したとき、異なる要因(例:新規受注顧客の属性など)があれば、それが結果の違いを生み出すものと考えます。
あなたのデータ分析は「一致法」的? 「差異法」的?
定量的なデータ分析であっても、その分析結果を解釈するとき、おそらく「一致法」もしくは「差異法」のどちらかの観点で解釈することが、多いと思います。
端的に述べれば、新規受注顧客の特徴を探る分析であれば、それは「一致法」的でしょう。
新規受注予測モデルを構築するためのデータ分析であれば、それは「差異法」的でしょう。
データ分析や数理モデル構築の世界の場合、「十分条件」や「必要条件」というものを明確に特定することはできませんが、どちらのことをデータで語らせようとしているのかを明確にしたほうがいいでしょう。
最悪なのは、「十分条件」と「必要条件」を混同することです。
例えば、「この商材Aは、大手建設業に売れている」だから「大手建設業に対し積極的に営業をしろ!」という感じです。
今回のまとめ
今回は、「古くても知っていて損のないミルの比較分析(一致法と差異法など諸々)」というお話しをしました。
ジョン・スチュアート・ミルの著書『論理学体系』の中に、因果関係の問題を解明するための5つの方法論があります。
- 一致法(method of agreement)
- 差異法(method of difference)
- 共変法(method of concomitant variations)
- 一致差異併用法(joint method of agreement and difference)
- 剰余法(method of residues)
その中で知っていて損がなく、比較的簡単に理解できるのが以下の2つです。
- 一致法(method of agreement)
- 差異法(method of difference)
簡単に言うと、高校数学(確か高校1年生)で登場する、「必要条件」と「十分条件」に関するものです。
「一致法」とは、同じ結果(例:新規受注)を示す複数の事例(例:新規受注顧客の属性など)を比較します。そこに共通する要因(例:大手建設業)を探ります。要するに、共通の結果(例:新規受注)をもたらした要因(例:新規受注顧客の属性など)を考える方法です。
この共通の結果をもたらした要因が必要条件です。
「差異法」とは、異なる結果(例:受注と失注)を比較します。異なる結果(例:受注と失注)を比較したとき、異なる要因(例:新規受注顧客の属性など)があれば、それが結果の違いを生み出すものと考えます。
この結果に違いをもたらす要因が十分条件です。
データ分析や数理モデル構築の世界の場合、「十分条件」や「必要条件」というものを明確に特定することはできませんが、どちらのことをデータで語らせようとしているのかを明確にしたほうがいいでしょう。
例えば、新規受注顧客の特徴を探る分析であれば、それは「一致法」的でしょう。新規受注予測モデルを構築するためのデータ分析であれば、それは「差異法」的でしょう。
最悪なのは、「十分条件」と「必要条件」を混同することで、例えば「この商材Aは、大手建設業に売れている」だから「大手建設業に対し積極的に営業をしろ!」という感じです。