AutoML【TPOT】で回帰問題を解く

3931
AutoML【TPOT】で回帰問題を解く

TPOTは分類と回帰の問題を解くことができます。

前回の第3回は分類問題を扱いました。

今回は回帰問題に挑戦します。前回同様JupyterNotebookを使います説明しています。

回帰問題ですので、目的変数Yは……

  • 受注金額
  • 売上個数

……などの数値になります。

そのまま、売上などの数値を予測するのに使えます。

このような予測をするための数理モデルを、TPOTを使い自動で構築してみます。

データセットの説明

今回はscikit-learnから提供されているカリフォルニアの住宅価格データセットを使って解いてみようと思います。

【今回使用】
scikit-learnから提供されているサンプルデータセット
https://scikit-learn.org/stable/datasets/index.html#california-housing-dataset

目的変数Y

目的変数は、カリフォルニアの予測したい区画ごとの住宅価格の中央値です。

データ数は20640件です。

特徴量（説明変数X）

特徴量が8個です。

項目名 詳細
MedInc 予測したい区画の収入の中央値
HouseAge 予測したい区画の築年数
AveRoom 予測したい区画の家の部屋数の平均値
AveBedrms 予測したい区画の寝室の平均値
Population 予測したい区画の人口
AveOccup 予測したい区画の平均入居率
Latitude 予測したい区画の緯度
Longitude 予測したい区画の経度

回帰問題の解き方

プログラムの流れは次のとおりです。

  1. 必要なライブラリの読み込み
  2. データセットの読み込み
  3. データセットを学習用と検証用に分割する
  4. TPOTRegressorの設定
  5. 学習用データセットを使った機械学習モデルの学習
  6. 検証用データセットを使った予測結果の評価

分類問題との大きな違いは、「TPOTClassifier」（分類）ではなく「TPOTRegressor」（回帰）を使うところです。

１．必要なライブラリの読み込み

機械学習モデルを作るために必要なライブラリ一式を読み込んでおきます。

読み込むライブラリは……

  • 回帰問題を解くためのTPOTRegressorモジュール
  • データセットのfetch_california_housing
  • データセットを学習用と検証用に分割するtrain_test_split
  • 精度を算出するためのr2_scoreモジュール
  • 数値計算モジュールであるNumPy
  • データ解析モジュールであるpandas

……です。

前回の分類問題との違いは２点ありあります。

  • TPOTClassifierをTPOTRegressorに変えたところ
  • データセットを分類問題用のload_breast_cancerから回帰問題用のfetch_california_housingへ変えたところ

以下、コードです。

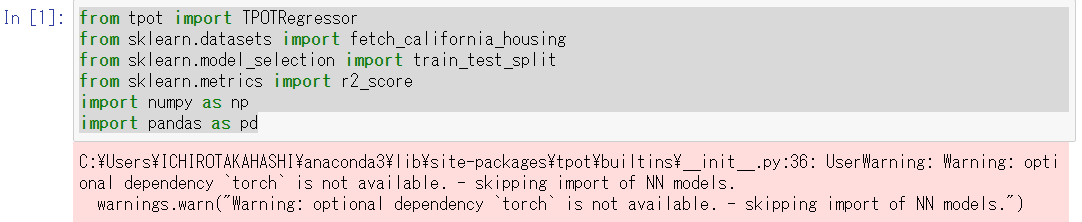
from tpot import TPOTRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
import numpy as np
import pandas as pd

 

以下、実行結果です。

※Torchがインストールされていない場合
上記のようなWarningメッセージが
でますが、今回は問題ありません。

２．データセットの読み込み

機械学習モデルを作りたいデータを読み込み、特徴量をXに、目的変数をyに格納します。

  • 特徴量（説明変数）であるfetch_california_housing.dataをXに格納
  • 目的変数であるfetch_california_housing.targetをyに格納

データセットの説明
https://scikit-learn.org/stable/modules/generated/sklearn.datasets.fetch_california_housing.html#sklearn.datasets.fetch_california_housing

 

以下、コードです。

california_housing = fetch_california_housing(as_frame=True)
X = california_housing.data
y = california_housing.target
　補足事項（scikit-learnのバージョン）　

scikit-learnのバージョンが0.23以上でないと、データフレーム型としてデータを読み込めません。バージョンが0.23以上でない場合には、最新のscikit-learnにアップグレードして頂ければと思います。

アップグレードの方法は、前回に説明しいますので、ご確認ください。

 

TPOTで使える特徴量は数字と欠損値です。文字列は扱えませんので、ダミー変数を作って数値化しておきましょう。今回使うデータセットはすべて数字を使っているので、ダミー変数は作っていません。

特徴量Xとyの中身を少し見てみましょう。

 

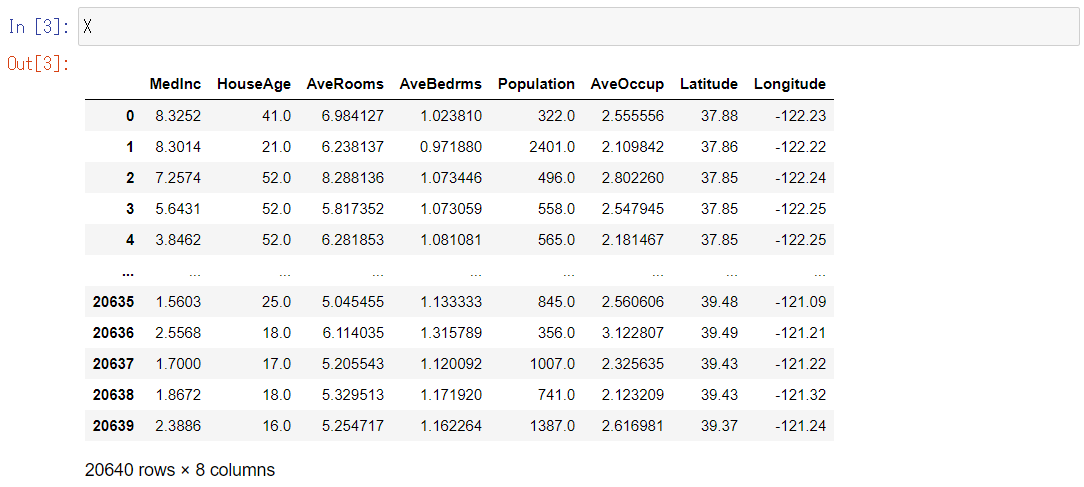
先ずは、特徴量であるXです。

以下、コードです。

X

 

以下、実行結果です。

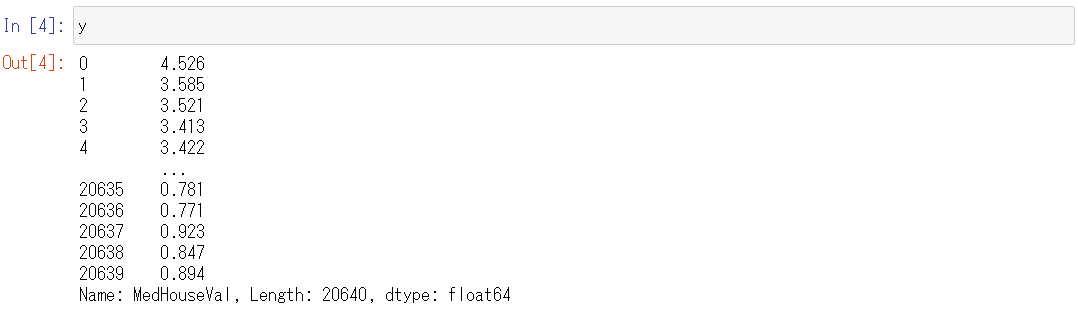
次に、目的変数であるyを見てみます。

以下、コードです。

y

 

以下、実行結果です。

 

また、isna関数とsum関数を使うことで、列ごとに欠損値が存在するかどうかを確認することができます。

  • isna()関数は欠損値の場合Trueを返す
  • sum関数はTrueの数を返す

結果的に、列ごとの欠損値の数を計算できます。

以下、コードです。

print('X')
print(X.isna().sum())
print()
print('y')
print(y.isna().sum())

 

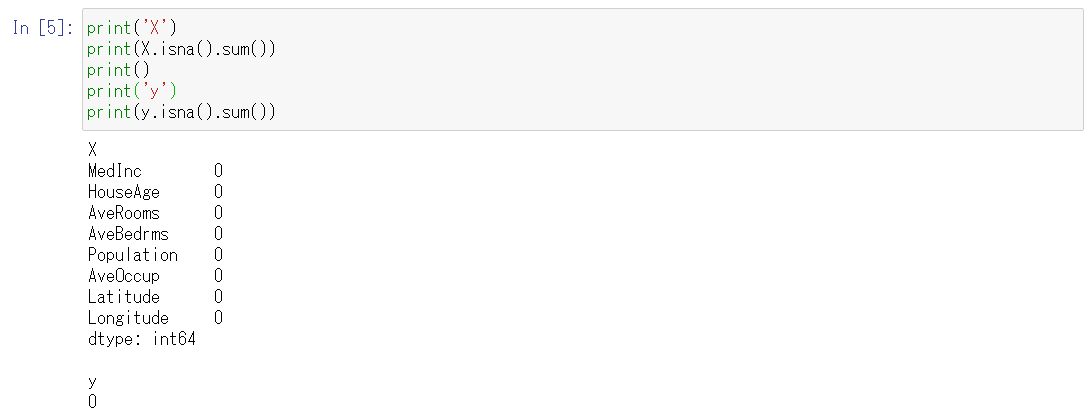
以下、実行結果です。

このデータセットではどの列も0なので、欠損値は存在しないことがわかります。

dtype属性を使うと、各列のデータ型を調べることができます。

以下、コードです。

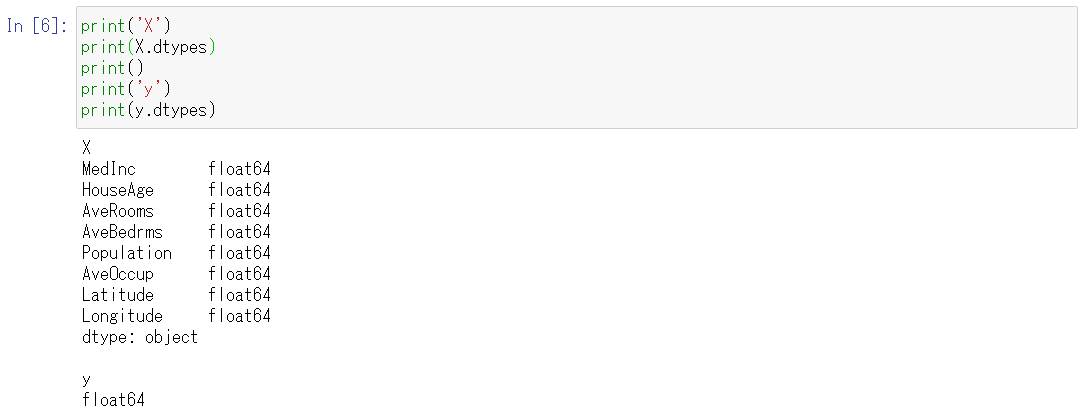
print('X')
print(X.dtypes)
print()
print('y')
print(y.dtypes)

 

以下、実行結果です。

 

すべて数値型で、倍精度浮動小数点型（float64）であることがわかります。

TPOTは数値データを扱うことができるので、このまま使います。

３．データセットを学習用と検証用に分ける

数理モデルを作成するときは、モデルが一定の性能を満たしているか検証するために、データセットを「学習用のデータセット」と「検証用のデータセット」にわけておきます。

  • 学習用のデータセット
    • 学習用の特徴量をX_trainに格納
    • 学習用の目的変数をy_trainに格闘
  • 検証用のデータセット
    • 検証用の特徴量をX_testに格納
    • 検証用の目的変数をy_testに格闘

今回は学習用のデータを75%、検証用のデータを25%に分けます。

以下、コードです。

X_train, X_test, y_train, y_test = train_test_split(X,
                                                    y,
                                                    train_size=0.75,
                                                    test_size=0.25,
                                                    random_state=42)

 

X_trainの中身をみてみましょう。

以下、コードです。

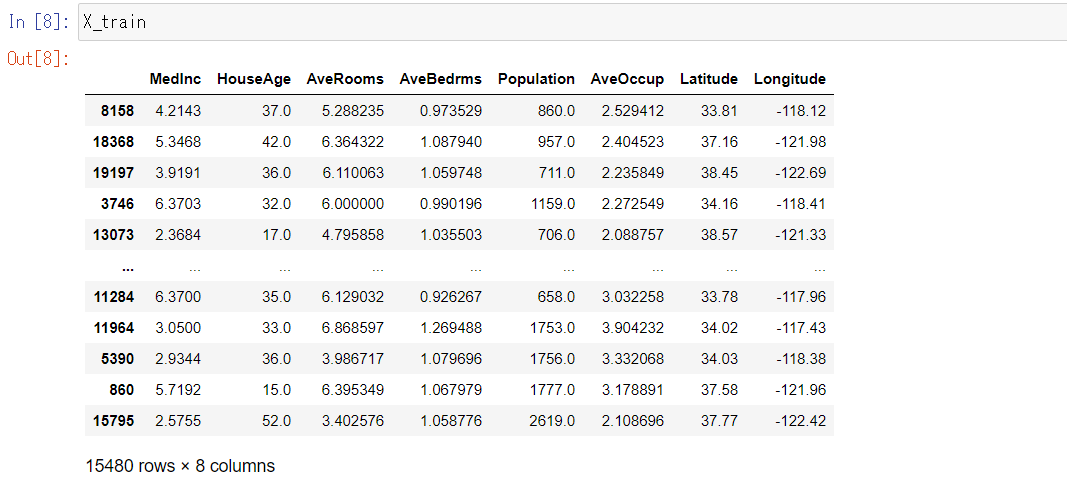
X_train

 

以下、実行結果です。

 

まず、インデックスがランダムになっているので、ランダムに学習データが得られたことがわかります。

さらにデータ数が15,480件で、元データの75%が得られたことがわかります。

 

次にy_trainの中身をみてみましょう。

以下、コードです。

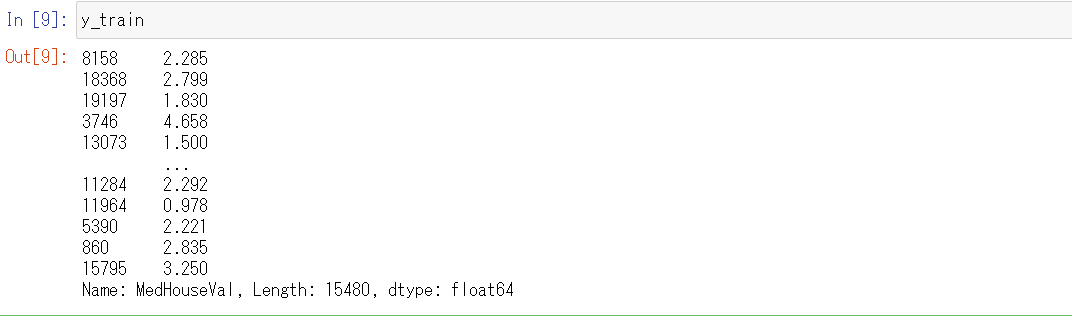
y_train

 

以下、実行結果です。

X_trainとy_trainをそれぞれ比較すると、インデックスが一致しているので、一対一対応していることもわかります。

ここまでが前準備でした。

４．TPOTRegressorの設定

TPOTRegressorの設定をします。

以下、コードです。

tpot = TPOTRegressor(scoring='r2',
                     generations=5,
                     population_size=25,
                     random_state=42,
                     verbosity=2,
                     n_jobs=-1)

 

すべて初期値のままでも動作しますが、scoringパラメータの設定をしておくと良いでしょう。

  • scoringパラメータでは、回帰問題のどの評価指標を用いてモデルを最適化するかを指定することができます。ここの例ではr2スコア（決定係数R2）を使います。指定できる評価指標は多数ありますので、TPOTのリファレンスページの（http://epistasislab.github.io/tpot/api/）Parameters>scoringの説明文をご覧ください。
  • random_stateパラメータは乱数の種です。値を指定しておくと、毎回同じ学習結果が得られます。指定しなければ、毎回少し違った学習結果になります。
  • generationsパラメータでは特徴量の最適化とパラメータチューニングの最適化を何回繰り返すかを指定できます。
  • population_sizeではTPOTが使っている遺伝的アルゴリズム内のパラメータです。
  • verbosityパラメータは進捗状況を表示させるためのもので、プログレスバーを表示させる場合には2を設定します。
  • n_jobsパラメータは並列演算を実施するためのもので、CPUのコア数を最大限に活用する場合には-1を設定します。

generationsパラメータとpopulation_sizeパラメータの数が大きくなれば学習に時間がかかりますので、開発時には小さい数を設定しておくと良いでしょう。

本番の学習ではgenerationsパラメータとpopulation_sizeパラメータを初期値のままにしておくと、最も良い学習をしてくれます。

５．学習用データセットを使った機械学習モデルの学習

tpot.fit関数を使ってモデルを学習します。

関数の引数として、学習用の特徴量X_trainと目的変数y_trainを指定します。

学習には少し時間がかかります。

以下、コードです。

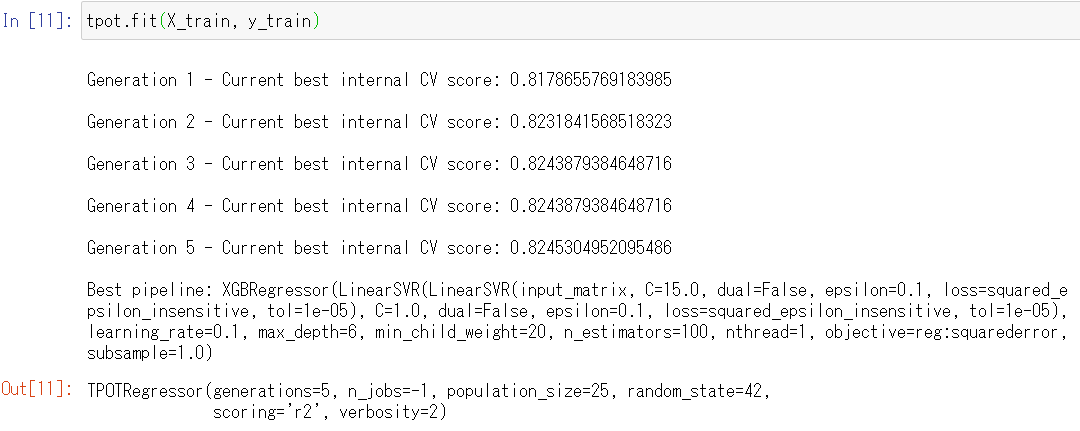
tpot.fit(X_train, y_train)

 

以下、実行結果です。

 

最終的な検討結果（数理モデル）を知りたい場合には、次のコードを入力し実行します。

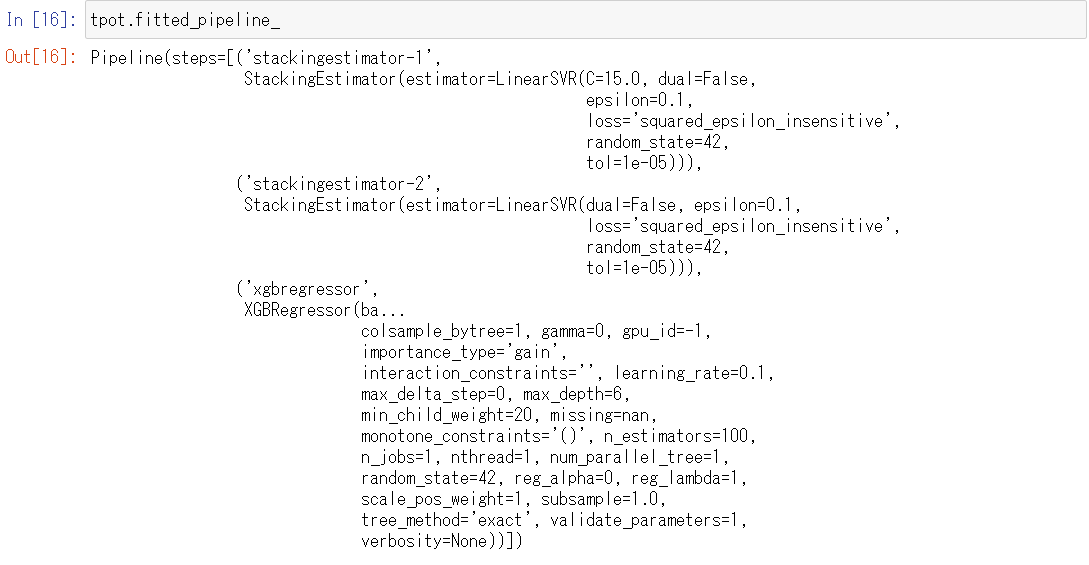
tpot.fitted_pipeline_

 

以下、実行結果です。

 

今回の例ですと、2種類の「線形サポートベクターマシン回帰」（LinearSVR）と「XGBoost回帰」（XGBRegression）をスタッキング（stacking）した数理モデルを構築するのが、検討した結果最良であるということになります。

スタッキング（stacking）とは、複数のモデル（学習器）を融合させて1つの学習モデルを生成するアンサンブル学習の1つで、モデルを積み上げていく方法（詳細は説明は省きます）です。アンサンブル学習には、スタッキングの他にバギング（Bagging=Bootstrap Aggregating）とブースティング（Boosting）という方法もあります。スタッキングは、アンサンブル学習の中では最も難易度が高く、恐らくブラックボックス度の高い手法です。

６．検証用データセットを使った予測結果の評価

最後は学習済みモデルの検証です。

検証用データセットをできたモデルで予測してみて、回帰モデルの評価指標の一つである決定係数R2を計算します。

R2が望む性能を満たせば機械学習モデルの作成は完了です。

以下、コードです。

y_pred = tpot.predict(X_test)

 

具体的にどのように予測され、どのぐらいの精度が出たかを見てみます。

検証データに格納されている正解データ（y_test）と、検証データで予測した結果（y_pred）を散布図で比較してみます。

以下、コードです。

import matplotlib.pyplot as plt
plt.figure(figsize=(5, 5))
plt.scatter(y_pred,y_test,alpha=0.5)
plt.xlabel('y_pred')
plt.ylabel('y_test')

 

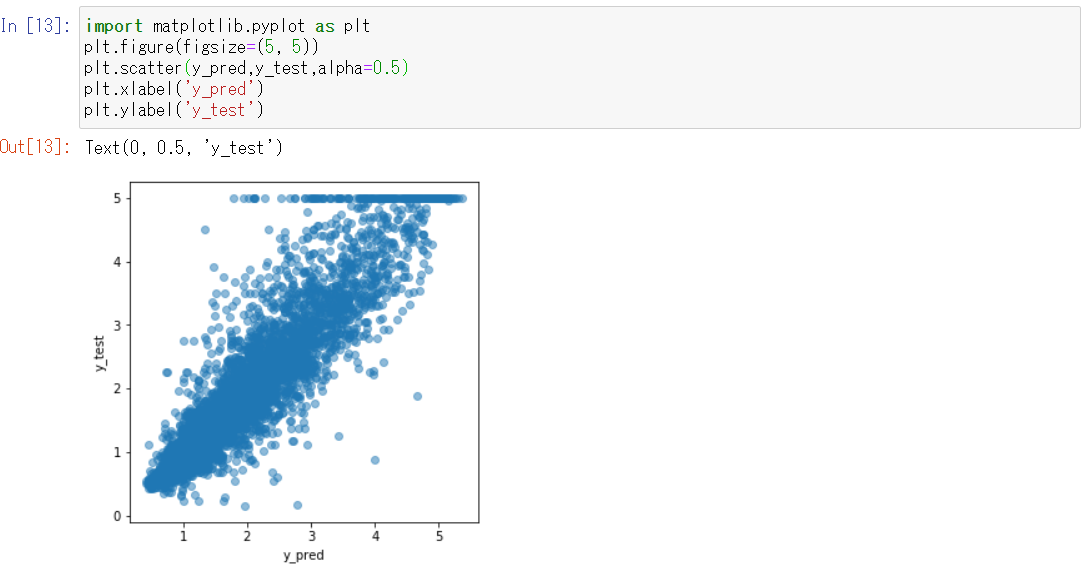
以下、実行結果です。

やや膨らんでいますが、y_pred=y_testとなる線の付近にプロットされているのがわかります。

ただ、y_pred=y_testの線のやや左側にプロットが寄っていることと、y_test=5のプロットがうまく予測できていないので、まだ改善の余地はありそうです。

 

決定係数R2を計算してみます。

以下、コードです。

r2_score(y_true=y_test, y_pred=y_pred)

 

以下、実行結果です。

 

決定係数R2を計算してみると、0.80以上となり、良い結果が得られていることがわかります。

この値がほかの機械学習モデルと比較すると良いのかどうかはまた別の回でご紹介します。

ソースコードの全体像

#１．必要なライブラリの読み込み
from tpot import TPOTRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
import numpy as np
import pandas as pd

#２．データセットの読み込み
california_housing = fetch_california_housing(as_frame=True)
X = california_housing.data
y = california_housing.target

#３．データセットを学習用と検証用に分割する
X_train, X_test, y_train, y_test = train_test_split(X,
                                                    y,
                                                    train_size=0.75,
                                                    test_size=0.25,
                                                    random_state=42)

#４．TPOTRegressorの設定
tpot = TPOTRegressor(scoring='r2',
                     generations=5,
                     population_size=25,
                     random_state=42,
                     verbosity=2,
                     n_jobs=-1)

#５．学習用データセットを使った機械学習モデルの学習
tpot.fit(X_train, y_train)

#６．検証用データセットを使った予測結果の評価
y_pred = tpot.predict(X_test)
r2_score(y_true=y_test, y_pred=y_pred)

 

次回

次回はTPOTの学習結果を別のプログラムから呼び出し、予測する方法を説明します。

AutoML【TPOT】で構築したモデルを他のプログラムで使う