さて、TPOTは自動で特徴量生成と選択、モデル選択をしてくれます。
実際にどのような特徴量が作られ、どのモデルが使われたのか確認したいときがあります。
今回は、第3回で取り上げた分類問題を題材に、TPOTが生成した特徴量と選択したモデルを確認してみます。
前回の復習
前回「TPOTがするのは特徴量と予測モデルの自動生成」というお話しをしました。
ここで簡単に復習します。
「自動機械学習」(AutoML)であるTPOTが実施するのは、以下の2点です。
- 変換器(特徴量の生成と選択)の生成
- 予測器(予測モデル)の生成
変換器(特徴量の生成と選択)と予測器(予測モデル)を直列に繋げたものを「パイプライン」と言います。
データセット
↓
処理プログラム(変換器)
↓
:
↓
処理プログラム(変換器)
↓
処理プログラム(予測器)
↓
予測結果
変換器(特徴量の生成と選択)は1つではなく複数の場合も多いです。
最終的に生成された特徴量および予測モデルの確認方法
パイプラインは、「学習済TPOTClassifier」のfitted_pipeline_属性で確認できます。
第3回でも使った乳がんの診断結果のデータセットを例に、作成された特徴量と使われた予測モデルの確認方法を説明します。
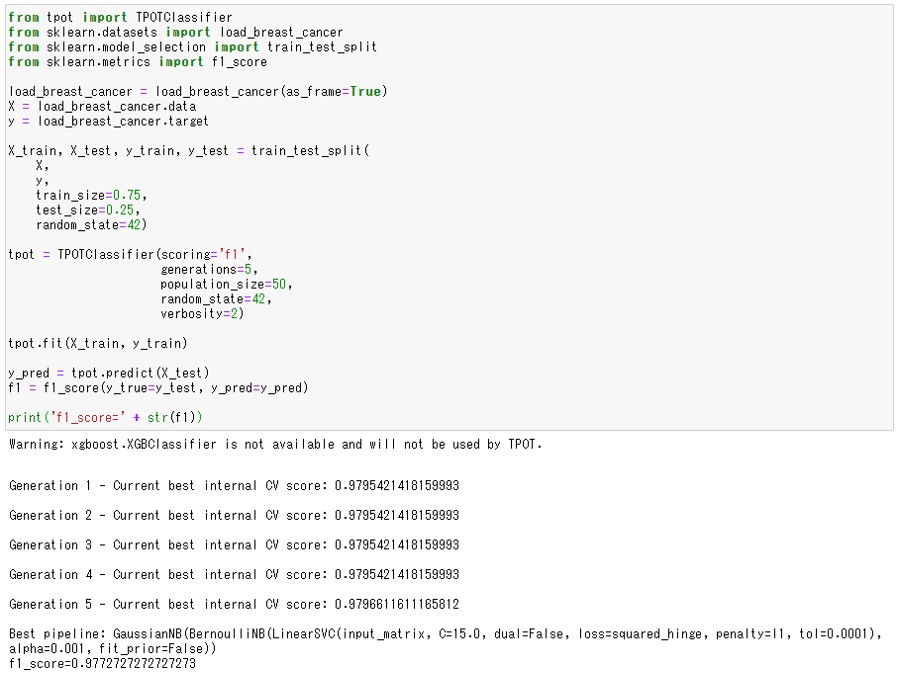
先ずは、TPOTによる学習を済ませます。第3回の次のプログラムをJupyterNotebook上で実行しておきます。
#1.必要なライブラリの読み込み from tpot import TPOTClassifier from sklearn.datasets import load_breast_cancer from sklearn.model_selection import train_test_split from sklearn.metrics import f1_score from sklearn.metrics import confusion_matrix import numpy as np import pandas as pd #2.データセットの読み込み load_breast_cancer = load_breast_cancer(as_frame=True) X = load_breast_cancer.data y = load_breast_cancer.target #3.データセットを学習用と検証用に分割する X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75, test_size=0.25, random_state=42) #4.TPOTClassifierの設定 tpot = TPOTClassifier(scoring='f1', generations=5, population_size=50) #5.学習用データセットを使った機械学習モデルの学習 tpot.fit(X_train, y_train) #6.検証用データセットを使った予測結果の評価 y_pred = tpot.predict(X_test) f1_score(y_true=y_test, y_pred=y_pred)
以下、実行結果です。
結果はf1_score=0.98と非常に良い分類ができていることがわかります。
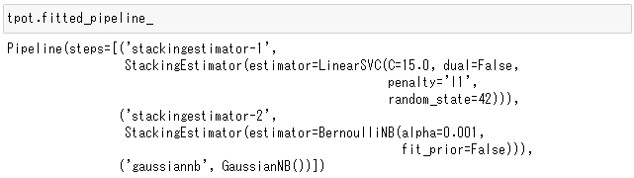
特徴量の生成方法と使われたモデルは、tpotのfitted_pipeline_属性に格納されています。
次のコマンドをJupyterNotebookに入力してください。
tpot.fitted_pipeline_
以下、実行結果です。
実行結果は、TPOTを実行したタイミングや環境などによって変わります。乱数を使った遺伝的アルゴリズムを利用し最適なパイプラインを探索しているためです。
この例では、LinearSVC・BernoulliNB・GaussianNBの3つの関数(今回の場合は、数理モデル)でパイプラインが構成されていることがわかります。
ちなみに、この例のパイプラインは、正直に言うと「やや複雑で説明するには難しいパイプライン」です。通常はもっとシンプルなものが多いです。
では、説明します。
構築された最適なパイプラインの説明
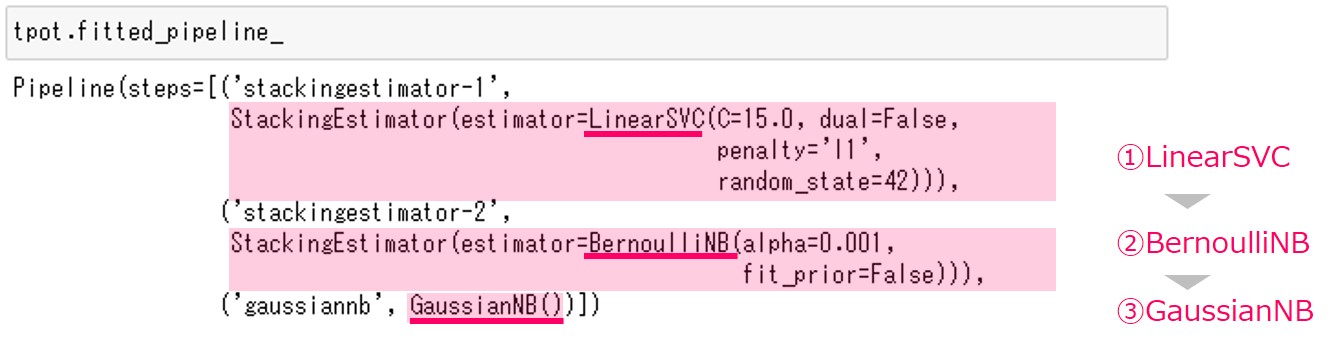
先ほど説明しましたが、LinearSVC・BernoulliNB・GaussianNBの3つの関数(今回の場合は、数理モデル)でパイプラインが構成されています。
- LinearSVC … 線形サポートベクターマシーン。線形分離可能なデータを分類する手法です。
- BernoulliNB … 入力がバイナリデータ(0 or 1)のナイーブベイズ分類器。0か1かの2値分類を行います。
- GaussianNB … 入力が連続値のナイーブベイズ分類器。0か1かの2値分類を行います。
GaussianNBが予測モデル(予測器)で、LinearSVCとBernoulliNBはTPOTのStackingEstimatorを使った変換器になります。
LinearSVCとBernoulliNBは、通常は予測モデル(予測器)ですが、この例では変換器(特徴量の生成と選択)として使うということです。
面白いですね。
このStackingEstimatorは、分類問題の場合、2つの特徴量の生成パターンがあります。
- パターン1 … 分類結果(例:0 or 1 の分類結果)を返す
- パターン2 … 分類結果(例:0 or 1 の分類結果)と分類確率(例:0の分類確率、1の分類確率など)を返す
今回は……
- LinearSVCは分類結果だけを返します(パターン1)
- BernoulliNBは分類結果と分類確率を返します(パターン2)
どちらのパターンなのかは、数理モデルによります。このStackingEstimatorの動作についてはまた別の回で詳しくご説明します。
これはあくまでも一例です。先ほど申しましたが、TPOTのような乱数を使ったAutoML(自動機械学習)の場合、パイプラインは学習のたびに変わることがあります。また、データセットが変われば当然大きく結果が変わります。
今回の例ですと、先ほど申しましたが、変換器に本来は予測で使う数理モデル(予測モデル)を使っています。数理モデルを使っているということは、学習データなどで変換器を学習し構築する必要がでてきます。
そこで、学習と予測に分けてパイプラインの仕組みを説明したいと思います。
ちなみに、よくある変換器は変数変換(例:標準化や対数変換など)を実施するだけのものが多く、変換器の学習という処理はないケースが多いです。
では、説明します。
パイプラインの学習
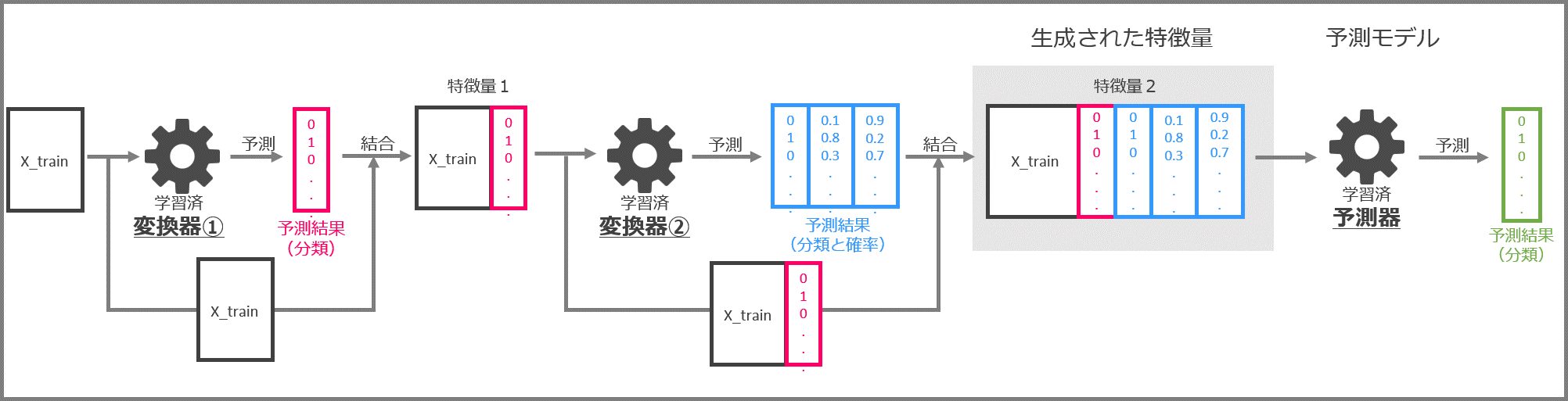
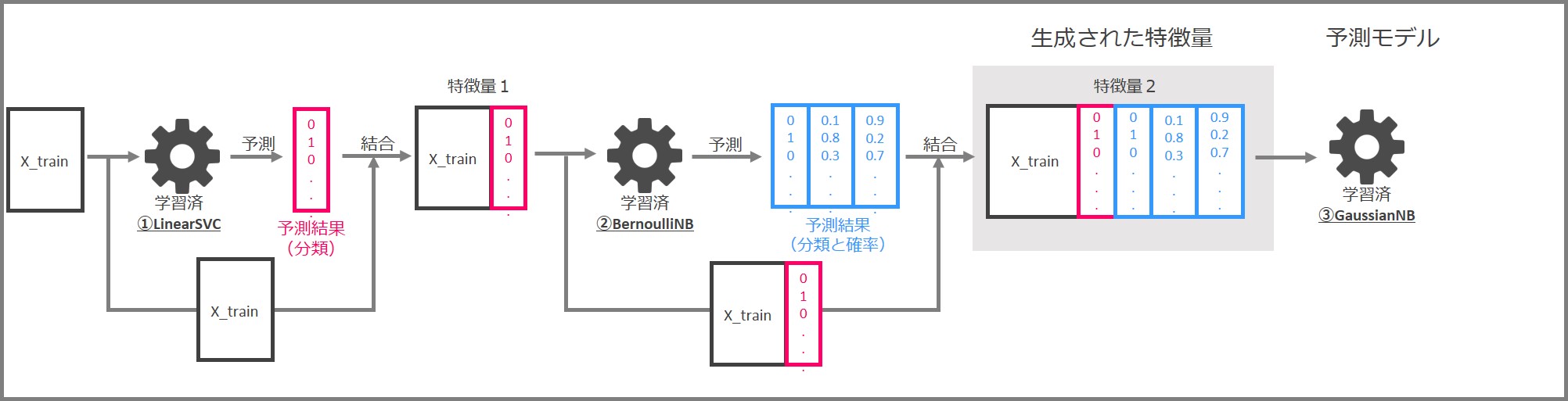
今回の学習済みのパイプラインは、次のようになっています。
この中身を具体的に見ていきます。
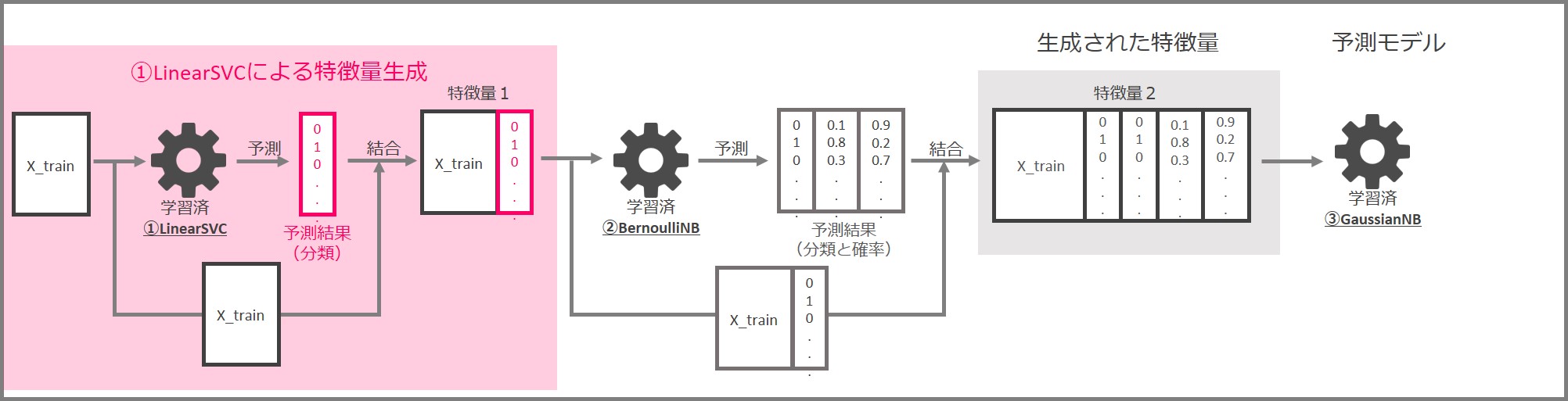
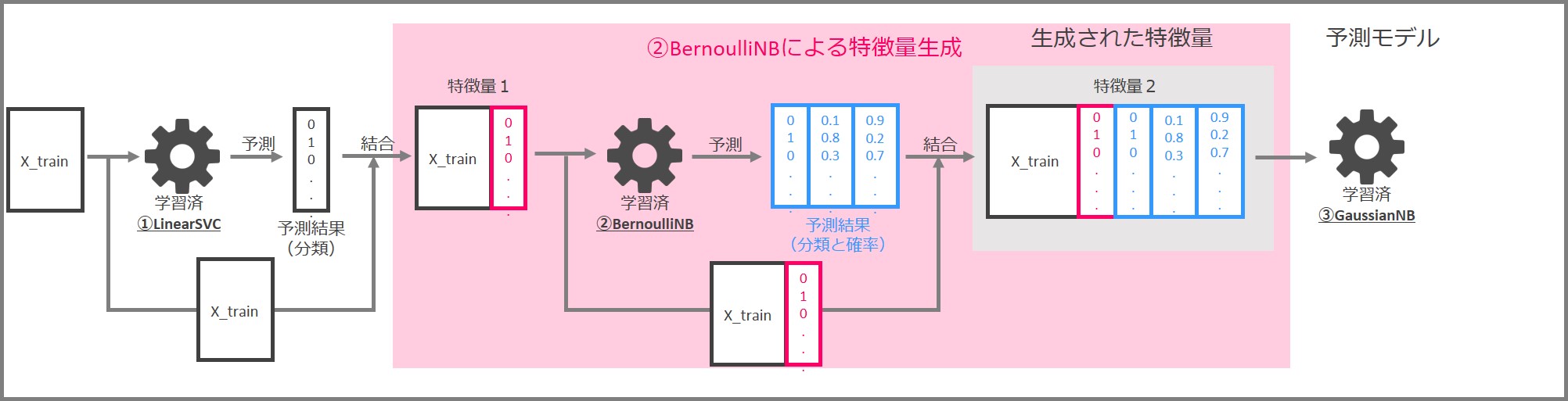
先ずはLinearSVCによる特徴量生成の部分です。
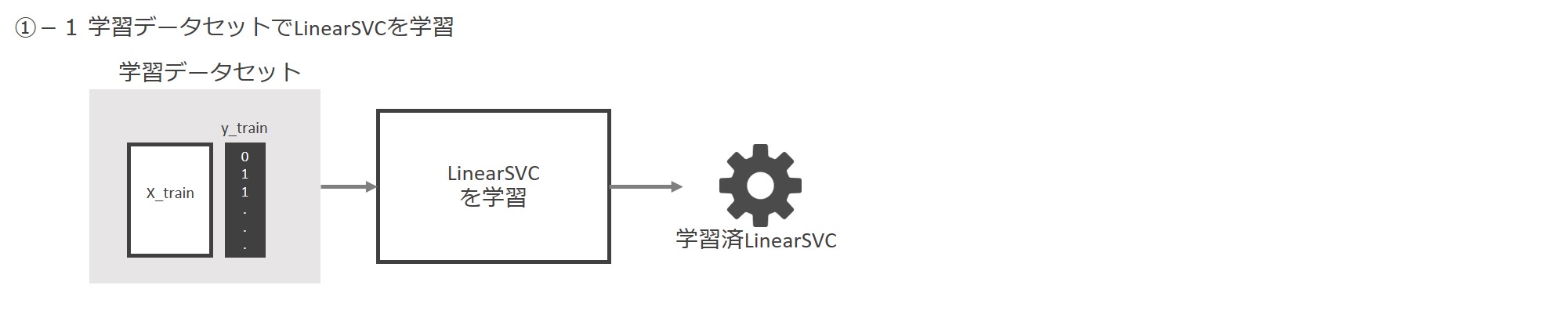
先ずは学習データセット「X_train」と「y_train」でLinearSVCを学習します。
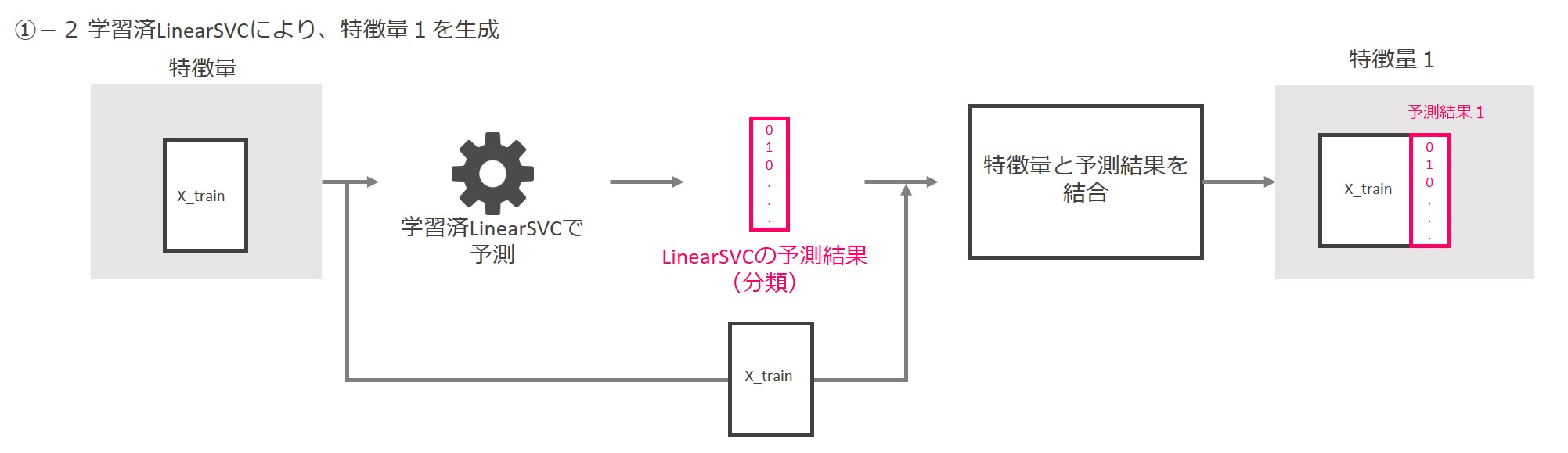
学習済LinearSVCに特徴量を入力し、0と1で構成される分類結果を出力します。入力した特徴量と予測結果を結合して、新しい特徴量(特徴量1)とします。
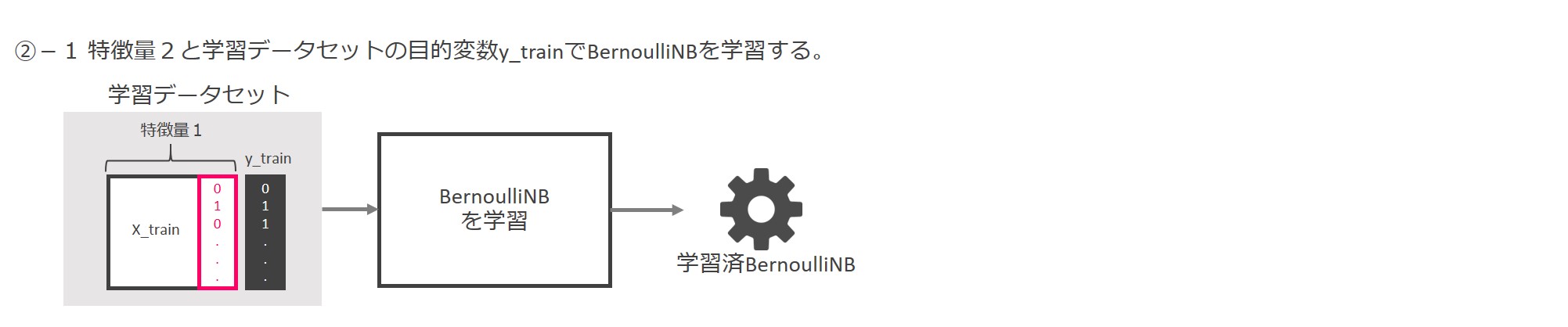
次はBernoulliNBによる特徴量生成です。
LinearSVCにより作られた「特徴量1」と「y_train」(学習データセットの目的変数)を使って、BernoulliNBを学習します。
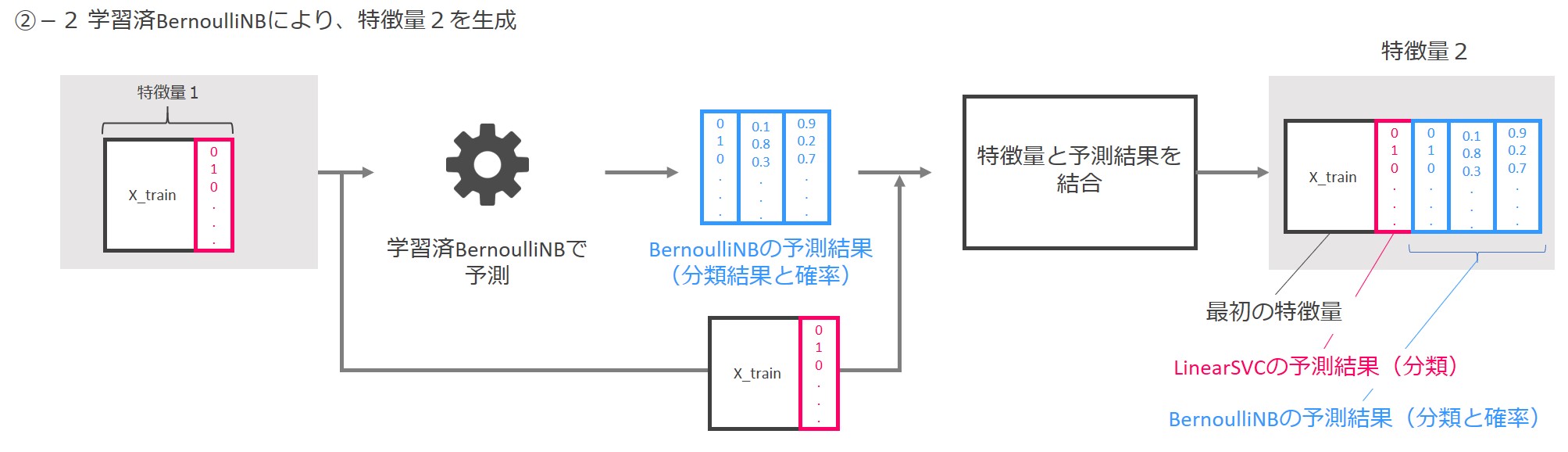
学習済BernoulliNBに「特徴量1」を入力し、予測結果を出力します。予測結果は「0と1からなる分類結果」と「0~1の間の数字からなるクラス(0 or 1)ごとの分類確率」です。「特徴量1」と予測結果を結合し、「特徴量2」を作成します。
今回は特徴量生成部がLinearSVCとBernoulliNBの2つから構成されますので、次の3つを結合したデータが最終的な特徴量となります。
- もとの特徴量「X_train」
- LinearSVCによる予測結果
- BernoulliNBによる予測結果
最後に予測モデル部です。
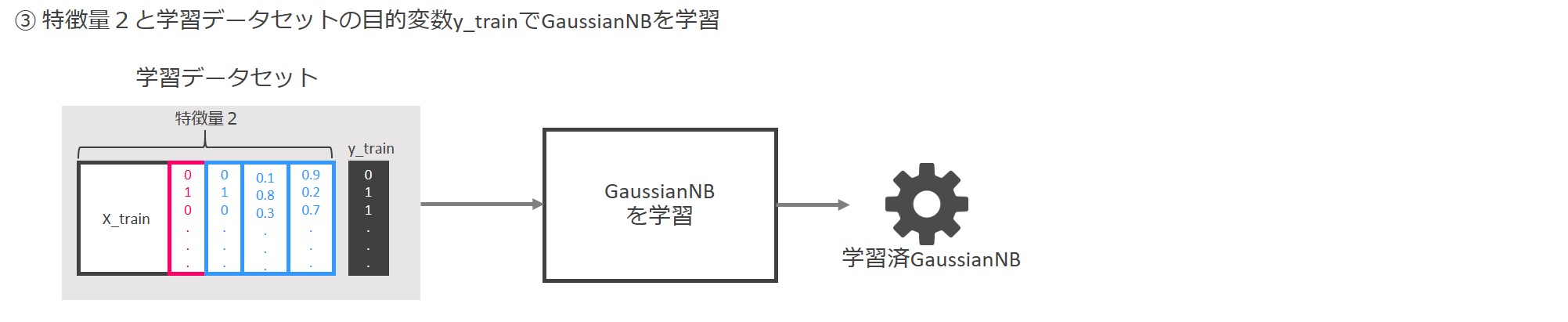
LinearSVCとBernoulliNBにより生成された「特徴量2」により、GaussianNBを学習します。
この学習済GaussianNBが予測モデルということになります。
まとめると、LinearSVCとBernoulliNBにより作成した特徴量を結合し、新しい特徴量を生成、その特徴量で予測モデル(GaussianNB)を生成するという流れになります。
学習済パイプラインを使った予測
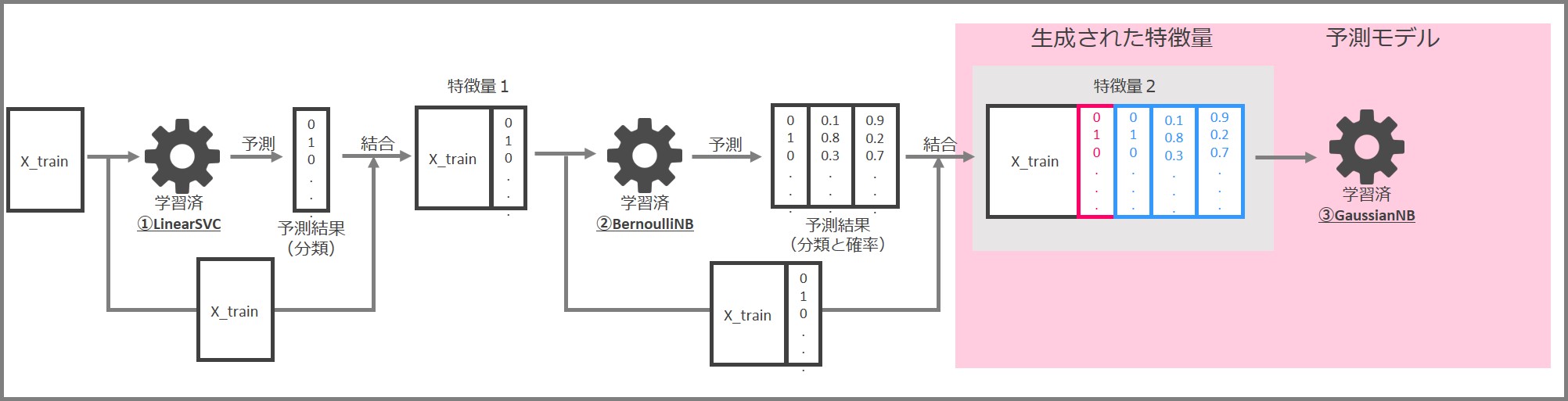
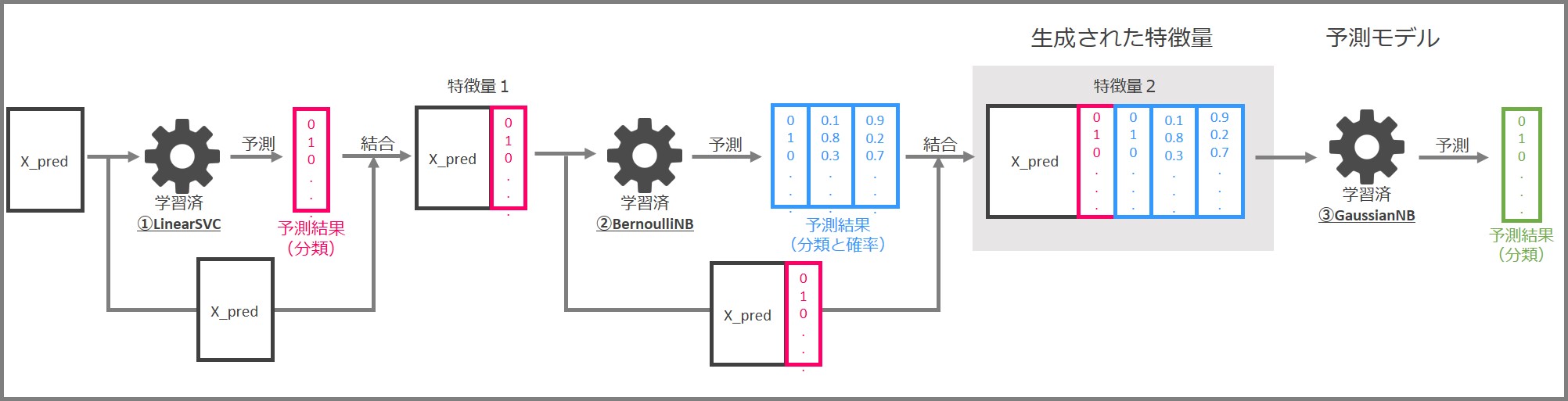
パイプラインでの予測の流れは次の通りです。
- 学習済パイプラインに予測用の特徴量X_predを入力する
- 学習済LinearSVCと学習済BernoulliNBから新たな特徴量を生成する
- 学習済GaussianNBで予測を実行する
詳しく見ていきます。
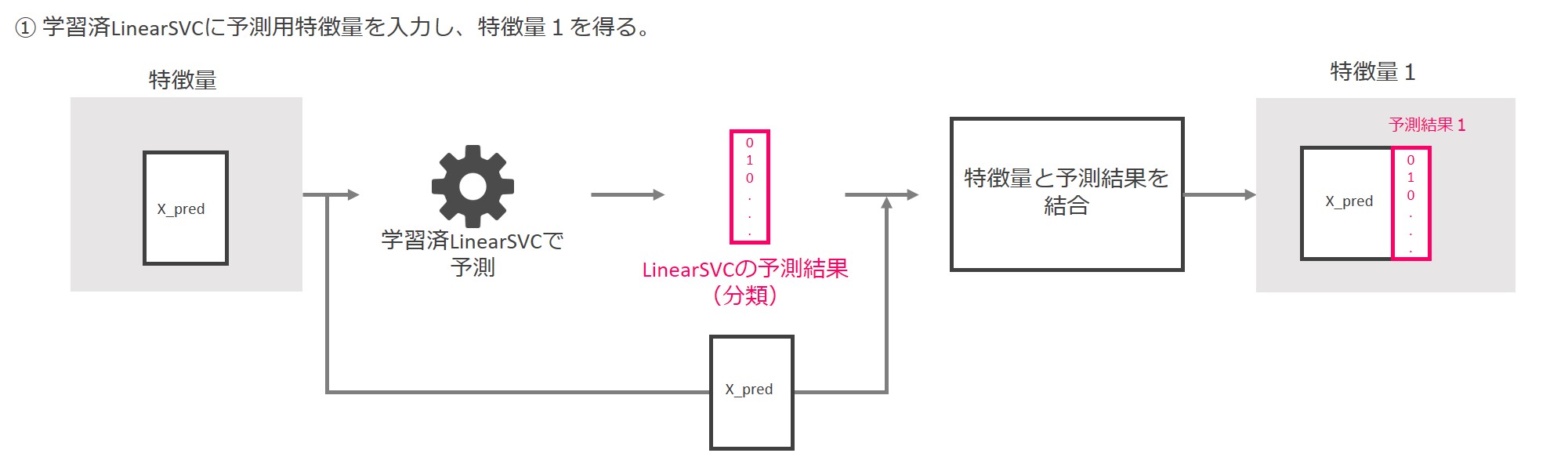
先ずは学習済のLinearSVCに予測用の特徴量X_predを入力し、0と1から成る予測結果を出力します。
その結果とX_predを結合し、「特徴量1」を得ます。
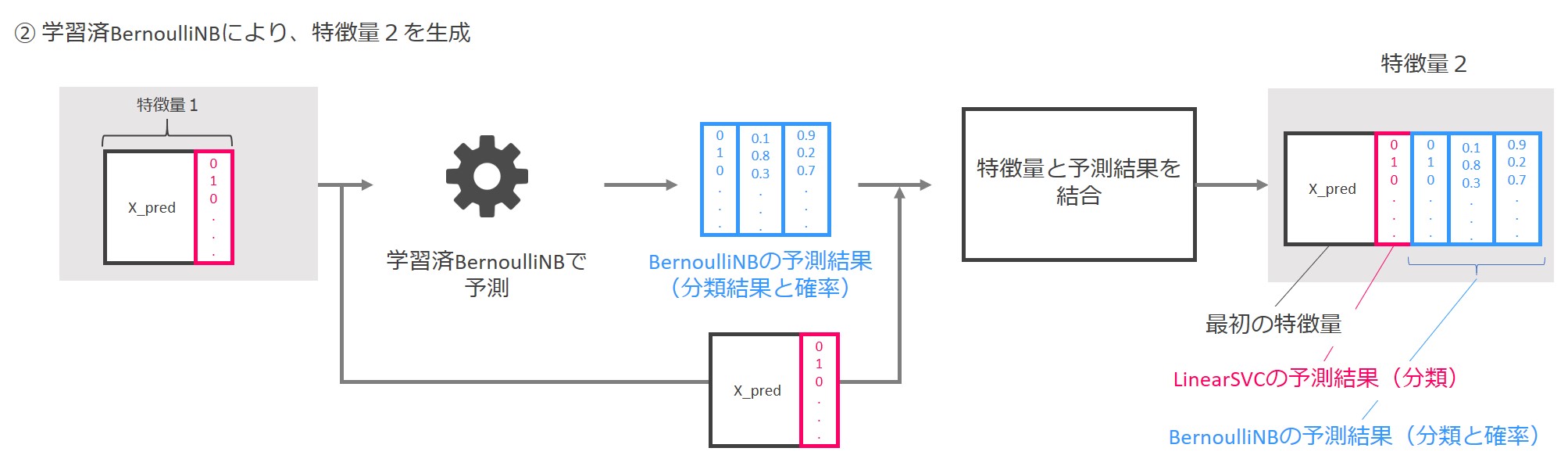
次に、「特徴量1」を学習済みBernoulliNBに入力し、0と1からなる分類の予測結果と、0と1に割り当てられる分類確率を出力します。
「特徴量1」に、0と1からなる分類の予測結果と、0と1に割り当てられる分類確率を結合し、「特徴量2」を生成します。
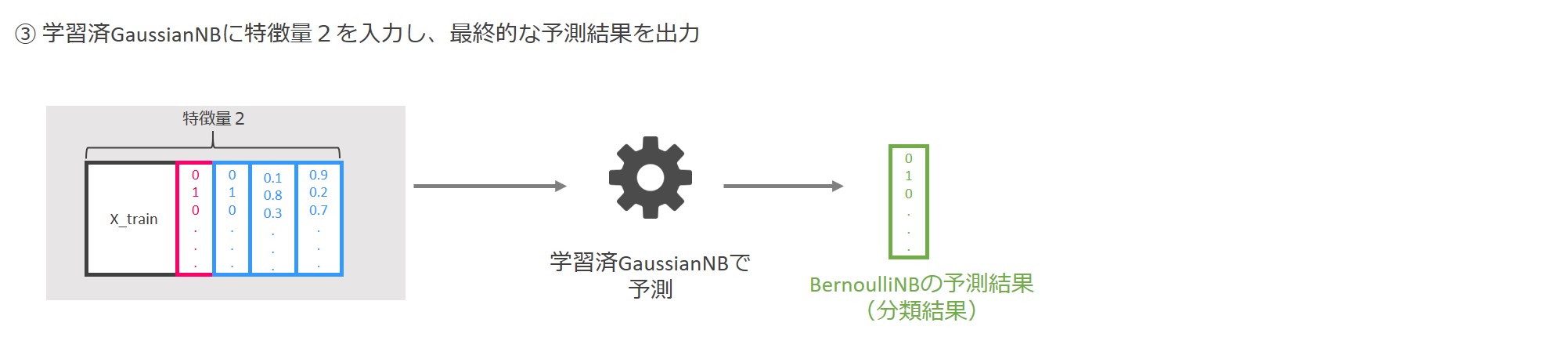
最後に学習済GaussianNBに「特徴量2」を入力し、0と1から成る最終的な予測結果を得ます。
このぐらい複雑になると、人知で思いつくのは、なかなか厳しいと思います。
なぜこのようなパイプラインが最適なのかを解釈することは、人の手で予測モデルを作るときや、データそのものの特徴を理解するときに、非常に有益です。
次回
次回は、TPOTとよく使われる機械学習モデルの「RandomForest」(ランダムフォレスト)との比較をしてみます。