今回はTPOTと代表的な機械学習アルゴリズムであるRandomForestとの比較をしてみます。
もう少し説明すると、AutoML(自動機械学習)を活用し自動で構築した数理モデル(パイプライン含む)と、データセットに対し直接RandomForestという数理モデルを構築した場合に、どの程度の予測精度の差が出るのかを見てみる、ということです。
ちなみに、RandomForestとはデータセットの一部を使って学習した小さな決定木を複数集め、その予測結果の平均を予測値とするアルゴリズムのことです。予測精度がそれなりに良いことから、数年前はよく使われていました。
今回は回帰問題を例に比較してみます。
Contents [hide]
利用するデータセット
データセットは第4回でも使ったカリフォルニアの住宅価格(https://scikit-learn.org/stable/datasets/index.html#california-housing-dataset)を使います。
例えば、カリフォルニアで家を購入しようとするときを考えます。ですが、住む予定での区画の相場が分かりません。相場がわからなければ事情があって安すぎる家を選んでしまったり、相場より高く家を買ってしまったりするかもしれません。
そこで、住む予定の区画の住宅価格の中央値を予測し、購入しようとしている住宅が相場どおりの価格かどうか確かめてみます。
今回も引き続きJupyterNotebookを使っていきます。
先ずは、カリフォルニアの住宅価格のデータセットを読み込みます。
以下、コードです。
from sklearn.datasets import fetch_california_housing california_housing = fetch_california_housing(as_frame=True) X = california_housing.data y = california_housing.target
予測を行う前に、カリフォルニアの住宅価格のデータセットの中身を確認しておきます。Xとyの中身を見てみましょう。
以下、Xの中身を見るためのコードです。
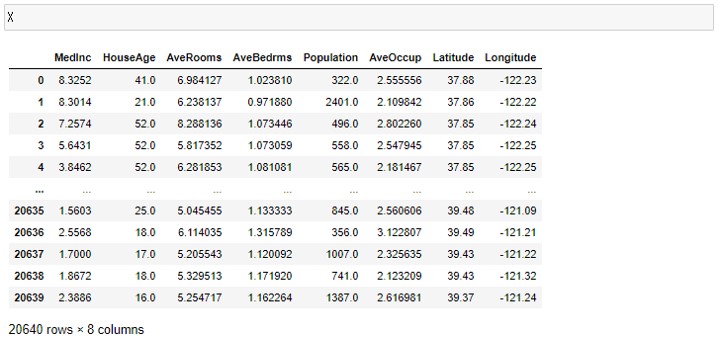
X
以下、実行結果です。
以下、yの中身を見るためのコードです。
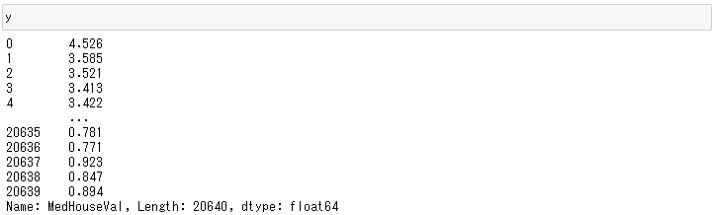
y
以下、実行結果です。
カリフォルニアの住宅価格データセットの目的変数である住宅価格は実際の価格ではなく最小値0.1499、最大値5.00001の間の値に変換されていることがわかります。
以下、yの最小値を見るためのコードです。
y.min()
以下、実行結果です。
以下、yの最大値を見るためのコードです。
y.max()
以下、実行結果です。
yの分布も見てみましょう。
以下、コードです。
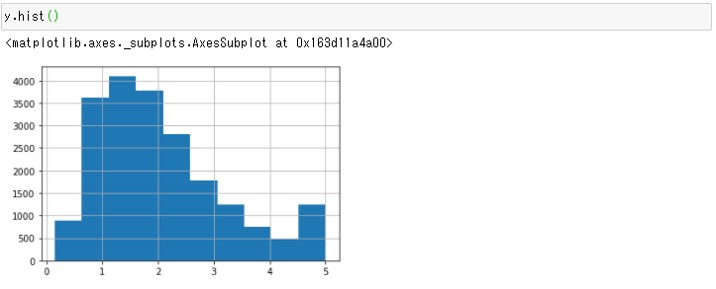
y.hist()
以下、実行結果です。
1.2あたりに山があり、5の付近に2つめの山があることがわかります。
5の付近の山が気になるので、詳細に見てみましょう。
yの属性sort_valuesでyの値を並べ替えることができます。ascending=Trueの場合は値を昇順で並べ替え、ascending=Falseの場合は値を降順で並べ替えます。
ここでは5の付近の値を知りたいので、降順(ascending=False)で並べ替えてみます。
以下、コードです。
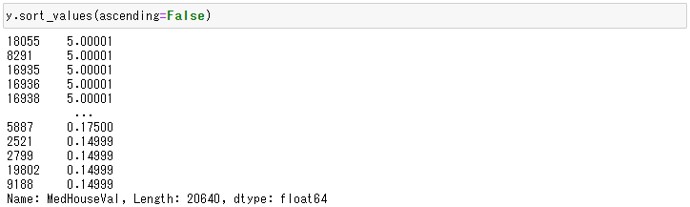
y.sort_values(ascending=False)
以下、実行結果です。
5.00001の値がしばらく並んでいます。
どれぐらいの数が5.00001になっているのか、確かめてみましょう。y[y==5.00001]で5.00001の値をもつyを抽出し、len関数でその数を数えます。
以下、コードです。
len(y[y==5.00001])
以下、実行結果です。
965件のyが5.00001の値であることがわかります。
ヒストグラムで5付近に山があるので、住宅価格が5で丸められている可能性が高いです。
実際の住宅価格をどのように変換しているのか、このデータセットの元論文を確認してみましたが、どのように変換しているのか記述はありませんでした。しかし、この5.00001はある値以上の住宅価格が丸められている可能性が高く、予測が困難そうだということが予想されます。
精度指標の選び方
RandomForestと比較するために、精度指標を選んでおきます。
以下の記号を使い精度指標の説明をします。
回帰問題の精度指標には次のように多数あります。
| 指標名 | 略称 | 説明 | TPOT実装 |
| 決定係数 | R2 | 目的変数の観測値に対する予測値の説明力を表す指標。1に近いほど良い予測である。 |
実装あり |
| Root Mean Squared Error | RMSE | 誤差(実測値と観測値の差)の二乗の平均のルートをとったもの。実測値と観測値の平均はほぼ0になってしまうので、いったん二乗とっている。0に近いほど実測値と予測値の値が近く、良い予測である。 |
なし |
| Mean Absolute Error | MAE | 誤差(実測値と観測値)の絶対値の平均。誤差をそのまま平均をとるとほぼ0になってしまうので、絶対値をとっている。0に近いほど実測値と予測値の値が近く、良い予測である。 |
実装あり |
| Mean Squared Error | MSE | 誤差(実測値と観測値の差)の二乗の平均。誤差の平均をとるとほぼ0になってしまうため、二乗している。 |
実装あり |
| Mean Absolute Percentage Error | MAPE | 実測値に対して、どれぐらいの誤差が含まれるのかを示す指標。値が0に近いほど実測値と予測値の値が近く、良い予測である。 |
実装あり |
外れ値のあるデータを予測するときにはMAE、そうでないデータを予測するときはRMSEが良いといわれています。今回のデータに外れ値はあるでしょうか。再びヒストグラムを見てみましょう。
ヒストグラムを見ると外れ値はないので、RMSEを使って学習しましょう。また相対的にどれぐらいの誤差があるか評価するためにMAPEも最後に計算しておきます。
予測するまでの流れ
予測するまでの流れです。
このうち、準備と学習データで学習するパートで、TPOTによる予測とRandomForestによる予測のコードが異なります。
それでは実際のコードの全体像です。
TPOTによる予測とRandomForestによる予測のコードは、以下の2か所で異なります。
- 「準備:精度指標の定義」の一部
- 「③学習用データで学習する」
あとはほとんど同じコードで予測することができます。これは、TPOTがscikit-learnの形式に合わせて開発されたからです。
TPOTとRandomForestのコードの比較
TPOTによる予測とRandomForestによる予測のコードを同時に見ながら、その違いを解説していきます。
準備:必要なライブラリの読み込み
先ずは、準備のうち必要なライブラリの読み込みです。
以下、TOPTによる予測のコードです。
from sklearn.datasets import fetch_california_housing from sklearn.model_selection import train_test_split from tpot import TPOTRegressor from sklearn.metrics import mean_squared_error from sklearn.metrics import make_scorer import matplotlib.pyplot as plt import numpy as np import time
以下、RandomForestによる予測のコードです。
from sklearn.datasets import fetch_california_housing from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestRegressor from sklearn.metrics import mean_squared_error import matplotlib.pyplot as plt import numpy as np import time
色付けした部分がTPOTとRandomForestで異なります。
読み込んだモジュールは次のとおりです。TPOTによる予測とRandomForestによる予測に共通するモジュールと、それぞれに独自のモジュールがあります。
共通のモジュール:
- fetch_california_housing … カリフォルニアの住宅価格のデータセット
- train_test_split … データセットを分割するモジュール
- mean_squared_error … 精度指標MeanSquaredErrorを計算するモジュール
- pyplot … 予測結果をプロットするモジュール
- numpy … 各種数学計算をするモジュール
- time … 時間を計測するモジュール
TPOTによる予測でのみ使うモジュール:
- TPOTRegressor … TPOTで回帰問題を学習・予測するモジュール
- make_scorer … TPOTのパイプラインへユーザーが定義した評価指標を渡すためのモジュール
RandomForestによる予測でのみ使うモジュール:
- RandomForestRegressor … RandomForestで回帰問題を学習・予測するモジュール
準備:精度指標の定義
次に、今回使う精度指標RMSEとMAPEを定義しておきます。
この2つの指標は、scikit-learnに実装されていないので、自分で関数を作っておく必要があります。
ここで、RMSEをTPOTのパイプラインに渡すためにmake_scorer関数を使います。greater_is_betterパラメータがTrueなら定義した精度指標の値が高ければよい予測であることを示し、Falseなら値が低ければよい予測であることを示します。RMSEは値が小さいほうが良い予測なので、Falseとしておきます。
以下、TOPTによる予測のコードです。
# MAPEを計算する関数を定義する
def mape(y_test, y_pred):
return np.sum(np.abs((y_test - y_pred) / y_test))/len(y_test)
# RMSEを計算する関数を定義する
def my_custom_rmse(y_true, y_pred):
return np.sqrt(mean_squared_error(y_true=y_true,y_pred=y_pred))
my_custom_scorer = make_scorer(my_custom_rmse, greater_is_better=False)
以下、RandomForestによる予測のコードです。
# MAPEを計算する関数を定義する
def mape(y_test, y_pred):
return np.sum(np.abs((y_test - y_pred)/ y_test))/len(y_test)
# RMSEを計算する関数を定義する
def my_custom_rmse(y_true, y_pred):
return np.sqrt(mean_squared_error(y_true=y_true,y_pred=y_pred))
準備:開始時間の定義
次に、TPOTによる予測とRandomForestによる予測の実行時間を比較をしたいので、プログラムの開始時間を定義しておきます。
定義と言っても、現在時刻を取得し、それをプログラムの開始時間として定義します。
timeモジュールのtime関数で現在時刻を取得することができます。これはTPOTによる予測とRandomForestによる予測で共通です。
以下、コード(TPOTによる予測とRandomForestによる予測で共通)です。
start = time.time()
準備はここまでです、いよいよ予測をはじめます。
①データセットの読み込み
カリフォルニアの住宅価格のデータセットを読み込み、特徴量をXに、目的変数をyに格納します。
ここのコードは、TPOTによる予測とRandomForestによる予測で共通です。
どのようなデータが格納されているかは、前段の「利用するデータセット」セクションをご覧ください。また、データの詳しい説明は第4回「AutoML【TPOT】で回帰問題を解く」をご覧ください。
以下、コード(TPOTによる予測とRandomForestによる予測で共通)です。
# データセットをXとyに読み込む california_housing = fetch_california_housing(as_frame=True) X = california_housing.data y = california_housing.target print(np.shape(X)) # Xのデータの行数と列数 print(np.shape(y)) # yのデータの行数と列数
②データセットを学習用と検証用に分割する
こちらもTPOTによる予測とRandomForestによる予測で共通です。
train_test_split関数でデータセットを分割します。test_sizeパラメータで検証用のデータをどれぐらいの割合で使うか指定します。デフォルトでは乱数を使ってデータセットをランダムに学習用と検証用に振り分けます。
print文でXとyがそれぞれどのように分割されたか確認しています。random_stateに数値を指定しておくことで、実行するたびに同じ分割結果を得ることができます。
以下、コード(TPOTによる予測とRandomForestによる予測で共通)です。
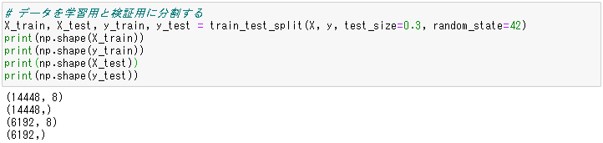
# データを学習用と検証用に分割する X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) print(np.shape(X_train)) print(np.shape(y_train)) print(np.shape(X_test)) print(np.shape(y_test))
以下、実行結果です。
X_trainとy_trainは14448行、X_testとy_testは6192行で、6192(検証データの数)÷20640(元の行数)=0.3となり、学習用:検証用=7:3と分割されたことがわかります。
③学習用データで学習する
TPOTによる予測とRandomForestによる予測で、コードが異なります。
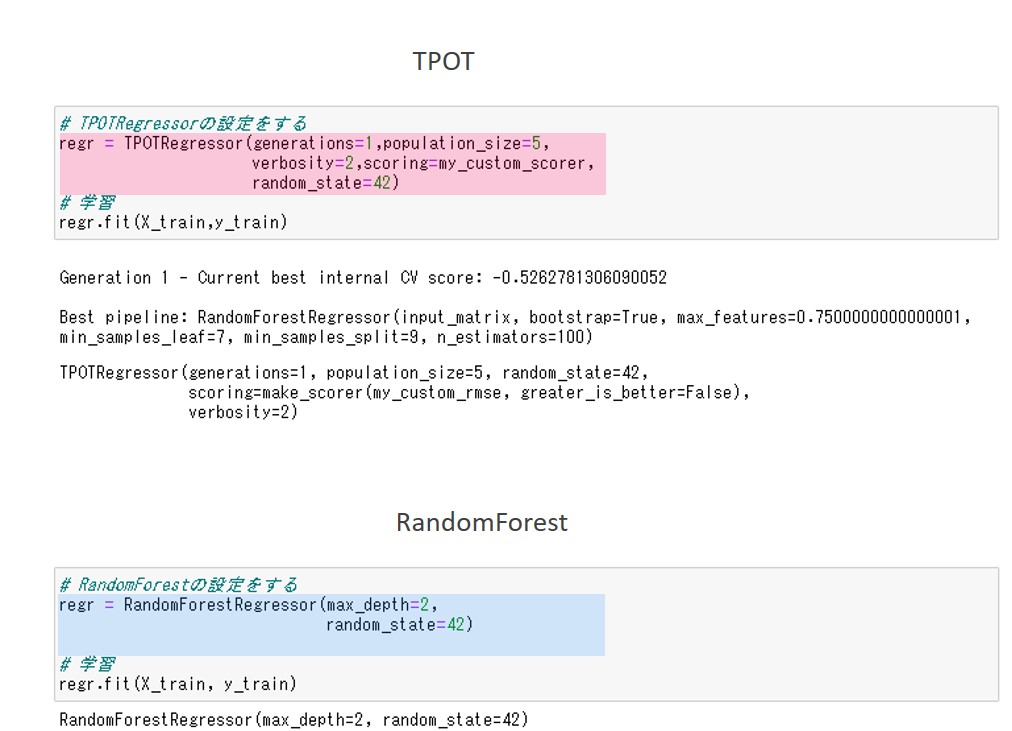
以下、TOPTによる予測のコードです。
# TPOTRegressorの設定をする
regr = TPOTRegressor(generations=1,population_size=5,
verbosity=2,scoring=my_custom_scorer,
random_state=42)
# 学習
regr.fit(X_train,y_train)
- generations … 特徴量の最適化とパラメータチューニングの最適化を何回繰り返すかを指定します。
- population_size … TPOTが使っている遺伝的アルゴリズム内のパラメータです。
- verbosity … 進捗状況を表示させるためのもので、プログレスバーを表示させる場合には2を設定します。
- scoring … TPOTパイプラインの最適化使う精度指標を指定します。ここでは、準備で定義したRMSEをTPOTに渡せるように関数化したmy_custom_scorerを使います。
- random_state … 再度実行しても同じ結果が得られるよう、42を指定しておきます。実行のたびに結果が変わっても良い場合は、指定しなくても良いです。
以下、RandomForestによる予測のコードです。
# RandomForestの設定をする
regr = RandomForestRegressor(max_depth=2,
random_state=42)
regr.fit(X_train, y_train)
# 学習
regr.fit(X_train, y_train)
- max_depth … 決定木の深さを指定します。
- random_state … 再度実行しても同じ結果が得られるよう、42を指定しておきます。実行のたびに結果が変わっても良い場合は、指定しなくても良いです。
以下、実行結果です。
TPOTによる予測もRandomForestによる予測も、共通してそれぞれの設定内容が出力されています。
TPOTによる予測の方では、さらに最適化されたパイプラインも出力されています。TPOTによる予測の最適化されたパイプラインを見ると、予測器はRandomForestになっています。
RandomForestによる予測の結果と比べると、パラメータの値が異なっていることがわかります。
④検証用データで予測する
TPOTによる予測とRandomForestによる予測のコードは同一です。
以下、コード(TPOTによる予測とRandomForestによる予測で共通)です。
# 検証用データで予測 y_pred = regr.predict(X_test)
興味のある方は、print(y_pred)で予測結果を確認してみてください。両者で異なっていることがわかります。あとでどちらが良い予測をしているか確認します。
⑤精度指標を計算する
冒頭で定義したMAPEとRMSEの関数を使って、計算します。TPOTによる予測とRandomForestによる予測のコードは同一です。
以下、コード(TPOTによる予測とRandomForestによる予測で共通)です。
# 精度指標のRMSEとMAPEを計算する
RMSE = my_custom_rmse(y_true=y_test, y_pred=y_pred)
MAPE = mape(y_test=y_test, y_pred=y_pred)
# 精度指標の計算結果を出力する
print('RMSE=' + str(RMSE))
print('MAPE=' + str(MAPE))
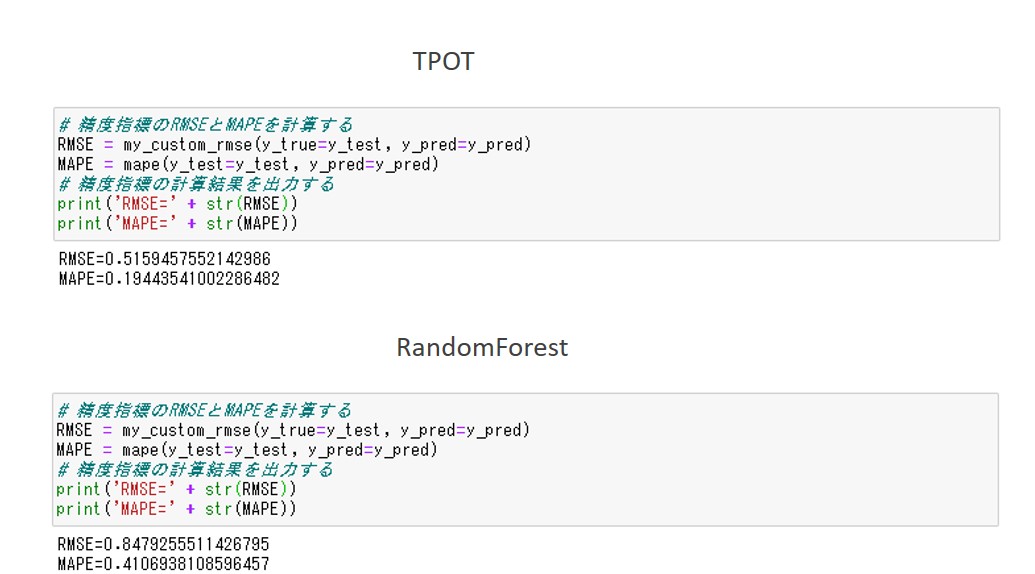
以下、実行結果です。
TPOTによる予測:
- RMSEは、0.52
- MAPEは、0.19
RandomForestによる予測:
- RMSEは、0.85
- MAPEは、0.41
RMSEもMAPEも値が小さいほうが良い予測なので、TPOTによる予測のほうが良いことがわかります。
確認:結果のプロット
精度指標だけではどの程度良い予測ができたのかわからないので、正解データ(y_test)と予測データ(y_pred)を散布図にプロットしてみます。TPOTによる予測とRandomForestによる予測のコードは同一です。
以下、コード(TPOTによる予測とRandomForestによる予測で共通)です。
# プロット
plt.figure(figsize=(5,5)) # 図のサイズが正方形になるように設定
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('y_test')
plt.ylabel('y_pred')
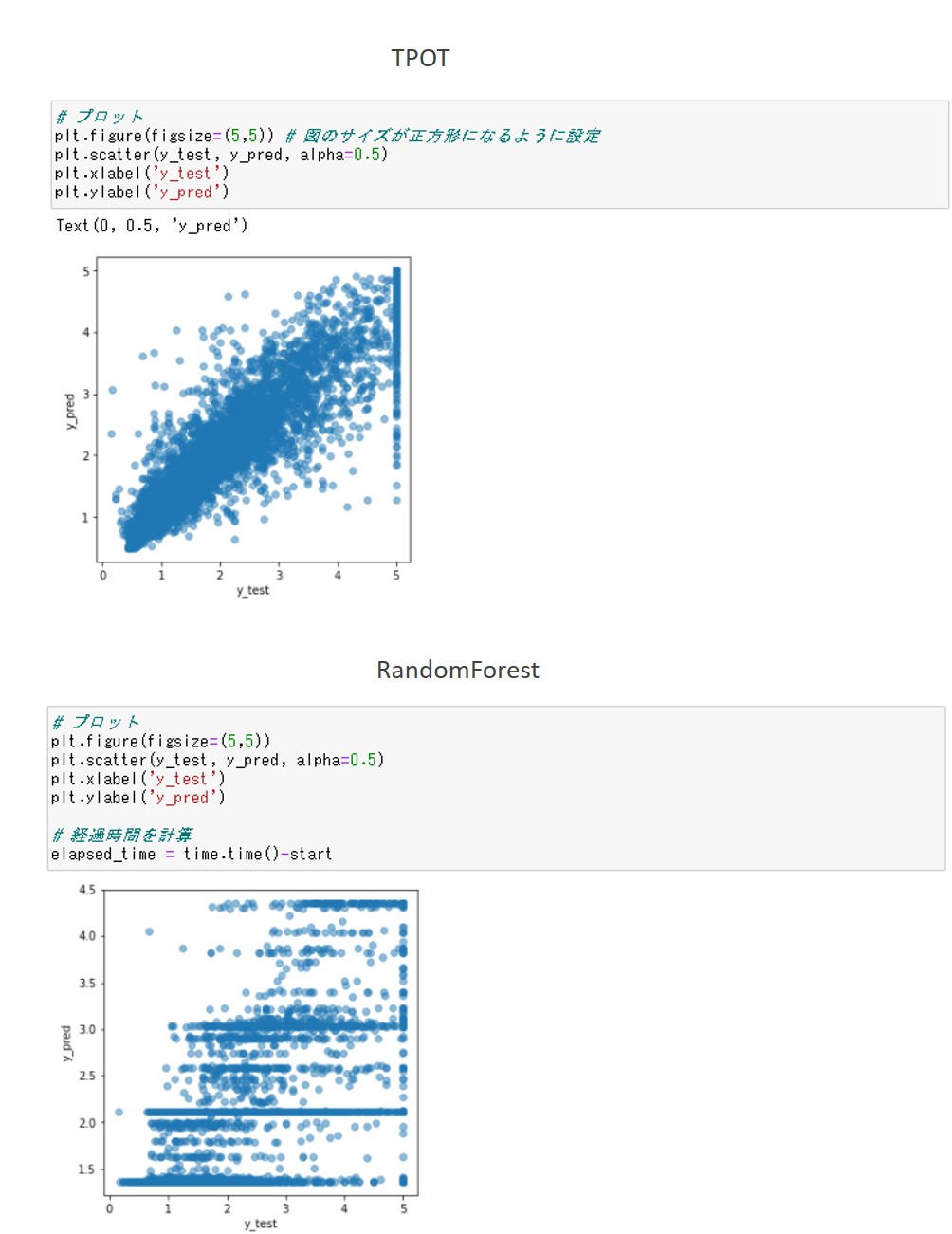
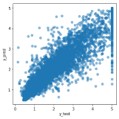
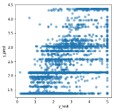
以下、実行結果です。
TPOTによる予測の方が、y_test=y_predの線上にプロットが集中しており、良い予測ができていることがわかります。
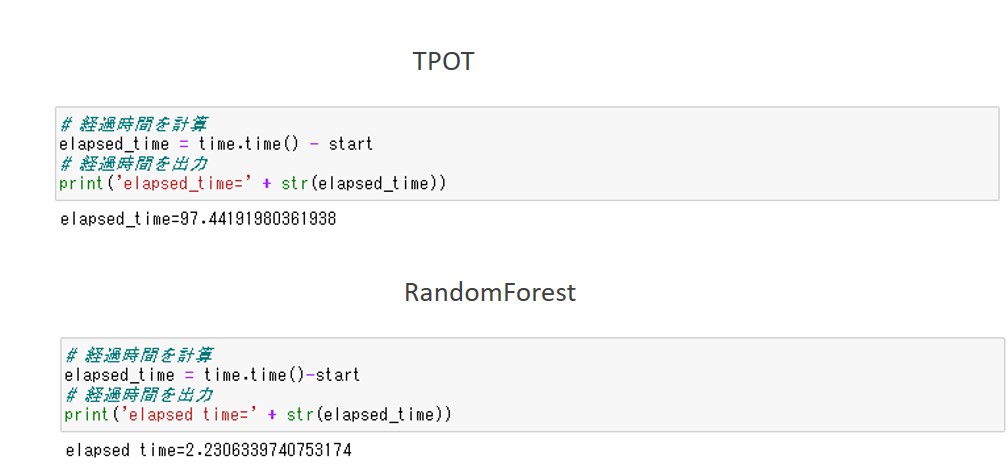
確認:経過時間の計算と出力
最後に経過時間を出力します。TPOTによる予測とRandomForestによる予測のコードは同一です。
以下、コード(TPOTによる予測とRandomForestによる予測で共通)です。
# 経過時間を計算
elapsed_time = time.time() - start
# 経過時間を出力
print('elapsed_time=' + str(elapsed_time))
以下、実行結果です。
TPOTによる予測は約97秒、RandomForestによる予測は約2秒実行に時間がかかります。
RandomForestによる予測の方が圧倒的に速いことがわかります。
TPOTによる予測のコードの全体像
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from tpot import TPOTRegressor
from sklearn.metrics import mean_squared_error
from sklearn.metrics import make_scorer
import matplotlib.pyplot as plt
import numpy as np
import time
# MAPEを計算する関数を定義する
def mape(y_test, y_pred):
return np.sum(np.abs((y_test - y_pred) / y_test))/len(y_test)
# RMSEを計算する関数を定義する
def my_custom_rmse(y_true, y_pred):
return np.sqrt(mean_squared_error(y_true=y_true,y_pred=y_pred))
my_custom_scorer = make_scorer(my_custom_rmse, greater_is_better=False)
start = time.time()
print(start)
# データセットをXとyに読み込む
california_housing = fetch_california_housing(as_frame=True)
X = california_housing.data
y = california_housing.target
print(np.shape(X))
print(np.shape(y))
# データを学習用と検証用に分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
print(np.shape(X_train))
print(np.shape(y_train))
print(np.shape(X_test))
print(np.shape(y_test))
# TPOTRegressorの設定をする
regr = TPOTRegressor(generations=1,population_size=5,
verbosity=2,scoring=my_custom_scorer,
random_state=42)
# 学習
regr.fit(X_train,y_train)
# 検証用データで予測
y_pred = regr.predict(X_test)
# 予測結果を表示
print(y_pred)
# 精度指標のRMSEとMAPEを計算する
RMSE = my_custom_rmse(y_true=y_test, y_pred=y_pred)
MAPE = mape(y_test=y_test, y_pred=y_pred)
# 精度指標の計算結果を出力する
print('RMSE=' + str(RMSE))
print('MAPE=' + str(MAPE))
# プロット
plt.figure(figsize=(5,5)) # 図のサイズが正方形になるように設定
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('y_test')
plt.ylabel('y_pred')
# 経過時間を計算
elapsed_time = time.time() - start
# 経過時間を出力
print('elapsed_time=' + str(elapsed_time))
RandomForestによる予測のコードの全体像
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
import numpy as np
import time
# MAPEを計算する関数を定義する
def mape(y_test, y_pred):
return np.sum(np.abs((y_test - y_pred)/ y_test))/len(y_test)
# RMSEを計算する関数を定義する
def my_custom_rmse(y_true, y_pred):
return np.sqrt(mean_squared_error(y_true=y_true,y_pred=y_pred))
start = time.time()
print(start)
# データセットをXとyに読み込む
california_housing = fetch_california_housing(as_frame=True)
X = california_housing.data
y = california_housing.target
print(np.shape(X))
print(np.shape(y))
# データを学習用と検証用に分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
print(np.shape(X_train))
print(np.shape(y_train))
print(np.shape(X_test))
print(np.shape(y_test))
# RandomForestRegressorの設定をする
regr = RandomForestRegressor(max_depth=2,
random_state=42)
# 学習
regr.fit(X_train, y_train)
# 検証用データで予測
y_pred = regr.predict(X_test)
# 予測結果を表示
print(y_pred)
# 精度指標のRMSEとMAPEを計算する
RMSE = my_custom_rmse(y_true=y_test, y_pred=y_pred)
MAPE = mape(y_test=y_test, y_pred=y_pred)
# 精度指標の計算結果を出力する
print('RMSE=' + str(RMSE))
print('MAPE=' + str(MAPE))
# プロット
plt.figure(figsize=(5,5)) # 図のサイズが正方形になるように設定
plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel('y_test')
plt.ylabel('y_pred')
# 経過時間を計算
elapsed_time = time.time() - start
# 経過時間を出力
print('elapsed_time=' + str(elapsed_time))
比較一覧
| 指標 | TPOT | Random Forest |
| コードの量
※少ないほうが良い |
39行
※コメント行を除く |
○38行
※コメント行を除く |
| 精度(RMSE)
※小さいほうが良い |
○0.52 | 0.85 |
| 精度(MAPE) | ○0.19 | 0.41 |
| 実行時間
※短いほうが良い |
97秒 | ○2秒 |
コードの量と実行時間はRandomForestによる予測に軍配が上がりましたが、RMSEとyyプロット(散布図)を見ると精度はTPOTによる予測の方がはるかに良いことがわかります。
MAPEを見ると、実測値に対して、TPOTによる予測では19%の誤差、RandomForestによる予測では41%の誤差があることがわかります。
この結果を見て、TPOTとRandomForestのどちらを選ぶかは予測の目的によりますが、今回は1分半程度で2倍の予測精度を出すTPOTによる予測の方が良さそうです。
ちなみにyyプロットとは、横軸に検証データの目的変数(y_test)、縦軸に検証データに対する予測値(y_pred)をプロットした図です。y_test=y_predとなる線上の近くに点が集まっていれば良い予測といえます。
次回
次回は、TPOTのパイプラインに使われる変換器(特徴量の自動生成と予測モデル)の一覧とその説明をします。