Rでサクッと時系列データの変化点を見つける方法

14137
Rでサクッと時系列データの変化点を見つける方法

ビジネスの世界のデータの多くは、時間軸のあるデータである時系列データです。

この時系列データは、一定ではありません。上昇トレンドがあったかと思えば、下降トレンドになったりします。

要は、構造変化します。

時系列データを手に入れたら、どのようなデータかなんとなく知りたくなります。その1つが構造が変化する時期（変化点）です。

この構造変化を検出する技術は色々とあります。

幸いにも、Rのライブラリーの中に時系列データの構造変化を見つけるためのパッケージがいくつかあります。

今回は、「Rでサクッと時系列データの変化点を見つける方法」というお話しをします。

構造変化の種類

今回扱う構造変化とは、目的変数Yが1変量の場合のパラメータ（切片や係数など）が変化することを指しています。

主に3点です。

  • 水準変化
  • トレンド変化
  • 分散変化

他にも色々あると思いますが、今回はこの3点を扱います。

出来る限り理論的なお話しは避けていきます。深掘りすると、ややこしいお話しがてんこ盛りの世界です。

パッケージ

今回は、次のライブラリーを使います。

以下を参考に、まだインストールしていない方は、インストールして頂ければと思います。

# パッケージのインストール
install.packages('strucchange', dependencies = TRUE)

 

strucchangeは、主に水準変化やトレンド変化の検知に使えます。

一様、Generalized M-Fluctuation Tests（日本語でどのように訳されているのか知りません……）などと絡めたり、残差を中心化し2乗したり、何かしら工夫すれば分散変化の検知もできます。このあたりは少しややこしく分かりにくくなりますので、残差を中心化し2乗する簡易的な方法のみ説明します。

データセット

以下の4点のデータセットを使います。

  • データセット①：ECサイトの購買件数（水準変化・トレンド変化）　Purchases
  • データセット②：ナイル川の年間流量（水準変化）　Nile
  • データセット③：生産センサーデータ１（水準変化）　Sensor1
  • データセット④：生産センサーデータ２（分散変化）　Sensor2

データセット②は、最初からRのサンプルデータとして提供されているデータセットのため、直ぐに利用できます。

残りの3つのデータセットは、読み込む必要があります。弊社のHPのURL（https://www.salesanalytics.co.jp/）からダウンロードできます。

以下、データセットを読み込み時系列型（ts）にするコードです。

# データセット①：ECサイトの購買件数（水準変化・トレンド変化）　Purchases
url <- "https://www.salesanalytics.co.jp/yyc1"
table <- read.csv(url)
Purchases <- ts(table$Purchases)

# データセット③：生産センサーデータ１（水準変化）　Sensor1
url <- "https://www.salesanalytics.co.jp/wxoh"
table <- read.csv(url, header = FALSE, col.names="Sensor1")
Sensor1 <- ts(table$Sensor1)

# データセット④：生産センサーデータ２（分散変化）　Sensor2
url <- "https://www.salesanalytics.co.jp/0bax"
table <- read.csv(url, header = FALSE, col.names="Sensor2")
Sensor2 <- ts(table$Sensor2)

 

データの確認

それぞれのデータセットをグラフ化し、確認していきたいと思います。

データセット①「ECサイトの購買件数」のグラフ化

以下、コードです。

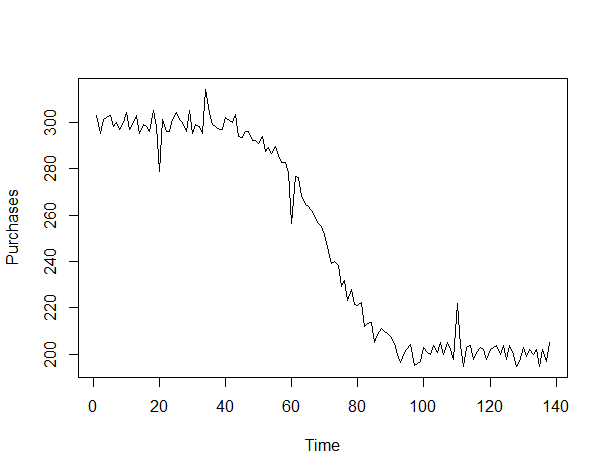
plot(Purchases)

 

以下、実行結果です。

 

水準変化とトレンド変化が起きていることが分かります。

データセット②「ナイル川の年間流量」のグラフ化

以下、コードです。

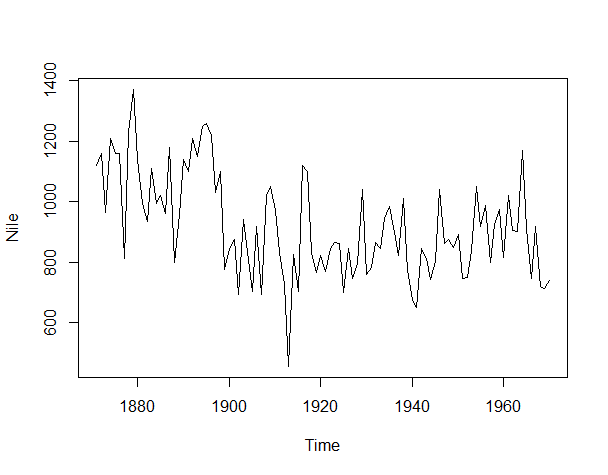
plot(Nile)

 

以下、実行結果です。

 

水準変化が起きていることが分かります。

データセット③「生産センサーデータ１」のグラフ化

以下、コードです。

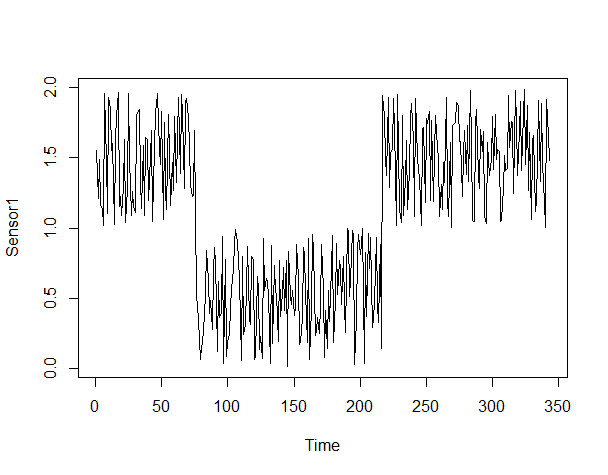
plot(Sensor1)

 

以下、実行結果です。

 

水準変化が起きていることが分かります。

データセット④「生産センサーデータ２」のグラフ化

以下、コードです。

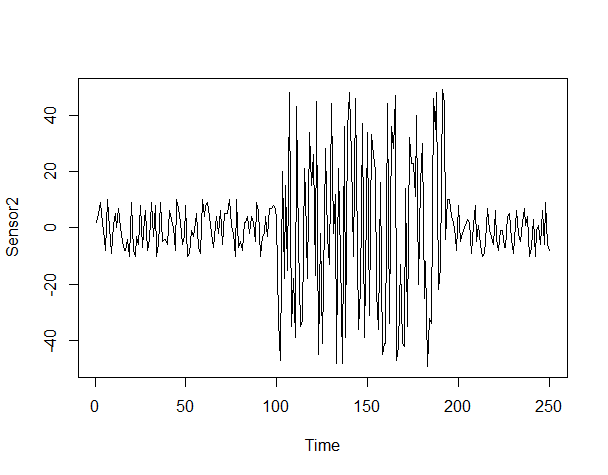
plot(Sensor2)

 

以下、実行結果です。

 

分散変化が起きていることが分かります。

 

変化点検知

今回利用するライブラリーをロード（読み込み）します。

以下、コードです。

# ライブラリーの読み込み
library(strucchange)

 

データセット①「ECサイトの購買件数」の変化点検知

対象データを、ts_dataに代入し変化点検知を実施していきます。

以下、コードです。

# 対象データの代入
ts_data <- Purchases

 

変化点検知をします。

以下、コードです。

# 実行
lin.trend <- 1:length(ts_data)            #トレンド変数
bp_ts <- breakpoints(ts_data ~ lin.trend) #変化点推定

 

実行結果を確認します。

以下、コードです。

# 結果の確認
plot(bp_ts)
summary(bp_ts)

 

以下、実行結果です。

 

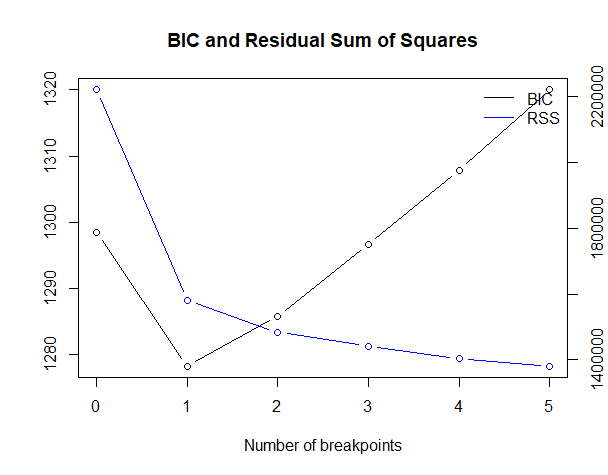
RSS（残差平方和、Residual sum of squares）とBIC（ベイズ情報量規準、Bayesian information criterion）は、どちらの数値も小さい方が良いとされています。

BICが最も小さいケースを最適としています。

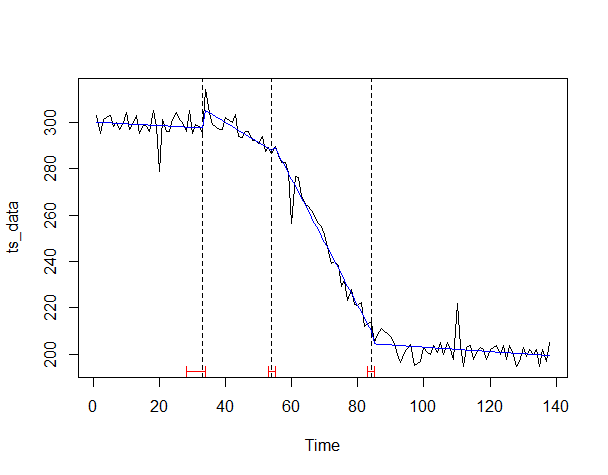
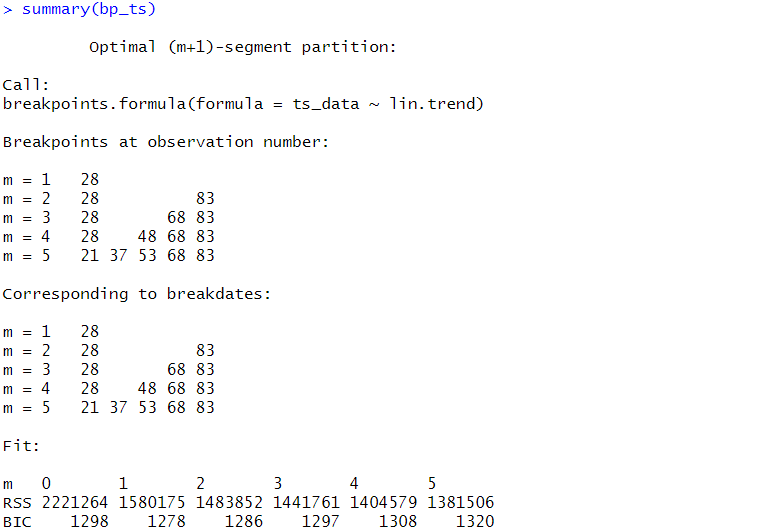
今回のケースでは、変化点が3が最適になっています。

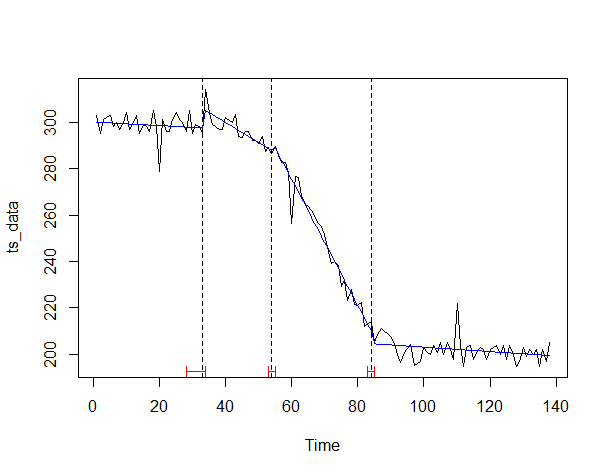
変化点が3つの場合、以下となります。

  • 33
  • 54
  • 84

3つの変化点で分割すると、データは4区分になります。区分ごとの回帰線を推定します。

以下、コードです。

# 回帰線の推定
coefficients(bp_ts)                                  #切片と係数
fm <- lm(ts_data ~ breakfactor(bp_ts)/(lin.trend)-1) #推定値

 

以下、実行結果です。

 

グラフで視覚的に確認したいと思います。

以下、コードです。

# プロット
ci_ts <- confint(bp_ts)        #変化点の信頼区間 
plot(ts_data)                  #対象データの描写（折れ線）
lines(bp_ts)                   #変化点の描写（縦線）
lines(ci_ts)                   #信頼区間の描写（赤）
lines(ts(fitted(fm)), col = 4) #回帰線の描写（青）

 

以下、実行結果です。

 

水準変化とトレンド変化を捉え、何となく感覚的に合致するかと思います。

最後に、オブジェクトを削除します。

# オブジェクトの削除
rm(bp_ts)
rm(ci_ts)

 

データセット②「ナイル川の年間流量」の変化点検知

対象データを、ts_dataに代入し変化点検知を実施していきます。

以下、コードです。

# 対象データの代入
ts_data <- ts(Nile)

 

変化点検知をします。

以下、コードです。

# 実行
lin.trend <- 1:length(ts_data)            #トレンド変数
bp_ts <- breakpoints(ts_data ~ lin.trend) #変化点推定

 

実行結果を確認します。

以下、コードです。

# 結果の確認
plot(bp_ts)
summary(bp_ts)

 

以下、実行結果です。

 

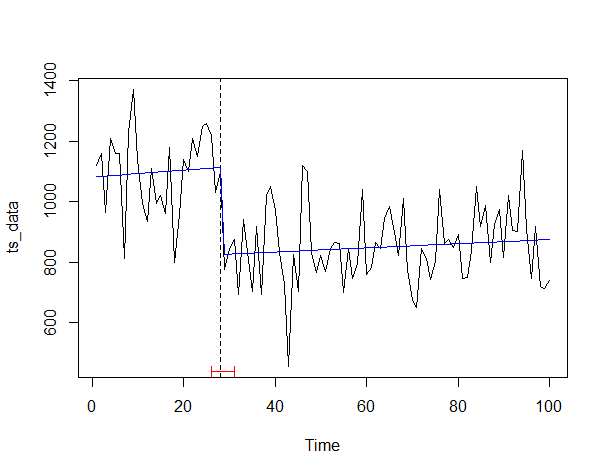
今回のケースでは、変化点が1が最適になっています。

変化点が1つの場合、以下となります。

  • 28

1つの変化点で分割すると、データは2区分になります。区分ごとの回帰線を推定します。

以下、コードです。

# 回帰線の推定
coefficients(bp_ts)                                  #切片と係数
fm <- lm(ts_data ~ breakfactor(bp_ts)/(lin.trend)-1) #推定値

 

以下、実行結果です。

 

グラフで視覚的に確認したいと思います。

以下、コードです。

# プロット
ci_ts <- confint(bp_ts)        #変化点の信頼区間 
plot(ts_data)                  #対象データの描写（折れ線）
lines(bp_ts)                   #変化点の描写（縦線）
lines(ci_ts)                   #信頼区間の描写（赤）
lines(ts(fitted(fm)), col = 4) #回帰線の描写（青）

 

以下、実行結果です。

 

水準変化を捉え、何となく感覚的に合致するかと思います。

最後に、オブジェクトを削除します。

# オブジェクトの削除
rm(bp_ts)
rm(ci_ts)

 

データセット③「生産センサーデータ１」の変化点検知

対象データを、ts_dataに代入し変化点検知を実施していきます。

以下、コードです。

# 対象データの代入
ts_data <- Sensor1

 

変化点検知をします。

以下、コードです。

# 実行
lin.trend <- 1:length(ts_data)            #トレンド変数
bp_ts <- breakpoints(ts_data ~ lin.trend) #変化点推定

 

実行結果を確認します。

以下、コードです。

# 結果の確認
plot(bp_ts)
summary(bp_ts)

 

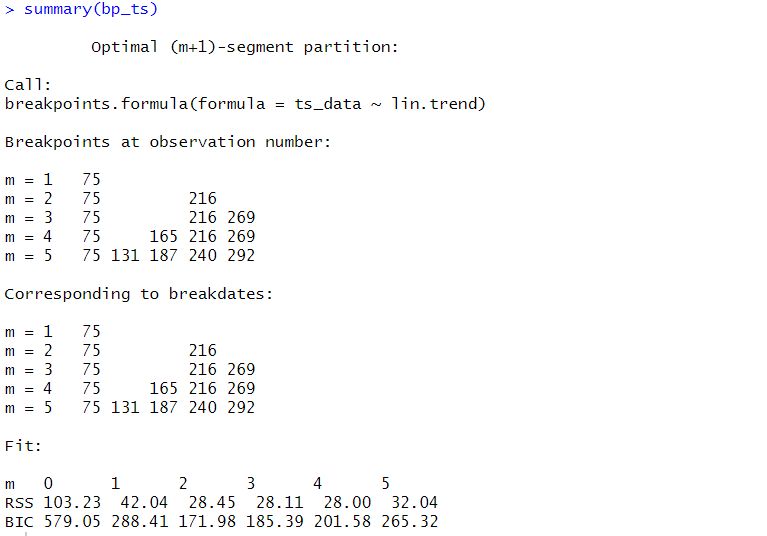
以下、実行結果です。

 

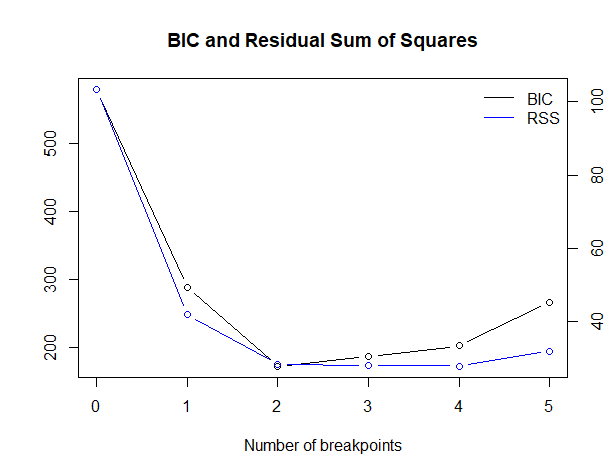
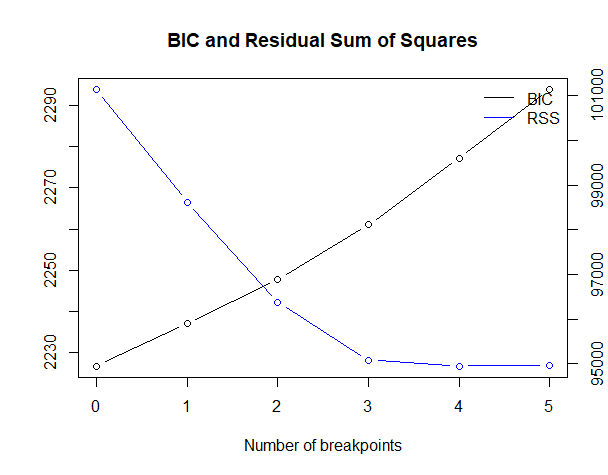
今回のケースでは、変化点が2が最適になっています。

変化点が2つの場合、以下となります。

  • 75
  • 216

グラフで視覚的に確認したいと思います。

2つの変化点で分割すると、データは3区分になります。区分ごとの回帰線を推定します。

以下、コードです。

# 回帰線の推定
coefficients(bp_ts)                                  #切片と係数
fm <- lm(ts_data ~ breakfactor(bp_ts)/(lin.trend)-1) #推定値

 

以下、実行結果です。

 

グラフで視覚的に確認したいと思います。

以下、コードです。

# プロット
ci_ts <- confint(bp_ts)        #変化点の信頼区間 
plot(ts_data)                  #対象データの描写（折れ線）
lines(bp_ts)                   #変化点の描写（縦線）
lines(ci_ts)                   #信頼区間の描写（赤）
lines(ts(fitted(fm)), col = 4) #回帰線の描写（青）

 

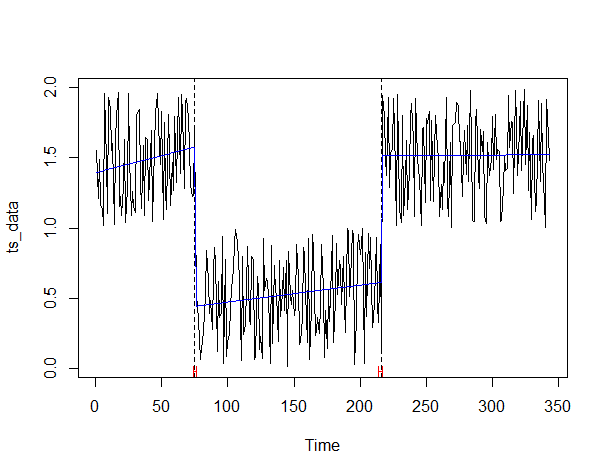
以下、実行結果です。

 

水準変化を捉え、何となく感覚的に合致するかと思います。

最後に、オブジェクトを削除します。

# オブジェクトの削除
rm(bp_ts)
rm(ci_ts)

 

データセット④「生産センサーデータ２」の変化点検知

対象データを、ts_dataに代入し変化点検知を実施していきます。

以下、コードです。

# 対象データの代入
ts_data <- Sensor2

 

変化点検知をします。

以下、コードです。

# 実行
lin.trend <- 1:length(ts_data)            #トレンド変数
bp_ts <- breakpoints(ts_data ~ lin.trend) #変化点推定

 

実行結果を確認します。

以下、コードです。

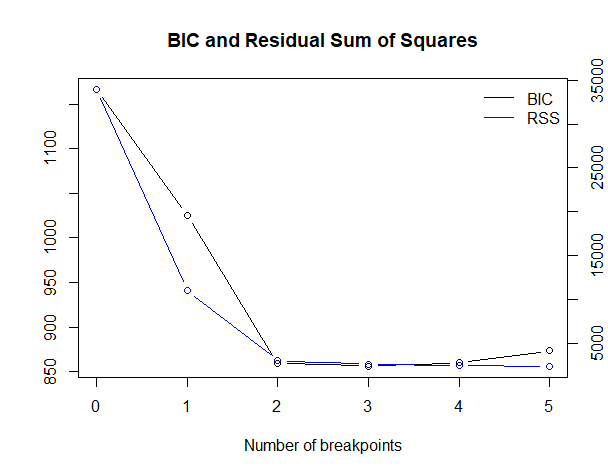
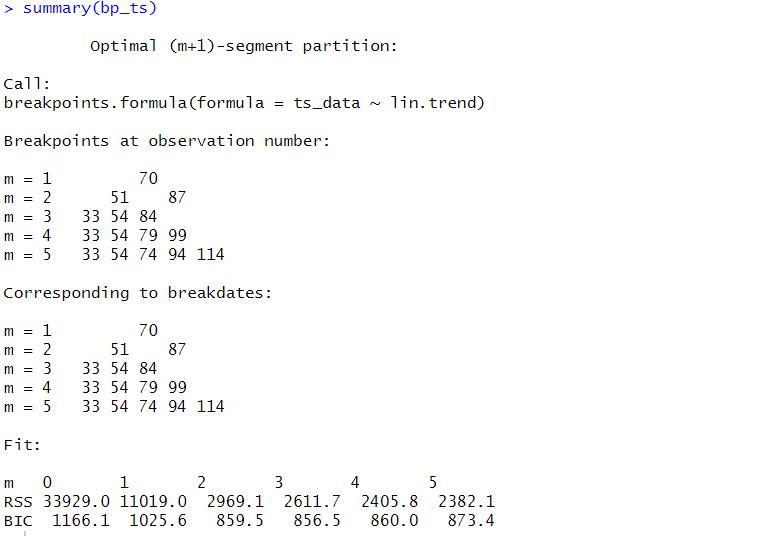
# 結果の確認
plot(bp_ts)
summary(bp_ts)

 

以下、実行結果です。

 

今回のケースでは、変化点が0が最適になっています。

変化点がないので、データは分割されず、全体で回帰線を推定します。

以下、コードです。

# 回帰線の推定
fm <- lm(ts_data ~ lin.trend) #推定値
coefficients(fm)              #切片と係数

以下、結果です。

 

グラフで視覚的に確認したいと思います。

以下、コードです。

# プロット
plot(ts_data)                  #対象データの描写（折れ線）
lines(ts(fitted(fm)), col = 4) #回帰線の描写（青）

 

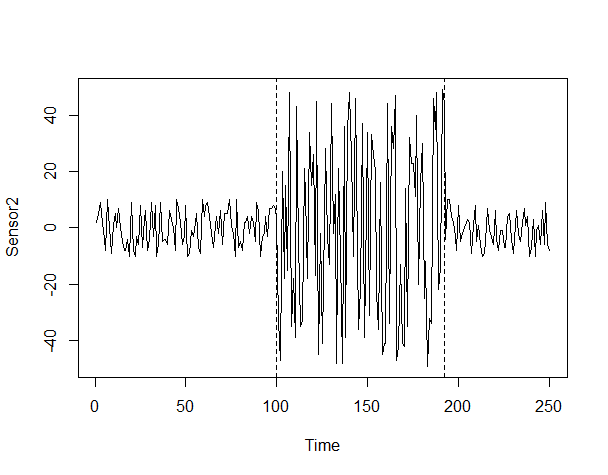
以下、実行結果です。

 

グラフを見た感じでは分散変化が起こっています。

しかし、変化点が0だったことからも、分散の検知が出来ていないことが分かります。

分散検知をするやり方は色々ありますが、ここで最も簡単な方法を説明します。先ほど推定した回帰線の残差で中心化したデータを2乗することで新たな時系列データを作ると、分散変化を検知できます。

どのようなデータになるのか、簡単にグラフ化し確認してみます。

以下、コードです。

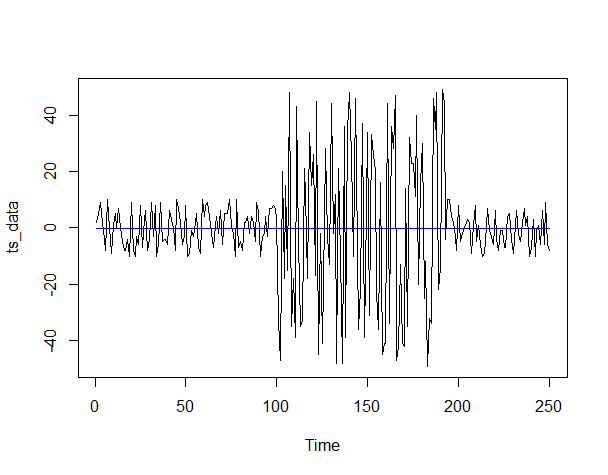
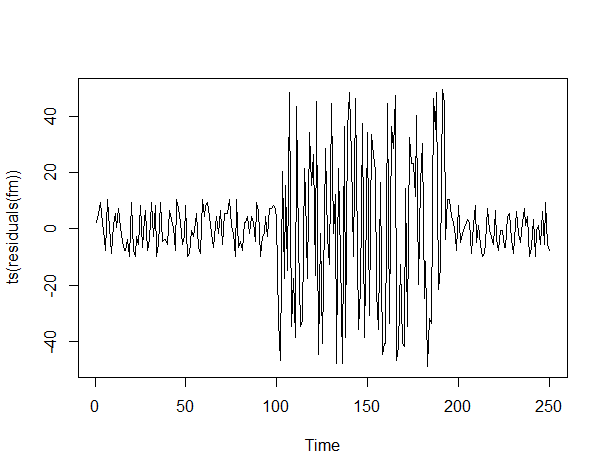
# 残差のプロット
plot(ts(residuals(fm)))

 

以下、実行結果です。

 

この残差を中心化し2乗したデータを、対象データとします。

以下、コードです。

# 対象データの代入
ts_data <- (ts_data-mean(ts_data))^2

 

変化点検知をします。

以下、コードです。

# 実行
bp_ts <- breakpoints(ts_data ~ 1) #変化点推定

 

実行結果を確認します。

以下、コードです。

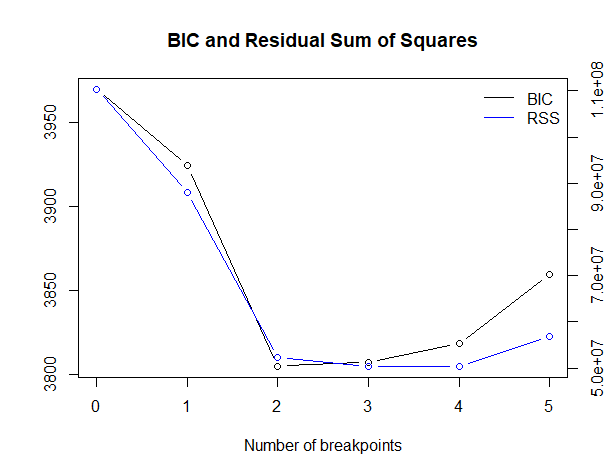
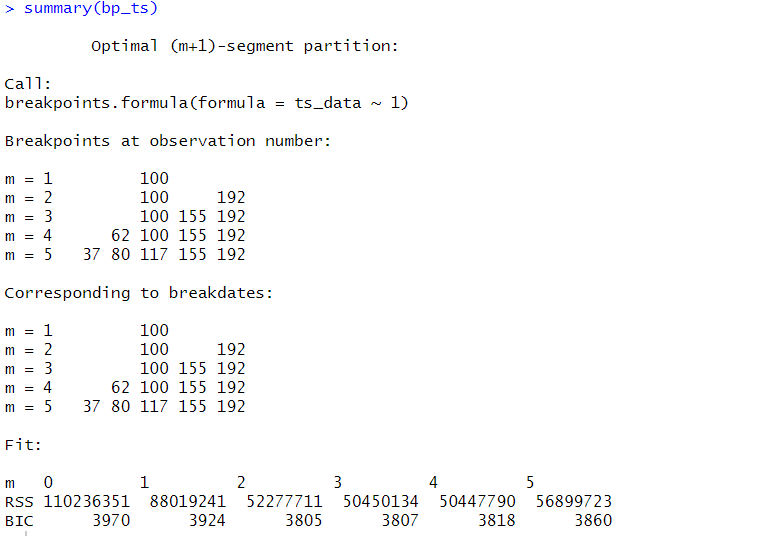
# 結果の確認
plot(bp_ts)
summary(bp_ts)

 

以下、実行結果です。

 

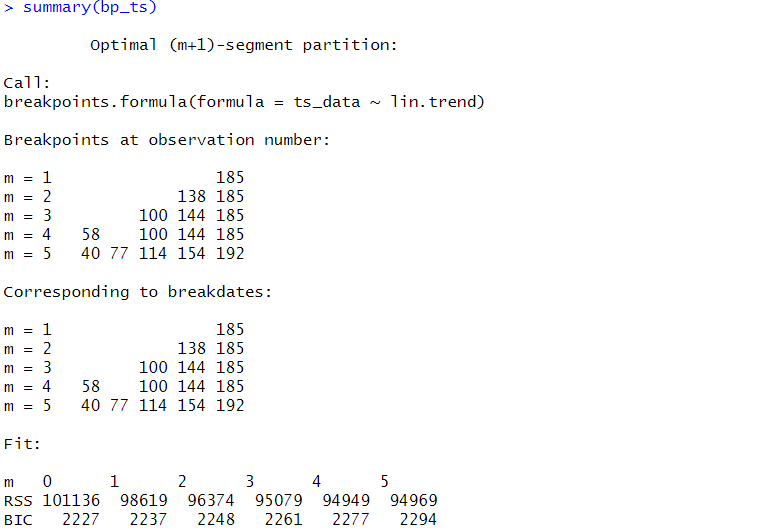
今回のケースでは、変化点が2が最適になっています。

変化点が2つの場合、以下となります。

  • 100
  • 192

2つの変化点で分割すると、データは3区分になります。区分ごとの回帰線を推定します。

以下、コードです。

# 回帰線の推定
fm <- lm(ts_data ~ breakfactor(bp_ts)-1) #推定値
coefficients(fm)                         #水準（切片）

 

以下、実行結果です。

 

グラフで視覚的に確認したいと思います。

以下、コードです。

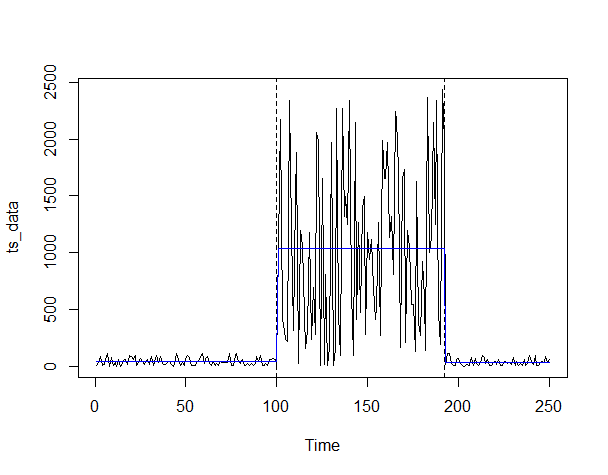
# プロット
ci_ts <- confint(bp_ts)        #変化点の信頼区間 
plot(ts_data)                  #対象データの描写（折れ線）
lines(bp_ts)                   #変化点の描写（縦線）
lines(ci_ts)                   #信頼区間の描写（赤）
lines(ts(fitted(fm)), col = 4) #回帰線の描写（青）

 

以下、実行結果です。

 

信頼区間の計算が上手くいかなかったので、表示されていません。

分かり難いので、元の時系列データ（Sensor2）上に変化点の縦線を描写します。

以下、コードです。

# プロット
plot(Sensor2)　　　          　#対象データの描写（折れ線）
lines(bp_ts)                  #変化点の描写（縦線）

 

以下、実行結果です。

 

分散変化を捉え、何となく感覚的に合致するかと思います。

最後に、オブジェクトを削除します。

# オブジェクトの削除
rm(bp_ts)
rm(ci_ts)

 

まとめ

今回は、「Rでサクッと時系列データの変化点を見つける方法」というお話しをしました。

ビジネスの世界のデータの多くは、時間軸のあるデータである時系列データです。

時系列データを手に入れたら、どのようなデータかなんとなく知りたくなります。その1つが構造が変化する時期（変化点）です。

Rのライブラリーには、時系列データの変化点を検知することのできるものが色々あります。例えば、strucchangeです。興味のある方は、試して頂ければと思います。