Rで推定するパレート分布

「第222話｜パレート指数による売上分析」でパレート分布についてお話ししました。

ビジネスはパレートな世界の住人でしょう。

例えば……

チェーン店であれば、極端に売上の大きい店舗はあります
営業パーソンであれば、極端に受注額の大きい人はいます
顧客であれば、極端に取引額の大きい得意先はあります
商品であれば、極端に利益額の大きい商品はあります
日販であれば、極端に売上高の高い日はあります

……などなど。

どのようにして、得られたデータからパレート分布を推定するのかを説明します。

Contents

3つのパッケージ
パッケージのインストール
Newdistnsパッケージ
ライブラリーの読み込み（ロード）
指数化パレート分布
指数化パレート分布の形状の確認
指数化パレート分布の推定
ベータパレート分布
ベータパレート分布の形状の確認
ベータパレート分布の推定
一般化ベータパレート分布
一般化ベータパレート分布の形状の確認
一般化ベータパレート分布の推定
まとめ

3つのパッケージ

パレート分布に関するパッケージは、Rには色々あります。

今回は、パッケージ「Newdistns」を利用します。

パレート分布といっても色々と進化し、他の確率分布と一緒くた（同じ枠組みでくくられ）になっています。

パッケージ「Newdistns」では、色々なパレート分布（一般化パレート分布や指数化パレート分布などを含む）を表現できます。

パッケージのインストール

今回は、次の2つのパッケージを使います。

Newdistns
ggplot2

まだ、インストールされていない方は、インストールして頂ければと思います。

install.packages("Newdistns", dependencies = TRUE)
install.packages("ggplot2", dependencies = TRUE)

Newdistnsパッケージ

パッケージ「Newdistns」には、色々な分布族の確率密度関数（pdf）や累積分布関数（cdf）、乱数の発生、分布の推定ができます。

例えば、以下の分布族です。

Marshall Olkin G分布
指数G分布
ベータG分布
ガンマG分布
Kumaraswamy G分布
一般化ベータG分布
ベータ拡張G分布
ガンマG分布
ガンマ一様G分布
ベータ指数G分布
ワイブルG分布
対数ガンマG I分布
対数ガンマG II分布
指数化一般化G分布
指数化G分布
指数化 Kumaraswamy G分布
幾何学的指数ポアソンG分布
切り捨て指数 skew-symmetric G分布
修正ベータG分布
指数化指数ポアソンG分布

要するに、色々あるということです。

例えば……

指数化パレート分布は「指数化G分布」
ベータ系のパレート分布であれば「ベータG分布」や「一般化ベータG分布」
Kumaraswamy系のパレート分布であれば「Kumaraswamy G分布」や「指数化 Kumaraswamy G分布」
ワイブルパレート分布であれば「ワイブルG分布」

ライブラリーの読み込み（ロード）

先ず、ライブラリーの読み込み（ロード）ます。

以下、コードです。

library(Newdistns)
library(ggplot2)

次の3つのパレート分布を対象にします。

指数化パレート分布：「指数化G分布」（expg）、パラメータが1つ
ベータパレート分布：「ベータG分布」（betag）、パラメータが2つ
一般化ベータパレート分布：「一般化ベータG分布」（gbg）、パラメータが3つ

指数化パレート分布

以下、関数です。

dexpg：確率密度関数
pexpg：累積分布関数
qexpg：累積分布関数の逆関数
rexpg：乱数発生
mexpg：分布推定

指数化パレート分布の形状の確認

どのような分布なのか、確認してみます。

以下、コードです。

p <- ggplot(data=data.frame(X=c(0,10)), 
            aes(x=X))
p <- p + stat_function(fun=dexpg, 
                       args=list("exp",a=2),
                       size=1)
p

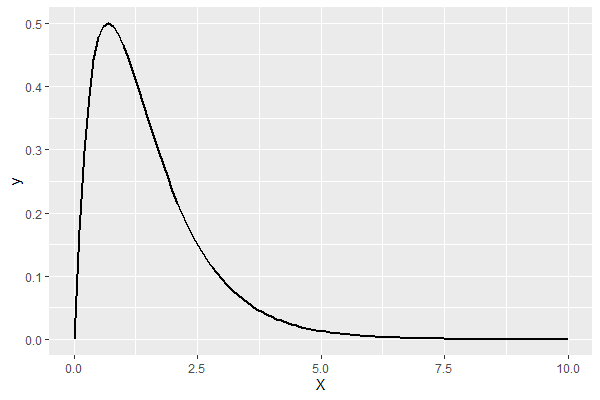
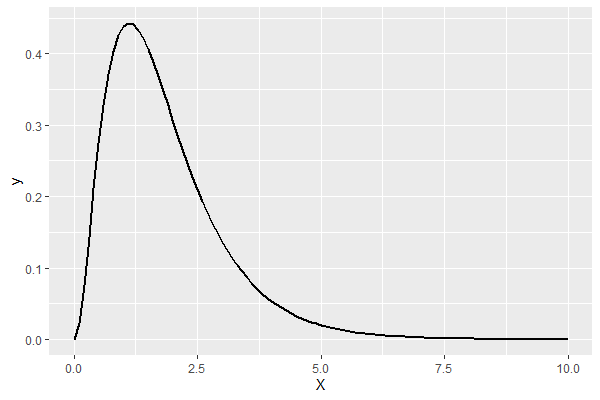
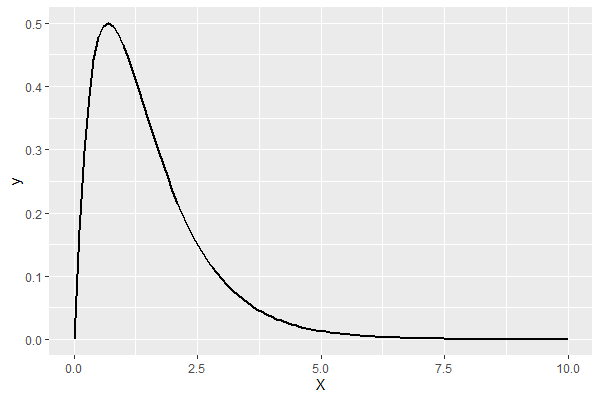
以下、実行結果です。

パラメータa（パレート指数）を変化させてみます。

以下、コードです。

p <- ggplot(data=data.frame(X=c(0,10)), 
            aes(x=X))
p <- p + stat_function(fun=dexpg, 
                       args=list("exp",a=1),
                       size=1,
                       col=1)
p <- p + stat_function(fun=dexpg, 
                       args=list("exp",a=2),
                       size=1,
                       col=2)
p

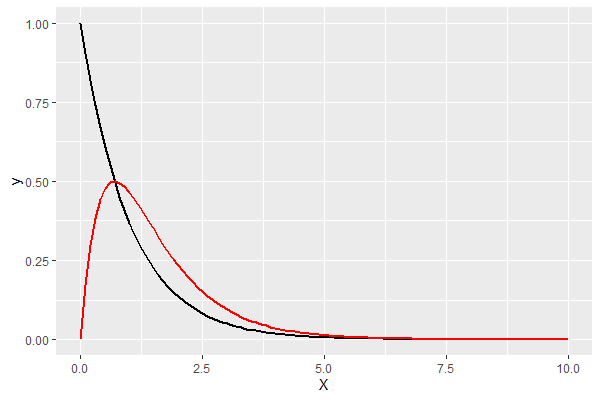
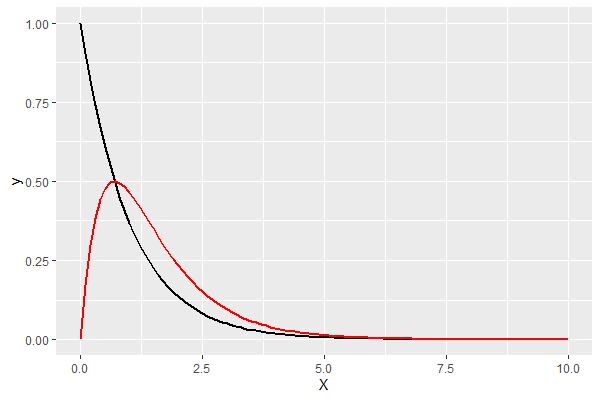
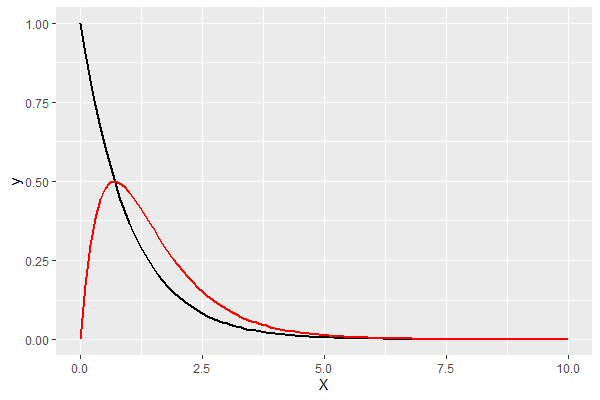
以下、実行結果です。

a=1：黒
a=2：赤

所得などの分布を表現できそうなことが分かります。

指数化パレート分布の推定

先ず、乱数を発生させサンプルデータを作ります。

以下、コードです。

dat1 <- rexpg(1000,"exp",a=3)

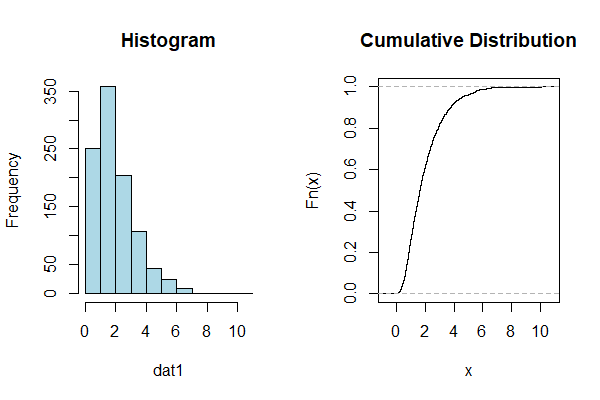
次に、サンプルデータ「dat1」の分布を可視化してみます。ヒストグラムと累積分布です。

以下、コードです。

par(mfrow=c(1,2))
hist(dat1,col="lightblue",main="Histogram")
plot(ecdf(dat1),main="Cumulative Distribution")

以下、実行結果です。

このサンプルデータに対しパレート分布を推定したいと思います。

以下、コードです。

fit1 <- mexpg("exp",dat1,starts=c(1,1),method="BFGS")

推定結果を見てみます。

以下、コードです。

fit1

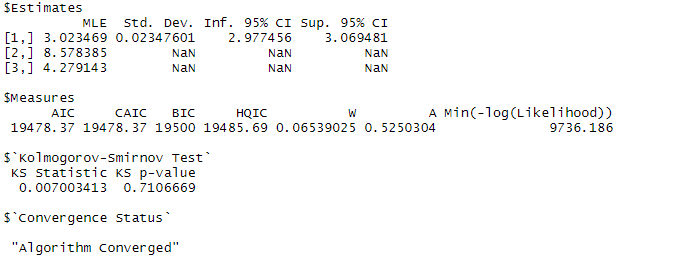
以下、実行結果です。

「$Estimates」の「MLE」が推定結果（点推定）です。

この推定結果を使い、パレート分布を描いてみます。

以下、コードです。

a <- fit1$Estimates[1,1]

p <- ggplot(data=data.frame(X=c(0,10)), 
            aes(x=X))
p <- p + stat_function(fun=dexpg, 
                       args=list("exp",a=a),
                       size=1)
p

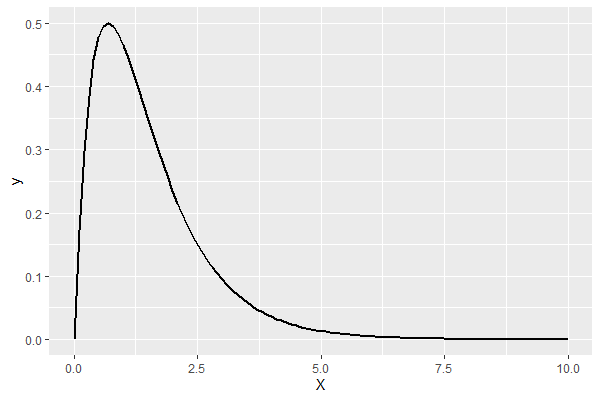
以下、実行結果です。

ベータパレート分布

以下、関数です。

dbetag：確率密度関数
pbetag：累積分布関数
qbetag：累積分布関数の逆関数
rbetag：乱数発生
mbetag：分布推定

ベータパレート分布の形状の確認

どのような分布なのか、確認してみます。

以下、コードです。

p <- ggplot(data=data.frame(X=c(0,10)), 
            aes(x=X))
p <- p + stat_function(fun=dbetag, 
                       args=list("exp",a=2,b=1),
                       size=1)
p

以下、実行結果です。

パラメータaを変化させてみます。

以下、コードです。

p <- ggplot(data=data.frame(X=c(0,10)), 
            aes(x=X))
p <- p + stat_function(fun=dbetag, 
                       args=list("exp",a=1,b=1),
                       size=1,
                       col=1)
p <- p + stat_function(fun=dbetag, 
                       args=list("exp",a=2,b=1),
                       size=1,
                       col=2)
p

以下、実行結果です。

a=1：黒
a=2：赤

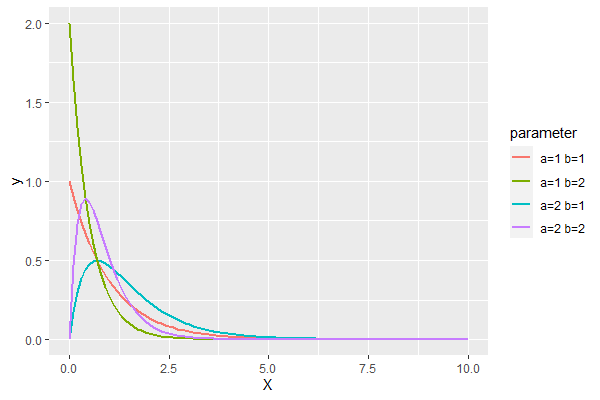
パラメータaとbを変化させてみます。

以下、コードです。

ab <- expand.grid(a=c(1, 2), 
                  b=c(1, 2))

p <- ggplot(data.frame(X=c(0, 10)), aes(x=X)) +
  mapply(
    function(a, b, co) 
      stat_function(fun=dbetag, 
                    args=list("exp",a=a,b=b), 
                    aes_q(color=co), 
                    size=1),
    ab$a, 
    ab$b, 
    sprintf("a=%.0f b=%.0f", ab$a, ab$b)
  )
p <- p + labs(color="parameter")
p

以下、実行結果です。

ベータパレート分布の推定

先ず、乱数を発生させサンプルデータを作ります。

以下、コードです。

dat2 <- rbetag(1000,"exp",a=3,b=1)

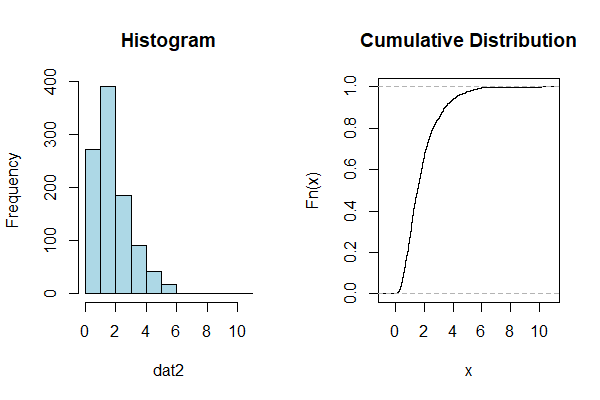
次に、サンプルデータ「dat2」の分布を可視化してみます。ヒストグラムと累積分布です。

以下、コードです。

par(mfrow=c(1,2))
hist(dat2,col="lightblue",main="Histogram")
plot(ecdf(dat2),main="Cumulative Distribution")

以下、実行結果です。

このサンプルデータに対しパレート分布を推定したいと思います。

以下、コードです。

fit2 <- mbetag("exp",dat2,starts=c(1,1,1),method="BFGS")

推定結果を見てみます。

以下、コードです。

fit2

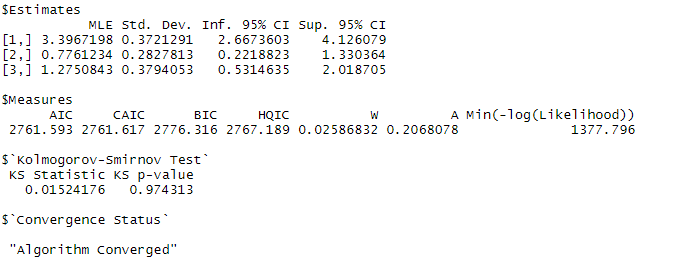
以下、実行結果です。

「$Estimates」の「MLE」が推定結果（点推定）です。

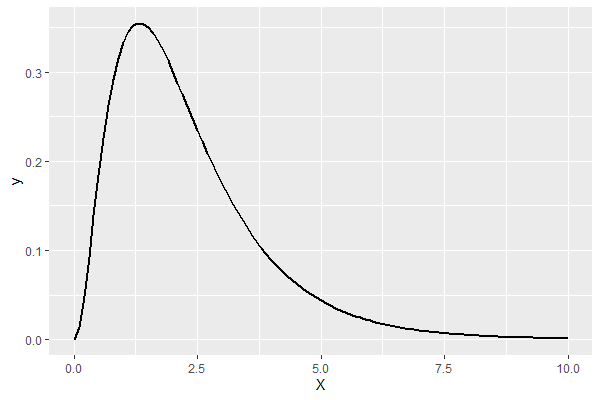
この推定結果を使い、パレート分布を描いてみます。

以下、コードです。

a = fit2$Estimates[1,1]
b = fit2$Estimates[2,1]

p <- ggplot(data=data.frame(X=c(0,10)), 
            aes(x=X))
p <- p + stat_function(fun=dbetag, 
                       args=list("exp",a=a,b=b),
                       size=1)
p

以下、実行結果です。

一般化ベータパレート分布

以下、関数です。

dgbg：確率密度関数
pgbg：累積分布関数
qgbg：累積分布関数の逆関数
rgbg：乱数発生
mgbg：分布推定

一般化ベータパレート分布の形状の確認

どのような分布なのか、確認してみます。

以下、コードです。

p <- ggplot(data=data.frame(X=c(0,10)), 
            aes(x=X))
p <- p + stat_function(fun=dgbg, 
                       args=list("exp",a=2,b=1,c=1),
                       size=1)
p

以下、実行結果です。

パラメータaを変化させてみます。

以下、コードです。

p <- ggplot(data=data.frame(X=c(0,10)), 
            aes(x=X))
p <- p + stat_function(fun=dgbg, 
                       args=list("exp",a=1,b=1,c=1),
                       size=1,
                       col=1)
p <- p + stat_function(fun=dgbg, 
                       args=list("exp",a=2,b=1,c=1),
                       size=1,
                       col=2)
p

以下、実行結果です。

a=1：黒
a=2：赤

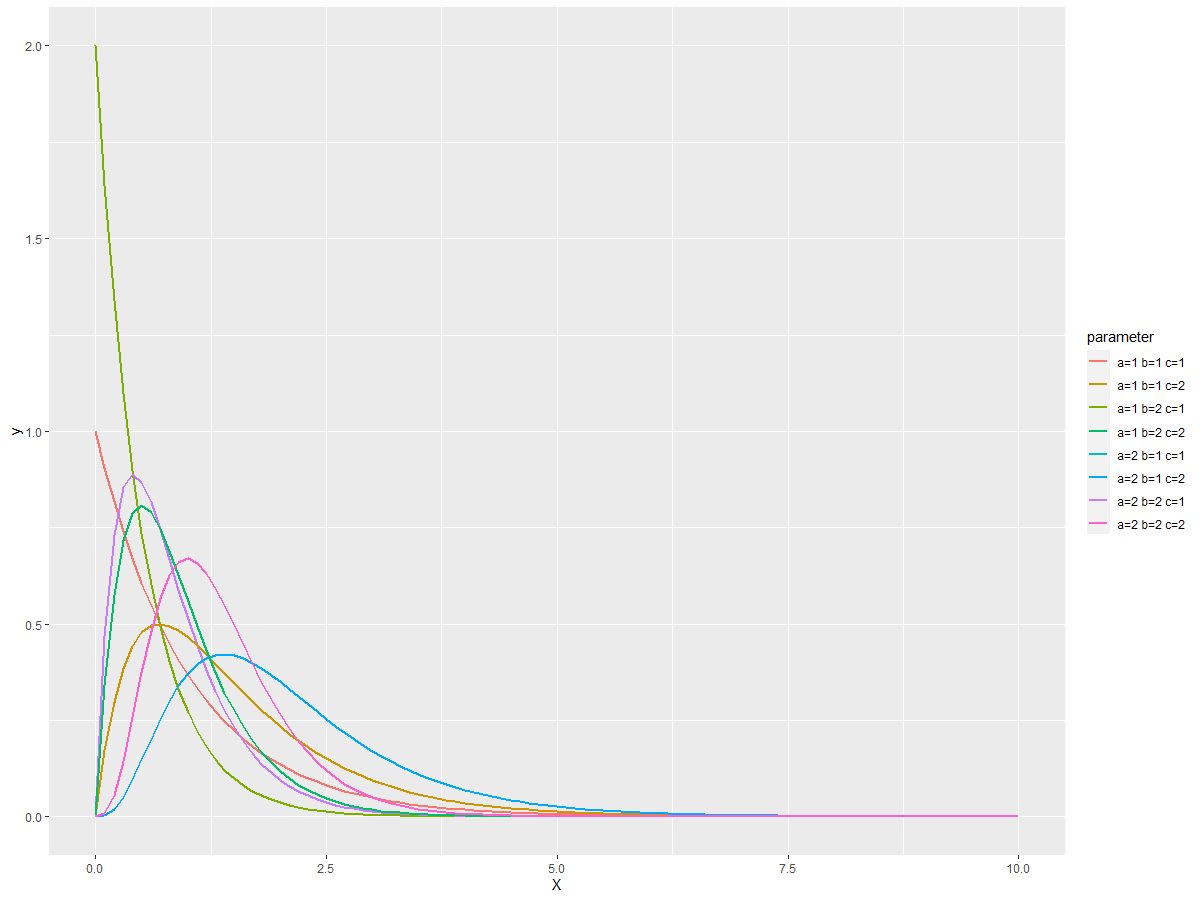
パラメータaとbとcを変化させてみます。

以下、コードです。

abc <- expand.grid(a=c(1, 2), 
                   b=c(1, 2), 
                   c=c(1, 2))

p <- ggplot(data.frame(X=c(0, 10)), aes(x=X)) +
  mapply(
    function(a, b, c, co) 
      stat_function(fun=dgbg, 
                    args=list("exp",a=a,b=b,c=c), 
                    aes_q(color=co), 
                    size=1),
    abc$a, 
    abc$b, 
    abc$c, 
    sprintf("a=%.0f b=%.0f c=%.0f", abc$a, abc$b, abc$c)
  )
p <- p + labs(color="parameter")
p

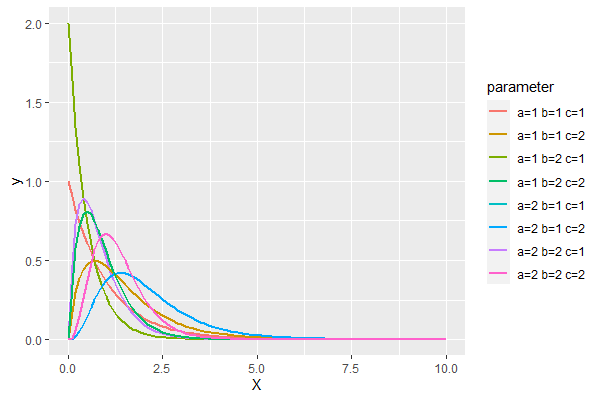
以下、実行結果です。

一般化ベータパレート分布の推定

先ず、乱数を発生させサンプルデータを作ります。

以下、コードです。

dat3 <- rgbg(1000,"exp",a=2,b=2,c=2)

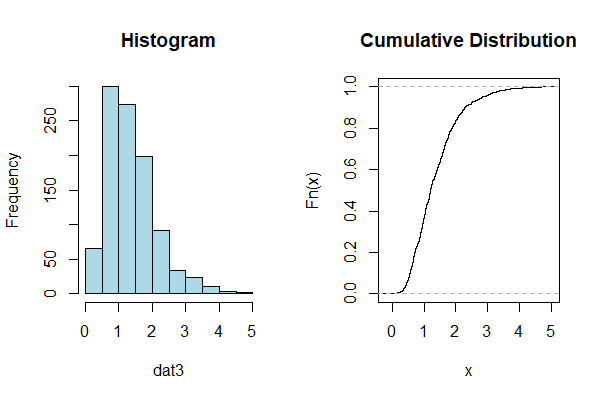
次に、サンプルデータ「dat3」の分布を可視化してみます。ヒストグラムと累積分布です。

以下、コードです。

par(mfrow=c(1,2))
hist(dat3,col="lightblue",main="Histogram")
plot(ecdf(dat3),main="Cumulative Distribution")

以下、実行結果です。

このサンプルデータに対しパレート分布を推定したいと思います。

以下、コードです。

fit3 <- mexpkumg("exp",dat3,starts=c(1,1,1,1),method="BFGS")

推定結果を見てみます。

以下、コードです。

fit3

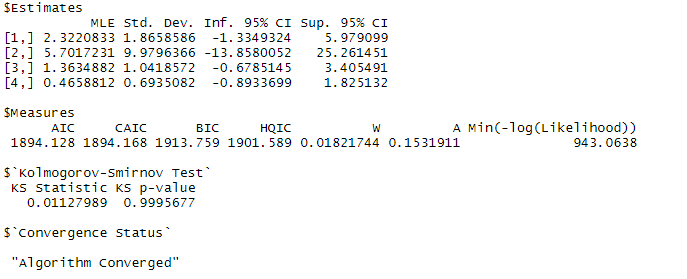
以下、実行結果です。

「$Estimates」の「MLE」が推定結果（点推定）です。

この推定結果を使い、パレート分布を描いてみます。

以下、コードです。

a = fit3$Estimates[1,1]
b = fit3$Estimates[2,1]
c = fit3$Estimates[3,1]

p <- ggplot(data=data.frame(X=c(0,10)), 
            aes(x=X))
p <- p + stat_function(fun=dgbg, 
                       args=list("exp",a=a,b=b,c=c),
                       size=1)
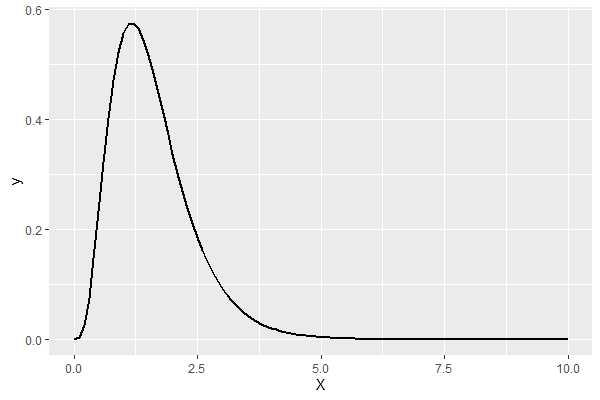
p

以下、実行結果です。