RStudio(R)×Keras(TensorFlow)によるお手軽ディープラーニングその1（分類問題）

8296
RStudio(R)×Keras(TensorFlow)によるお手軽ディープラーニングその1（分類問題）

Rにはディープラーニング関連のパッケージが色々あります。

例えば……

  • neuralnet
  • nnet
  • RSNNS
  • deepnet
  • darch
  • rnn
  • FCNN4R
  • rcppDL
  • deepr
  • MXNetR
  • h2o
  • tensorflow
  • keras

……などなど。

R独自のものから、そうでないものもあります。

今回はKeras(TensorFlow)をRStudio(R)上で使い、分類問題に対しニューラルネットワーク型のディープラーニングを構築していたいと思います。

Kerasというライブラリでニューラルネットワークを設計し、バックエンドでTensorFlowというディープラーニングライブラリが動き計算します。

回帰問題に関しては、次回お話しします。

RStudio(R)×Keras(TensorFlow)によるお手軽ディープラーニングその2（回帰問題）

KerasとTensorFlowのインストール

以下、Kerasをインストールするときのコードです。

# Kerasのインストール
install.packages("keras", dependencies = TRUE)

 

以下、TensorFlowをインストールするときのコードです。

# TensorFlowのインストール
library(keras)
install_keras()

 

もしくは、以下でもインストールできます。

library(tensorflow)
install_tensorflow()

 

TensorFlowのバージョン指定や、GPU指定もできます。特に指定しないと、CPU版になります。

ちなみに、今回はTensorFlow関連のお話しや、数理的なお話しは一切しません。興味のある方は、以下を参考にしてください。

R Interface to Tensorflow: Guide
https://tensorflow.rstudio.com/guide/

Tensorflow
https://www.tensorflow.org/

 

データセット

今回利用するデータセットは、分類問題でよく登場するみんな大好き「アヤメ（iris）」データセットです。

Rに最初から搭載されているサンプルデータです。何もしなくても使えます。

以下、データ項目です。

  • sepal.length：ガクの長さ
  • sepal.width：ガクの幅
  • petal.length：花弁の長さ
  • petal.width：花弁の幅
  • species：花の種類

項目数は5。

  • 目的変数Y：一番下の「species」（花の種類）
  • 説明変数X（特徴量）：残り4つのデータすべて

要するに、「species」（花の種類）を他の変数で当てる問題です。

 

ライブラリーのロード

先ず最初に、必要なライブラリーを読み込みます。

以下、コードです。

# 必要パッケージのロード
library(keras)     #keras
library(neuralnet) #NN図示化するときに利用
library(tidyverse) #基本ライブラリー
library(magrittr)  #基本ライブラリー

 

準備

前処理①：型変換

データセットを整えます。

以下、コードです。

# データセットの読み込み
dataset <- iris
str(dataset) #確認用

 

以下、実行結果です。

 

データの中に、因子型（factor）が混じっています。数値型へ変換しておく必要があるため、変換します。

以下、コードです。

# 型変換
## 因子型を数値型に変換
dataset %<>% mutate_if(is.factor, as.numeric)
str(dataset) #確認用

 

以下、実行結果です。

 

今回は、型変換を特殊なやり方で実施しています。因子型が複数あったときに、一度に数値型へ変換するやり型です。データ項目数が多いときに便利です。

 

さらに、データセットをデータフレームからマトリックに変換します。

以下、コードです。

## Matrix型へ変換
dataset <- as.matrix(dataset)
dimnames(dataset) <- NULL

 

データセットの分割（学習データとテストデータ）

次に、学習データとテストデータに分割します。

モデルは学習データで構築し、その構築したモデルの精度をテストデータで検証します。

以下、コードです。

# 学習データとテストデータに分割
set.seed(123)
ind <- sample(2, nrow(dataset), replace = T, prob = c(0.75, 0.25))
## 学習データ
X_train <- dataset[ind==1, 1:4]
y_train <- dataset[ind==1, 5] - 1
## テストデータ
X_test <- dataset[ind==2, 1:4]
y_test <- dataset[ind==2, 5] - 1
  • X_train：学習データの説明変数X（特徴量）
  • y_train：学習データの目的変数y
  • X_test：テストデータの説明変数X（特徴量）
  • y_test：テストデータの目的変数y

目的変数yから1引いているのは、目的変数の値が「1, 2, 3」と1から始まる状態を避け、0から始める状態「0, 1, 2」にするためです。

 

前処理②：目的変数yのダミー変数化

目的変数yは、カテゴリカルであるためダミー変数にします。

# 目的変数yのダミー化
y_train_d <- to_categorical(y_train)
y_test_d <- to_categorical(y_test)
head(y_train_d) #確認用

 

以下、実行結果です。

 

実は、目的変数の値が「1, 2, 3」のままだとこのダミー化が上手くいかず、4変量になります。そのため先ほど「0, 1, 2」のようにしました。

 

前処理③：説明変数X（特徴量）の標準化

次に、説明変数X（特徴量）も加工します。標準化です。

以下、コードです。

# 説明変数Xの標準化
m <- apply(X_train, 2, mean)
s <- apply(X_train, 2, sd)
X_train <- scale(X_train, center = m, scale = s)
X_test <- scale(X_test, center = m, scale = s)

 

これで準備は終了です。

コード全体（ライブラリーの読み込みから前処理まで）

# データセットの読み込み
dataset <- iris
str(dataset) #確認用

# 型変換
## 因子型を数値型に変換
dataset %<>% mutate_if(is.factor, as.numeric)
str(dataset) #確認用
## Matrix型へ変換
dataset <- as.matrix(dataset)
dimnames(dataset) <- NULL

# 学習データとテストデータに分割
set.seed(123)
ind <- sample(2, nrow(dataset), replace = T, prob = c(0.75, 0.25))
## 学習データ
X_train <- dataset[ind==1, 1:4]
y_train <- dataset[ind==1, 5] - 1
## テストデータ
X_test <- dataset[ind==2, 1:4]
y_test <- dataset[ind==2, 5] - 1

# 目的変数yのダミー化
y_train_d <- to_categorical(y_train)
y_test_d <- to_categorical(y_test)
head(y_train_d)

# 説明変数Xの標準化
m <- apply(X_train, 2, mean)
s <- apply(X_train, 2, sd)
X_train <- scale(X_train, center = m, scale = s)
X_test <- scale(X_test, center = m, scale = s)

 

3つの予測モデル

今回は、3つのニューラルネットワーク型のモデルを構築します。

  • モデル①：3層型　入力層→隠れ層→出力層
  • モデル②：4層型　入力層→隠れ層1→隠れ層2→出力層
  • モデル③：Dropout層付き4層型　入力層→隠れ層1→(Dropout層)→隠れ層2→(Dropout層)→出力層

シンプルなもの、やや複雑化したもの、過学習を緩和したものです。

Dropout層とは、過学習を緩和するための工夫で、モデルの学習時に隠れ層から出力される値を設定した割合でゼロにします。適切に設定すると、学習データに対する精度は悪化しますがテストデータに対する精度は良くなります。

 

モデル①（3層型）

モデル①：学習（学習データ利用）

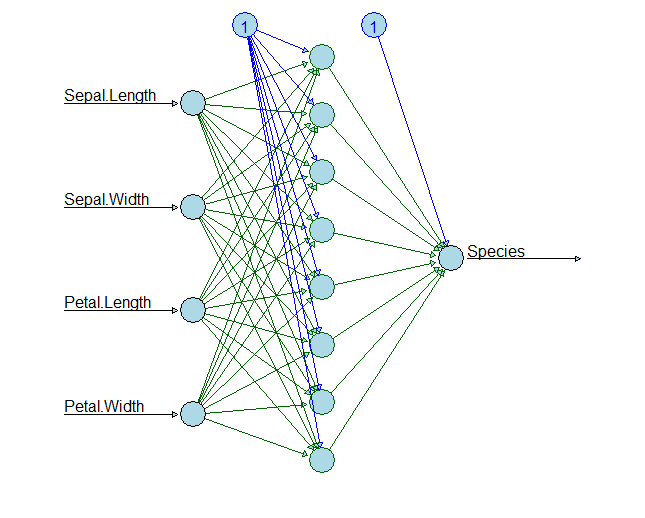
「入力層→隠れ層→出力層」のニューラルネットワーク型のディープラーニングのモデルを構築していきます。

  • 入力層のユニット数：4（説明変数Xの数）
  • 隠れ層のユニット数：8
  • 出力層のユニット数：3（目的変数yは1つだが、3カテゴリーあるため）

各層の活性化関数（activation）は……

  • 隠れ層：selu（Scaled Exponential Linear Unit）
  • 出力層：softmax

以下、コードです。

# モデル構築
## モデル定義
model <- keras_model_sequential() 
model %>% 
  #隠れ層
  layer_dense(units = 8, 
              activation = 'selu', 
              input_shape = c(4)) %>% 
  #出力層
  layer_dense(units = 3, 
              activation = 'softmax') 

summary(model) #確認用

 

以下、実行結果です。

 

定義通りになっているのか確認しておきましょう。

  • 入力層→隠れ層のパラメータ：(4+1)×8=40
  • 隠れ層→出力層のパラメータ：(8+1)×3=27

 

次に、コンパイルし学習します。

以下、コードです。

## コンパイル
model %>% compile(loss = 'categorical_crossentropy',
                  optimizer = 'adam',
                  metrics = 'accuracy')

## 学習
history <- 
  model %>% fit(X_train, 
                y_train_d, 
                epochs = 100,
                batch_size = 10, 
                validation_split = 0.25)

history #確認用

 

以下、実行中の画像です。

 

以下、実行結果です。

 

Kerasはモデル学習時に、学習データをさらに2つに分割します。

  • train data：ニューラルネットワークのパラメータを学習するときに用いるデータ
  • validation data：学習したパラメータの良し悪しを確かめるためのデータ

学習データもtrain dataと訳されるので紛らわしいですが……

分割の割合は「validation_split 」で指定します。今回は「validation_split = 0.25」となっているので、train dataが75%で、validation dataが25%です。

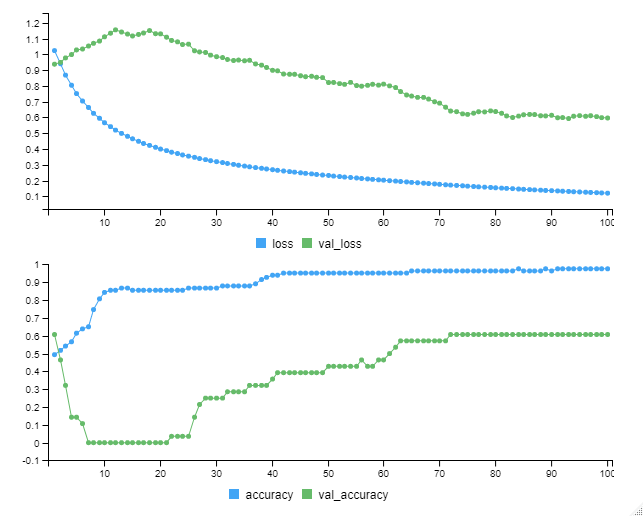
今回学習したモデルの学習データセットの正答率は……

  • train dataの正答率（accuracy）：97.59%
  • validation dataの正答率（val_accuracy）：60.71%

 

補足です。

エポック（epoch）とバッチ（batch）のお話しです。

Kerasはモデル学習時にtrain dataをすべて使うわけではなく、train dataをいくつかのバッチ（データの塊）に分割し、そのバッチ（データの塊）ごとに学習を実施していきます。

バッチのサイズは、「batch_size」で指定します。今回は「batch_size=10」としています。

例えば、train dataが1,000あったとき、サイズが10の100（=1,000÷10）個のバッチ（データの塊）に分割されます。100（=1,000÷10）個のバッチ（データの塊）による学習すべてを終えると、1エポック（epoch）です。

このエポックを何回繰り返すのかは、「epochs」で指定します。今回は「epochs = 100」としています。

 

モデル①：検証（テストデータ利用）

モデルが構築できたので、テストデータを使い予測し検証していきたいと思います。

先ず、テストデータの説明変数X（特徴量）を使い、目的変数yを予測します。

以下、コードです。

# 予測（検証）
## テストデータの予測
pred_y_test <- 
  model %>% 
  predict_classes(X_test)

 

どのくらいの精度で当てられたのか、混同行列（実測値と予測値の集計表）を使い見ていきます。

以下、コードです。

## 混同行列
table(y_test, pred_y_test)

 

以下、実行結果です。

 

いい感じで予測できていることが分かります。

では、どのくらい正解したのか、正答率を計算してみます。

以下、コードです。

## 正答率
model %>% 
  evaluate(X_test, y_test_d)

 

以下、実行結果です。

 

正答率は87.18%でした。

 

モデル①：コード全体（モデル構築から検証まで）

#
# モデル1
#

# モデル構築
## モデル定義
model <- keras_model_sequential() 
model %>% 
  #隠れ層
  layer_dense(units = 8, 
              activation = 'selu', 
              input_shape = c(4)) %>% 
  #出力層
  layer_dense(units = 3, 
              activation = 'softmax') 

summary(model) #確認用

## コンパイル
model %>% compile(loss = 'categorical_crossentropy',
                  optimizer = 'adam',
                  metrics = 'accuracy')

## 学習
history <- 
  model %>% fit(X_train, 
                y_train_d, 
                epochs = 100,
                batch_size = 10, 
                validation_split = 0.25)

history #確認用

# 予測（検証）
## テストデータの予測
pred_y_test <- 
  model %>% 
  predict_classes(X_test)
## 混同行列
table(y_test, pred_y_test)
## 正答率
model %>% 
  evaluate(X_test, y_test_d)

 

モデル②（4層型）

モデル②：学習（学習データ利用）

「入力層→隠れ層1→隠れ層2→出力層」のニューラルネットワーク型のディープラーニングのモデルを構築していきます。

  • 入力層のユニット数：4（説明変数Xの数）
  • 隠れ層1のユニット数：12
  • 隠れ層2のユニット数：7
  • 出力層のユニット数：3（目的変数yは1つだが、3カテゴリーあるため）

各層の活性化関数（activation）は……

  • 隠れ層1：selu（Scaled Exponential Linear Unit）
  • 隠れ層2：relu（REctified Linear Unit）
  • 出力層：softmax

以下、コードです。

# モデル構築
## モデル定義
model <- keras_model_sequential() 
model %>%
  #隠れ層1
  layer_dense(units = 12, 
              activation = 'selu', 
              input_shape = c(4)) %>%
  #隠れ層2
  layer_dense(units = 7, 
              activation = 'relu')  %>%
  #出力層
  layer_dense(units = 3, 
              activation = 'softmax')

summary(model)  #確認用

 

以下、実行結果です。

 

定義通りになっているのか確認しておきましょう。

  • 入力層→隠れ層1のパラメータ：(4+1)×12=60
  • 隠れ層1→出力層2のパラメータ：(12+1)×7=91
  • 隠れ層2→出力層のパラメータ：(7+1)×3=24

 

次に、コンパイルし学習します。

以下、コードです。

## コンパイル
model %>% compile(loss = 'categorical_crossentropy',
                  optimizer = 'adam',
                  metrics = 'accuracy')

## 学習
history <- 
  model %>% fit(X_train, 
                y_train_d, 
                epochs = 100,
                batch_size = 10, 
                validation_split = 0.25)

history #確認用

 

以下、実行中の画像です。

 

以下、実行結果です。

 

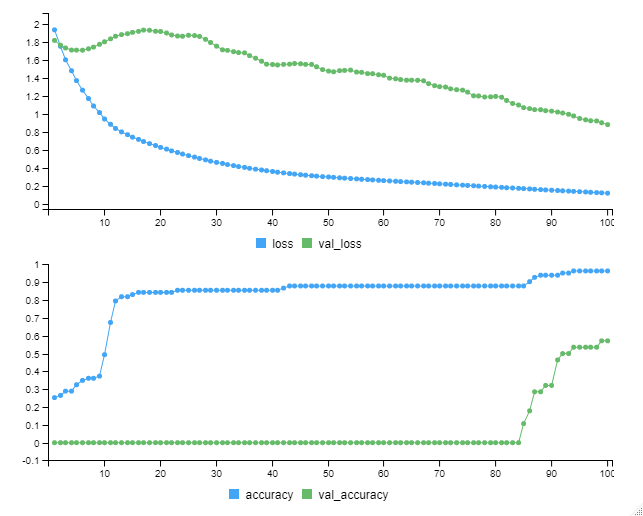
今回学習したモデルの学習データセットの正答率は……

  • train dataの正答率（accuracy）：96.39%
  • validation dataの正答率（val_accuracy）：57.14%

 

モデル②：検証（テストデータ利用）

モデルが構築できたので、テストデータを使い予測し検証していきたいと思います。

先ず、テストデータの説明変数X（特徴量）を使い、目的変数yを予測します。

以下、コードです。

# 予測（検証）
## テストデータの予測
pred_y_test <- 
  model %>% 
  predict_classes(X_test)

 

どのくらいの精度で当てられたのか、混同行列（実測値と予測値の集計表）を使い見ていきます。

以下、コードです。

## 混同行列
table(y_test, pred_y_test)

 

以下、実行結果です。

 

いい感じで予測できていることが分かります。

では、どのくらい正解したのか、正答率を計算してみます。

以下、コードです。

## 正答率
model %>% 
  evaluate(X_test, y_test_d)

 

以下、実行結果です。

 

正答率は84.61%でした。

 

モデル②：コード全体（モデル構築から検証まで）

#
# モデル2
#

# モデル構築
## モデル定義
model <- keras_model_sequential() 
model %>%
  #隠れ層1
  layer_dense(units = 12, 
              activation = 'selu', 
              input_shape = c(4)) %>%
  #隠れ層2
  layer_dense(units = 7, 
              activation = 'relu')  %>%
  #出力層
  layer_dense(units = 3, 
              activation = 'softmax')

summary(model)  #確認用

## コンパイル
model %>% compile(loss = 'categorical_crossentropy',
                  optimizer = 'adam',
                  metrics = 'accuracy')

## 学習
history <- 
  model %>% fit(X_train, 
                y_train_d, 
                epochs = 100,
                batch_size = 10, 
                validation_split = 0.25)

history #確認用

# 予測（検証）
## テストデータの予測
pred_y_test <- 
  model %>% 
  predict_classes(X_test)
## 混同行列
table(y_test, pred_y_test)
## 正答率
model %>% 
  evaluate(X_test, y_test_d)

 

モデル③（Dropout層付き4層型）

モデル③：学習（学習データ利用）

「入力層→隠れ層1→(Dropout層)→隠れ層2→(Dropout層)→出力層」のニューラルネットワーク型のディープラーニングのモデルを構築していきます。

  • 入力層のユニット数：4（説明変数Xの数）
  • 隠れ層1のユニット数：12
  • 隠れ層2のユニット数：7
  • 出力層のユニット数：3（目的変数yは1つだが、3カテゴリーあるため）

各層の活性化関数（activation）は……

  • 隠れ層1：selu（Scaled Exponential Linear Unit）
  • 隠れ層2：relu（REctified Linear Unit）
  • 出力層：softmax

Dropout層のドロップアウト率は……

  • Dropout層（隠れ層1と隠れ層2の間）：40%ドロップアウト
  • Dropout層（隠れ層2と出力層の間）：20%ドロップアウト

以下、コードです。

# モデル構築
## モデル定義
model <- keras_model_sequential() 
model %>%
  #隠れ層1
  layer_dense(units = 12, 
              activation = 'selu', 
              input_shape = c(4)) %>%
  #Dropout層（隠れ層1と隠れ層2の間）
  layer_dropout(rate=0.4)  %>%
  #隠れ層2
  layer_dense(units = 7, 
              activation = 'relu')  %>%
  #Dropout層（隠れ層2と出力層の間）
  layer_dropout(rate=0.2)  %>%
  #出力層
  layer_dense(units = 3, 
              activation = 'softmax') 

summary(model) #確認用

 

以下、実行結果です。

 

定義通りになっているのか確認しておきましょう。

  • 入力層→隠れ層1のパラメータ：(4+1)×12=60
  • 隠れ層1→出力層2のパラメータ：(12+1)×7=91
  • 隠れ層2→出力層のパラメータ：(7+1)×3=24

 

次に、コンパイルし学習します。

以下、コードです。

## コンパイル
model %>% compile(loss = 'categorical_crossentropy',
                  optimizer = 'adam',
                  metrics = 'accuracy')

## 学習
history <- 
  model %>% fit(X_train, 
                y_train_d, 
                epochs = 100,
                batch_size = 10, 
                validation_split = 0.25)

history #確認用

 

以下、実行中の画像です。

 

以下、実行結果です。

 

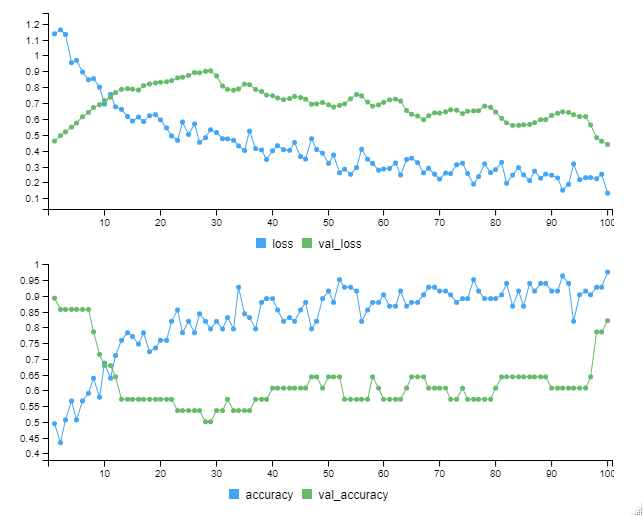
今回学習したモデルの学習データセットの正答率は……

  • train dataの正答率（accuracy）：97.59%
  • validation dataの正答率（val_accuracy）：82.14%

 

モデル③：検証（テストデータ利用）

モデルが構築できたので、テストデータを使い予測し検証していきたいと思います。

先ず、テストデータの説明変数X（特徴量）を使い、目的変数yを予測します。

以下、コードです。

# 予測（検証）
## テストデータの予測
pred_y_test <- 
  model %>% 
  predict_classes(X_test)

 

どのくらいの精度で当てられたのか、混同行列（実測値と予測値の集計表）を使い見ていきます。

以下、コードです。

## 混同行列
table(y_test, pred_y_test)

 

以下、実行結果です。

 

いい感じで予測できていることが分かります。

では、どのくらい正解したのか、正答率を計算してみます。

以下、コードです。

## 正答率
model %>% 
  evaluate(X_test, y_test_d)

 

以下、実行結果です。

 

正答率は94.87%でした。

 

モデル③：コード全体（モデル構築から検証まで）

#
# モデル3
#

# モデル構築
## モデル定義
model <- keras_model_sequential() 
model %>%
  #隠れ層1
  layer_dense(units = 12, 
              activation = 'selu', 
              input_shape = c(4)) %>%
  #Dropout層（隠れ層1と隠れ層2の間）
  layer_dropout(rate=0.4)  %>%
  #隠れ層2
  layer_dense(units = 7, 
              activation = 'relu')  %>%
  #Dropout層（隠れ層2と出力層の間）
  layer_dropout(rate=0.2)  %>%
  #出力層
  layer_dense(units = 3, 
              activation = 'softmax') 

summary(model) #確認用

## コンパイル
model %>% compile(loss = 'categorical_crossentropy',
                  optimizer = 'adam',
                  metrics = 'accuracy')

## 学習
history <- 
  model %>% fit(X_train, 
                y_train_d, 
                epochs = 100,
                batch_size = 10, 
                validation_split = 0.25)

history #確認用

# 予測（検証）
## テストデータの予測
pred_y_test <- 
  model %>% 
  predict_classes(X_test)
## 混同行列
table(y_test, pred_y_test)
## 正答率
model %>% 
  evaluate(X_test, y_test_d)

 

次回

今回は、分類問題でした。次回は、回帰問題です。

RStudio(R)×Keras(TensorFlow)によるお手軽ディープラーニングその2（回帰問題）