
データを集めたら、次にデータを分析しなければなりません。
集めたデータと分析の関係は、食材と料理の関係に似ています。良い食材であっても料理人の腕に問題があると台無しになることがあります。不十分な食材でも調理しだいで美味しくなることもあります。
データの分析の考え方と最も基本的な手法について、全15回にわたってお話しいたします。
- その1 定量分析と定性分析
- その2 分析の基本は比較
- その3 古くて新しいQC7つ道具 ※5回に分けてお話し
- その3-1 QC7つ道具の概要
- その3-2 ヒストグラム・管理図・散布図
- その3-3 散布図+α(相関・回帰線)の話題 ⇒ 今回
- その3-4 パレート図・特性要因図
- その3-5 チェックシート・層別
- その4 古くて新しい新QC7つ道具 ※5回に分けてお話し
- その5 要因分析と統計的因果推論 ※3回に分けてお話し
前回は、その3の「古くて新しいQC7つ道具」のその3-2の「ヒストグラム・管理図・散布図」についてお話ししました。
今回は、その3-3の「散布図+α(相関・回帰線)の話題」です。
散布図
簡単に前回の復習です。
散布図は2つの定量データの関係を把握するときに利用します。
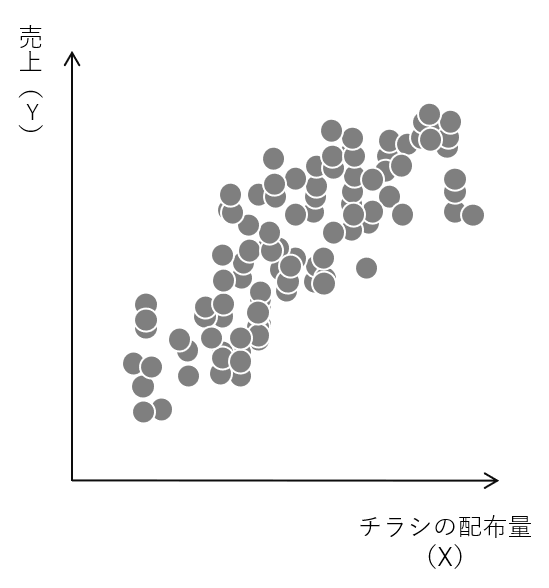
散布図を描くとき、併せて相関係数などの統計学的な指標を計算します。
相関係数は-1から+1の間の数値をとり……
- -1に近いほど「負の相関関係がある」(一方が増加しているにもかかわらず他方が減少する傾向にある場合)
- 0は無相関(正の相関関係も負の相関関係もない)
- +1に近いほど「正の相関関係がある」(一方が増加すると他方も増加する傾向にある場合)
相関関係は、あくまでもデータ上の関係(厳密には線形的な関係)で、このような関係性が本当にあるのかは分かりませんし、そもそも因果関係ではありません。データからこのような関係が読み取れるということに過ぎません。
散布図と回帰直線(単回帰)
散布図を見て頂くと、何となく傾向線と言うか直線のようなものが引けそうな気がします。
その直線を回帰直線(単回帰)と言います。
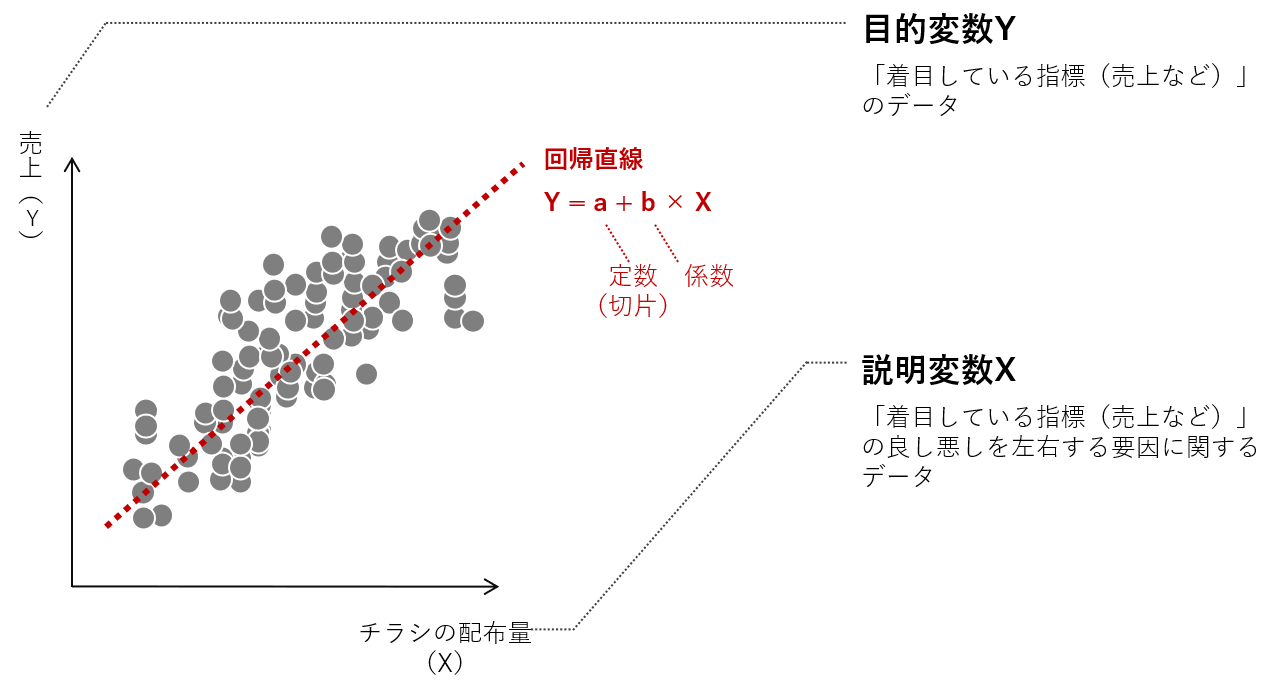
この例ですと……
- ヨコ軸:チラシの配布量(説明変数X)
- タテ軸:売上(目的変数Y)
チラシの配布量が多いほど売上が伸びる、という関係性を表しています。
この例のように、単回帰モデル式(Y=a+bX)を作ることができます。
回帰係数(回帰直線の係数)
相関係数との関係はどうなっているのでしょうか?
- 相関係数が-1に近い:回帰直線の係数bは負の値
- 相関係数が0に近い:回帰直線の係数bは0前後
- 相関係数が+1に近い:回帰直線の係数bは正の値
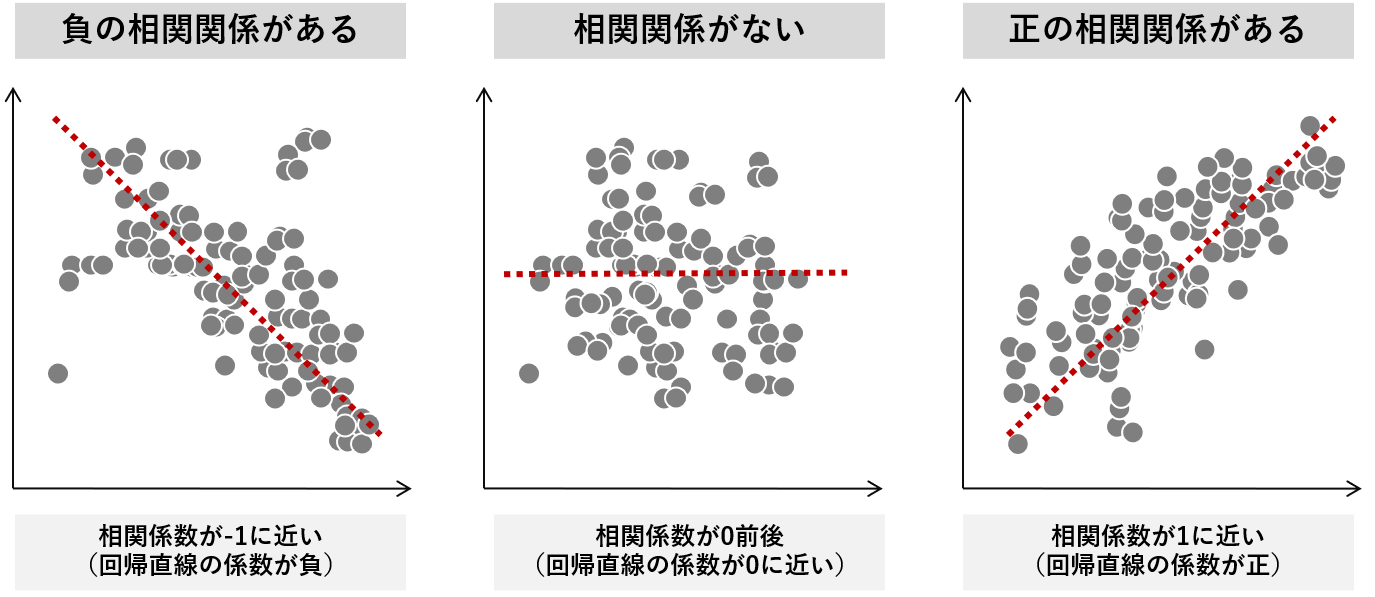
相関係数と回帰直線の係数は、このような関係性を有しています。
ちなみに、回帰係数が0でないかどうかを統計的仮説検定することで「データ同士の関係性の検討」を実施することができます。

単回帰と重回帰
説明変数Xは1変量である必要はありません。多変量でも構いません。伝統的に、1変量なのか多変量なのかで呼び名が変わります。
- 単回帰:説明変数Xが1つ
- 重回帰:説明変数Xが2つ以上

単回帰モデル式も重回帰モデル式も、Excelで簡単に求めることができます。
次回

今回は、その3の「古くて新しいQC7つ道具」のその3-3の「散布図+α(相関・回帰線)の話題」のお話しをしました。
- その1 定量分析と定性分析
- その2 分析の基本は比較
- その3 古くて新しいQC7つ道具 ※5回に分けてお話し
- その3-1 QC7つ道具の概要
- その3-2 ヒストグラム・管理図・散布図
- その3-3 散布図+α(相関・回帰線)の話題
- その3-4 パレート図・特性要因図 ⇒ 次回
- その3-5 チェックシート・層別
- その4 古くて新しい新QC7つ道具 ※5回に分けてお話し
- その5 要因分析と統計的因果推論 ※3回に分けてお話し
次回は、その3-4の「パレート図・特性要因図」です。
もっと知りたい方はこちら
 |
14のフレームワークで考える かんき出版 (2014/9/18) |


