
データを集めたら、次にデータを分析しなければなりません。
集めたデータと分析の関係は、食材と料理の関係に似ています。良い食材であっても料理人の腕に問題があると台無しになることがあります。不十分な食材でも調理しだいで美味しくなることもあります。
データの分析の考え方と最も基本的な手法について、全15回にわたってお話しいたします。
- その1 定量分析と定性分析
- その2 分析の基本は比較
- その3 古くて新しいQC7つ道具 ※5回に分けてお話し
- その4 古くて新しい新QC7つ道具 ※5回に分けてお話し
- その4-1 新QC7つ道具の概要
- その4-2 親和図法(KJ法)とDEMATEL
- その4-3 系統図法(ロジックツリー)
- その4-4 一対比較法とAHP ⇒ 今回
- その4-5 マトリックスデータ解析法と多変量解析
- その5 要因分析と統計的因果推論 ※3回に分けてお話し
前回は、その4の「古くて新しい新QC7つ道具」のその4-3の「系統図法(ロジックツリー)」についてお話ししました。
今回は、その4の「古くて新しい新QC7つ道具」のその4-4の「一対比較法とAHP」です。
Contents
ストレートな数値表現が難しい場合には
一対比較やAHPで評価する
今回紹介する一対比較法とAHP(Analytic Hierarchy Process、階層的意思決定法)は、新QC7つ道具には含まれませんが、よく使われる定性分析手法です。
AHPとは、意思決定手法(複数の選択候補の中から1つ選ぶ)の一つで、評価基準が複数ある場合や評価基準が階層化されているときに利用します。
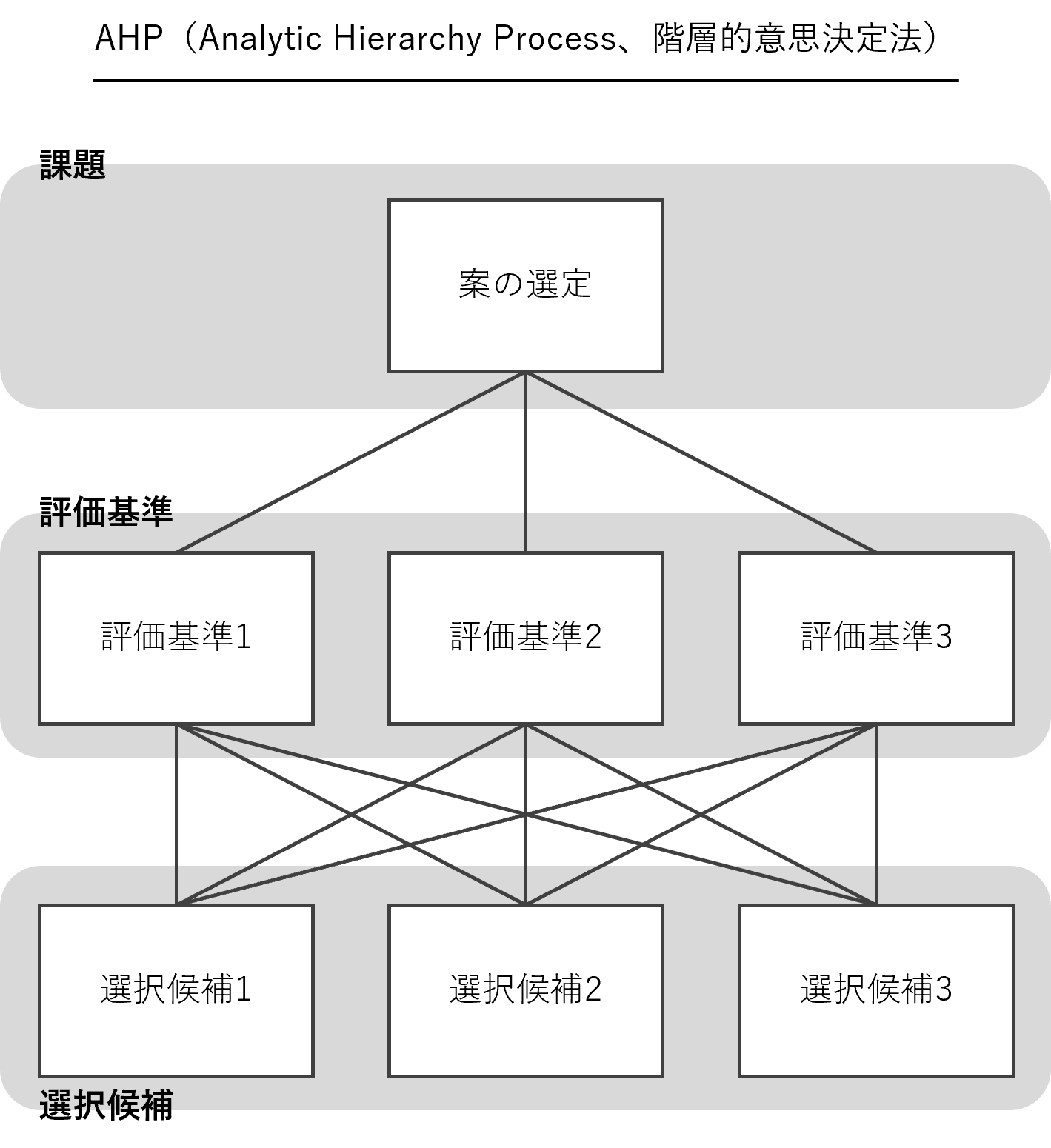
人の感覚を用いた一対比較法を活用し評価していくため、定量化されていない場合にも有効です。人の感覚値を意思決定に反映できるという特徴があります。
一対比較法
先ず、一対比較法について説明します。
流れはシンプルです。
- 先ず、表側と表頭に選択肢を並べた表に、評価結果を記載する
- 次に、相乗平均を計算しスコアを計算する
相乗平均とは、通常の平均である相加平均(算術平均)とは違う平均です。注意しましょう。
ちなみに、Excelなどを使い簡単にスコア計算まで出来ます。
一対比較の評価例
事例の状況設定
今、ある企業内にデータで解決すべきテーマ候補(データサイエンスや機械学習、データ分析などで解決すべき企業内のテーマ候補)が複数あるとします。
以下の2つの評価基準で、テーマを選ぶことにしました。
- インパクトの大きさ
- 容易性
理想は、容易でインパクトの大きなテーマです。
そのためには、各テーマ候補のインパクトの大きさを評価する必要があります。
各テーマ候補のインパクトの大きさを定量的(例:金額換算)できるのであれば、問題ありませんが、そうでない場合も少なくないでしょう。
今、定量的にインパクトの大きさが評価できないとします。
ということで、一対比較法を使い「インパクトの大きさ」を評価する例を説明します。
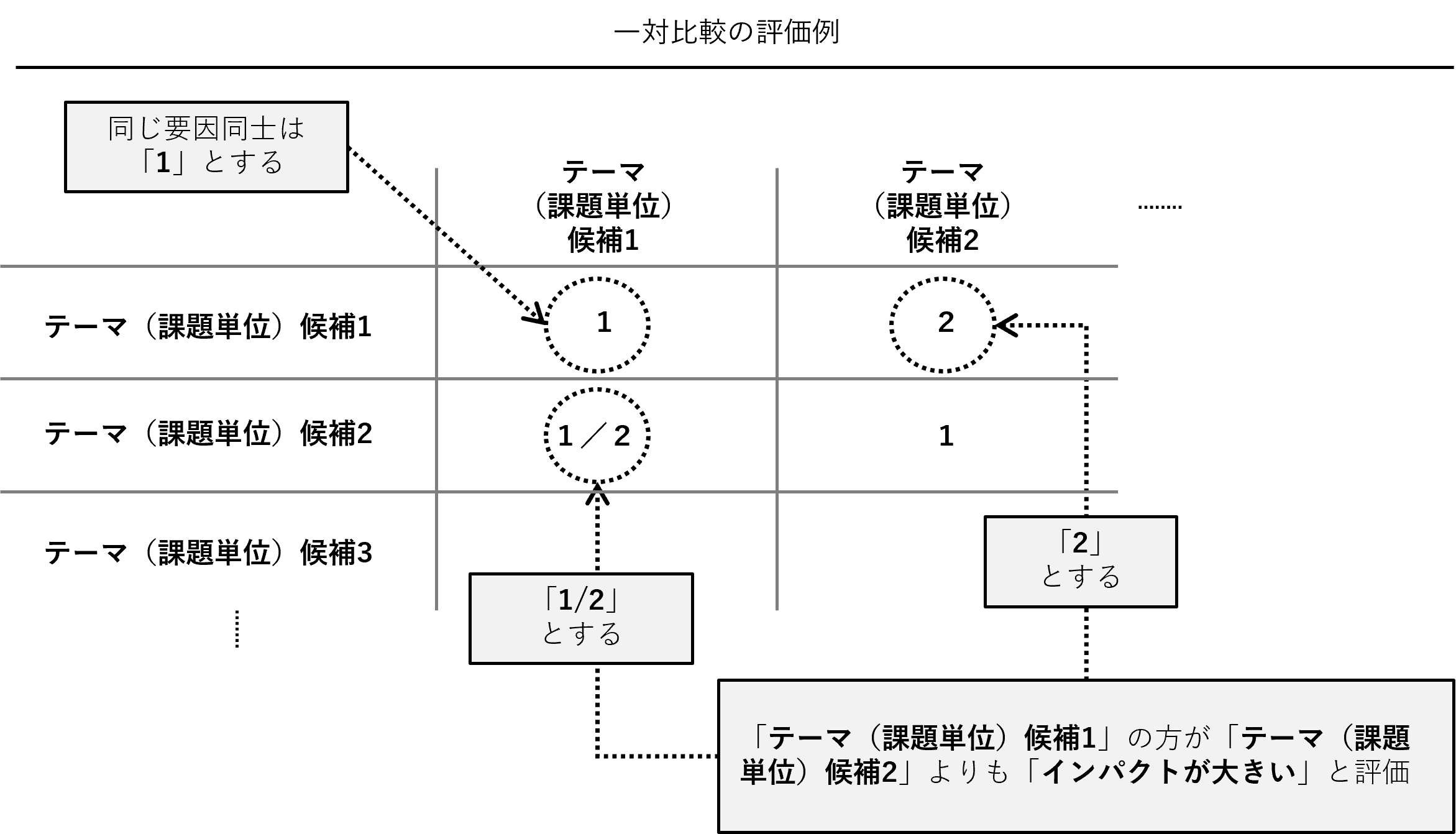
一対比較法で「インパクトの大きさ」を評価する
例えば……
- 「テーマ候補1」の方が「テーマ候補2」よりも「インパクトが大きい」のであれば「2」を……
- 「テーマ候補1」の方が「テーマ候補2」よりも「インパクトが小さい」のであれば「1/2」を……
- 「テーマ候補1」と「テーマ候補2」の「インパクトが同程度」であれば「1」を……
……入力します。この表の対角線はすべて「1」にします。自分自身同士を比較評価しているからです。
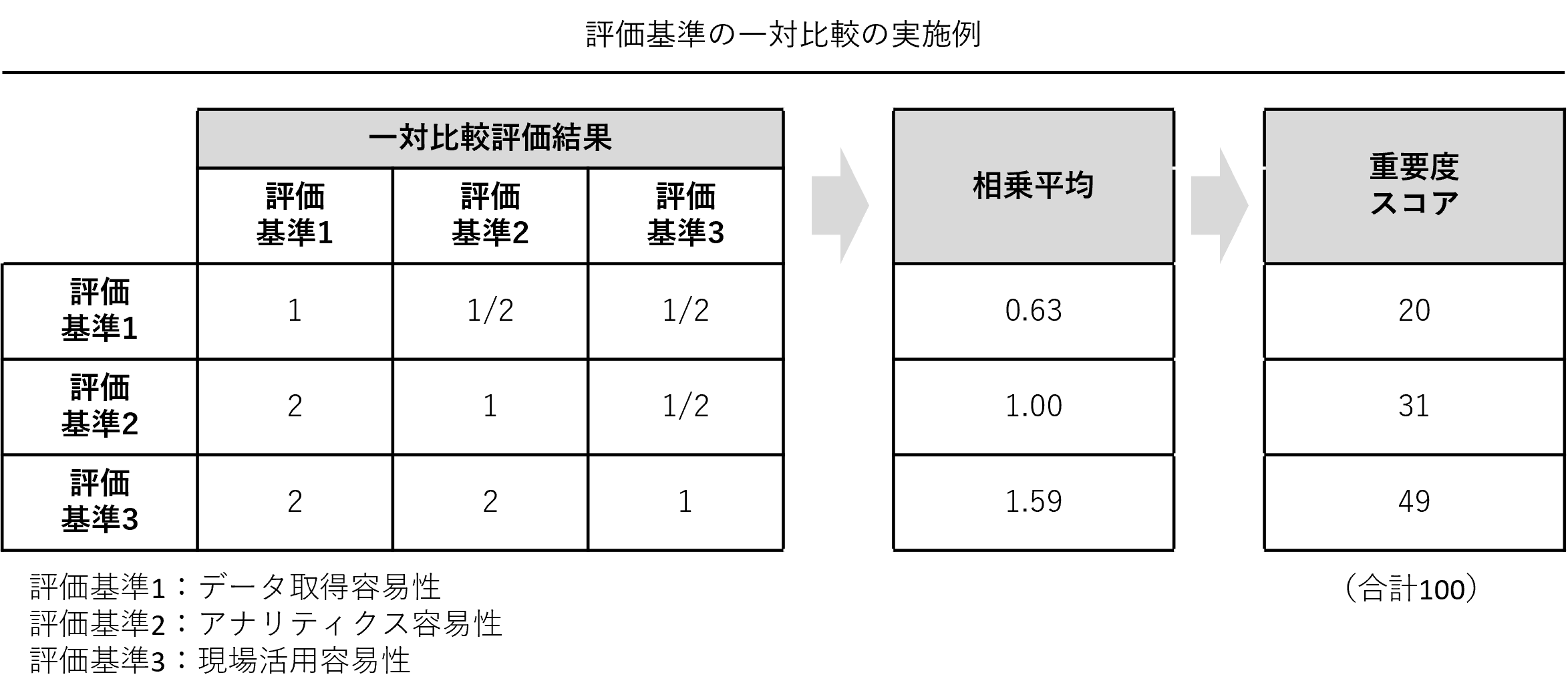
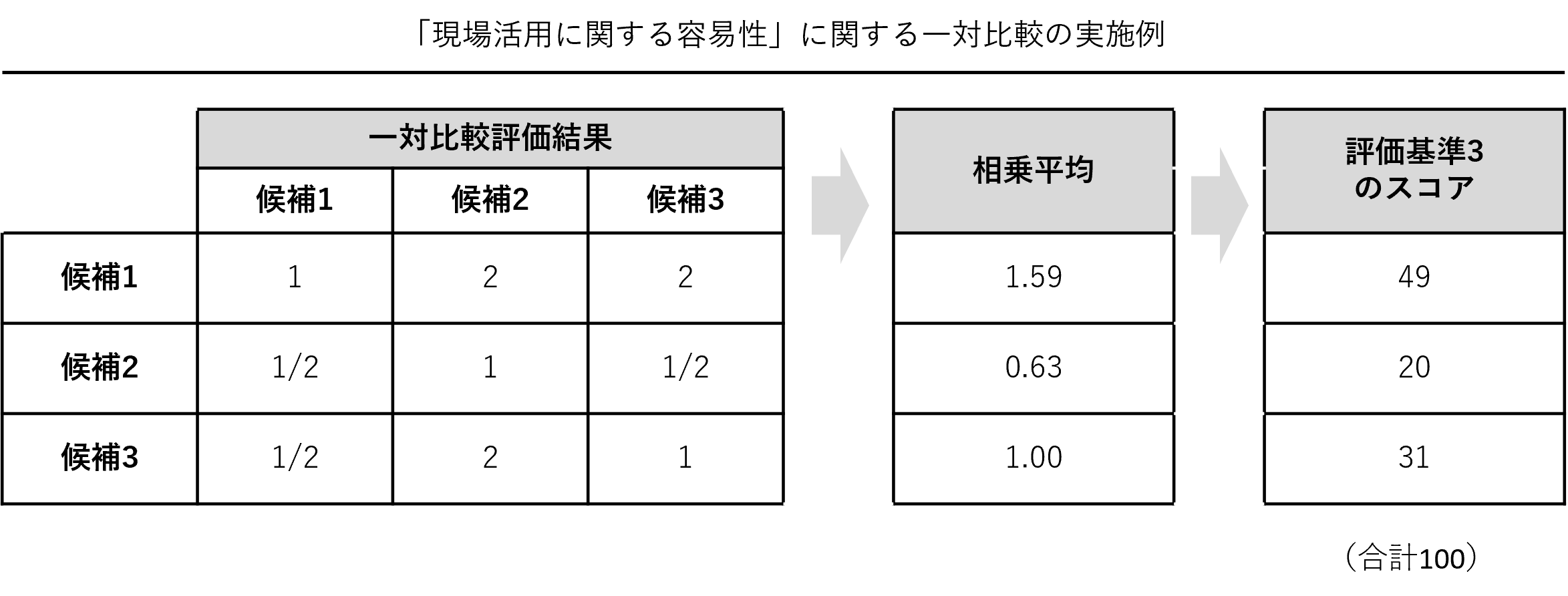
各テーマ候補のインパクトに関するスコアは、各行の相乗平均を計算し、各行の相乗平均の合計値が100になるように調整し求めます。
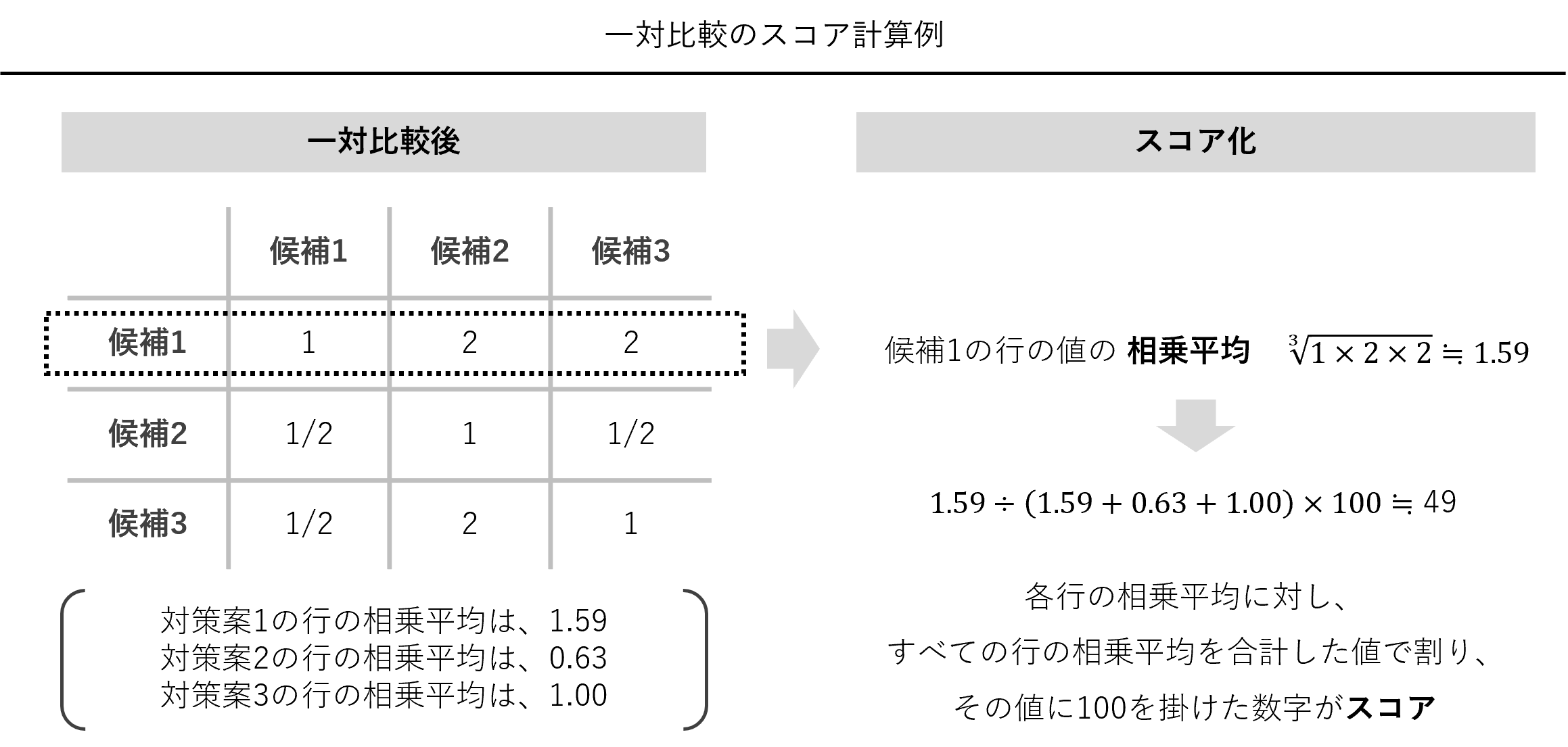
Excelで相乗平均を計算するときは、次の例の場合には「(1×2×2)^(1/3)」となります。
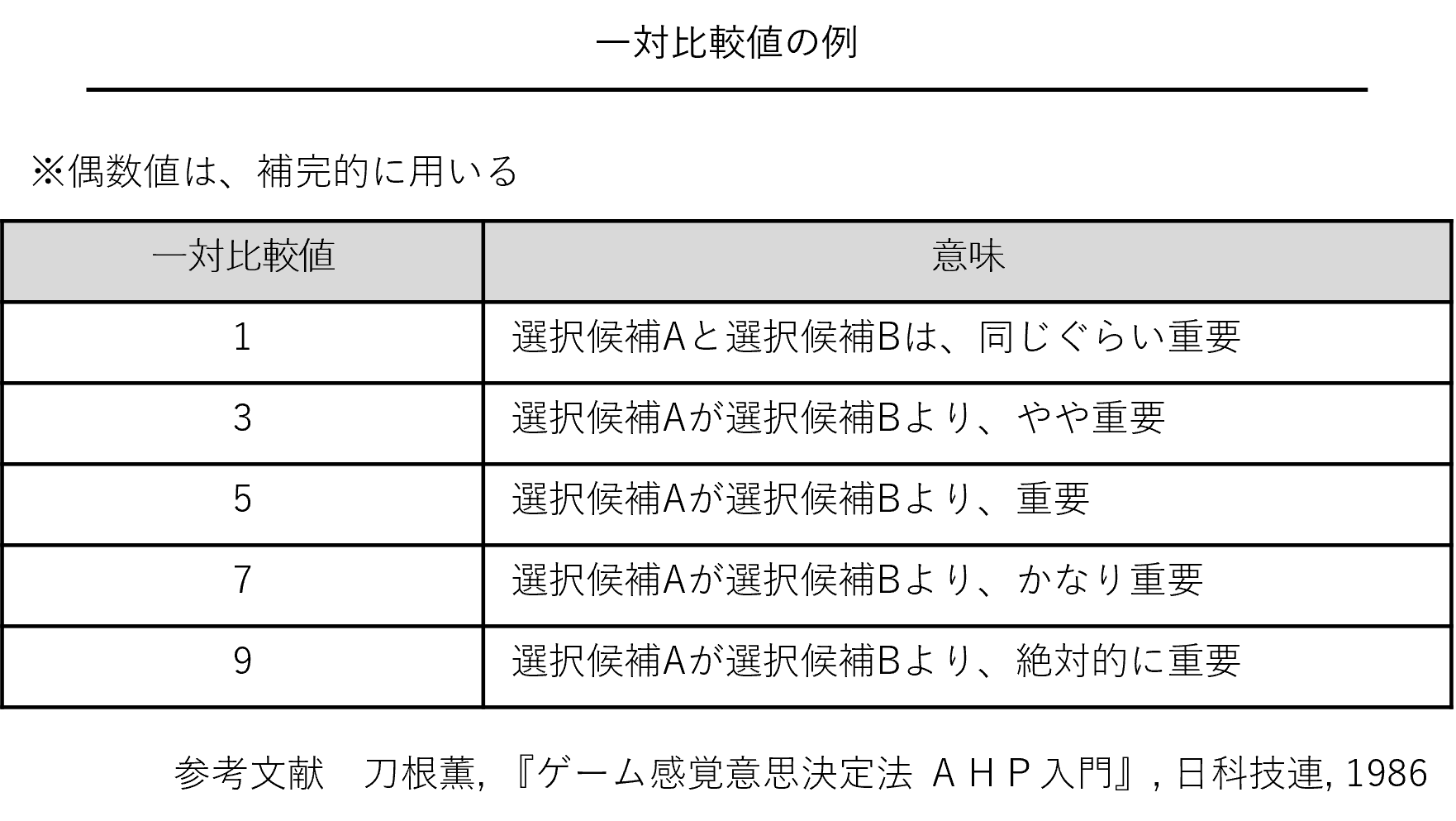
一対比較の評価値は「2」でなくてもいい
「2」を一対比較値として用いましたが、例えば次のようにランクを細かくしてもいいでしょう。
AHP(Analytic Hierarchy Process、階層的意思決定法)
次に、評価基準が複数ある場合に利用するAHPについて説明します。
事例の状況設定
一対比較法と同じ事例を使います。
復習です。
ある企業内にデータで解決すべきテーマ候補(データサイエンスや機械学習、データ分析などで解決すべき企業内のテーマ候補が複数あり、以下の2つの評価基準で、テーマを選ぶことにしました。
- インパクトの大きさ
- 容易性
理想は、容易でインパクトの大きなテーマです。
「容易性」は、さらに以下の3つの評価基準に細分化されます。
- データ取得に関する容易性
- アナリティクスに関する容易性
- 現場活用に関する容易性
このようなとき、AHPを使います。
AHPの簡易手順
AHPの簡易手順は、次にようになります。
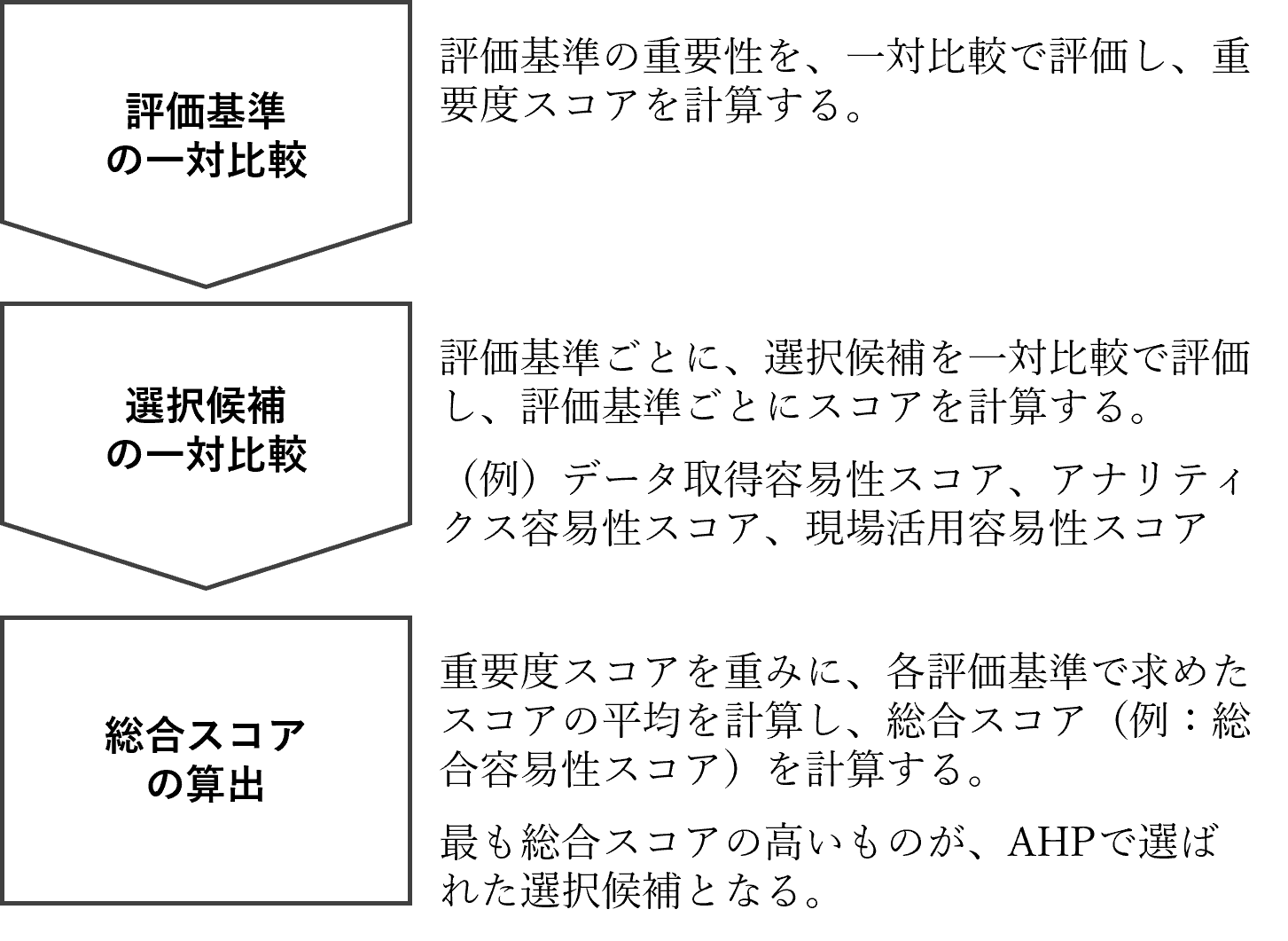
AHPで「容易性」を評価する
先ずは、評価基準の一対比較です。
「データ取得に関する容易性」「アナリティクスに関する容易性」「現場活用に関する容易性」の3つの評価基準の重要性を評価します。どの評価基準がより重要かを一対比較評価し重要度スコアを求めます。
次に、選択候補の一対比較です。
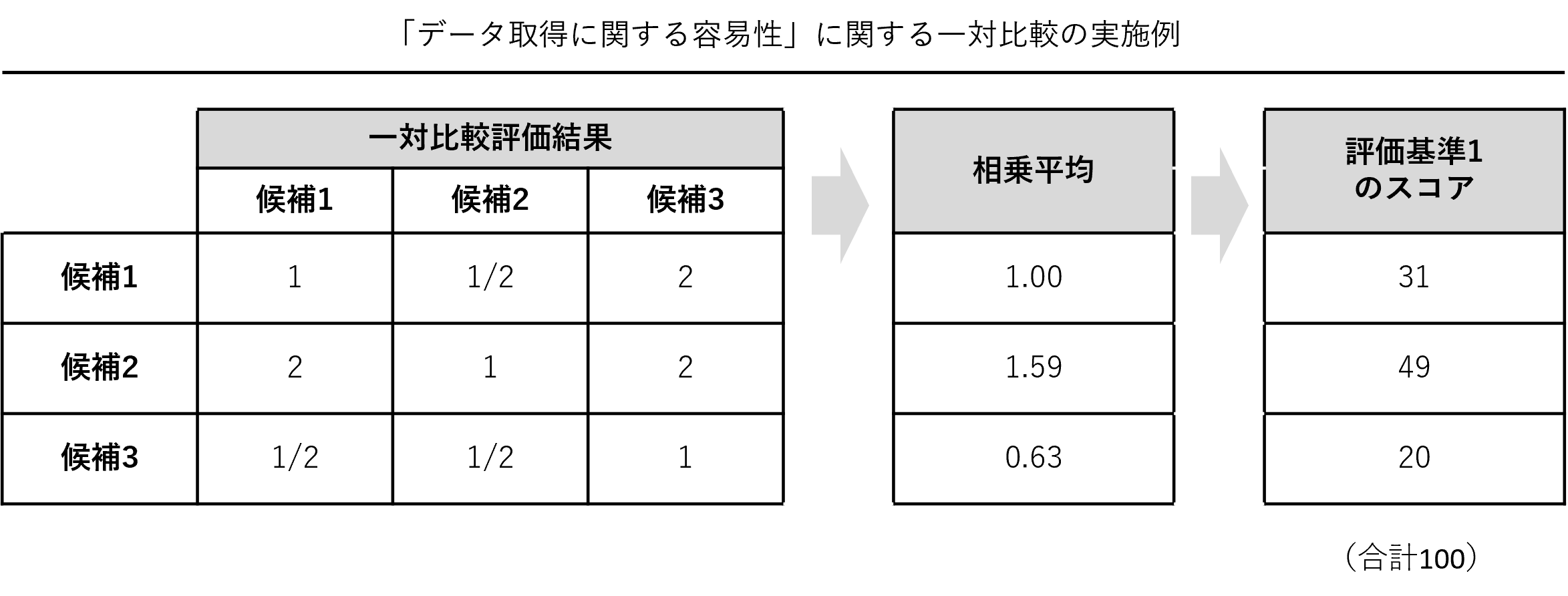
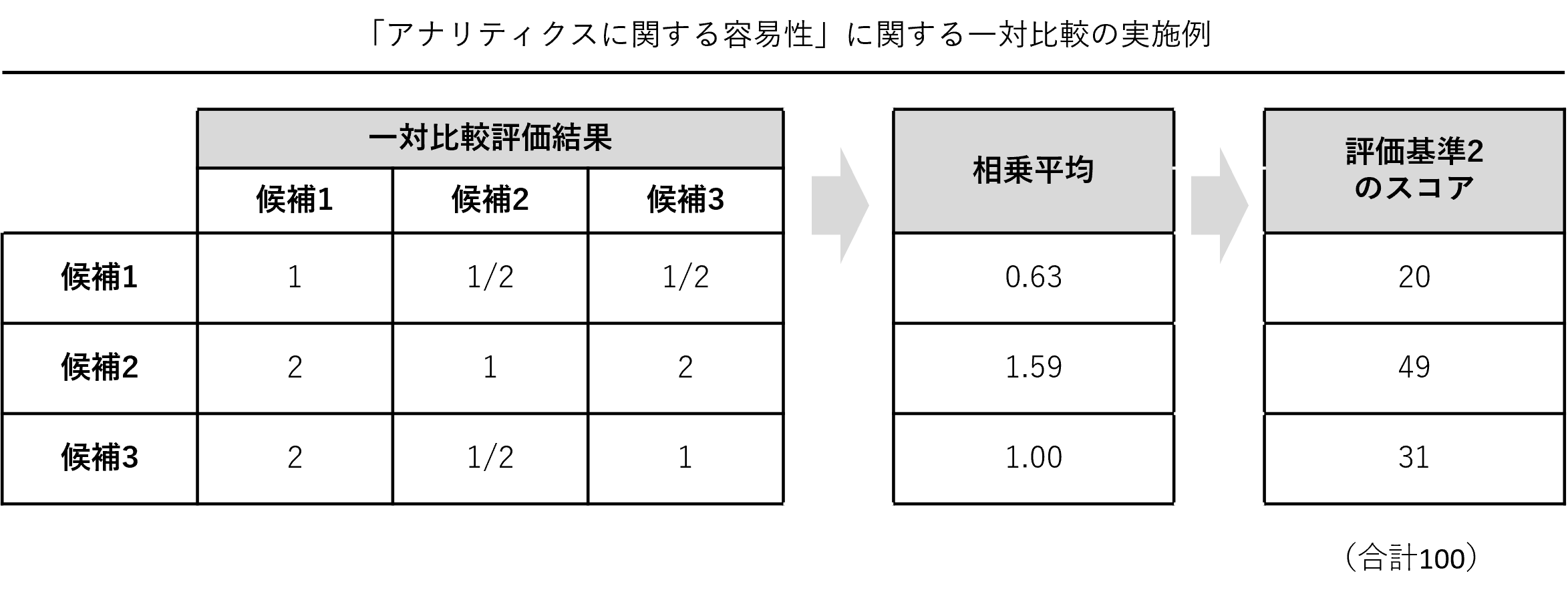
「データ取得に関する容易性」「アナリティクスに関する容易性」「現場活用に関する容易性」のそれぞれの評価基準ごとに、テーマ候補同士を一対比較評価しそれぞれの容易性スコアを求めます。3つの容易性スコアが算出されます。
以下、「データ取得に関する容易性」に関する一対比較の実施例です。
以下、「アナリティクスに関する容易性」に関する一対比較の実施例です。
以下、「現場活用に関する容易性」に関する一対比較の実施例です。
重要度スコアと各評価基準で求めた3つの容易性スコアを用い、総合スコアを算出します。
求め方は簡単で、重要度スコアを重みに、各評価基準で求めた3つの容易性スコアの平均を計算します。この平均は、通常の相和平均(算術平均)になります。
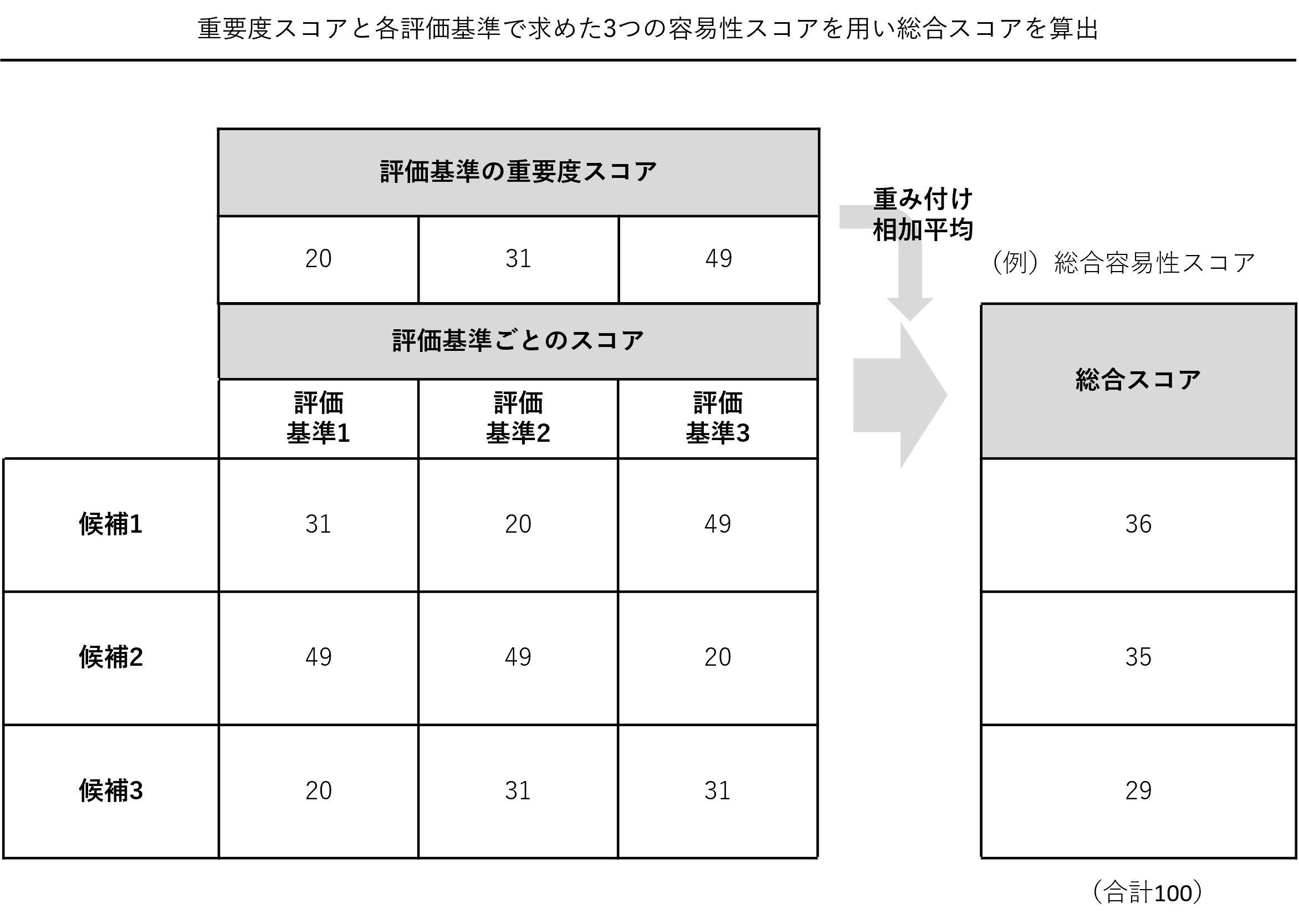
例の「候補1」の場合、「36≒31×20/100+20×31/100+49×49/100」となります。
次回

今回は、その4の「古くて新しい新QC7つ道具」のその4-4の「一対比較法とAHP」のお話しをしました。
- その1 定量分析と定性分析
- その2 分析の基本は比較
- その3 古くて新しいQC7つ道具 ※5回に分けてお話し
- その4 古くて新しい新QC7つ道具 ※5回に分けてお話し
- その4-1 新QC7つ道具の概要
- その4-2 親和図法(KJ法)とDEMATEL
- その4-3 系統図法(ロジックツリー)
- その4-4 一対比較法とAHP
- その4-5 マトリックスデータ解析法と多変量解析 ⇒ 次回
- その5 要因分析と統計的因果推論 ※3回に分けてお話し
次回は、その4-5の「マトリックスデータ解析法と多変量解析」のお話しをします。
もっと知りたい方はこちら
 |
14のフレームワークで考える かんき出版 (2014/9/18) |

