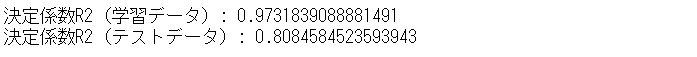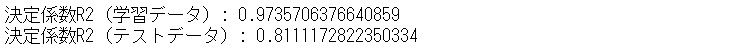色々な特徴量選択(feature selection)の方法があります。
よくあるやり方としては……
- 分散や共分散を元に特徴量(説明変数)を削る方法
- モデルへの影響を考慮しながら特徴量(説明変数)を削る方法
……などなど。
モデルへの影響を考慮しながら特徴量(説明変数)を削る方法は、「RFE法」(Recursive Feature Elimination)と呼ばれています。1つづつ削れば、ステップワイズ法となります。
Pythonでよく使われる機械学習のパッケージであるScikit-Learn(sklearn)にも、「RFE法」(Recursive Feature Elimination)が実装されています。
と言うことで、今回は「Python Scikit-Learn(sklearn)を使ったステップワイズな特徴量選択(変数選択)RFE」というお話しというか、やり方について簡単に説明します。
ちなみに、PythonにScikit-Learn(sklearn)をインストールされていない方は、インストールしておいてください。
Contents [hide]
ステップワイズな変数選択法RFEとは?
RFEで、モデルへの影響を考慮しながら特徴量(説明変数)を1つづつ削る、特徴量選択(変数選択)をすることができます。
モデルとは、目的変数yと特徴量(説明変数)Xからなる予測モデルです。
では、簡単に説明します。
予測モデルを何かしらのアルゴリズムで構築すると、各特徴量に対し重みのようなものが出力されます。
重回帰モデルであれば標準偏回帰係数、ランダムフォレストであればインポータンスなど。
標準偏回帰係数(もしくは、インポータンス)が、ほぼ0な特徴量を1つ選び除外します。ほぼ0な特徴量は、目的変数yの予測に大きな影響を与えないからです。要は、あまり精度悪化させないからです。
残った特徴量で、再度、予測モデルを構築。各特徴量に対し標準偏回帰係数(もしくは、インポータンス)を出力させ、ほぼ0な特徴量を1つ選び除外します。
これを繰り返します。
今回利用するデータ
2つのデータセットを使います。
- 分類問題:乳がんの診断のデータセット
- 回帰問題:カリフォルニアの住宅価格のデータセット
どちらも、Scikit-Learn(sklearn)から提供されているサンプルデータセットです。
データセットの簡単な説明を以下でしています。
AutoML【TPOT】で分類問題を解く‐乳がんの診断のデータセット
https://www.salesanalytics.co.jp/software/automl/automl003/#iAutoML【TPOT】で回帰問題を解く‐カリフォルニアの住宅価格のデータセット
https://www.salesanalytics.co.jp/software/automl/automl004/#i
乳がんの診断のデータセットの目的変数は、良性(=1)と悪性(=0)の2クラス値です。
カリフォルニアの住宅価格のデータセットの目的変数は、カリフォルニアの予測したい区画ごとの住宅価格の中央値です。
流れ
それぞれのデータセットに対し、以下のような流れで実施していきます。
- 先ず、すべての特徴量を使いモデルを構築します
- 次に、RFECV関数を使って特徴量を削りモデルを構築します
今回構築するモデルは、Scikit-Learn(sklearn)に実装されているランダムフォレストです。
すべての特徴量を使ったモデルと、RFECV関数を使って削った特徴量を使ったモデルで、精度を比較します。
今回の精度指標は以下です。
- 分類問題:正答率(accuracy)
- 回帰問題:決定係数(r2)
分類問題:乳がんの診断
ライブラリーやデータの読み込み、データ分割など
モデルを構築する前に、以下の3つのことを実施します。
- 必要なライブラリーの読み込み
- データセットの読み込み
- データセットの分割(学習データとテストデータ)
以下、コードです。
# 必要なライブラリの読み込み
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import RFECV
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
import pandas as pd
# データセットの読み込み
load_breast_cancer = load_breast_cancer(as_frame=True)
X = load_breast_cancer.data
y = load_breast_cancer.target
# データセットを学習用とテスト用に分割する
X_train, X_test, y_train, y_test = train_test_split(X,
y,
train_size=0.75,
test_size=0.25,
random_state=42)
すべての特徴量を使いモデルを構築
先ず、すべての特徴量を使い学習データでモデルを構築し、構築したモデルをテストデータで検証します。
以下、コードです。
# モデル構築(学習データ)
forest = RandomForestClassifier(class_weight='balanced')
forest.fit(X_train, y_train)
# 検証結果(正答率)
print('正答率(学習データ):',
forest.score(X_train,
y_train))
print('正答率(テストデータ):',
forest.score(X_test,
y_test))
正答率(テストデータ)は、97.90%です。
RFECV関数を使って特徴量を削りモデルを構築
次に、RFECV関数を使って特徴量を削り学習データでモデルを構築し、構築したモデルをテストデータで検証します。
以下、コードです。
# 特徴量選定
rfecv = RFECV(
estimator=RandomForestClassifier(class_weight='balanced'),
n_jobs=-1,
scoring="accuracy",
cv=10,
)
rfecv.fit(X_train, y_train)
選択した特徴量(残った特徴量)の数を見てみます。
以下、コードです。
# 選択した特徴量の数 rfecv.n_features_
以下、実行結果です。
30個あった特徴量が、半分以下の14個まで減りました。
どの特徴量を選択したのか(残ったのか)を見てみます。
以下、コードです。
# 選択した特徴量 X_train.columns[rfecv.support_]
以下、実行結果です。
この選択した(残った)特徴量を使い、学習データでモデルを構築し、構築したモデルをテストデータで検証します。
以下、コードです。
# モデル構築(学習データ)
forest = RandomForestClassifier(class_weight='balanced')
forest.fit(rfecv.transform(X_train), y_train)
# 検証結果(正答率)
print('正答率(学習データ):',
forest.score(rfecv.transform(X_train),
y_train))
print('正答率(テストデータ):',
forest.score(rfecv.transform(X_test),
y_test))
メソッド「transform()」を使い、選択した特徴量を抜き出しています。
以下、実行結果です。
正答率(テストデータ)は、97.20%です。
すべての特徴量を使ったとき正答率(テストデータ)が97.90%だったので、それほど悪化していないことが分かります。
回帰問題:カリフォルニアの住宅価格
ライブラリーやデータの読み込み、データ分割など
モデルを構築する前に、以下の3つのことを実施します。
- 必要なライブラリーの読み込み
- データセットの読み込み
- データセットの分割(学習データとテストデータ)
以下、コードです。
# 必要なライブラリの読み込み
from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
import pandas as pd
# データセットの読み込み
california_housing = fetch_california_housing(as_frame=True)
X = california_housing.data
y = california_housing.target
# データセットを学習用と検証用に分割する
X_train, X_test, y_train, y_test = train_test_split(X,
y,
train_size=0.75,
test_size=0.25,
random_state=42)
すべての特徴量を使いモデルを構築
先ず、すべての特徴量を使い学習データでモデルを構築し、構築したモデルをテストデータで検証します。
以下、コードです。
# モデル構築(学習データ)
forest = RandomForestRegressor()
forest.fit(X_train, y_train)
# 検証結果(決定係数R2)
print('決定係数R2(学習データ):',
forest.score(X_train,
y_train))
print('決定係数R2(テストデータ):',
forest.score(X_test,
y_test))
以下、実行結果です。
決定係数R2(テストデータ)は、80.85%です。
RFECV関数を使って特徴量を削りモデルを構築
次に、RFECV関数を使って特徴量を削り学習データでモデルを構築し、構築したモデルをテストデータで検証します。
以下、コードです。
# 特徴量選定
rfecv = RFECV(
estimator=RandomForestRegressor(),
n_jobs=-1,
scoring="r2",
cv=10,
)
rfecv.fit(X_train, y_train)
選択した特徴量(残った特徴量)の数を見てみます。
以下、コードです。
# 選択した特徴量の数 rfecv.n_features_
以下、実行結果です。
8個あった特徴量が、6個まで減りました。
どの特徴量を選択したのか(残ったのか)を見てみます。
以下、コードです。
# 選択した特徴量 X_train.columns[rfecv.support_]
以下、実行結果です。
この選択した(残った)特徴量を使い、学習データでモデルを構築し、構築したモデルをテストデータで検証します。
以下、コードです。
# モデル構築(学習データ)
forest = RandomForestRegressor()
forest.fit(rfecv.transform(X_train), y_train)
# 検証結果(決定係数R2)
print('決定係数R2(学習データ):',
forest.score(rfecv.transform(X_train),
y_train))
print('決定係数R2(テストデータ):',
forest.score(rfecv.transform(X_test),
y_test))
メソッド「transform()」を使い、選択した特徴量を抜き出しています。
以下、実行結果です。
決定係数R2(テストデータ)は、81.11%です。
すべての特徴量を使ったとき決定係数R2(テストデータ)が80.85%だったので、悪化しているどころか良くなっています。
まとめ
今回は「Python Scikit-Learn(sklearn)を使ったステップワイズな特徴量選択(変数選択)RFE」というお話しをしました。
Scikit-Learn(sklearn)の機能だけでも、ステップワイズな特徴量選択が可能です。
実は、Pythonには「特徴量エンジニアリング専用のパッケージ」も色々あります。もっと高度な特徴量選択を実施したい方は、それらのパッケージを使うのもいいでしょう。別の機会にお話しします。