第267話｜顧客であるまでの期間（離反する時期）を予測する生存時間分析

質問です。

あなたの会社の顧客が、顧客である期間はどのくらいですか？
この顧客は何年後に離反しますか？

もう1つ質問です。

あなたの会社の機械（もしくは、顧客の機械）が、1年間正常に稼働した後、どのくらい持ちますか？
この機械はどのくらいで故障しますか？

このようなことは、生存時間分析で予測することができます。

生存時間分析は、対象となるイベント（離反や故障など）をすべて観察することなく、イベント（離反や故障など）までの時間を推測するための統計学的なデータサイエンス技術です。

今回は、「顧客であるまでの期間（離反する時期）を予測する生存時間分析」というお話しをします。

Contents

打ち切りデータの問題
カプラン・マイヤー法（Kaplan-Meier method）
Cox比例ハザードモデル（Cox proportional hazard model）
今回のまとめ

打ち切りデータの問題

顧客の離反や機械の故障などを分析するときの問題の1つとして、打ち切りデータの問題があります。

打ち切りデータの問題とは、最終的な結果（離反や故障など）がわかる前のデータしかないデータです。

例えば、ある時期のデータまでを活用するとき場合、その時期以降のデータがないため、その時期以降に離反した顧客のイベント（この場合、離反）のデータは「打ち切り」となります。

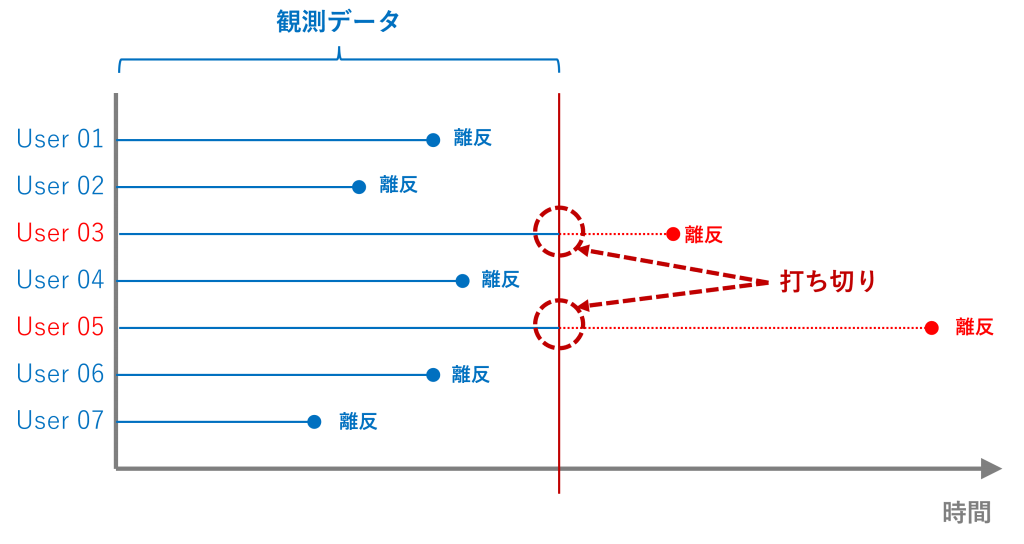
打ち切りデータの問題を解決するには、すべての顧客が離反するまでデータを取得し続けなければなりません。非現実的です。

生存時間分析では、このイベント（例えば、離反や故障）の打ち切りの問題を前提にした技術です。

カプラン・マイヤー法（Kaplan-Meier method）

カプラン・マイヤー法（Kaplan-Meier method）とは、生存時間分析の手法の一つで、生存率曲線（survival curves）を使い、生存時間（顧客である期間）の推定を行います。

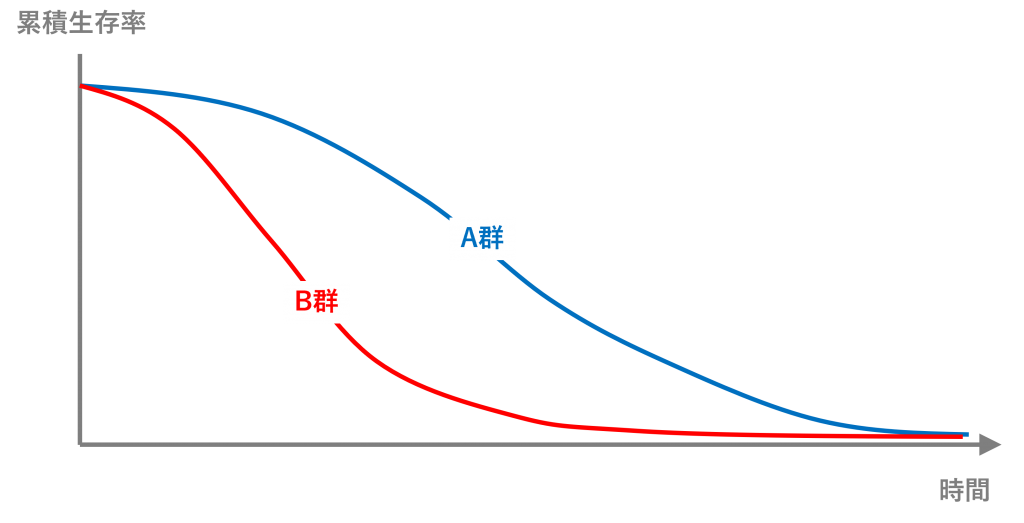
生存率曲線（survival curves）に影響を及ぼす要因（説明変数X）が見つかれば、生存時間（顧客である期間）を伸ばすことができるかもしれません。

そのような分析をするために、Cox比例ハザードモデル（Cox proportional hazard model）を使います。

Cox比例ハザードモデル（Cox proportional hazard model）

Cox比例ハザードモデル（Cox proportional hazard model）とは、離反or継続を予測するロジスティック回帰の概念に、時間的な概念を加味したかのようなモデルです。

時間的な概念を加味したかのようなモデルとは、離反or継続と予測するのではなく、1年以内にどのくらい離反しそうかを予測する、といった感じです。

このCox比例ハザードモデル（Cox proportional hazard model）を使うことで、想定される要因（説明変数X）がどのくらい生存時間に影響を与えているのかを、分析することができます。

言い換えると、何が顧客離反を早めているのかや何が故障をはやめているのかなどを、分析することができます。

ここではハザードや比例ハザードそのものの説明を避けますが、Cox比例ハザードモデル（Cox proportional hazard model）は、説明変数Xは時間で変化せず、比例ハザードは説明変数Xにのみ依存することを前提にしています。要は、比例ハザードは時間で変化せず一定ということです。

Cox比例ハザードモデル（Cox proportional hazard model）の進化版として、時間変化するCox比例ハザードモデルがあります。

さらに、スパースcox回帰モデルやランダム生存時間フォレスト（Random Survival Forest）など機械学習っぽいモデルも色々あります。