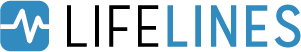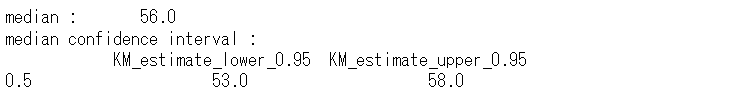生存時間分析とは……
- 生物の死
- 顧客の離反
- 機械システムの故障
……など、あるイベント(例:死、離反、故障など)が発生するまでの時間(期間)を推測するための統計学的なデータサイエンス技術です。
詳細というか概要を以下の記事で説明しています。
第267話|顧客であるまでの期間(離反する時期)を予測する生存時間分析
Pythonで生存時間分析を実施する手段は色々ありますが、生存時間用のライブラリーを活用するのがいいでしょう。今回利用するのは、Lifelinesというライブラリーです。
今回は、Lifelinesというライブラリーの簡単な使い方について説明します。次回、具体的な顧客離反事例を用いて説明します。
Contents [hide]
ライブラリー「Lifelines」のインストール
コマンドプロンプト上で、condaでインストールするときのコードは以下です。
conda install -c conda-forge lifelines
コマンドプロンプト上で、pipでインストールするときのコードは以下です。
pip install lifelines
生存時間分析のデータセットの基本フォーマット
生存時間分析を実施するときの、データセットの型のようなものがあります。最低限必要なのは、以下の2つの変数です。
- 生存時間(例:顧客である期間)
- イベント生起の有無(True or False)
観測期間内にイベント(例:離反)が生起しなかったということは、打ち切られたということです。
さらに、特徴量(説明変数X)を加えることも多いです。生存時間が特徴量(説明変数X)によってどのように変化するのかを分析することができます。
| 顧客ID | 生存時間 | イベント生起 | 性別 | 年齢 | 居住地 |
| 1098378 | 10 | False | F | 34 | Tokyo |
| 8971298 | 3 | True | M | 50 | Saitama |
| 6479816 | 6 | True | M | 27 | Chiba |
| 1796325 | 8 | False | F | 62 | Tokyo |
生存時間分析のモデル
生存時間分析も他の例にもれず……
- パラメトリックなモデル
- セミパラメトリックなモデル
- ノンパラメトリックなモデル
……にざっくり分かれます。
パラメトリックなモデルの代表格が、ワイブル回帰モデルです。何らかの確率分布を仮定するモデルです。
セミパラメトリックなモデルの代表格が、Cox比例ハザードモデル(Cox proportional hazard model)です。確率分布を仮定しないモデルですが、特徴量(説明変数X)を考慮するためセミパラメトリックと言われています。
ノンパラメトリックなモデルの代表格が、カプランマイヤー推定法により求める方法です。確率分布を仮定しないモデルです。基本、特徴量(説明変数X)を考慮しませんが、郡別に求めたりします。
ハザードって何?
ここまでの説明に、ハザードという用語が、何度か登場しています。
生存時間分析をするとき、以下の3つの関数の存在を意識する必要があります。
- ハザード関数 h(t):ある時点t までにイベント(例:離反)が発生していないもとで,次の瞬間にイベント(例:離反)が発生する確率
- 生存関数 S(t):生存時間がt以上となる確率、言い換えると、時刻tまでにイベント(例:離反)が発生していない確率
- 確率密度関数 f(t):生存時間を表す確率変数Tの確率密度関数
ハザード関数 h(t)と生存関数 S(t)、確率密度関数 f(t)は、密接に関係しています。3つの関数の内、2つの関数が分かればもう1つの関数を導き出すことができます。
パラメトリックなモデルの場合、確率密度関数 f(t)に何かしら明示的な確率分布を仮定します。ワイブル分布や指数分布を仮定することが多いです。
ワイブル分布を仮定し特徴量(説明変数X)を加味した場合、ワイブル回帰モデルと言われます。ワイブル分布のパラメータを特徴量(説明変数X)で変化させるモデルです。ここでは扱いません。
ここでは、特定の確率分布を仮定しない、セミパラメトリックなCox比例ハザードモデル(Cox proportional hazard model)を使っていきます。
ちなみに、Lifelinesというライブラリーでは、どちらも実施可能です。パラメトリックなモデルもワイブル分布以外に色々なものが、Lifelinesで実施できます。
ライブラリーのサンプルデータで生存時間分析
生存時間分析がどのようなものなのかの感覚を掴むため、Python の生存時間分析ライブラリー Lifelines のサンプルデータを使って分析してみます。
- その1:ショウジョウバエの生存日数
- その2:回帰モデル用のダミーデータ
- その3:出所後 1 年間追跡調査データ
先ずは、共通して必要なライブラリーを読み込みます。
以下、コードです。
# 必要なライブラリーの読み込み
import pandas as pd
import numpy as np
from lifelines import *
from lifelines.utils import median_survival_times
import matplotlib.pyplot as plt
# グラフのスタイル
plt.style.use('ggplot')
# グラフサイズ設定
plt.rcParams['figure.figsize'] = [12, 9]
生存時間分析ライブラリー Lifelines 以外は、よく使う一般的なPythonのライブラリーです。
その1:ショウジョウバエの生存日数
最もシンプルなデータセットの1つで、「生存日数」(T)と「イベント生起」(E)、「群(miR-137群とコントロール群)」(group)の3変数からなるデータセットです。
カプランマイヤー推定法を使い分析していきます。
先ず、データを読み込みます。以下、コードです。
# データセットの読み込み from lifelines.datasets import load_waltons df = load_waltons() df #確認
以下、実行結果です。
カプランマイヤー推定をします。以下、コードです。
# カプランマイヤー推定 T = df['T'] #生存期間 E = df['E'] #イベント生起 kmf = KaplanMeierFitter() kmf.fit(T, event_observed=E)
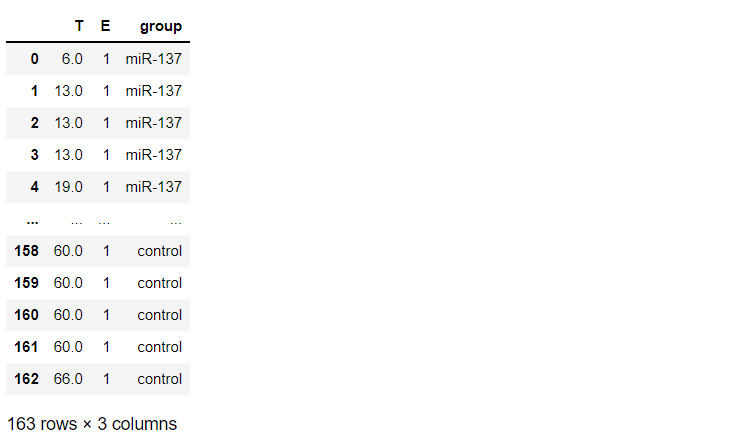
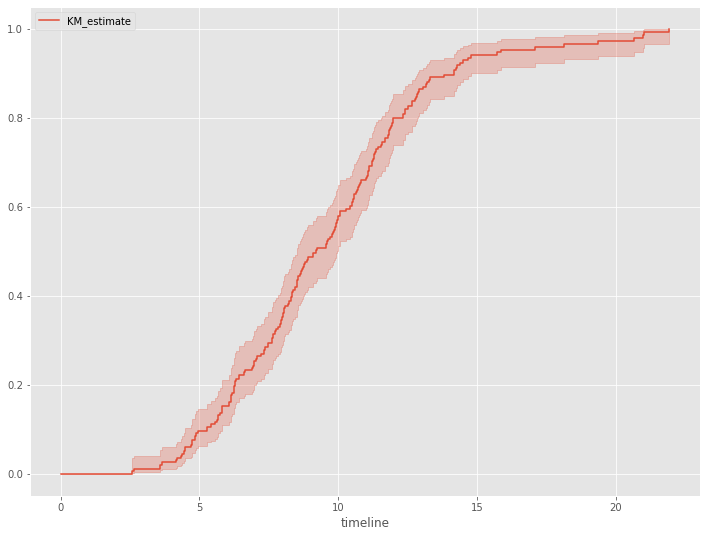
生存時間を表す確率変数Tの確率密度関数の累積確率分布を見てみます。この累積確率分布は、生存時間がt以上とならない確率です。
以下、コードです。
# 累積分布関数 kmf.plot_cumulative_density()
以下、実行結果です。
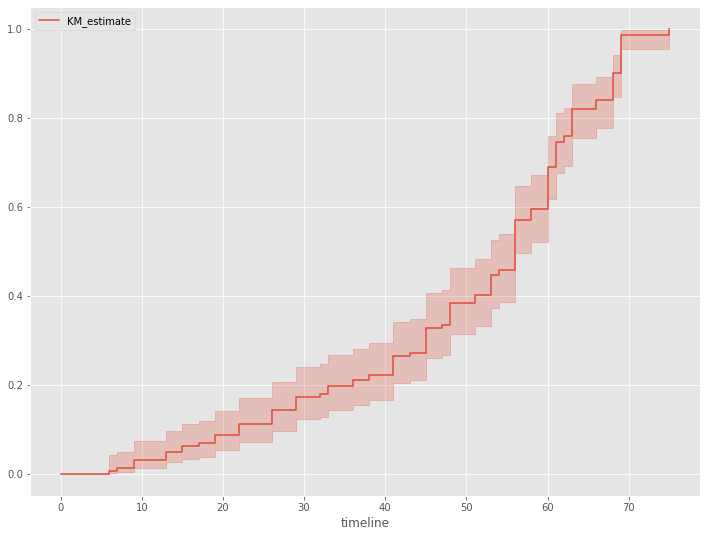
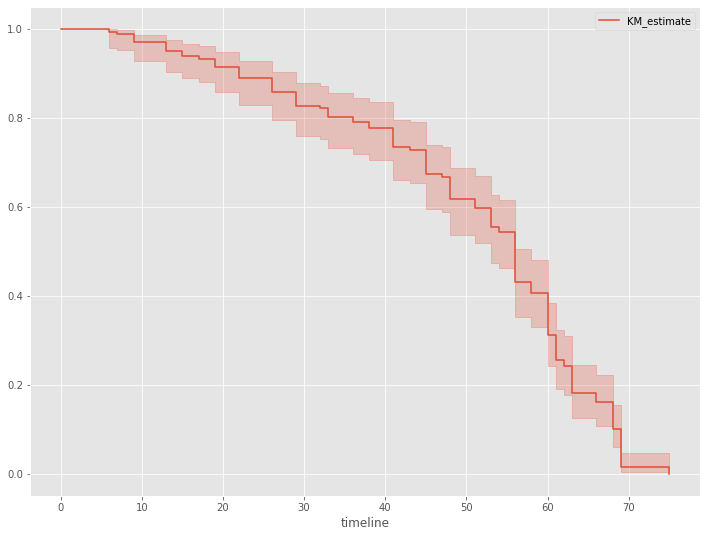
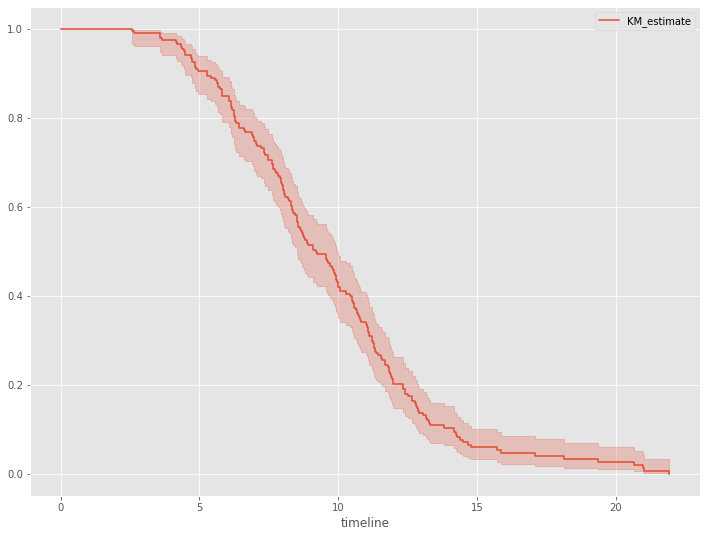
さらに、生存関数を見てみます。生存関数とは、生存時間がt以上となる確率、言い換えると、時刻tまでにイベント(例:離反)が発生していない確率です。
以下、コードです。
# 生存関数 kmf.plot_survival_function()
以下、実行結果です。
死亡時期を推定してみます。平均値ではなく中央値を使います。50%が死亡する時期です。
以下、コードです。
# 推定結果(中央値と信頼区間)
print(f"median : \
{kmf.median_survival_time_}")
print(f"median confidence interval : \n \
{median_survival_times(kmf.confidence_interval_)}")
以下、実行結果です。
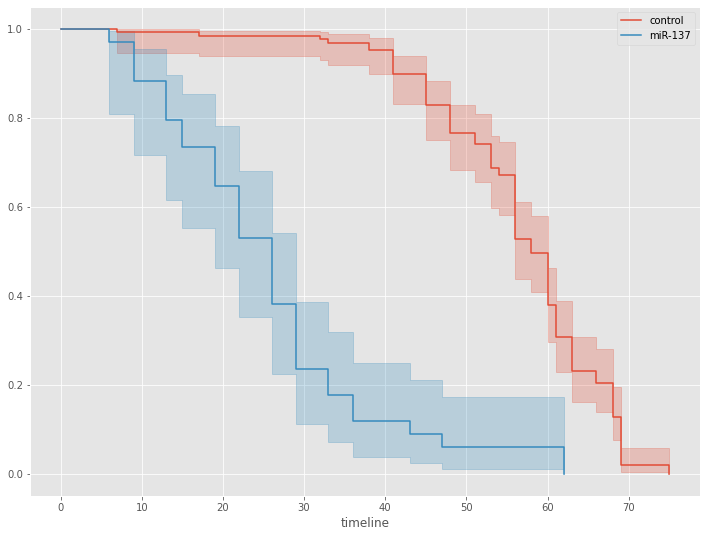
次に、群(miR-137群とコントロール群)別に生存関数を見てみます。
以下、コードです。
# 群別 生存関数 kmf_1 = KaplanMeierFitter() kmf_2 = KaplanMeierFitter() groups = df['group'] ix = (groups == 'miR-137') kmf_1.fit(T[~ix], E[~ix], label='control') ax = kmf_1.plot_survival_function() kmf_2.fit(T[ix], E[ix], label='miR-137') ax = kmf_2.plot_survival_function(ax=ax)
以下、実行結果です。
郡別の死亡時期の推定結果(中央値)です。
以下、コードです。
# 群別 推定結果(中央値と信頼区間)
print("[control]------------------------")
print(f"median : \
{kmf_1.median_survival_time_}")
print(f"median confidence interval : \n \
{median_survival_times(kmf_1.confidence_interval_)}")
print("\n")
print("[miR-137]------------------------")
print(f"median : \
{kmf_2.median_survival_time_}")
print(f"median confidence interval : \n \
{median_survival_times(kmf_2.confidence_interval_)}")
以下、実行結果です。
以上が、カプランマイヤー推定による、生存関数の推定と死亡時期の推定をするときのやり方です。
その2:回帰モデル用のダミーデータ
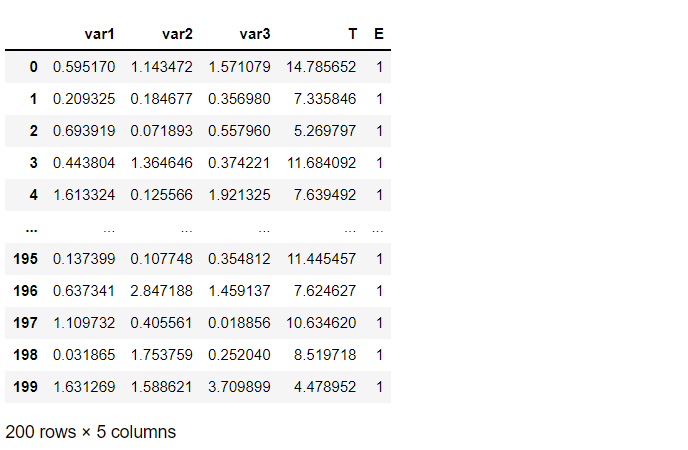
「生存日数」(T)と「イベント生起」(E)、そして幾つかの特徴量(説明変数X)からなるデータセットです。
先ず、カプランマイヤー推定法を使い先ほどと同様の分析をします。
データを読み込みます。以下、コードです。
# データセットの読み込み from lifelines.datasets import load_regression_dataset df = load_regression_dataset() df #確認
以下、実行結果です。
カプランマイヤー推定をします。以下、コードです。
# カプランマイヤー推定 T = df['T'] #生存期間 E = df['E'] #イベント生起 kmf = KaplanMeierFitter() kmf.fit(T, event_observed=E)
生存時間を表す確率変数Tの確率密度関数の累積確率分布を見てみます。この累積確率分布は、生存時間がt以上とならない確率です。
以下、コードです。
# 累積分布関数 kmf.plot_cumulative_density()
以下、実行結果です。
さらに、生存関数を見てみます。生存関数とは、生存時間がt以上となる確率、言い換えると、時刻tまでにイベント(例:離反)が発生していない確率です。
以下、コードです。
# 生存関数 kmf.plot_survival_function()
以下、実行結果です。
死亡時期を推定してみます。平均値ではなく中央値を使います。50%が死亡する時期です。
以下、コードです。
# 推定結果(中央値と信頼区間)
print(f"median : \
{kmf.median_survival_time_}")
print(f"median confidence interval : \n \
{median_survival_times(kmf.confidence_interval_)}")
以下、実行結果です。
次に、Cox比例ハザードモデル(Cox proportional hazard model)を使い、各特徴量(説明変数X)がどのように影響を及ぼすのかを分析していきます。
以下、コードです。
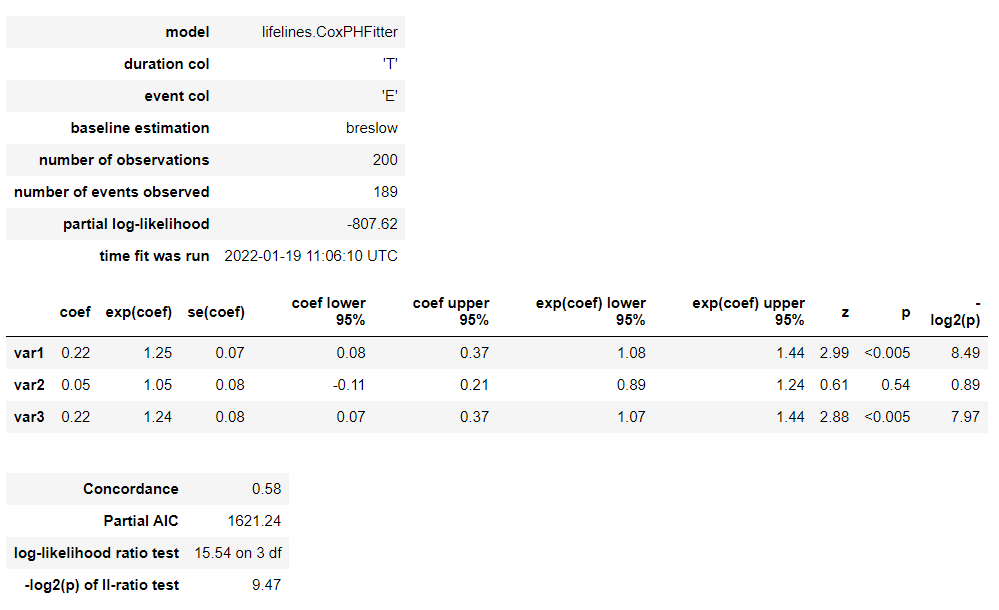
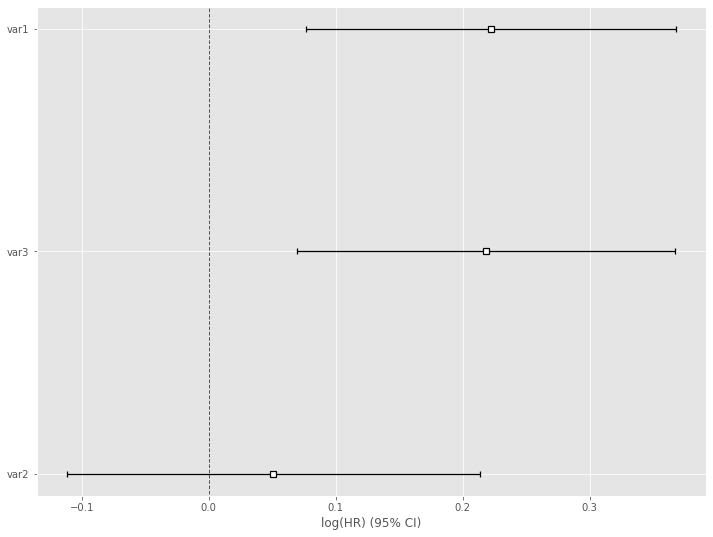
# Cox比例ハザード回帰 cph = CoxPHFitter() cph.fit(df, 'T', event_col='E') cph.print_summary() #サマリー cph.plot() #係数
以下、実行結果です。
各特徴量(説明変数X)が、どのような影響を及ぼすのかが見えてきます。この例では、特徴量 var1 が生存に悪影響を与えていることが分かります。
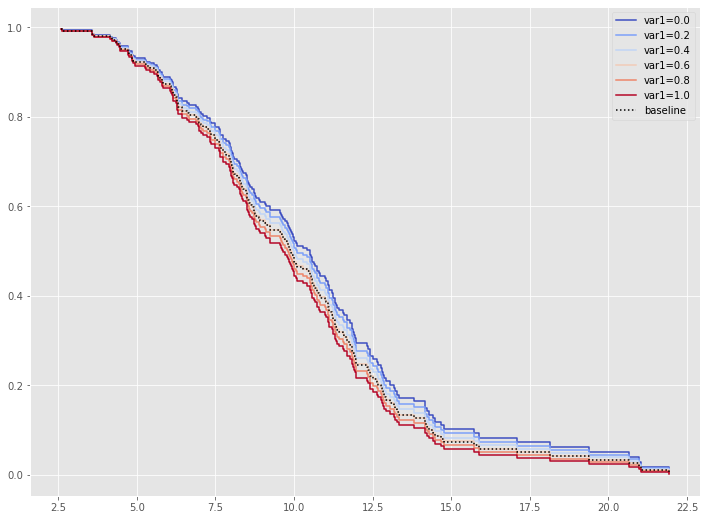
では、var1の値によって、生存関数がどのように変化するのかを視覚的に確認してみます。
以下、コードです。
# 特定の特徴量の影響の可視化
cph.plot_partial_effects_on_outcome(covariates='var1',
values=[0, 0.2, 0.4, 0.6, 0.8, 1],
cmap='coolwarm')
以下、実行結果です。
その3:出所後 1 年間追跡調査データ
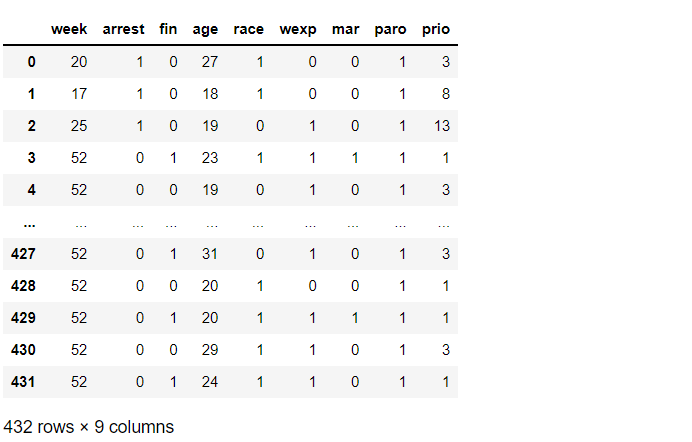
その2と同様に、「生存日数」(T)と「イベント生起」(E)、そして幾つかの特徴量(説明変数X)からなるデータセットです。
- week:出所後した後に逮捕されるまでの週数、または打ち切りまでの収集
- arrest:再逮捕されたかどうか(1:逮捕、0:打ち切り)
- fin:財政援助の有無 (1:Yes、0:No)
- age:出所時の年齢
- race:1:黒人、0:その他
- wexp:労働経験の有無 (1:Yes、0:No)
- mar:出所時の婚姻の有無 (1:Yes、0:No)
- paro:仮釈放の有無(1:Yes、0:No)
- prio:今までの受刑回数
ここでは、単なるCox比例ハザードモデル(Cox proportional hazard model)ではなく、Lasso(スパースモデリング)で実施していきます。
先ず、カプランマイヤー推定法を使い先ほどと同様の分析をします。
データを読み込みます。以下、コードです。
# データセットの読み込み from lifelines.datasets import load_rossi df = load_rossi() df #確認
以下、実行結果です。
カプランマイヤー推定をします。以下、コードです。
# カプランマイヤー推定 T = df['week'] #生存期間 E = df['arrest'] #イベント生起 kmf = KaplanMeierFitter() kmf.fit(T, event_observed=E)
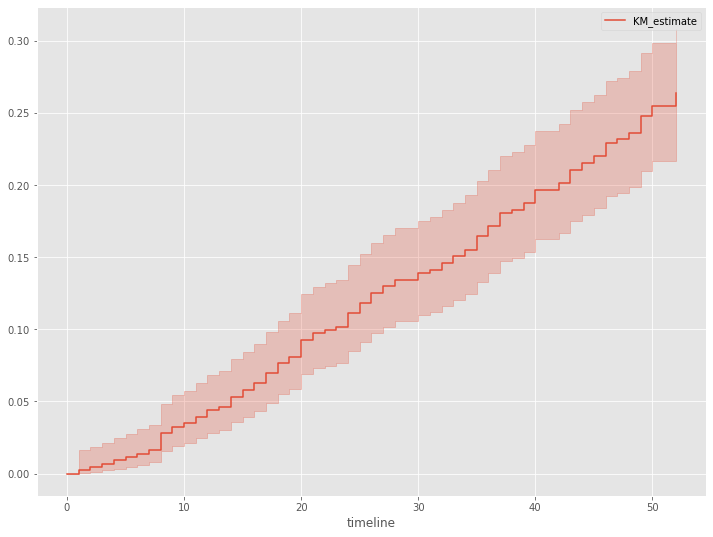
生存時間を表す確率変数Tの確率密度関数の累積確率分布を見てみます。この累積確率分布は、生存時間がt以上とならない確率です。
以下、コードです。
# 累積分布関数 kmf.plot_cumulative_density()
以下、実行結果です。
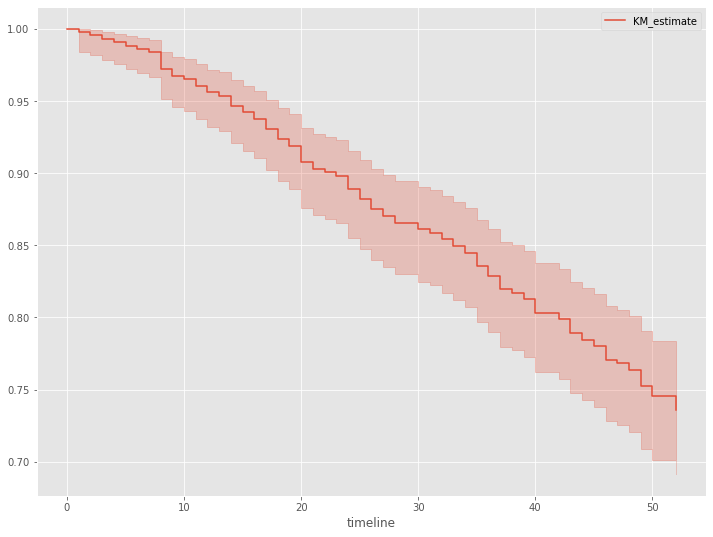
さらに、生存関数を見てみます。生存関数とは、生存時間がt以上となる確率、言い換えると、時刻tまでにイベント(例:離反)が発生していない確率です。
以下、コードです。
# 生存関数 kmf.plot_survival_function()
以下、実行結果です。
Lasso(スパースモデリング)なCox比例ハザードモデル(Cox proportional hazard model)の前に、比較のため通常のCox比例ハザードモデル(Cox proportional hazard model)を使い、各特徴量(説明変数X)がどのように影響を及ぼすのかを分析していきます。
以下、コードです。
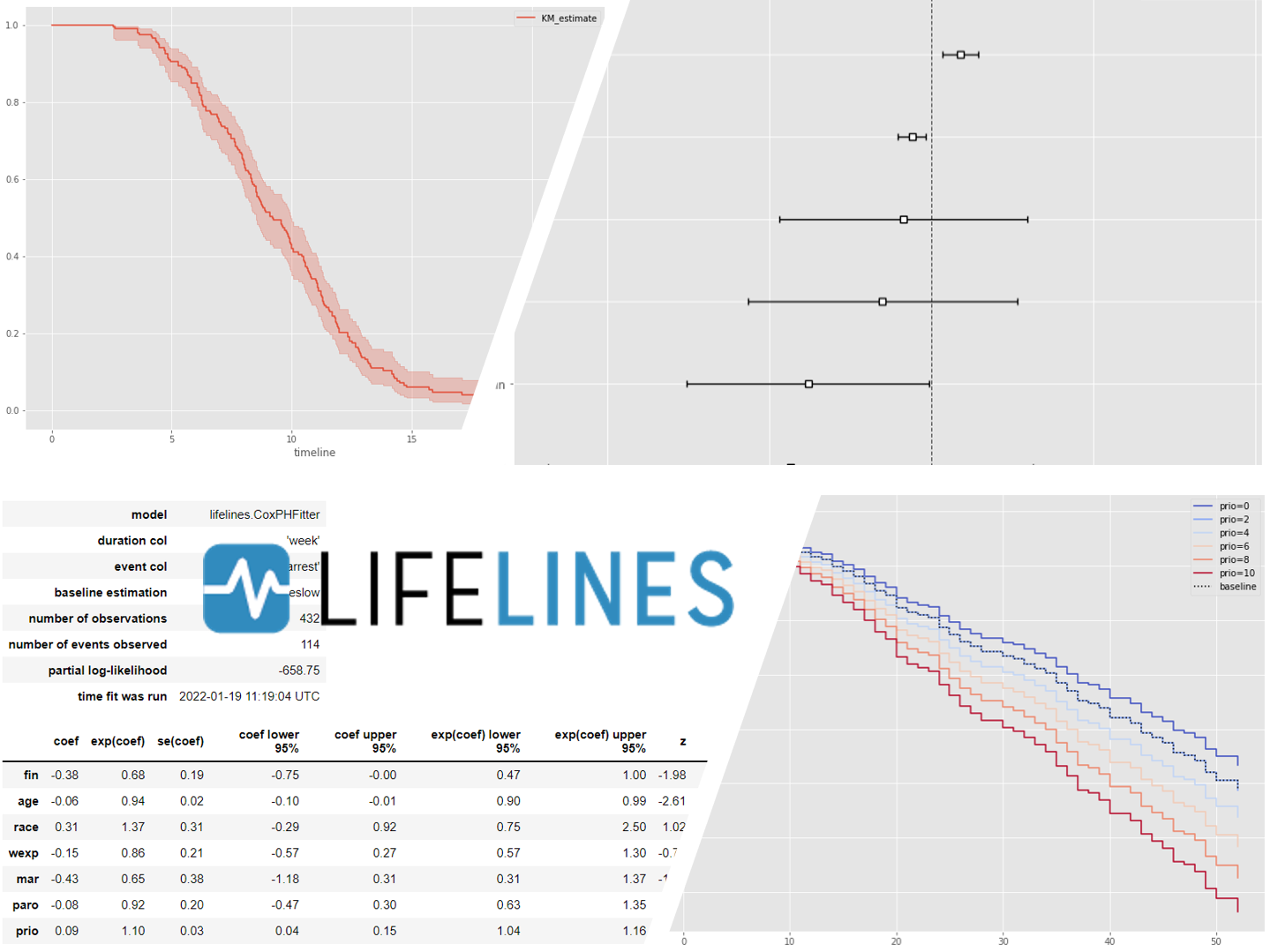
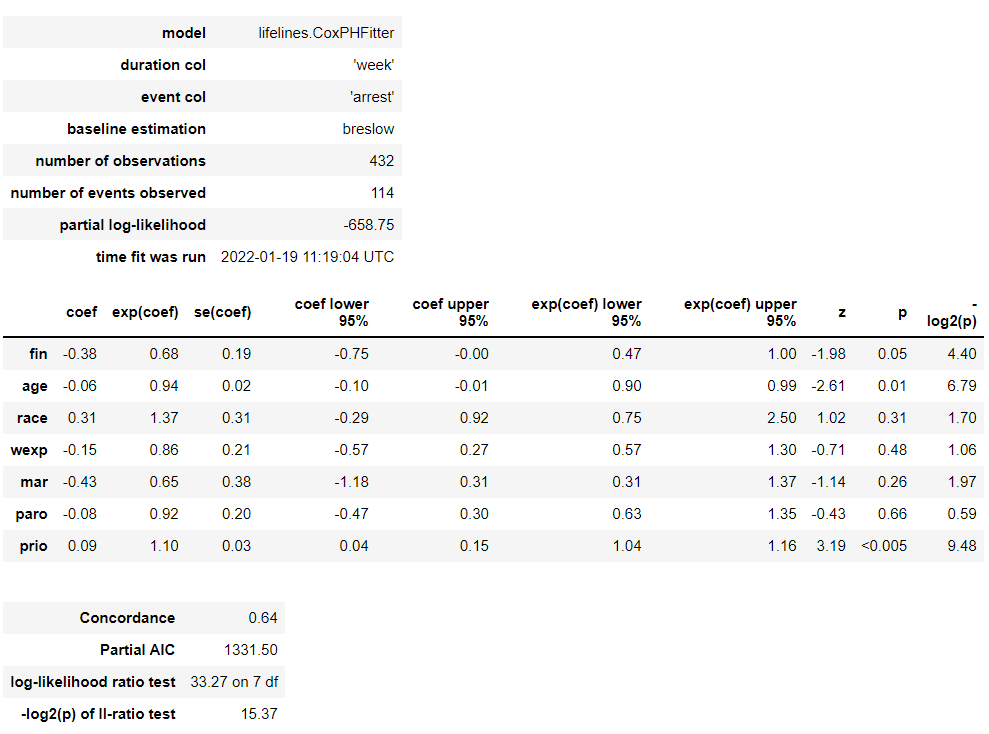
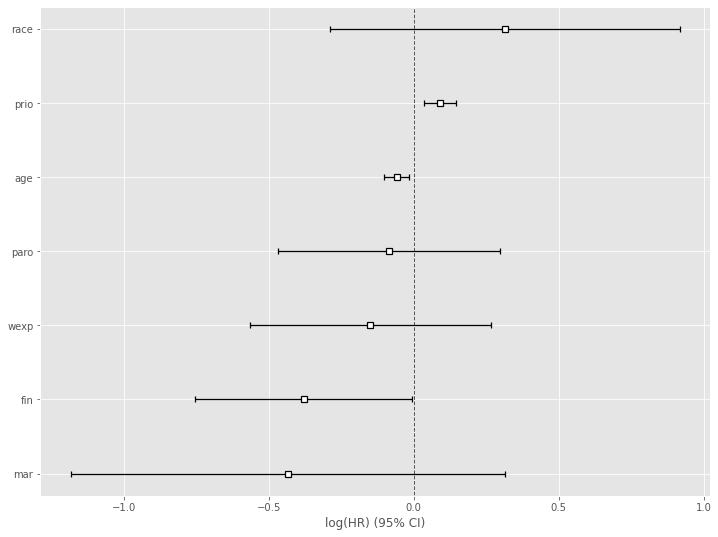
# Cox比例ハザード回帰 cph = CoxPHFitter() cph.fit(df, duration_col='week', event_col='arrest') cph.print_summary() #サマリー cph.plot() #係数
以下、実行結果です。
次に、Lasso(スパースモデリング)なCox比例ハザードモデル(Cox proportional hazard model)を使い、各特徴量(説明変数X)がどのように影響を及ぼすのかを分析していきます。
以下、コードです。
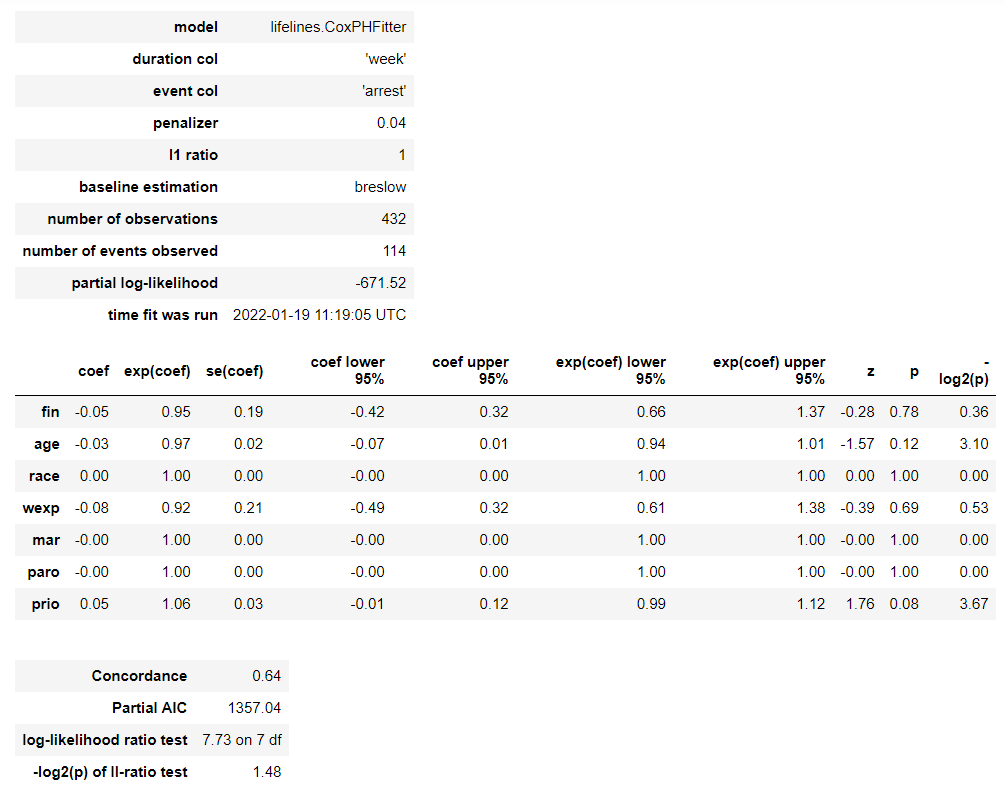
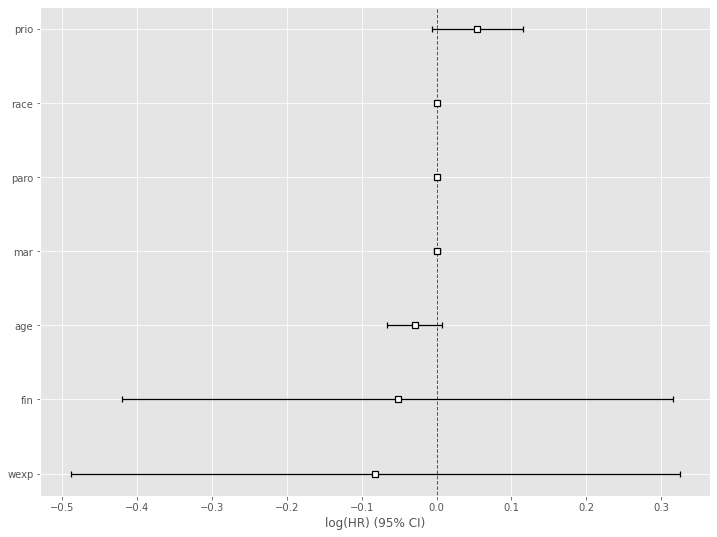
# Cox比例ハザード回帰(Lasso) cph = CoxPHFitter(penalizer=0.04, l1_ratio=1) cph.fit(df, duration_col='week', event_col='arrest') cph.print_summary() #サマリー cph.plot() #係数
以下、実行結果です。
各特徴量(説明変数X)が、どのような影響を及ぼすのかが見えてきます。
この例では、特徴量 prio(今までの受刑回数)が生存(再逮捕されない)に悪い影響を与えていることが分かります。一方、特徴量 wexp(労働経験の有無 (1:Yes、0:No))が生存(再逮捕されない)に良い影響を与えていることが分かります。
解釈例として、受刑回数が多いほど再販し、労働経験があるほど再犯しない、という見方もできます。
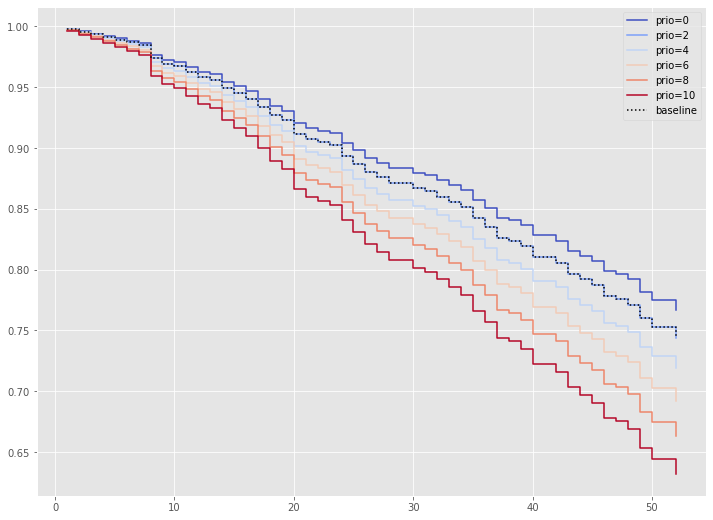
では、prio(今までの受刑回数)の値によって、生存関数がどのように変化するのかを視覚的に確認してみます。
以下、コードです。
# 特定の特徴量の影響の可視化(prio)
cph.plot_partial_effects_on_outcome(covariates='prio',
values=[0, 2, 4, 6, 8, 10],
cmap='coolwarm')
以下、実行結果です。
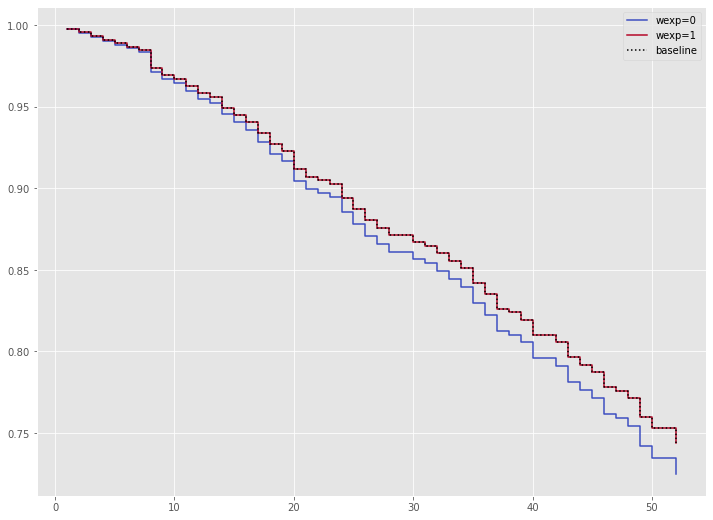
wexp(労働経験の有無 (1:Yes、0:No))の値によって、生存関数がどのように変化するのかを視覚的に確認してみます。
以下、コードです。
# 特定の特徴量の影響の可視化(wexp)
cph.plot_partial_effects_on_outcome(covariates='wexp',
values=[0, 1],
cmap='coolwarm')
以下、実行結果です。
次回
次回は、通信会社の顧客離反の事例データを使い、離反時期の予測の仕方を説明します。
【生存時間分析による離反時期分析 その2】Python の生存時間分析ライブラリー Lifelines で実施する 「離反時期(顧客であるまでの期間)分析」