【生存時間分析による離反時期分析 その2】
Python の生存時間分析ライブラリー Lifelines で実施する
「離反時期（顧客であるまでの期間）分析」

6905
【生存時間分析による離反時期分析 その2】Python の生存時間分析ライブラリー Lifelines で実施する 「離反時期（顧客であるまでの期間）分析」

離反時期や故障時期などを分析する生存時間分析を実施する手段は色々ありますが、生存時間用のライブラリーを活用するのがいいでしょう。

今回利用するのは、LifelinesというPythonのライブラリーです。

生存時間分析ライブラリー Lifelinesのインストールや使い方については、簡単に以下の記事で説明しています。

【生存時間分析による離反時期分析 その1】
離反時期の予測に使えるPython の
生存時間分析ライブラリー Lifelines に慣れよう！

今回は、通信会社の顧客離反の事例データを使い、離反時期の予測の仕方を説明します。

生存時間分析ライブラリー Lifelines がインストールしていることを前提に、お話しを進めます。

サンプルデータ

通信会社の顧客の離反データ（Kaggleのサンプルデータ）を使います。以下のKaggleのページからCSVファイルをダウンロードしてお使いください。

Telco Customer Churn

生存時間として「契約期間」（tenure）、イベント生起として「離反」（Churn）となります。変数 customerID は個人を識別するIDで、その他の変数は、特徴量（説明変数X）です。

  • tenure：契約期間（生存時間）
  • Churn：離反（イベント生起）

 

全体の流れ

通信会社の顧客の離反データを使った、離反時期（顧客であるまでの期間）分析の流れです。

  1. ライブラリー読み込み
  2. データセット読み込み
  3. データの前処理その1（カプランマイヤー推定用）
  4. カプランマイヤー推定の実施（全体の生存時間の分析）
  5. データの前処理その2（Cox比例ハザード回帰用）
  6. Cox比例ハザード回帰の実施（個々の生存時間の分析）
  7. 継続顧客（離反していない顧客）の離反時期予測

では、分析を進めていきます。

 

1. ライブラリー読み込み

必要なライブラリーを読み込みます。

以下、コードです。

# 必要なライブラリーの読み込み
import pandas as pd 
import numpy as np
from lifelines import *
from lifelines.utils import median_survival_times
import matplotlib.pyplot as plt 

# グラフのスタイル
plt.style.use('ggplot')

# グラフサイズ設定
plt.rcParams['figure.figsize'] = [12, 9]

 

生存時間分析ライブラリー Lifelines 以外は、よく使う一般的なPythonのライブラリーです。

 

2. データセット読み込み

通信会社の顧客の離反データ（Kaggleのサンプルデータ）を読み込みます。

以下、コードです。

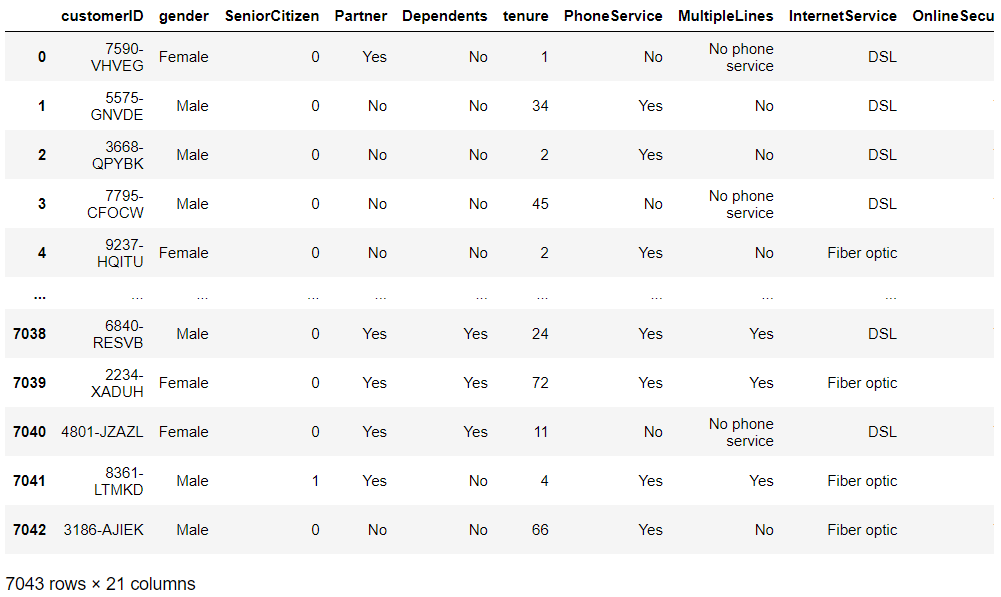
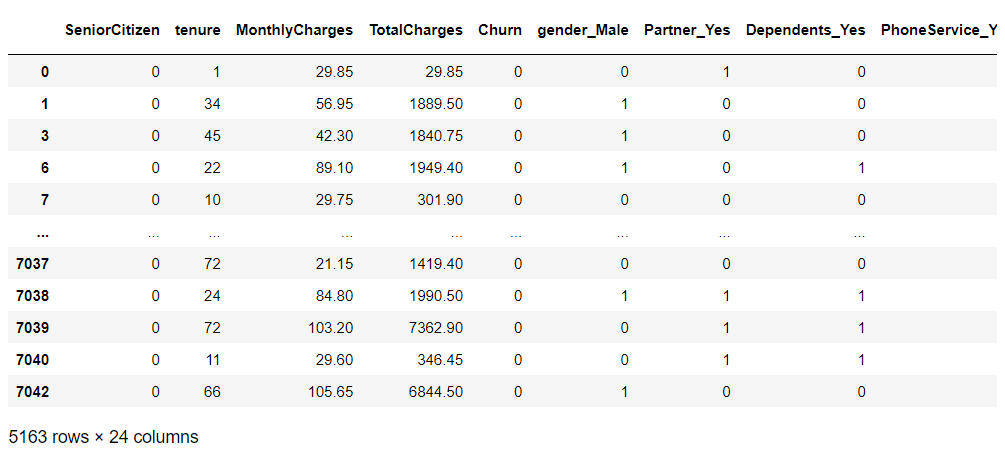
# データセットの読み込み
data_path = 'C:\dataset\WA_Fn-UseC_-Telco-Customer-Churn.csv'
df = pd.read_csv(data_path)
df #確認

 

以下、実行結果です。

 

PCのCドライブにあるフォルダ「dataset」に、「WA_Fn-UseC_-Telco-Customer-Churn.csv」というファイル名で格納した場合の例です。

 

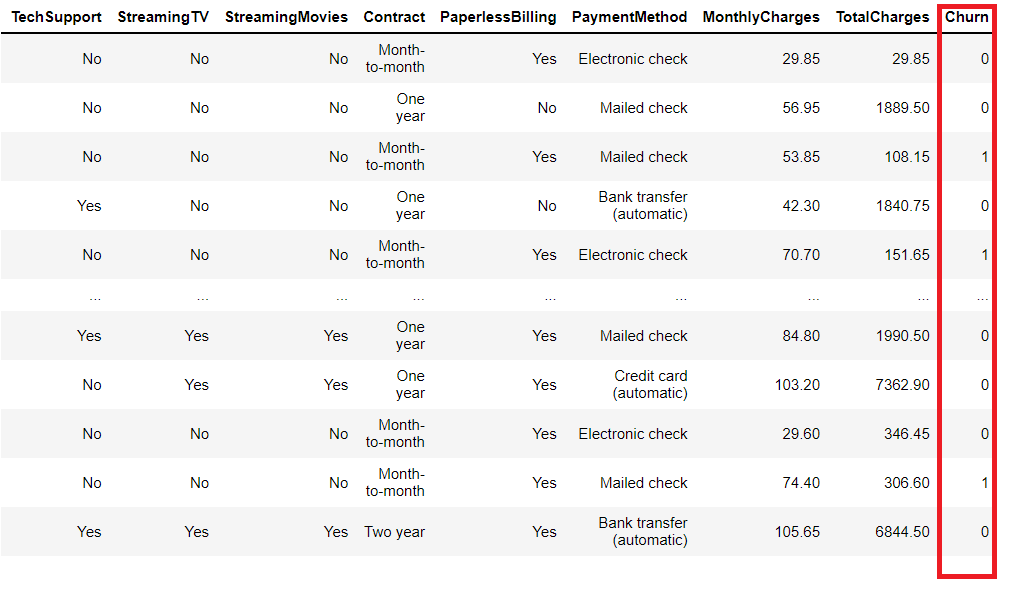
出力したデータセットの一部を見てもらうと分かりますが、変数「Churn」が「Yes」や「No」というテキストが入力されています。

変数「Churn」を以下のように変換する必要があります。

  • Yes → 1
  • No → 0

前処理時に、そのあたりの処理を実施します。

 

3. データの前処理その1（カプランマイヤー推定用）

カプランマイヤー推定を行う前に、簡単な前処理を実施する必要があります。

先ず、データセットの状況を簡単に確認します。

以下、コードです。

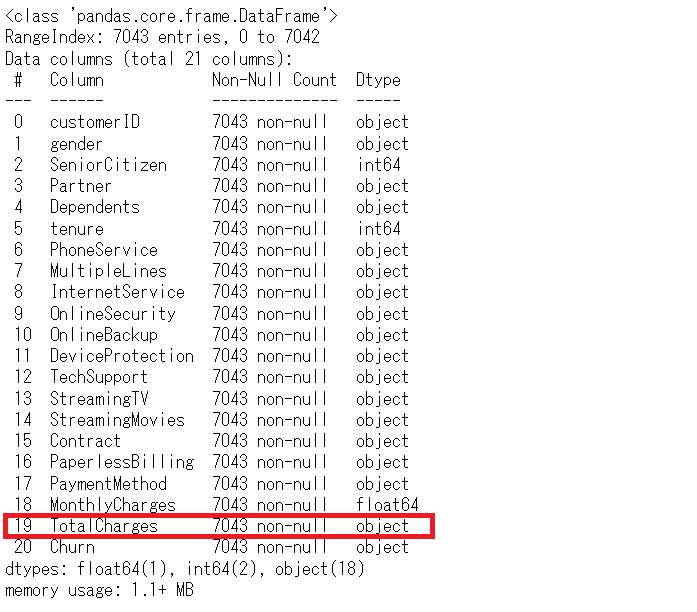
# データセットの状況の確認
df.info()

 

以下、実行結果です。

 

データセットを読み込んだときに、確認のために出力したデータセットの一部と見比べてもらうと分かりますが、数値であるべき変数「TotalCharges」がカテゴリカル変数になっています。欠測している箇所が空白になっていることが影響してそうです。

ここで、次の2つの前処理を順番に実施していきます。

  • TotalCharges に対する前処理
  • Churn に対する前処理

 

先ずは、TotalChargesに対する前処理です。

数値型へ強引に型変換します。以下、コードです。

# TotalCharges変数を型変換（数値型へ）
df.TotalCharges = pd.to_numeric(df.TotalCharges,
                                errors='coerce')

 

確認してみます。以下、コードです。

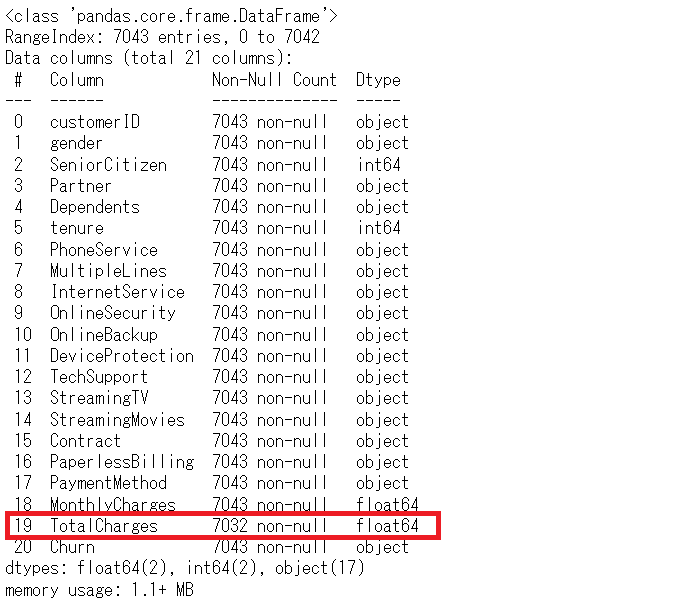
# データセットの状況の確認
df.info()

 

以下、実行結果です。

 

型変換（float64になっている）が上手く行ったことが分かります。

今回の型変換は、強引に行ったので欠測値が生まれた可能性があるため、確認してみます。

以下、コードです。

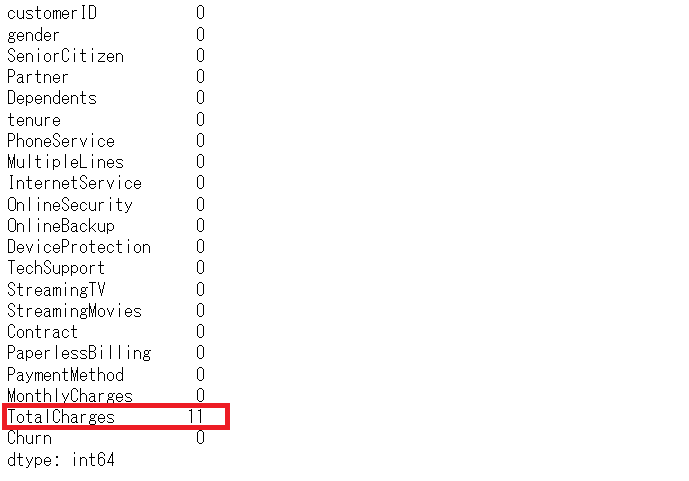
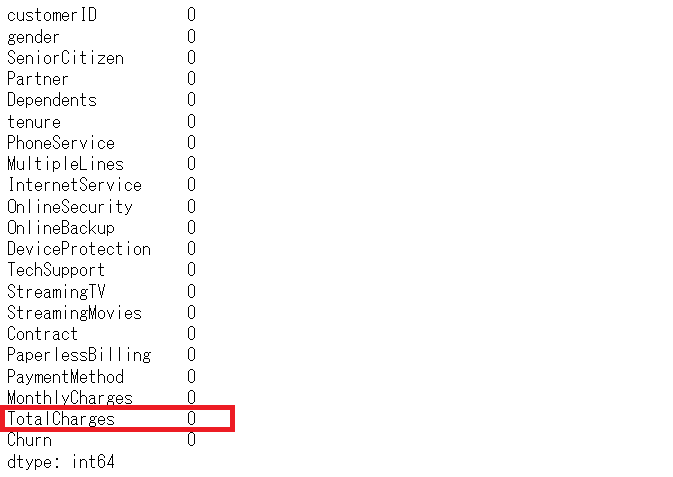
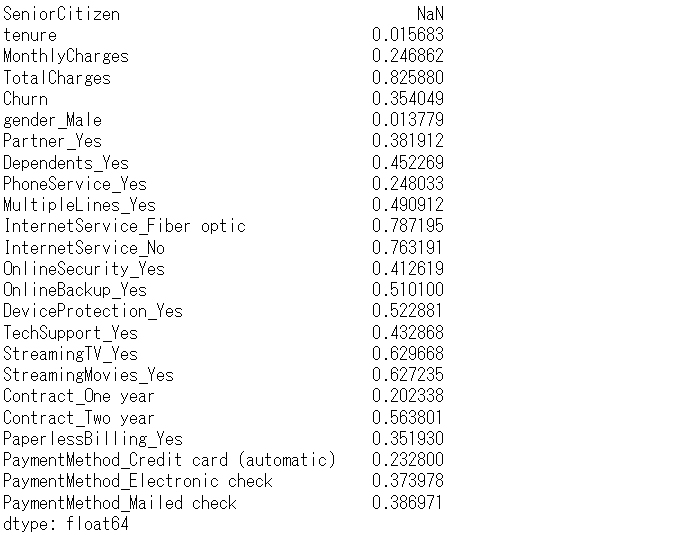
# 欠測状況の確認
df.isnull().sum()

 

以下、実行結果です。

 

欠測した箇所が、TotalChargesに11箇所あります。今回は、欠測値のある行を分析対象から削除します。

以下、コードです。

# 欠測値のある行を削除する
df = df.dropna(how='any')

 

確認してみます。以下、コードです。

# 欠測状況の確認
df.isnull().sum()

 

以下、実行結果です。

 

次は、Churnに対する前処理です。

変数「Churn」を以下のように変換します。

  • Yes → 1
  • No → 0

以下、コードです。

# Churnの値変換（Yes:1、No:0）
df = df.replace({'Churn':{'Yes':1, 'No':0}})
df #確認

 

以下、実行結果です。

 

変換されていることが分かります。

このデータセットを使い、カプランマイヤー推定を実施していきます。

 

4. カプランマイヤー推定の実施（全体の生存時間の分析）

カプランマイヤー推定をします。以下、コードです。

# カプランマイヤー推定
T = df['tenure'] #生存期間（契約期間）
E = df['Churn'] #イベント生起（離反）
kmf = KaplanMeierFitter()
kmf.fit(T, event_observed=E)

 

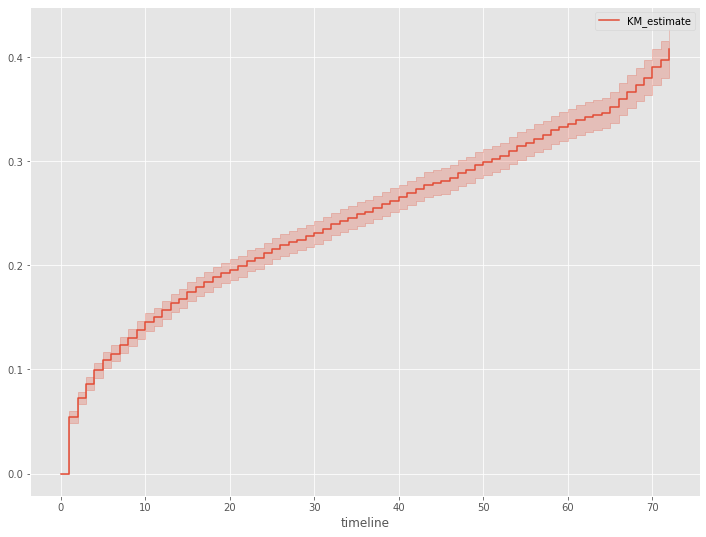
生存時間を表す確率変数Tの確率密度関数の累積確率分布を見てみます。この累積確率分布は、生存時間がt以上とならない確率です。

以下、コードです。

# 累積分布関数
kmf.plot_cumulative_density()

 

以下、実行結果です。

 

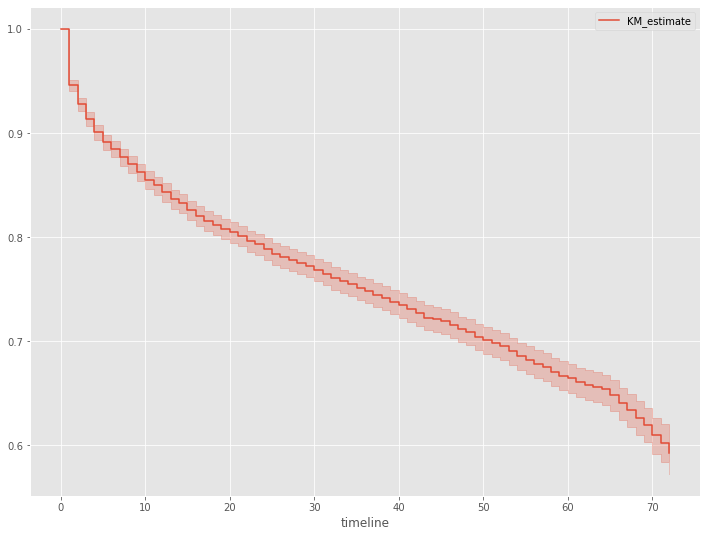
さらに、生存関数を見てみます。生存関数とは、生存時間がt以上となる確率、言い換えると、時刻tまでにイベント（例：離反）が発生していない確率です。

以下、コードです。

# 生存関数
kmf.plot_survival_function()

 

以下、実行結果です。

 

生存率は、契約直後と契約から65日後あたりで急激に落ちていることが分かります。

 

5. データの前処理その2（Cox比例ハザード回帰用）

Cox比例ハザード回帰のための前処理を実施していきます。

目的変数など最低限必要な変数に関しては、先程前処理を終えているので、ここで実施する前処置は特徴量（説明変数X）に対するものです。

先ずは、カテゴリカル変数をダミーコード（0-1変数）化します。

以下、コードです。

# カテゴリカル変数のダーミ変数化（One Hot Encode）
df_dummy = pd.get_dummies(df.drop('customerID', axis=1),
                          drop_first=True)

 

どうなったのか、簡単に確認してみます。

以下、コードです。

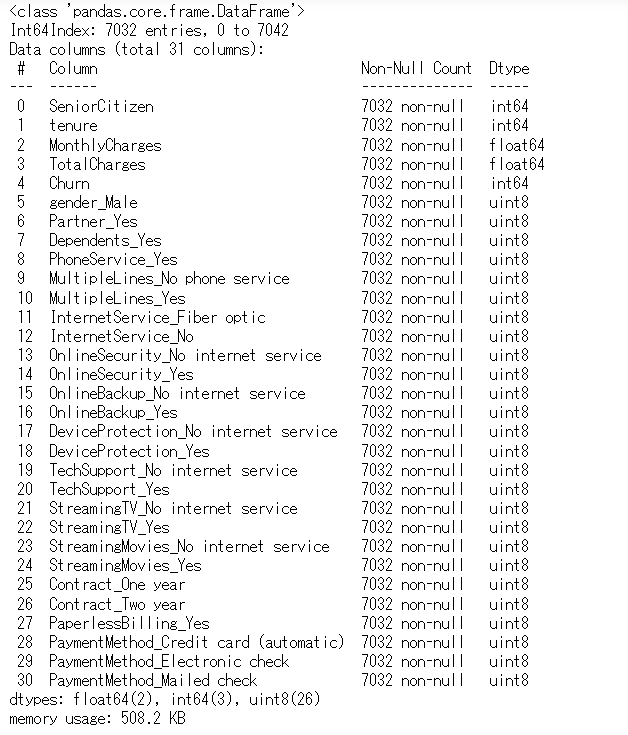
# データセット状況の確認
df_dummy.info()

 

以下、実行結果です。

 

変数が増え、ダミーコード化されていることが分かります。

 

次に、特徴量（説明変数X）同士の相関が異常に高い（-1 or 1）特徴量（説明変数X）の組み合わせを探し、どちらか一方を特徴量（説明変数X）から除外します。

特徴量（説明変数X）同士の相関の絶対値を見てみます。

以下、コードです。

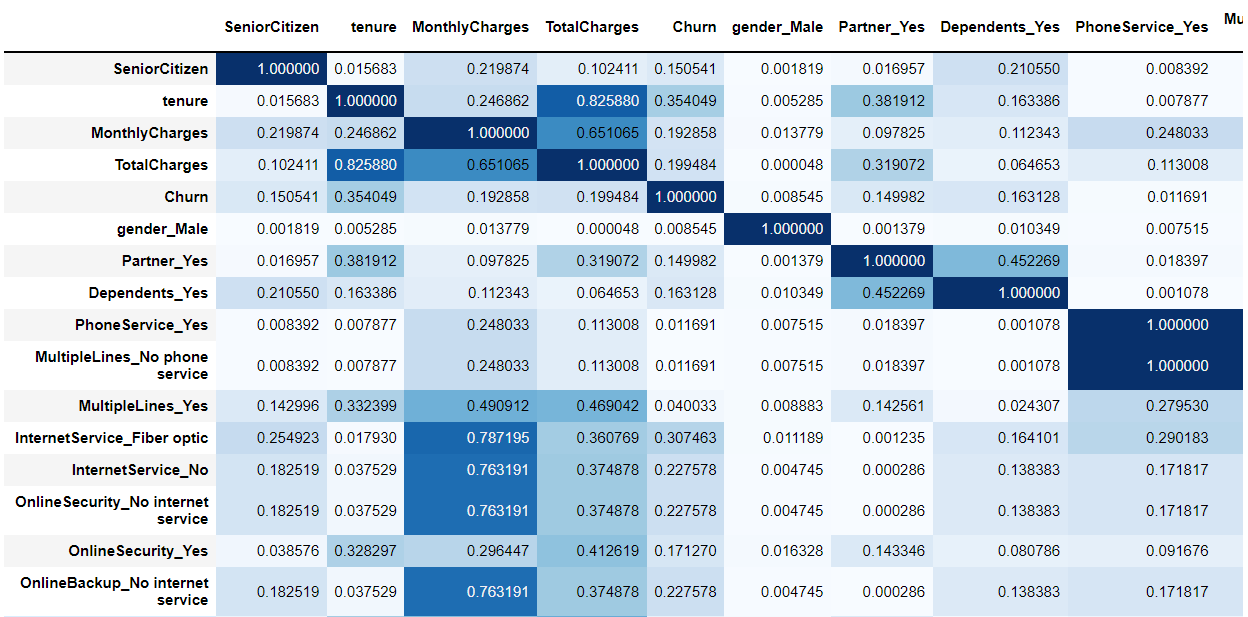
# 相関係数行列（絶対値）
abs(df_dummy.corr()).style.background_gradient(cmap='Blues')

 

以下、実行結果です。

 

対角線は自分自身同士の相関係数の絶対値なので「1」の値が入っています。問題になるのは、対角線でないのに「1」の値が入っているケースです。

対角線でないのに「1」の値が入っているケースが、パッと見ただけで発見されます。

では、対角線でないのに「1」の値が入っている特徴量（説明変数X）同士の相関が異常に高い組み合わせを抽出していきます。

流れです。

  1. 相関の絶対値の行列の上三角行列を作る
  2. 上三角行列を縦持ちのデータセットへ変換する
  3. 相関の絶対値の高い特徴量（説明変数X）の組み合わせを抽出する

では、相関の絶対値の行列の上三角行列を作ります。

以下、コードです。

# 上三角行列
arr = np.triu(abs(df_dummy.corr()), 1)
res = pd.DataFrame(np.where(arr, arr, np.nan),
                   index=df_dummy.corr().index,
                   columns=df_dummy.corr().columns)
res #確認

 

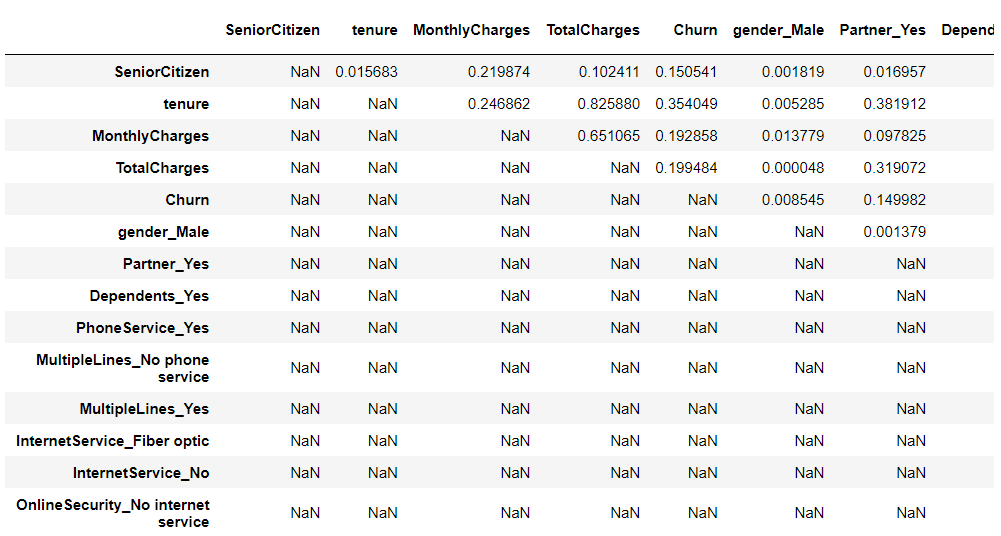
以下、実行結果です。

 

上三角行列を縦持ちのデータセットへ変換します。

以下、コードです。

# 縦持ちのデータに変換（相関係数の絶対値の高い順）
res.melt(ignore_index=False).dropna(how='any').sort_values('value',ascending=False)

 

以下、実行結果です。

 

相関の絶対値の高い特徴量（説明変数X）の組み合わせを抽出します。

以下、コードです。

# 高相関（相関係数の絶対値がほぼ1の変数の組み合わせ）を抽出
df_corr_melt = res.melt(ignore_index=False).dropna(how='any')
df_corr_melt[df_corr_melt.value >= 0.99999]

 

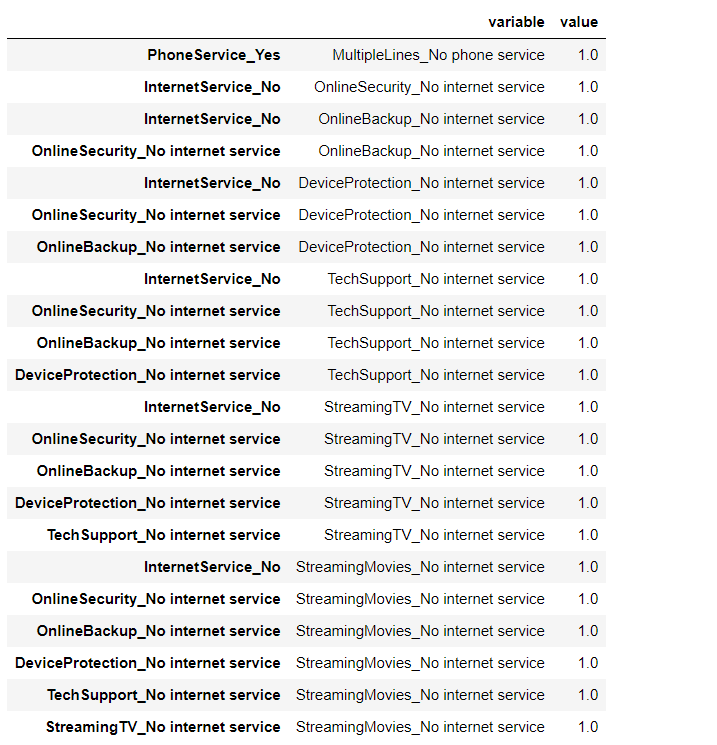
以下、実行結果です。

 

この表のvariable列に表示されている変数を削除します。

以下、コードです。

# 変数削除
del_col = df_corr_melt[df_corr_melt.value >= 0.99999].variable.unique()
df_dummy = df_dummy.drop(del_col, axis=1)

 

削除済みのデータセットから、相関の絶対値の行例の上三行列を作成し、各特徴量（説明変数X）と他の各特徴量（説明変数X）との相関の絶対値の最大値を計算してみます。

以下、コードです。

# 上三角行列
arr = np.triu(abs(df_dummy.corr()), 1)
res = pd.DataFrame(np.where(arr, arr, np.nan),
                   index=df_dummy.corr().index,
                   columns=df_dummy.corr().columns)

# 最大値
res.max()

 

以下、実行結果です。

 

各特徴量（説明変数X）と他の各特徴量（説明変数X）との相関の絶対値の最大値は、すべて1未満のため、上手く削除できていることが分かります。

このデータセットを使い、Cox比例ハザード回帰モデルを構築していきます。

 

6. Cox比例ハザード回帰の実施（個々の生存時間の分析）

Lasso（スパースモデリング）なCox比例ハザードモデル（Cox proportional hazard model）の前に、比較のため通常のCox比例ハザードモデル（Cox proportional hazard model）を使い、各特徴量（説明変数X）がどのように影響を及ぼすのかを分析していきます。

以下、コードです。

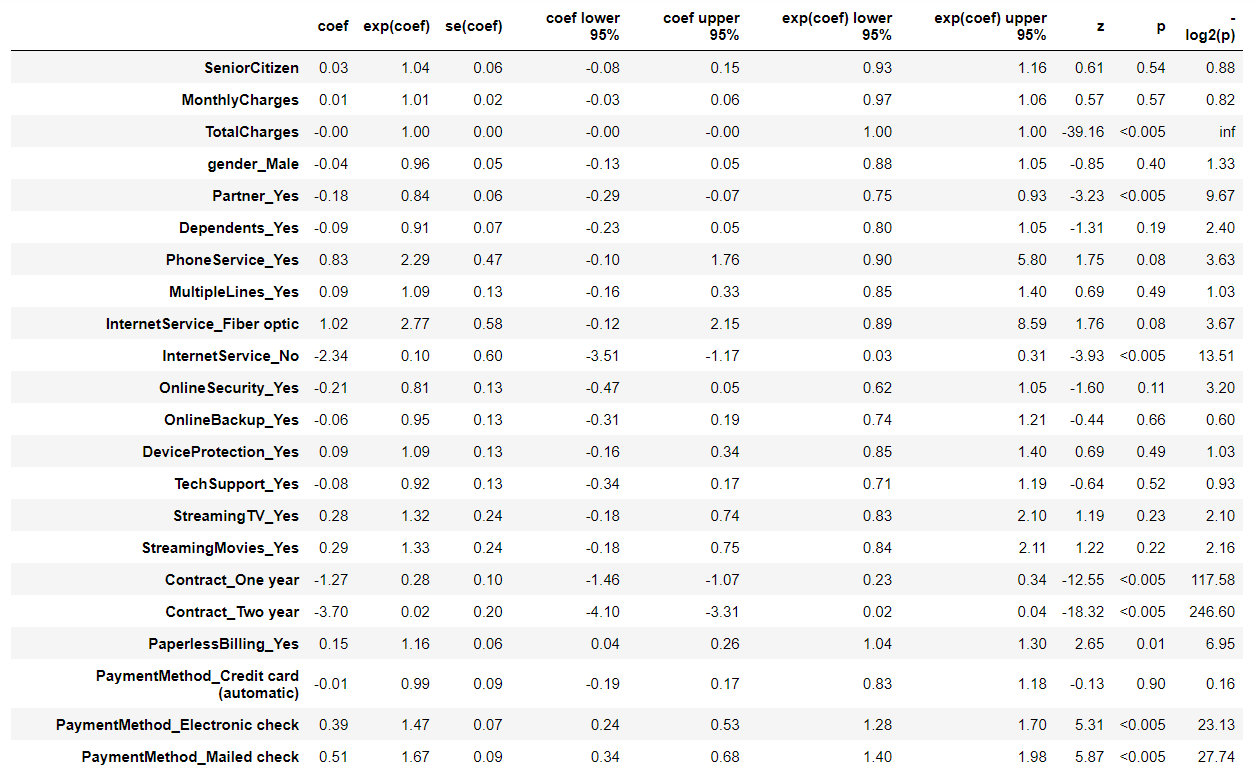
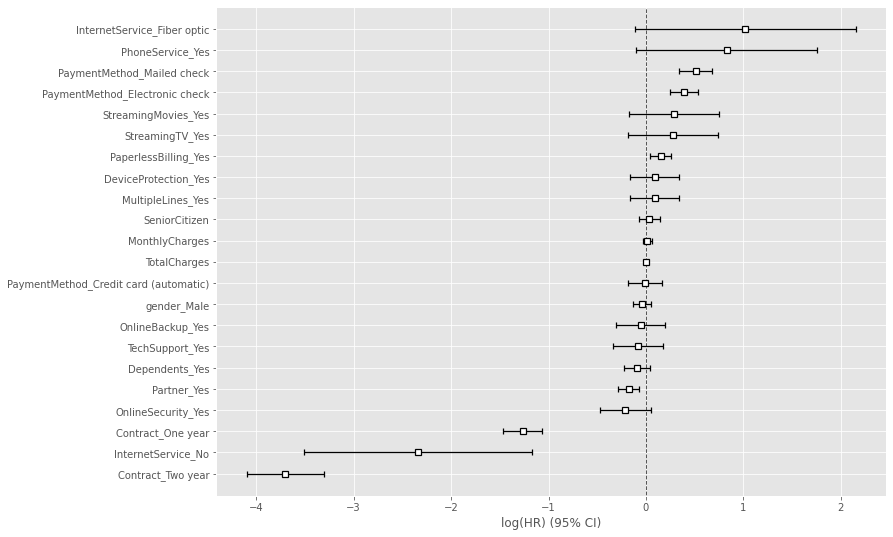
# Cox比例ハザード回帰
cph = CoxPHFitter()
cph.fit(df_dummy, duration_col='tenure', event_col='Churn') 

cph.print_summary() #サマリー
cph.plot() #係数

 

以下、実行結果です。

 

次に、Lasso（スパースモデリング）なCox比例ハザードモデル（Cox proportional hazard model）を使い、各特徴量（説明変数X）がどのように影響を及ぼすのかを分析していきます。

以下、コードです。

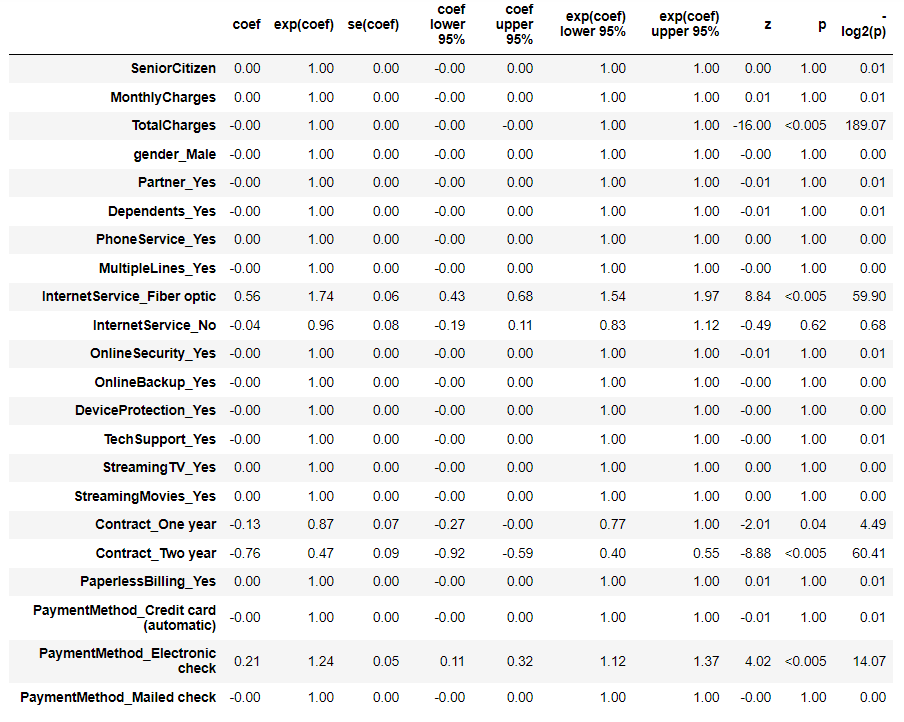
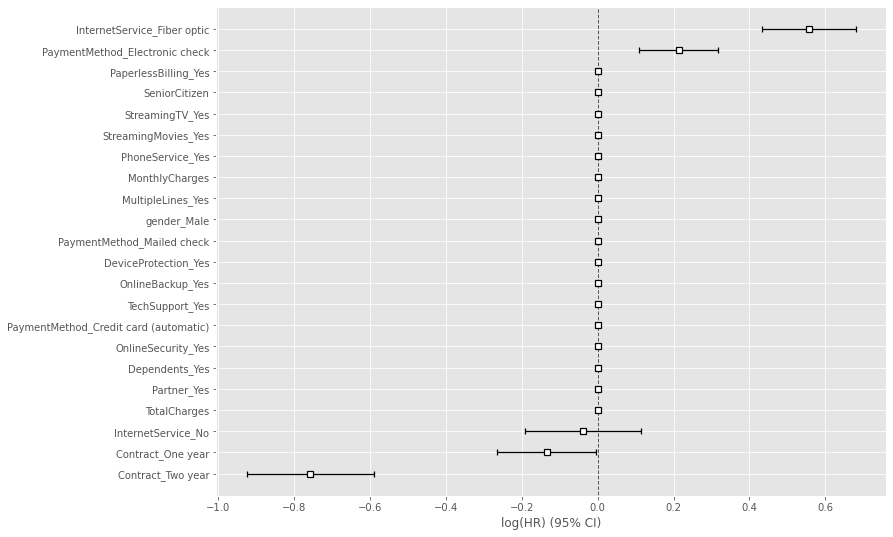
# Cox比例ハザード回帰（Lasso）
cph = CoxPHFitter(penalizer=0.1, l1_ratio=1)
cph.fit(df_dummy, duration_col='tenure', event_col='Churn') 

cph.print_summary() #サマリー
cph.plot() #係数

 

以下、実行結果です。

 

このモデルを使って、離反していない継続顧客が、今後どの時期に離反しそうかを予測し分析していきます。

 

7. 継続顧客（離反していない顧客）の離反時期予測

離反していない継続顧客を抽出します。

以下、コードです。

# 継続顧客（離反していない顧客）データの抽出
customers_data = df_dummy[df_dummy['Churn'] == 0]
customers_data #確認

 

以下、実行結果です。

 

継続顧客（離反していない顧客）の生存関数です。

以下、コードです。

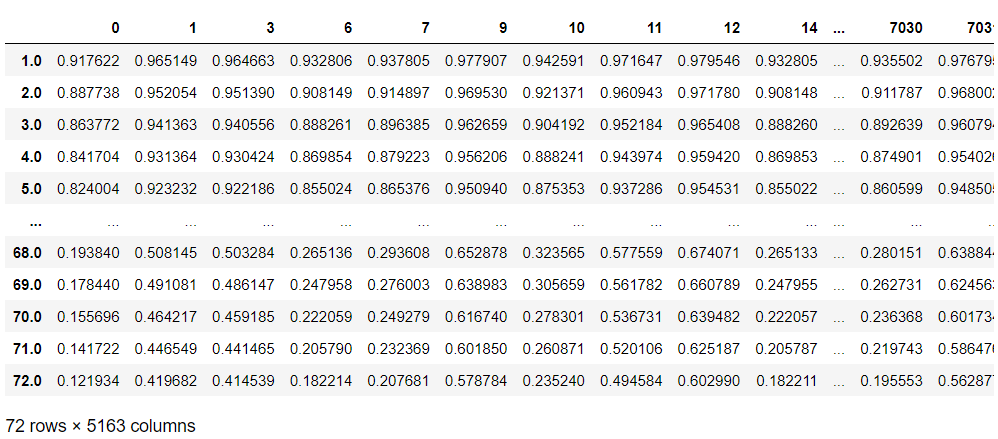
# 継続顧客の生存関数
pred_survival = cph.predict_survival_function(customers_data)
pred_survival #確認

 

以下、実行結果です。

 

この生存関数は、誕生から（契約してから）を想定しています。打ち切られた時期までは、契約後解約していないので、生存率100%です。

そのため、打ち切られた時期までは生存したという条件とした生存関数を再計算する必要があります。要するに、条件付き生存確率を求める必要があります。

以下、コードです。

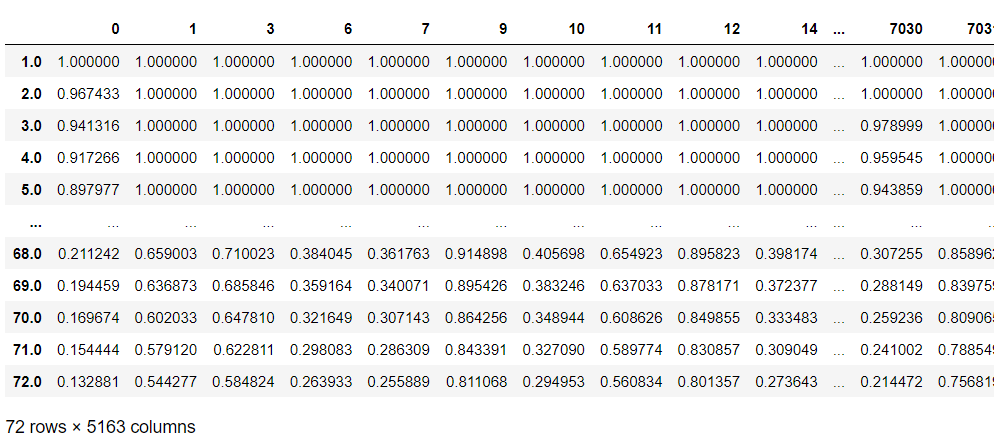
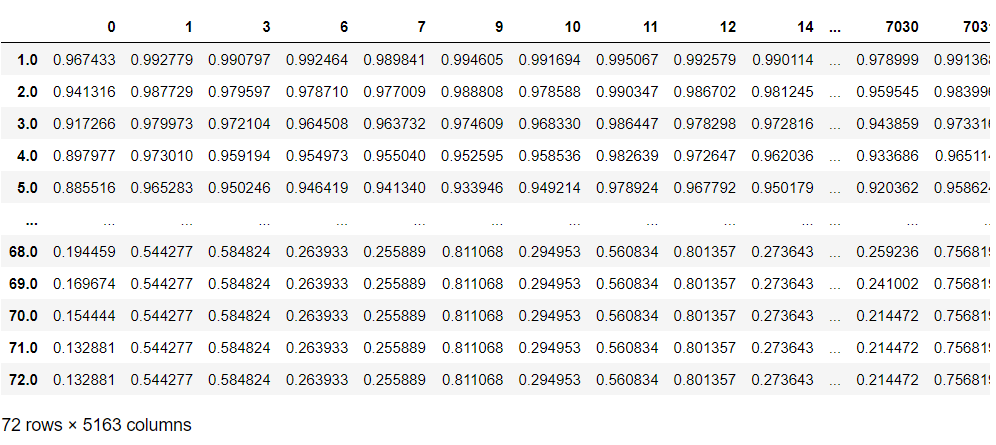
# 継続顧客の生存関数の修正（条件付き生存関数）
pred_survival_new = pred_survival.apply(lambda c: (c / c.loc[df_dummy.loc[c.name, 'tenure']])).clip(upper=1)
pred_survival_new #確認

 

以下、実行結果です。

 

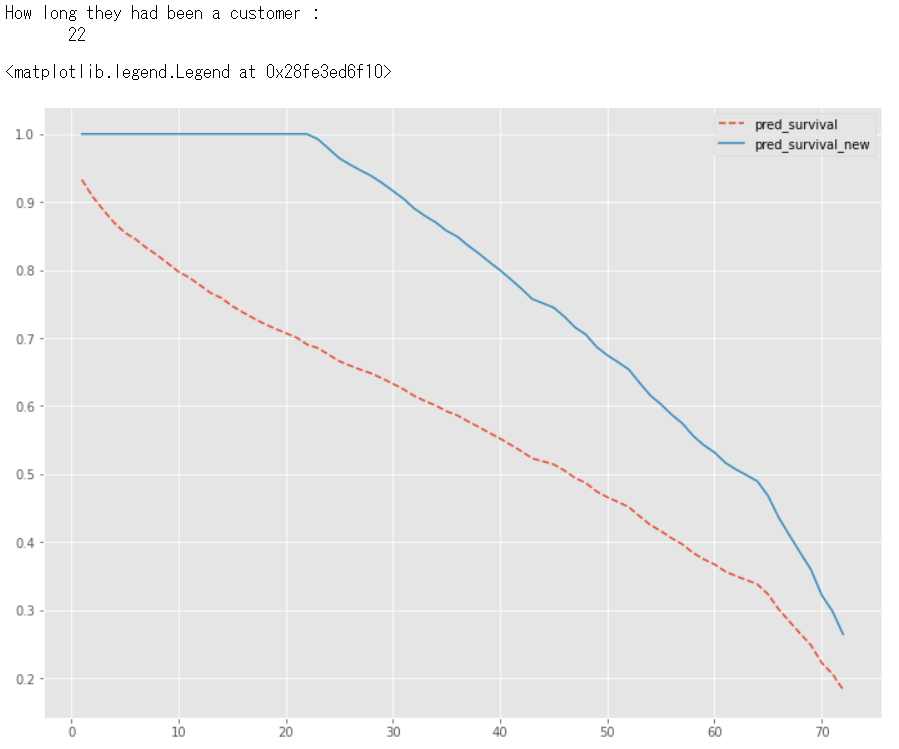
グラフで、特定の顧客に対し、修正前の生存関数（pred_survival）と、修正後の条件付き生存関数（pred_survival_new）を比較してみます。

以下、コードです。

# 特定の継続顧客の生存関数のグラフ化
customer = 6
print(f"How long they had been a customer : \n \
      {df_dummy.loc[customer, 'tenure']}")
pred_survival[customer].plot(ls="--", label="pred_survival")
pred_survival_new[customer].plot(label="pred_survival_new")
plt.legend()

 

以下、実行結果です。

 

この顧客（customer = 6）のデータが打ち切られた時期は、契約後「22」日です。少なくとも、22日までの生存率は100%です。

修正前の生存関数（pred_survival）と、修正後の条件付き生存関数（pred_survival_new）を比較するために、やや面倒な方法で修正後の条件付き生存関数（pred_survival_new）を構築しました。

打ち切り後の生存関数（条件付き生存関数）だけであれば、もっと簡単に作れます。

以下、コードです。

# 打ち切り後の未来
## 継続顧客の生存関数（生存した期間を条件とした生存関数）
pred_survival_new_remain = cph.predict_survival_function(
    customers_data,
    conditional_after=customers_data['tenure']
)
pred_survival_new_remain #確認

 

以下、実行結果です。

 

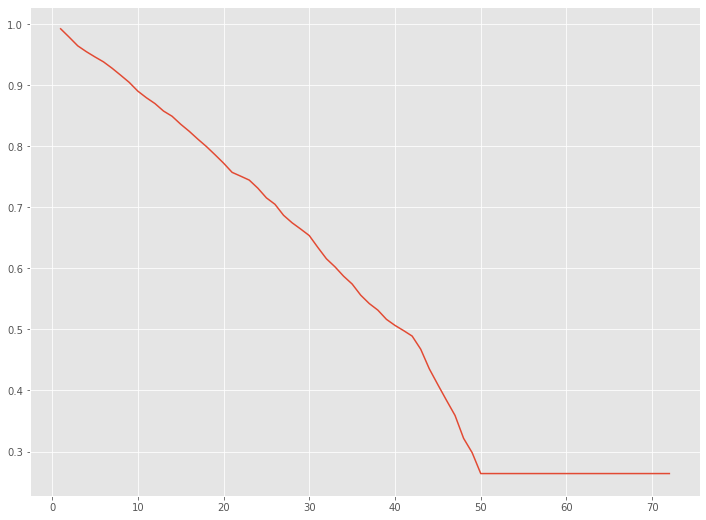
特定の顧客の、修正後の条件付き生存関数をグラフ化してみます。言い換えると、打ち切り後の生存関数をグラフ化してみます。

以下、コードです。

# 打ち切り後の未来
## 特定の継続顧客の生存関数のグラフ化
customer = 6
pred_survival_new_remain[customer].plot(label="pred_survival_new")

 

以下、実行結果です。

 

打ち切り後の離反時期を推定してみます。平均値ではなく中央値を使います。50%が離反する時期です。

以下、コードです。

# 打ち切り後の未来
## 推定結果（中央値）
cph.predict_median(
    customers_data,
    conditional_after=customers_data['tenure']
)

 

以下、実行結果です。

 

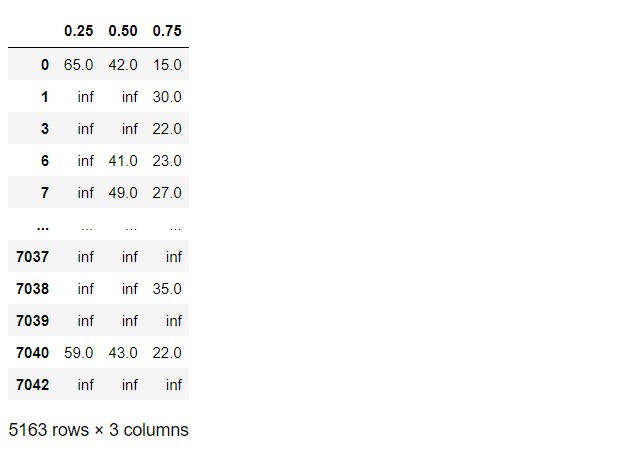
四分位を推定してみます。以下、コードです。

# 打ち切り後の未来
## 推定結果（第1四分位数，中央値（第2四分位数），第3四分位数）
cph.predict_percentile(
    customers_data,
    p=[0.25,0.5,0.75],
    conditional_after=customers_data['tenure']
)

 

以下、実行結果です。

 

まとめ

今回は、通信会社の顧客離反の事例データを使い、離反時期の予測の仕方を説明しました。

分類問題系の数理モデルを使った分析と比べると、生存時間分析は分かりにくく難しく感じる面もありますが、時系列に生存確率が減少（顧客である確率の減少）などが出力され、こちらの方がリアルで情報量も多いかと思います。

中央値を1つの基準として考えていますが、例えばどの時期に急激に生存率が急降下するのかなどを分析するのも良いでしょう。

今回は、LassoなCox比例ハザード回帰モデルを利用しましたが、特徴量（説明変数X）が可変なCox比例ハザードモデルや、ランダムフォレストを活用したランダム生存時間フォレスト（Random Survival Forest）ありますので、別の機会にお話しします。

【生存時間分析による離反時期分析 その3】Python の生存時間分析ライブラリー Lifelinesで予測した「離反時期（顧客であるまでの期間）」の精度検証