
データを集めたら、次にデータを分析しなければなりません。
集めたデータと分析の関係は、食材と料理の関係に似ています。良い食材であっても料理人の腕に問題があると台無しになることがあります。不十分な食材でも調理しだいで美味しくなることもあります。
データの分析の考え方と最も基本的な手法について、全15回にわたってお話しいたします。
- その1 定量分析と定性分析
- その2 分析の基本は比較
- その3 古くて新しいQC7つ道具 ※5回に分けてお話し
- その3-1 QC7つ道具の概要
- その3-2 ヒストグラム・管理図・散布図 ⇒ 今回
- その3-3 散布図+α(相関・回帰線)の話題
- その3-4 パレート図・特性要因図
- その3-5 チェックシート・層別
- その4 古くて新しい新QC7つ道具 ※5回に分けてお話し
- その5 要因分析と統計的因果推論 ※3回に分けてお話し
前回は、その3の「古くて新しいQC7つ道具」のその3-1の「QC7つ道具の概要」についてお話ししました。
今回は、その3-2の「ヒストグラム・管理図・散布図」です。
ヒストグラム
ヒストグラムとは横軸に階級、縦軸に度数をとった縦棒グラフで、データの分布を視覚的に捉えることができます。売上や受注金額など定量データを手にしたとき、「データの特徴を見よう!」ということで使います。
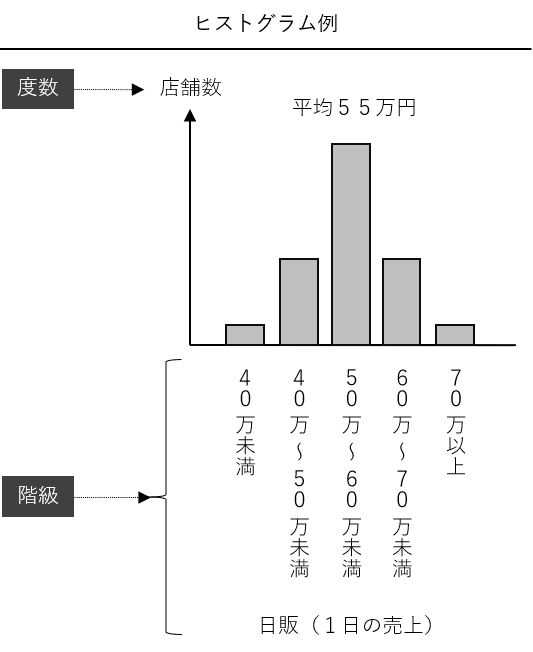
ヒストグラムを描くとき、併せて平均値や標準偏差(もしくは分散、分散は標準偏差を2乗したもの)、最大値、最小値などの統計学的な指標を計算します。
たまに、いきなり平均値だけで語る人がいます。平均値が同じでもヒストグラムの形が異なることは多々あります。解釈を間違う危険がありますので、可能な限りヒストグラムを描き分布の形を確認することをお薦めします。
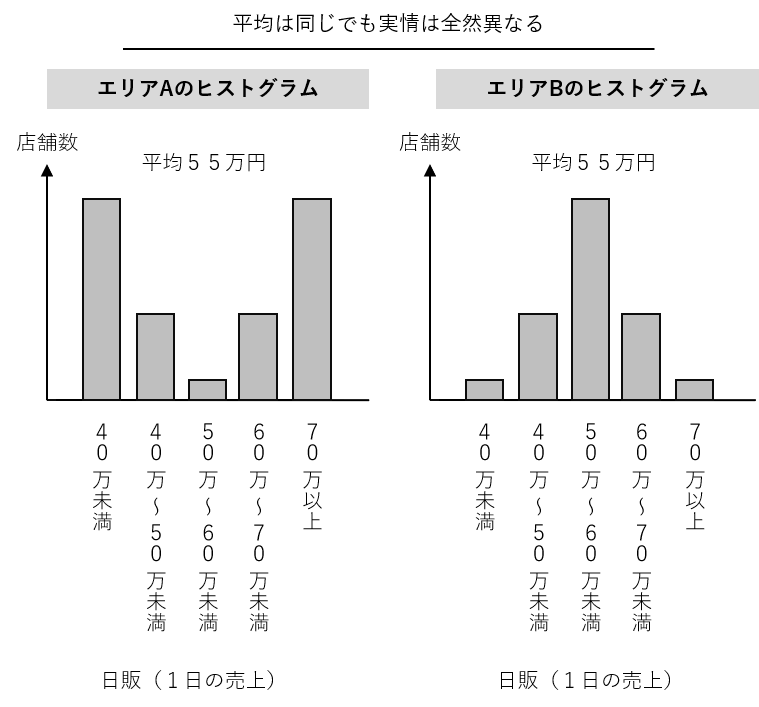
管理図
管理図とは、ひと言で言うと時系列の折れ線グラフです。売上や受注件数などの重要な指標の推移などをモニタリングするために利用します。
通常は、上方管理限界線と下方管理限界線という閾値を設け、その間の外にでたとき異常値と見なします。

例えば、日販(日単位の売上)をモニタリングしていたとします。
管理図上の異常値は、日販でヒストグラムを作ったとき、上方管理限界線を越えたデータはヒストグラムの右に、下方管理限界線を下まわったデータはヒストグラムの左に極端に現れます。
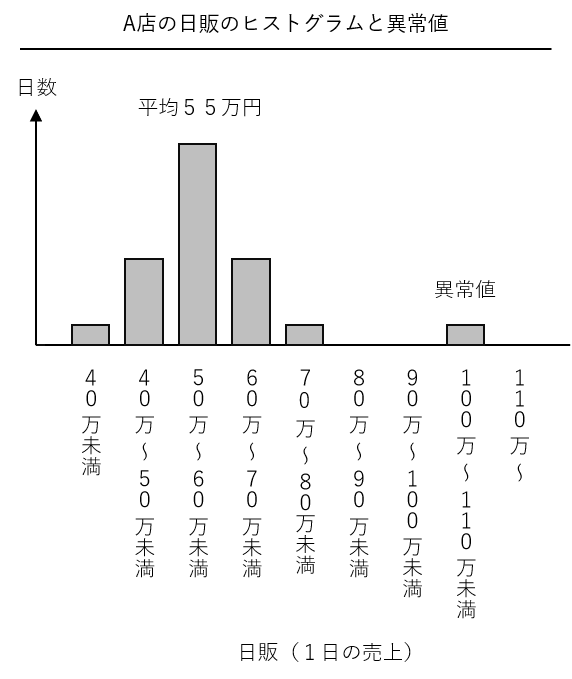
異常検知は、管理図を使うことでもできすし、ヒストグラムを使うことでもできます。日販の例のように時系列で推移するデータでない場合には、ヒストグラムを使い異常検知をすることになることでしょう。
散布図
ヒストグラムと管理図は、売上や受注金額などの1つの定量データの特徴を把握するものでした。1つの定量データの特徴を把握したら、定量データ間の関係性が気になります。
例えば……
- 客単価の高い店舗は、来店客数も多いのだろうか?
- 来店客数と関係があるのは、何であろうか?
……という感じです。
客単価の店舗は来店客数も多いのかもしれませんし、そうでないかもしれません。来店客数に影響するのは、降水量かもしれませんし、新聞の折り込みチラシの量かもしれません。
このように、散布図は2つの定量データの関係を把握するときに利用します。
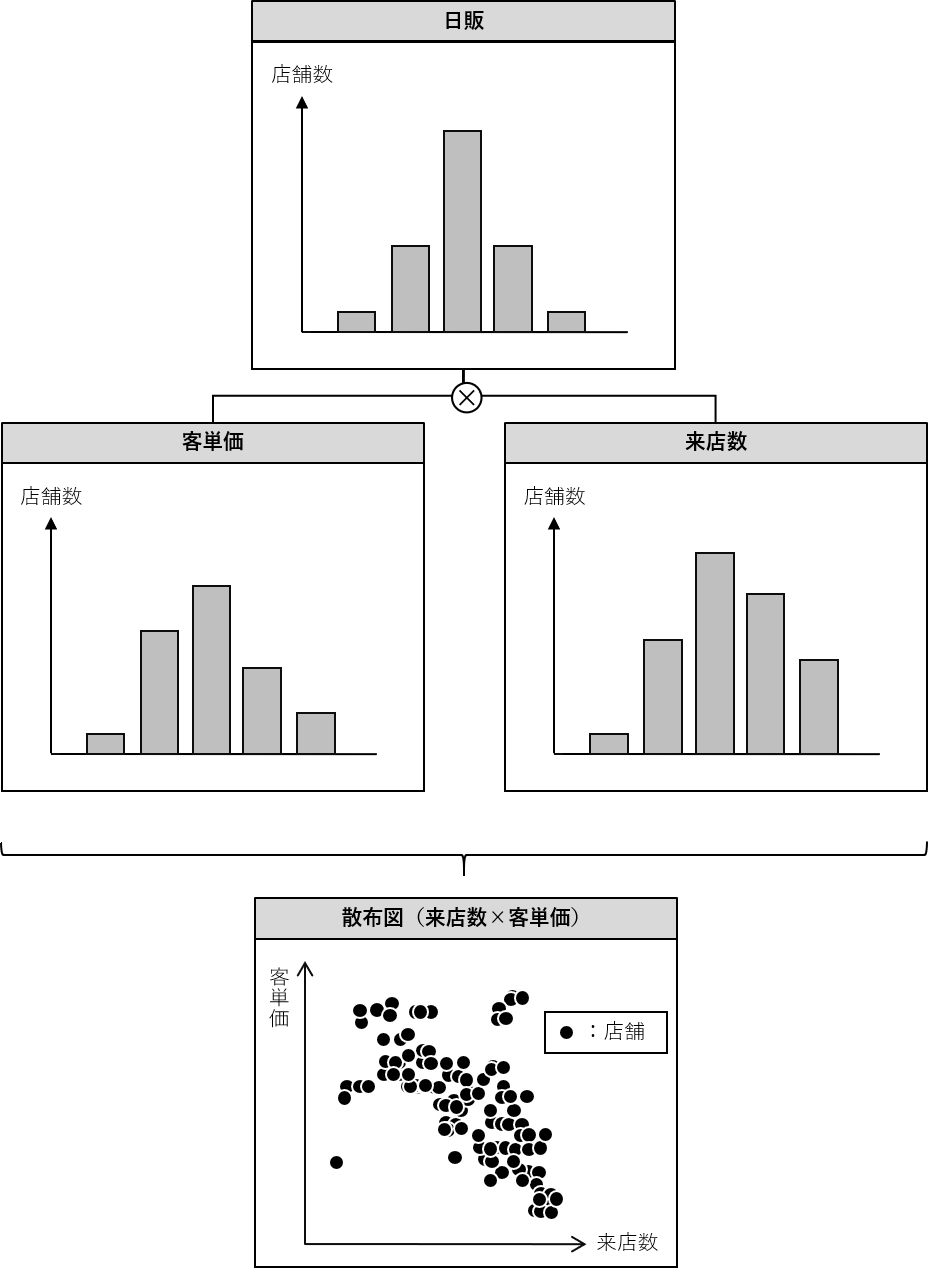
要は、先ず、ヒストグラムや管理図などで1つの定量データの特徴を把握し、その後、散布図で2つの定量データの関係を把握するという使い方をよくします。
相関係数
散布図を描くとき、併せて相関係数などの統計学的な指標を計算します。
相関係数は-1から+1の間の数値をとり……
- +1に近いほど「正の相関関係がある」(一方が増加すると他方も増加する傾向にある場合)
- -1に近いほど「負の相関関係がある」(一方が増加しているにもかかわらず他方が減少する傾向にある場合)
- 0は無相関(正の相関関係も負の相関関係もない)
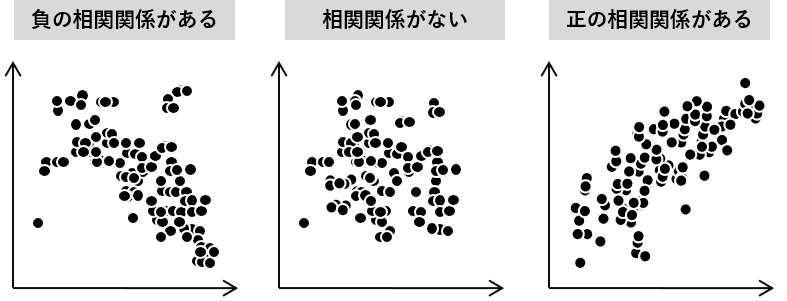
相関関係は、あくまでもデータ上の関係(厳密には線形的な関係)で、このような関係性が本当にあるのかは分かりませんし、そもそも因果関係ではありません。データからこのような関係が読み取れるということに過ぎません。
そのため、現場に詳しい人などと一緒に、散布図や相関係数などを眺めながら、どのようなことが言えそうなのかを議論する必要がでてきます。議論の結果、現実に起こっている現象がデータに現れたものなのか、因果関係と言っても差し支えないものなのかが、見えてきます。もし、現実世界を反映したものなのであれば、その現実世界の一部をデータで表現できたことになります。

このように、散布図や相関係数などの2つ(もしくは、2つ以上)のデータの関係性を分析する手法を使い、要因分析を実施することがあります。
要因分析を実施することで、例えば……
- 〇〇というアクションをしたら〇〇という結果になった
- 〇〇が起きると〇〇という結果になる
……とか、因果関係のようなものを考えていきます。
先ほど相関係数のところでお話ししたように、データだけで行う分析からは因果関係かどうかは分かりません。因果関係どころか、そのような現象が本当に起こっているのかどう怪しいものです。
50m走のタイムが遅いほど年収が高い
例えば、年収と50m走のタイムは正の相関があると言われています。50m走のタイムが遅いほど年収が高いのです。明らかに違和感があります。
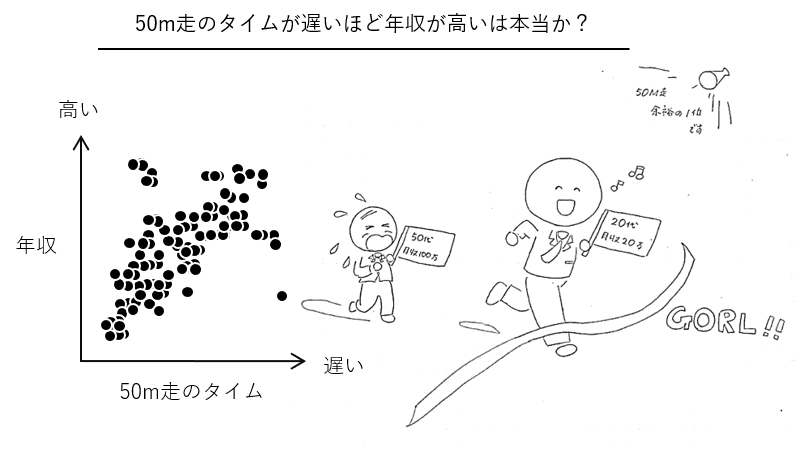
実は、年収と年齢が正の相関(年齢が高いほど年収が多い)をしていて、さらに50m走と年齢が正の相関(年齢が高いほど50m走のタイムが遅い)をしているがために、年収と50m走のタイムに正の相関があるのです。
このようなことはよくあります。データだけからは見えてきません。現場の人なら一発で見破れるケースが多いです。
データの特徴理解のために利用
ここまで説明したヒストグラムや管理図、散布図を、何気なく作成し使っている方も多いと思います。データそのものの特徴理解のために使ったりします。
やっていることは、データをグラフで視覚化し眺めているだけです。このようにデータを目で見て確かめることは、データ分析の基本となります。実際、単なるグラフでも意図をもって見ることが重要で、想像以上に得られる情報は多いです。

例えば.……
- 手元にあるデータに異常値がないかなとヒストグラムや管理図でデータを眺めたり、ある2つのデータの間に関連性はないだろうかと散布図で眺めたりします
- 異常値があれば、データの入力ミスなのか、それとも異常値が起こるような特別な何かが起こったのかなどを考え、データを整備したり異常の起こった原因を追究したりするきっかけになります
- 2つのデータの間に関連性があるのなら、その関係性は本当にあるのか現場に協力を仰ぎ調べたり、その関係性を使い有効な施策を打てるのであれば活用したりすることなどができます

要するに、高度な分析技術や数理モデル(予測モデルや異常検知モデルなど)ではなく、このような単純なグラフだけで、十分なデータ分析・活用が実現することもあります。あなどれません。実際、簡単なモニタリングや異常検知、要因分析などを実施することが可能です。
次回

今回は、その3の「古くて新しいQC7つ道具」のその3-2の「ヒストグラム・管理図・散布図」のお話しをしました。
- その1 定量分析と定性分析
- その2 分析の基本は比較
- その3 古くて新しいQC7つ道具 ※5回に分けてお話し
- その3-1 QC7つ道具の概要
- その3-2 ヒストグラム・管理図・散布図
- その3-3 散布図+α(相関・回帰線)の話題 ⇒ 次回
- その3-4 パレート図・特性要因図
- その3-5 チェックシート・層別
- その4 古くて新しい新QC7つ道具 ※5回に分けてお話し
- その5 要因分析と統計的因果推論 ※3回に分けてお話し
次回は、その3-3の「散布図+α(相関・回帰線)の話題」です。
もっと知りたい方はこちら
 |
14のフレームワークで考える かんき出版 (2014/9/18) |

