[For beginners] がんばれデータサイエンティスト！

分類問題のデータ不均衡を解消するSMOTE（Python版）<br>－ その2：基本的なSMOTEを活用した3つのケーススタディ －

分類問題のデータ不均衡を解消するSMOTE（Python版）
－ その2：基本的なSMOTEを活用した3つのケーススタディ －

データサイエンスの進化に伴い、多くの業界で複雑なデータ問題に直面しています。 特に、データ不均衡は分析精度の低下を引き起こし、有意義な洞察の抽出を困難にしています。 前回、データ不均衡問題を解消するための強力なテクニック...
分類問題のデータ不均衡を解消するSMOTE（Python版）<br>－ その1：SMOTEの基礎と imbalanced-learn の使い方 －

分類問題のデータ不均衡を解消するSMOTE（Python版）
－ その1：SMOTEの基礎と imbalanced-learn の使い方 －

データサイエンスの世界では、正確な分析と予測が成功の鍵となります。 しかし、多くの実際のデータセットは不均衡であり、これが特に分類問題において大きな課題となることがあります。 今回は、データ不均衡問題を解消するための強力...
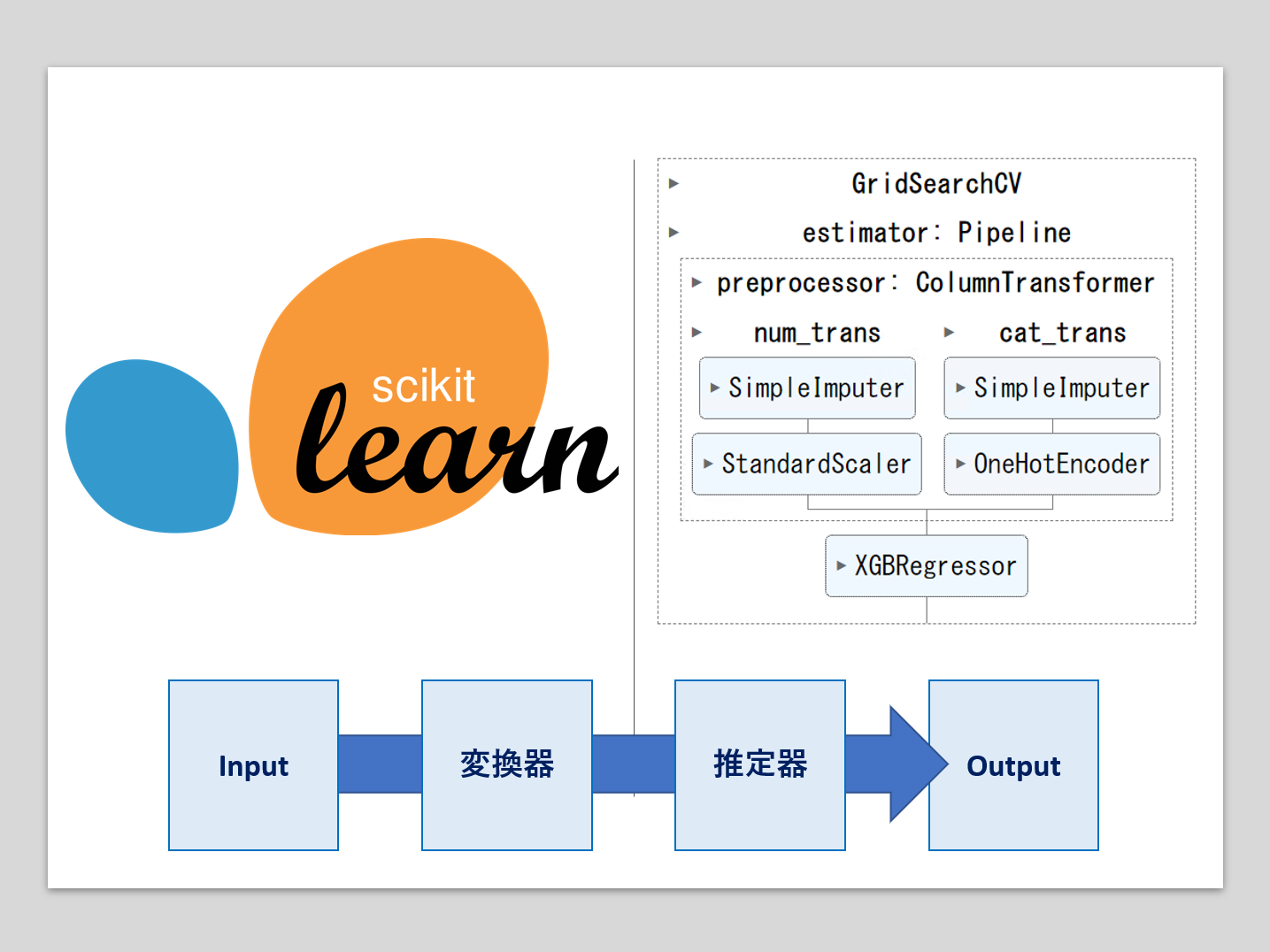
scikit-learnの機械学習パイプライン入門<br>（その4：変数ごとに変換器の処理を変える）

scikit-learnの機械学習パイプライン入門
（その4：変数ごとに変換器の処理を変える）

機械学習のパイプラインとは、複数の処理を直列に連結したものです。 最小構成は、1つの変換器と1つの推定器（予測器）を連結したものです。 変換器：特徴量X（説明変数）などの欠測値処理や変数変換などの、特徴量変換（Trans...
深層学習によるビジネス時系列分析ツール NeuralForecast（3）<br>– 時系列回帰モデルを深層学習で構築する方法 –

深層学習によるビジネス時系列分析ツール NeuralForecast（3）
– 時系列回帰モデルを深層学習で構築する方法 –

時系列予測モデルの、予測精度を向上させるために、外生変数（説明変数・特徴量）を利用することがあります。 例えば、需要予測のための価格や将来のプロモーション変数、電力負荷予測のための天気データなどです。 時系列データには、...
Python SciPyで手を動かしながら学ぶ数理最適化<br>– 第5回: Scikit-learnモデルとSciPy最適化の統合 –

Python SciPyで手を動かしながら学ぶ数理最適化
– 第5回: Scikit-learnモデルとSciPy最適化の統合 –

数理最適化と機械学習の融合は、ビジネスの意思決定に革命をもたらす可能性を秘めています。 具体的には、Scikit-learnで数理モデルを構築し、その数理モデルを目的変数としたSciPyを用い最適化問題を解きます。 例え...