第210話｜機械学習ABテスト – セールスアナリティクス

最もシンプルなデータ活用の1つがABテストです。

A案とB案のどちらがいいのかをデータで判断する、という感じのデータ分析・活用（データサイエンス実践）です。

この地味な、データ分析・活用（データサイエンス実践）は、明日からでも使えるものです。

古くは実験計画法・分散分析として、統計学的なメソッドの1つとして名を馳せていました。

今では、デジタルマーケティングの世界の必須メソッドの1つです。

統計学的な手法を用いるABテストですが、最近では機械学習的な手法を活用することも増えています。

今回は、「機械学習ABテスト」というお話しをします。

Contents

ABテストとは？
従来の統計的アプローチ「2標本検定」
統計的アプローチの限界
3つの数理モデル（アルゴリズム）
2標本検定（例：zスコア、t検定）の場合
線形回帰
決定木（ディシジョンツリー）
XGBoostやLightGBMなど
使い分け例
今回のまとめ

ABテストとは？

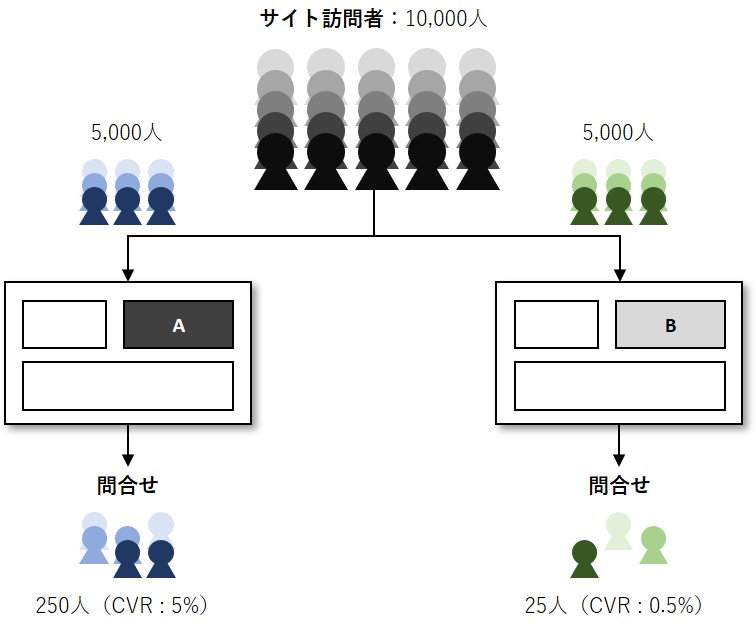
デジタルマーケティングの世界では、例えば……

ランディングページ
フォーム
タイトル

……などを決めるときに活用したりします。

あらかじめA案とB案を考えておき、どちらがいいのかをデータで判断します。

ABテストを拡張したものが多変量テストです。

デジタルマーケティングではなく別の領域では、実験計画法・分散分析・多重比較・コンジョイント分析などと呼ばれていたものです。

従来の統計的アプローチ「2標本検定」

従来の実験計画法・分散分析・多重比較・コンジョイント分析などでは、主に統計学的なアプローチを用います。

ABテストも同様です。

2標本検定（例：zスコア、t検定）という統計的な手法を使うことが多いです。2標本検定（例：zスコア、t検定）とは、2つの母集団（処理群と対照群）の平均などの差を検定することです。

対照群：比較の基準となるグループ（母集団）・・・例えば、A群（A案と接触したユーザ）
処理群：処理を加えたグループ（母集団）・・・例えば、B群（B案と接触したユーザ）

例えば、元のランディングページを見せるサイト訪問者を「対照群」、新しいランディングページを見せるサイト訪問者を「処理群」、処理群と対照群を比べて問い合わせや購入などの割合であるCVR（コンバージョンレート）が異なるかどうかを検討します。

2つの母集団（処理群と対照群）と、難しそうな用語を使いましたが、要は2つのグループ（A群とB群）を比較し検討するということです。

統計的アプローチの限界

2つの母集団（A群とB群）を比較するとき、あるポイントに絞って単純化して比較しています。

しかし、現実世界は複雑です。

例えば、ランディングページに訪問者の背景（性年代・趣味・価値観など）は異なりますし、ランディングページに滞在する時間も異なります。

3つの数理モデル（アルゴリズム）

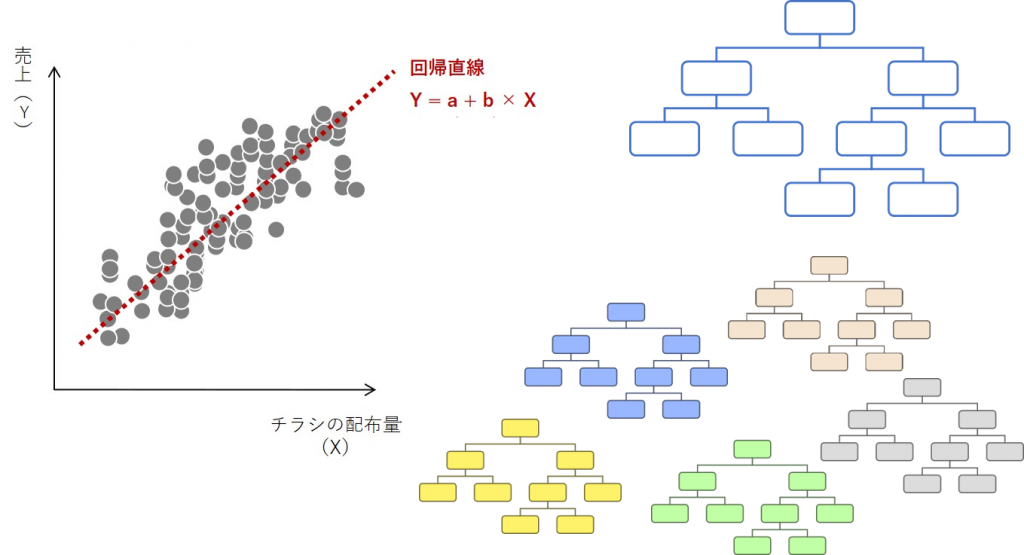
2標本検定（例：zスコア、t検定）による統計的アプローチによるABテストは、今でも有効です。

2標本検定（例：zスコア、t検定）に次の3つの数理モデル（アルゴリズム）を付け加えると、より良くなります。

線形回帰：線形・解釈性大・複雑性低
決定木（ディシジョンツリー）：非線形・解釈性大・複雑性低
XGBoostやLightGBMなど：非線形・解釈性小・複雑性大

解釈性や複雑性は私の主観ですが、大きくは間違ってはいないかと思います。

ここで使っている解釈性とは、結果が解釈しやすく他者に説明のしやすさです。ここで使っている複雑性とは、どれだけ複雑な状況をモデル化できるかとというものです。

この3つの中では、「線形回帰」が最も簡単な数理モデル（アルゴリズム）で、「XGBoostやLightGBMなど」が最も難しい数理モデル（アルゴリズム）になります。

上から順番に実施していきます。簡単なものから始めるということです。

2標本検定（例：zスコア、t検定）の場合

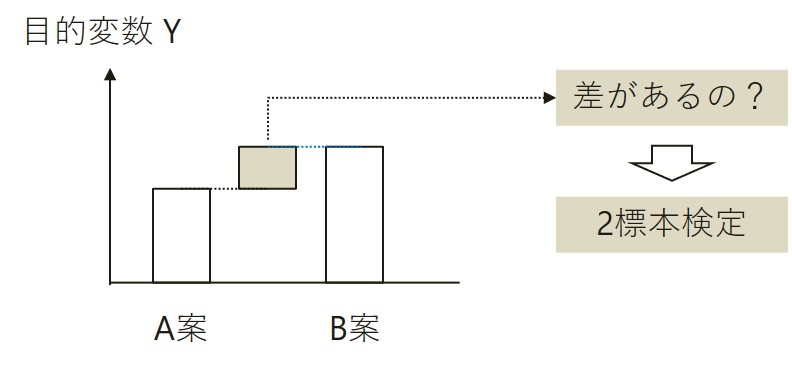
2標本検定（例：zスコア、t検定）の場合、A群とB群の目的変数Yを集計（平均値など）し比較するだけです。

目的変数Yとは、着目している指標で、問い合せ者数や購入者数、購入金額などです。

目的変数Yと一緒に登場するワードに、説明変数Xというものがあります。

説明変数Xとは、目的変数Yに影響を与えるであろう変数を指し、機械学習の世界では特徴量というワードで表現したりします。

この場合の説明変数Xは、どの群に所属するのか（A群 or B群）を表現する変数（ここでは、群変数と表現します）のみになります。

「線形回帰」で考えると、単回帰と呼ばれる数理モデルになります。

線形回帰

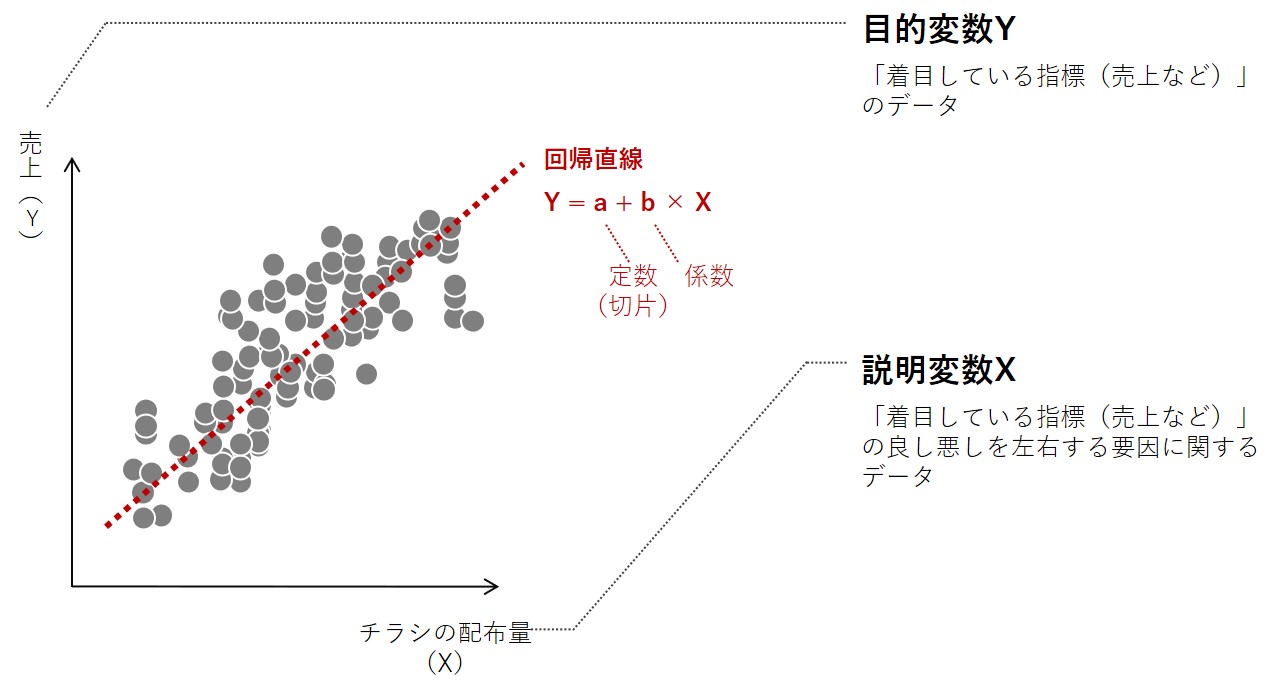
「線形回帰」でABテストを実施する場合、最も簡単なものは次のような設定です。

目的変数Y：着目している指標（問い合せ者数や購入者数、購入金額など）
説明変数X：群変数（どの群に所属するのかを表現する変数）

これでは、2標本検定（例：zスコア、t検定）と本質的に変わりません。

そこで、説明変数Xで扱う変数を増やします。重回帰と呼ばれる「線形回帰」の数理モデルです。

2標本検定（例：zスコア、t検定）の場合と異なり、群変数（A群 or B群）の影響を以外を分析対象にします。

「線形回帰」の結果、目的変数Yを左右しているであろう説明変数Xが分かります。

正直ここまででもいいかもしれません。やるべきことの方向性が見えてくるからです。

しかし、あくまでも直線的な線形の関係性しか分かりません。

より複雑な関係性（直線的な線形の関係性を超える関係性）を知ることで、何をすべきかがより具体的に分かりやすくなります。

例えば、「もし説明変数Xを〇〇だけ変化させると、そのとき目的変数Yは〇〇だけ変化する」という実行ルール（If-Thenルール）が欲しいところです。

If-Thenルールを抽出するための手法の1つが「決定木（ディシジョンツリー）」です。

決定木（ディシジョンツリー）

「線形回帰」の次に「決定木（ディシジョンツリー）」を実施します。

「決定木（ディシジョンツリー）」の目的変数Yと説明変数Xは、「線形回帰」と同じで構いません。

「決決定木（ディシジョンツリー）」を実行すると、If-Thenルールを表現するツリーが手に入ります。

このことから、「もし説明変数Xを〇〇だけ変化させると、そのとき目的変数Yは〇〇だけ変化する」という実行ルール（If-Thenルール）を得ることができ、目的変数Yををより良くするために何をすべきかが見えてきます。

「線形回帰」との大きな違いは、「決定木（ディシジョンツリー）」の場合には説明変数Xをどうすべきかが組み合わせで分かることです。

線形回帰の場合例：「説明変数X1」と「説明変数X2」をより大きくすると目的変数Yがより良くなる
決定木（ディシジョンツリー）の場合例：「0<説明変数X1≦100」かつ「500≦説明変数X2」にすると目的変数Yがより良くなる

何をすべきかが分かることは非常に大きいです。

どうせなら、未来を高精度で予測したいものです。

XGBoostやLightGBMなど

木（ツリー）が、たくさんあると森（フォレスト）になります。

「決定木（ディシジョンツリー）」を、たくさん作って予測に活かそうという数理モデル（アルゴリズム）が、ランダムフォレストという数理モデル（アルゴリズム）です。

ランダムフォレストを発展させたのが「XGBoost」で、「XGBoost」を発展させたのが「LightGBM」です。

どれを使ってもいいですが、「XGBoost」ぐらいがちょうどいいかもしれません。

現実的には「XGBoost」を解釈し実行ルール（If-Thenルール）を見出すのは至難の業です。

ただ、「線形回帰」や「決定木（ディシジョンツリー）」に比べ、予測精度が高いです。

目的変数Yと説明変数Xの複雑な関係性をモデル化しているからです。

一様、「XGBoost」などにも、特徴量重要度（Feature Importance）や、SHAP(SHapley Additive exPlanation) などの予測貢献度などと呼ばれる指標を出すことが出来ますが、実行ルール（If-Thenルール）という感じではありませんし、まだまだ発展途上の分野です。