所得分布の不均衡を研究したヴィルフレド・パレート(Vilfredo Pareto)から名付けられた、パレートの法則(20:80の法則もしくは80:20の法則)と呼ばれるものがあります。
この法則は……
- 売上上位20%の商品が、売上全体の80%を占める
- 取引額上位20%の顧客が、売上全体の80%をもたらす
- 20%の顧客からのクレーム対応に、80%の時間を費やす
……というものです。
実際は、10:90であったり30:70であったり、10:50であったり1:90であったりします。
元々は……
人口の20%によって富の80%が支配される
……というものでした。
今回は、「パレート指数による売上分析」というお話しをします。
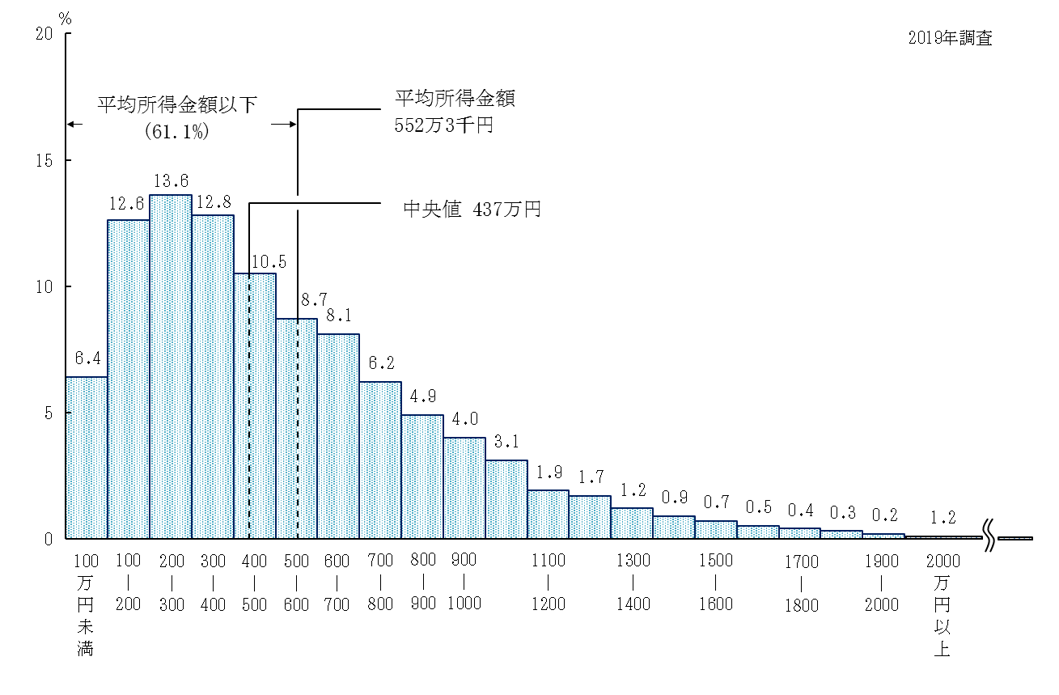
日本の所得分布
日本の所得分布です。
https://www.mhlw.go.jp/toukei/saikin/hw/k-tyosa/k-tyosa19/index.html
平均値が522万3千円で、中央値が437万円です。平均値である522万3千円以下の世帯が61.1%(平均以下の世帯の割合)です。
ある集団のデータを小さい順に並べたときに、中央に位置する値を「中央値」と言います。
通常パレート分布に従うとき、平均値は中央値よりも高くなります。なぜならば、極端に所得の大きな集団に平均値が押し上げられるからです。
要は、極端に所得の大きな人がいるどうかの影響を平均値は受けます。中央値は、そのような影響を受けにくいです。
パレート分布
パレート分布というものがあります。
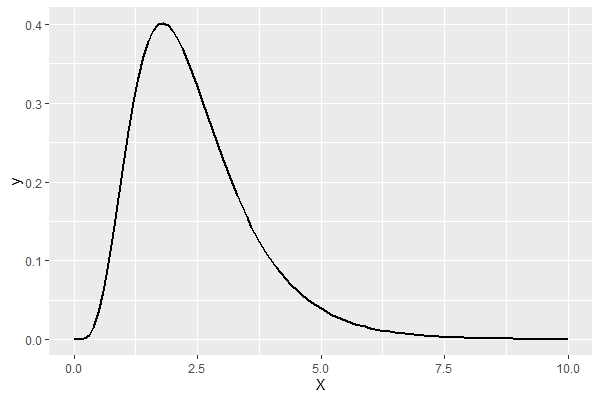
数理統計学で登場する正規分布やポアソン分布、2項分布などと同じ確率分布の1つです。
このパレート分布を、パレートの第1法則と言い、所得分布を表現するときに利用します。
パレート分布そのものも進化(???)を遂げており、一般化パレート分布(generalized Pareto distribution)や指数化パレート分布(exponentiated Pareto distribution)、指数一般化パレート分布(exponentiated generalized Pareto distribution)などがあります。
パレートの法則が有効なケースの場合、このパレート分布を利用した方がいいでしょう。
パレートの法則が有効なケースとは、先ほどの所得のように、極端に所得の大きな人がいる場合に有効です。
パレート指数
例えば、10:90なのか、20:80なのか、30:70なのか、10:50なのか、1:90なのかでパレート分布の形状は異なることでしょう。
パレート分布のパラメータを変えることで、色々なパレート分布を表現することができます。一般的には3つのパラメータ(もしくは2つ)があります。このパレート分布のパラメータの1つが、パレート指数と呼ばれています。
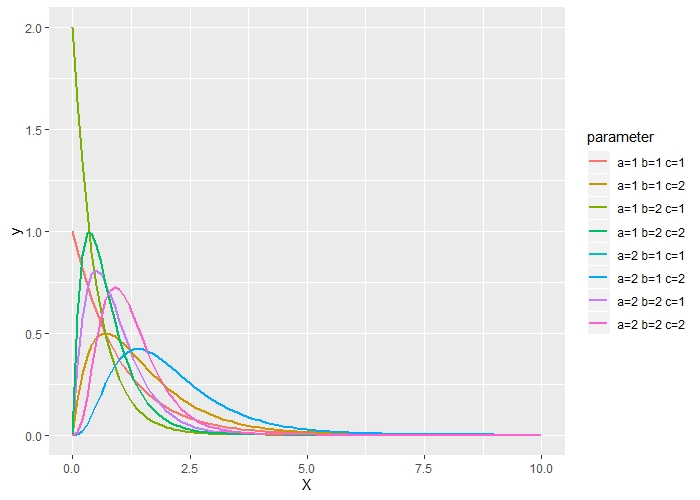
パレート指数などのパラメータに対し、色々な分析がなされています。
例えば、経済成長や所得格差などの関係性の分析や、ロングテール理論との関係性などです。
有名なパレート指数による経済格差の分析例

- パレート指数が小さいとき、所得の大きい人と小さい人の格差が大きくなります。逆もしかりです
- パレート指数が大きいとき、所得の大きい人と小さい人の格差が小さくなります。逆もしかりです
例えば、パレート指数の増大は、上位所得者の減少や下位所得者の増加を意味します。

所得格差が小さくなるとも言えるし、貧しい生活を強いられる人が増えたとも言えます。
日本社会が、バブル崩壊前後で、パレート指数が大きく変化したという研究などもあります。
ビジネスはパレートな世界
最初に述べましたが、この法則は……
- 売上上位20%の商品が、売上全体の80%を占める
- 取引額上位20%の顧客が、売上全体の80%をもたらす
- 20%の顧客からのクレーム対応に、80%の時間を費やす
……というものです。
実際は、10:90であったり30:70であったり、10:50であったり1:90であったりします。

ビジネスはパレートな世界の住人でしょう。
例えば……
- チェーン店であれば、極端に売上の大きい店舗はあります
- 営業パーソンであれば、極端に受注額の大きい人はいます
- 顧客であれば、極端に取引額の大きい得意先はあります
- 商品であれば、極端に利益額の大きい商品はあります
- 日販であれば、極端に売上高の高い日はあります
……などなど。
パレート図と累積比率マップ
パレートの法則と言えば、パレート図です。
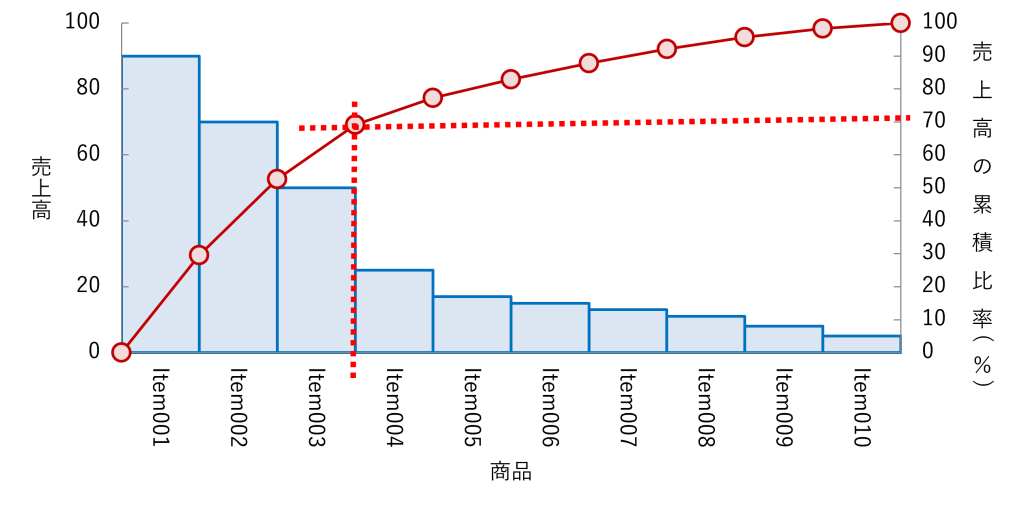
売上の大きな商品をから順番に左から並べています。左のタテ軸のメモリが売上高、右のタテ軸が売上高の累積比率になります。
今度は売上の小さな商品をから順番に並べ2つの累積比率を求め、別のマップを作ってみます。
- 商品Itemの累積比率(%)
- 売上高の累積比率(%)
ヨコ軸に商品Itemの累積比率(%)、タテ軸に売上高の累積比率(%)にしたのが、以下の累積比率マップです。
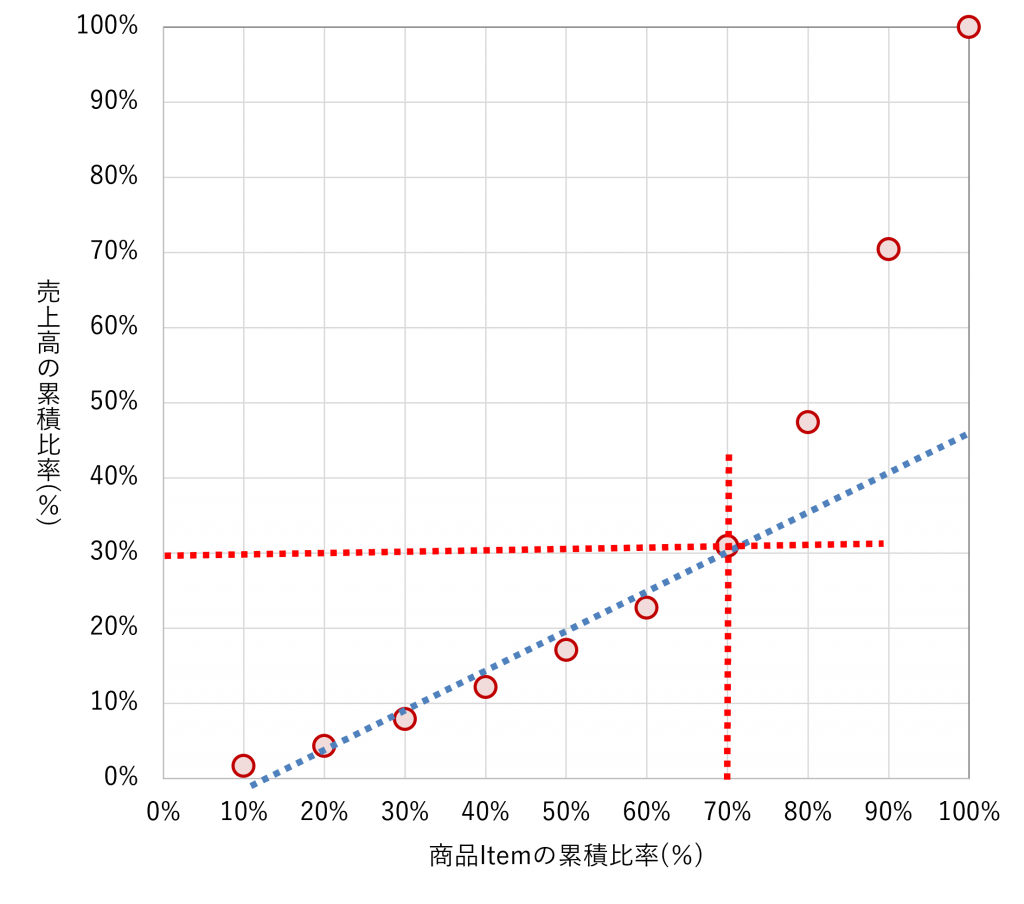
直線で近似すると、急に大きく外れる(もしくは、傾きの異なる直線になる)ポイントがあります。
この例では……
- 商品Itemの累積比率(%):70%
- 売上高の累積比率(%):30%
……になっています。
下位70%の商品で売上の30%を占めている(上位30%の商品で売上の70%を占めている)ということになります。
今回の例のように、30:70となるわけではなく、20:50とか、1:90とかもあります。
今回は、傾きの異なる直線になるポイントが1つでしたが、2つ3つになることもあります。そのポイントで商品のグルーピングを行えば、売れ筋商品、通常商品などに分類することができます。
パレート指数を分析しよう
先ほど、パレート指数などのパラメータに対し、色々な分析がなされていると言いました。
例えば、経済成長や所得格差などの関係性の分析や、ロングテール理論との関係性などです。

あなたの担当しているビジネスや業務に当てはめてみてもいいでしょう。
その中で、売上分析などはもってこいです。
今あるデータに対し、パレート分布を推定し、パレート指数などのパラメータの変化を眺めてみてもいいですし、パレート指数などのパラメータに対し何が関係しているのかを分析してもいいでしょう。
今回のまとめ
今回は、「パレート指数による売上分析」というお話しをしました。
この法則は……
- 売上上位20%の商品が、売上全体の80%を占める
- 取引額上位20%の顧客が、売上全体の80%をもたらす
- 20%の顧客からのクレーム対応に、80%の時間を費やす
……というものです。
実際は、10:90であったり30:70であったり、10:50であったり1:90であったりします。
元々は……
人口の20%によって富の80%が支配される
……というものでした。
ビジネスはパレートな世界の住人でしょう。
例えば……
- チェーン店であれば、極端に売上の大きい店舗はあります
- 営業パーソンであれば、極端に受注額の大きい人はいます
- 顧客であれば、極端に取引額の大きい得意先はあります
- 商品であれば、極端に利益額の大きい商品はあります
- 日販であれば、極端に売上高の高い日はあります
……などなど。
どのようにして、得られたデータからパレート分布を推定するのかは、別の機会(「[For beginners] がんばれデータサイエンティスト!」の「Rで推定するパレート分布」)でお話しします。